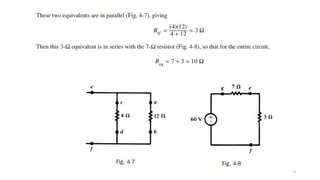
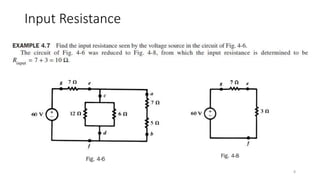
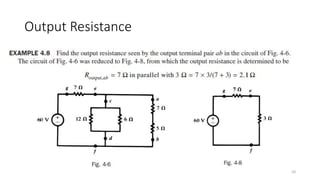
The document outlines various network analysis techniques, including network reduction, input resistance, output resistance, and the superposition principle. Network reduction simplifies circuit analysis by determining equivalent resistances through series and parallel combinations, while input and output resistances affect voltages in passive networks. The superposition principle allows for the analysis of linear networks with multiple independent sources by evaluating their effects individually, but it cannot be used to calculate power due to the nonlinear relationship with current and voltage.

1. Network Analysis Techniques
Network Reduction
Input Resistance
Superposition
1

2. Network Reduction
• The equivalent resistance of series and parallel branches, combined
with the voltage and current division rules, provides another method
of analyzing a network.
• This method is tedious and usually requires the drawing of several
additional circuits.
• Even so, the process of reducing the network provides a very clear
picture of the overall functioning of the network in terms of voltages,
currents, and power.
• The reduction begins with a scan of the network to pick out series
and parallel combinations of resistors.
2

3. Network Reduction
3

4. 4

5. 5

6. 6

7. Input Resistance
7

8. Input Resistance
8

9. Output Resistance
• A voltage source applied to a passive network results in voltages
between all nodes of the network.
• An external resistor connected between two nodes will draw current
from the network and in general will reduce the voltage between
those nodes.
• This is due to the voltage across the output resistance (see the
Thévenin equivalent circuit).
• The output resistance is found by dividing the open-circuited voltage
to the short-circuited current between the desired terminals.
9

10. Output Resistance
10

11. Superposition
• A linear network which contains two or more independent sources can be
analyzed to obtain the various voltages and branch currents by allowing
the sources to act one at a time, then superposing the results.
• This principle applies because of the linear relationship between current
and voltage.
• With dependent sources, superposition can be used only when the control
functions are external to the network containing the sources, so that the
controls are unchanged as the sources act one at a time.
• Voltage sources to be suppressed while a single source acts are replaced by
short circuits; current sources are replaced by open circuits.
• Superposition cannot be directly applied to the computation of power,
because power in an element is proportional to the square of the current
or the square of the voltage, which is a nonlinear relationship.
11

12. 12

13. 13