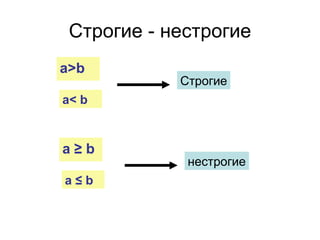
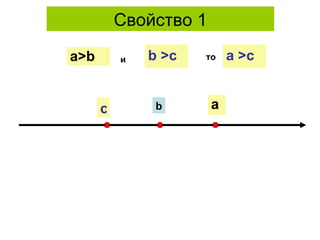
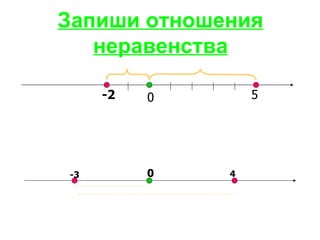
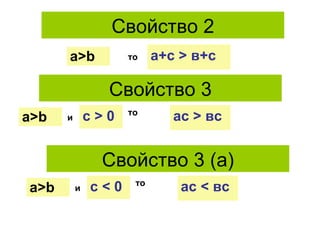
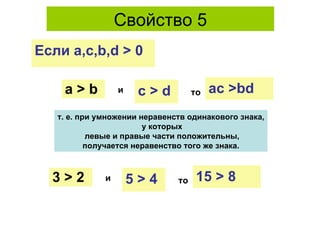
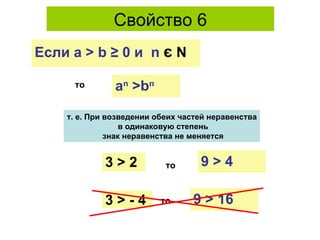
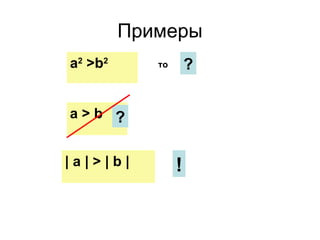
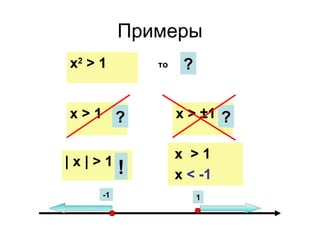
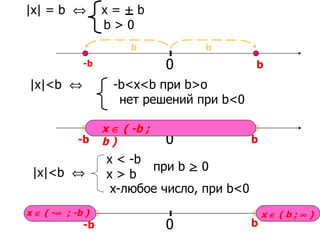
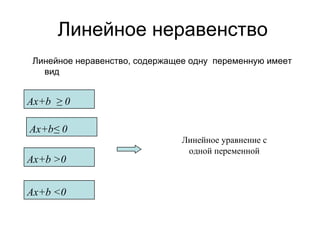
Документ рассматривает свойства неравенств, включая линейные, квадратичные и иррациональные неравенства с их решениями. Описаны различные свойства неравенств, таких как сложение и умножение, а также правила для строгих и нестрогих неравенств. Приведены примеры и задания для закрепления материала.

1. Неравества и их свойства Людмила Рождественская 2004 г.

2. План темы Свойства неравеств Линейные неравенства Квадратичные неравенства Решение неравенств высших степеней методом интервалов Дробно-рациональные неравенства Неравенства с модулем Иррациональные неравенства

3. Определение Говорят, что число a больше числа b и пишут a >b , если разность a-b положительна. Говорят, что число a меньше числа b и пишут a < b , если разность a-b отрицательна.

4. Строгие - нестрогие a >b a< b Строгие а ≥ b а ≤ b нестрогие

5. Свойство 1 a>b b >c и то а >c a b c

6. Запиши отношения неравенства 4 -3 0 0 -2 5

7. Свойство 2 a>b то а+с > в+ c Свойство 3 a>b то ас > в c и с > 0 Свойство 3 (а) a>b то ас < в c и с < 0

8. Свойство 4 a>b с >d и то a+c >b+d т. е. при сложении неравенств одинакового знака получается неравенство того же знака. 2 > 1 3 > -2 и то 5 > -1

9. Свойство 5 а > b с > d и то ac >bd т. е. при умножении неравенств одинакового знака, у которых левые и правые части положительны, получается неравенство того же знака. Если а, c , b , d > 0 3 > 2 5 > 4 и то 15 > 8

10. Свойство 6 то a n >b n т. е. При возведении обеих частей неравенства в одинаковую степень знак неравенства не меняется Если а > b ≥ 0 и n є N 3 > 2 то 9 > 4 3 > - 4 то 9 > 16

11. Свойство 7 то n √ a > n √ b т. е. При извлечении из обеих частей неравенства корня одной степени знак неравенства не меняется Если а > b ≥ 0 и n є N 3 > 2 то 9 > 4

12. Примеры a 2 >b 2 то ? a > b ? | a | > | b | !

13. Примеры х 2 > 1 то ? х > 1 ? | х | > 1 ! х > ± 1 ? х > 1 х < -1 1 -1

14. |x| = b  x = + b b > 0 0 b b b -b b -b |x|<b  -b<x<b при b>o нет решений при b<0 x < -b x > b при b > 0 x-любое число, при b<0 |x|<b  b -b 0 0 x  ( -b ; b ) x  ( -  ; -b ) x  ( b ;  )

15. Д/З § 3.5 № 385-391 (четные) § 3.6 № 398 - 400 (четные)

16. Линейное неравенство, содержащее одну переменную имеет вид Линейное неравенство Линейное уравнение с одной переменной Ax + b ≥ 0 Ax + b ≤ 0 Ax + b > 0 Ax + b < 0