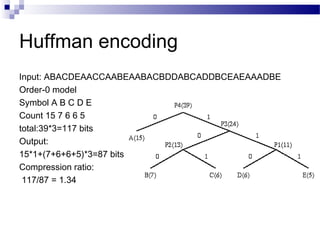
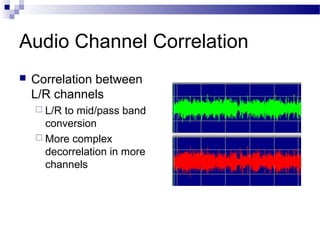
This document discusses multimedia compression. It begins by explaining why compression is needed due to the large size of raw audio and video data. It then outlines an overview of generic compression algorithms and content-specific compression techniques. It discusses lossy compression and introduces common lossless compression algorithms like Huffman coding and Arithmetic coding. Finally, it explains how content-specific compression aims to further reduce redundancy by de-correlating audio, images, and video based on properties like temporal, channel, color space, and spatial correlations.

1. Multimedia
Compression
BY
V.PRADEEPA
II – M.SC(CS&IT)
NADAR SARASWATHI
COLLEGE OF ARTS
AND SCIENCE, THENI

2. Why Compress
 Raw data are huge.
 Audio:
CD quality music
44.1kHz*16bit*2 channel=1.4Mbps
 Video:
near-DVD quality true color animation
640px*480px*30fps*24bit=220Mbps
 Impractical in storage and bandwidth

3. Outline
 Generic Compression Overview
 Content specific Compression
 Lossy Compression

4. Introduction to
Generic Compression
Algorithm
Lossless Compression

5. Generic Compression
 Also called Entropy Encoding
 Lossless Compression Algorithms
 Entropy can defined as:
 Need statistical knowledge of data
 Well-known Algorithms:
 Rice coding
 Huffman coding
 Arithmetic coding

6. Huffman encoding
Input: ABACDEAACCAABEAABACBDDABCADDBCEAEAAADBE
Order-0 model
Symbol A B C D E
Count 15 7 6 6 5
total:39*3=117 bits
Output:
15*1+(7+6+6+5)*3=87 bits
Compression ratio:
117/87 = 1.34

7. Property of Huffman encoding
 Easy to implement, high encoding speed
 Unique Prefix Property: no code is a
prefix to any other code
 Adaptive Huffman encoding:
statistical knowledge not available
update Huffman tree when needed

8. Arithmetic Encoding
 Symbol X, Y
prob(X) = 2/3
prob(Y) = 1/3

9. Property of Arithmetic Encoding
 Prevent entropy wasting in Huffman
coding, for the number of bits to represent
a symbol can be non-integer
 About 5~10% smaller than Huffman
coding
 Computational intensive
 US patented!!
 Both Huffman and Arithmetic are used in
the entropy encoding stage in JPEG

10. Application of General
Compression
 Generic file compression like Zip, Rar,
gzip, bzip, etc.
 Final stage of content specific
compression
JPEG uses Huffman or Arithmetic
Monkey’s Audio (ape) uses Rice
Lossless Audio (La) uses Arithmetic

11. Content specific
Compression
Further De-correlation

12. De-correlation
 Correlation means redundancy
 However, general algorithm may not find
content-specific correlation
 General algorithm of higher order may not be
efficient enough
 No matter lossy or lossless, multimedia file
format use content-specific pre-filter as 1st
step to
reduce data redundancy.

13. Correlation in Multimedia
 Audio:
Temporal, Channel
 Still Image:
Color space, Spatial, Stereo
 Video:
Temporal

14. Audio Channel Correlation
 Correlation between
L/R channels
 L/R to mid/pass band
conversion
 More complex
decorrelation in more
channels