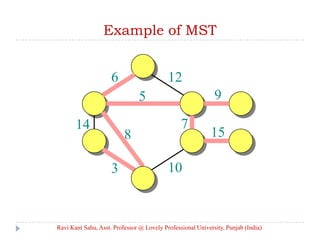
The document discusses minimum spanning trees (MST) in graph theory, detailing Prim's and Kruskal's algorithms for finding MSTs in connected, undirected graphs with distinct edge weights. Prim's algorithm uses a priority queue to maintain the minimum weight edges, while Kruskal's algorithm builds a forest and combines trees using a union-find structure. Both algorithms have a complexity of O(e log v).

1. Data Structures
Lecture 28: Minimum Spanning Tree

2. Outlines
 Minimum Spanning Tree
 Prim’s Algorithm
 Kruskal’s Algorithm
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

3. Minimum Spanning Tree
 Input: A connected, undirected graph G = (V, E)
with weight function w : E R.
• For simplicity, we assume that all edge weights are
distinct.
• Output: A spanning tree T, a tree that connects all
vertices, of minimum weight:
Tvu
vuwTw
),(
),()(
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

4. Example of MST
6 12
5
14
3
8
10
15
9
7
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

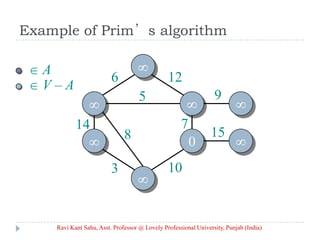
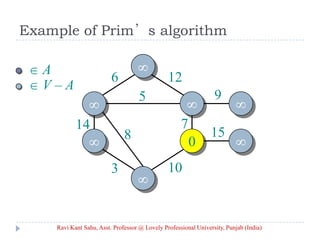
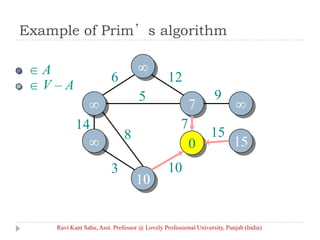
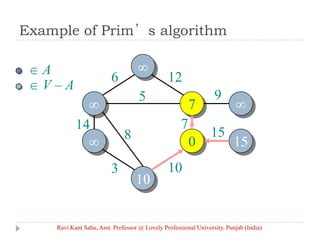
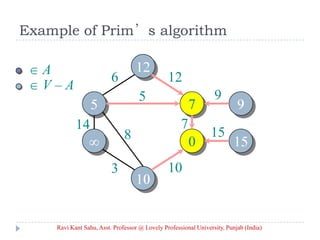
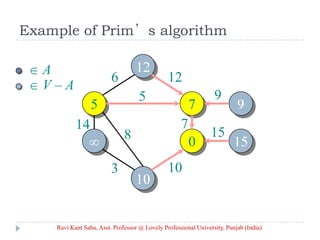
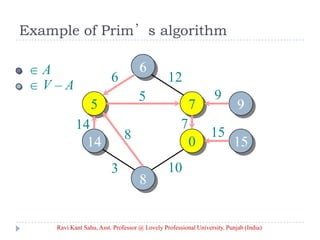
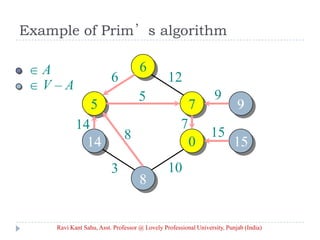
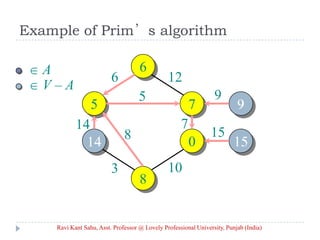
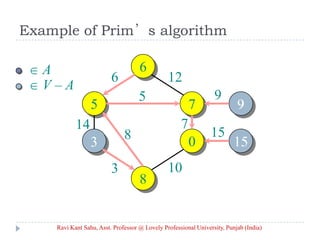
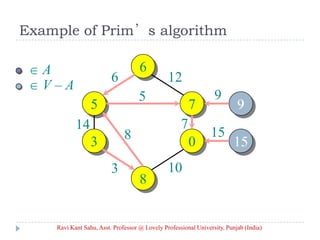
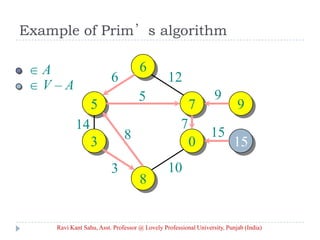
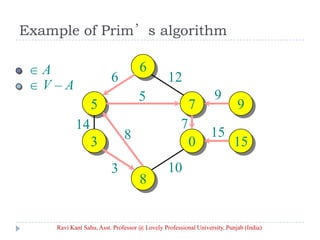
5. Prim’s Algorithm
IDEA: Maintain V – A as a priority queue Q. Key
each vertex in Q with the weight of the least-
weight edge connecting it to a vertex in A.
Q V
key[v] for all v V
key[s] 0 for some arbitrary s V
while Q
do u EXTRACT-MIN(Q)
for each v Adj[u]
do if v Q and w(u, v) < key[v]
then key[v] w(u, v) ⊳ DECREASE-KEY
[v] u
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

6. Example of Prim’s algorithm
A
V – A
0
6 12
5
14
3
8
10
15
9
7
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

7. Example of Prim’s algorithm
A
V – A
0
6 12
5
14
3
8
10
15
9
7
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

8. Example of Prim’s algorithm
A
V – A
0
6 12
5
14
3
8
10
15
9
7
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

9. Example of Prim’s algorithm
A
V – A
7
0
6 12
5
14
3
8
10
15
9
7
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

10. Example of Prim’s algorithm
A
V – A
7
0
6 12
5
14
3
8
10
15
9
7
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

11. Example of Prim’s algorithm
A
V – A
5 7
0
6 12
5
14
3
8
10
15
9
7
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

12. Example of Prim’s algorithm
A
V – A
5 7
0
6 12
5
14
3
8
10
15
9
7
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

13. Example of Prim’s algorithm
A
V – A
6
5 7
0
6 12
5
14
3
8
10
15
9
7
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

14. Example of Prim’s algorithm
A
V – A
6
5 7
0
8
6 12
5
14
3
8
10
15
9
7
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

15. Example of Prim’s algorithm
A
V – A
6
5 7
0
8
6 12
5
14
3
8
10
15
9
7
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

16. Example of Prim’s algorithm
A
V – A
6
5 7
3 0
8
6 12
5
14
3
8
10
15
9
7
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

17. Example of Prim’s algorithm
A
V – A
6
5 7
3 0
8
9
6 12
5
14
3
8
10
15
9
7
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

18. Example of Prim’s algorithm
A
V – A
6
5 7
3 0
8
9
15
6 12
5
14
3
8
10
15
9
7
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

19. Kruskal’s Algorithm
It is a greedy algorithm.
 In Kruskal’s algorithm, the set A is a forest.
 The safe edge is added to A is always a least-weight edge in the
graph that connects two distinct Components.
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

20. Kruskal’s Algorithm
 The operation FIND-SET(u) returns a representative element
from the set that contains u.
 Thus we can determine whether two vertices u and v belong to
the same tree by testing whether
FIND-SET(u) = FIND-SET(v)
 The combining of trees is accomplished by the
UNION procedure
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

21. Kruskal’s Algorithm
1. A
2. for each vertex v V[G]
3.do MAKE-SET(v)
4.short the edges of E into non-decreasing order
by weight.
5.for each edge (u, v) E, taken in non-decreasing order
by weight.
6.do if FIND-SET(u) != FIND-SET(v)
7. then, A  A U {(u, v)}
8. UNION(u, v)
9.return A
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

22. Complexity
Prim’s Algorithm: O(E logV)
Kruskal’s Algorithm: O(E logV)
Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)

23. Ravi Kant Sahu, Asst. Professor @ Lovely Professional University, Punjab (India)