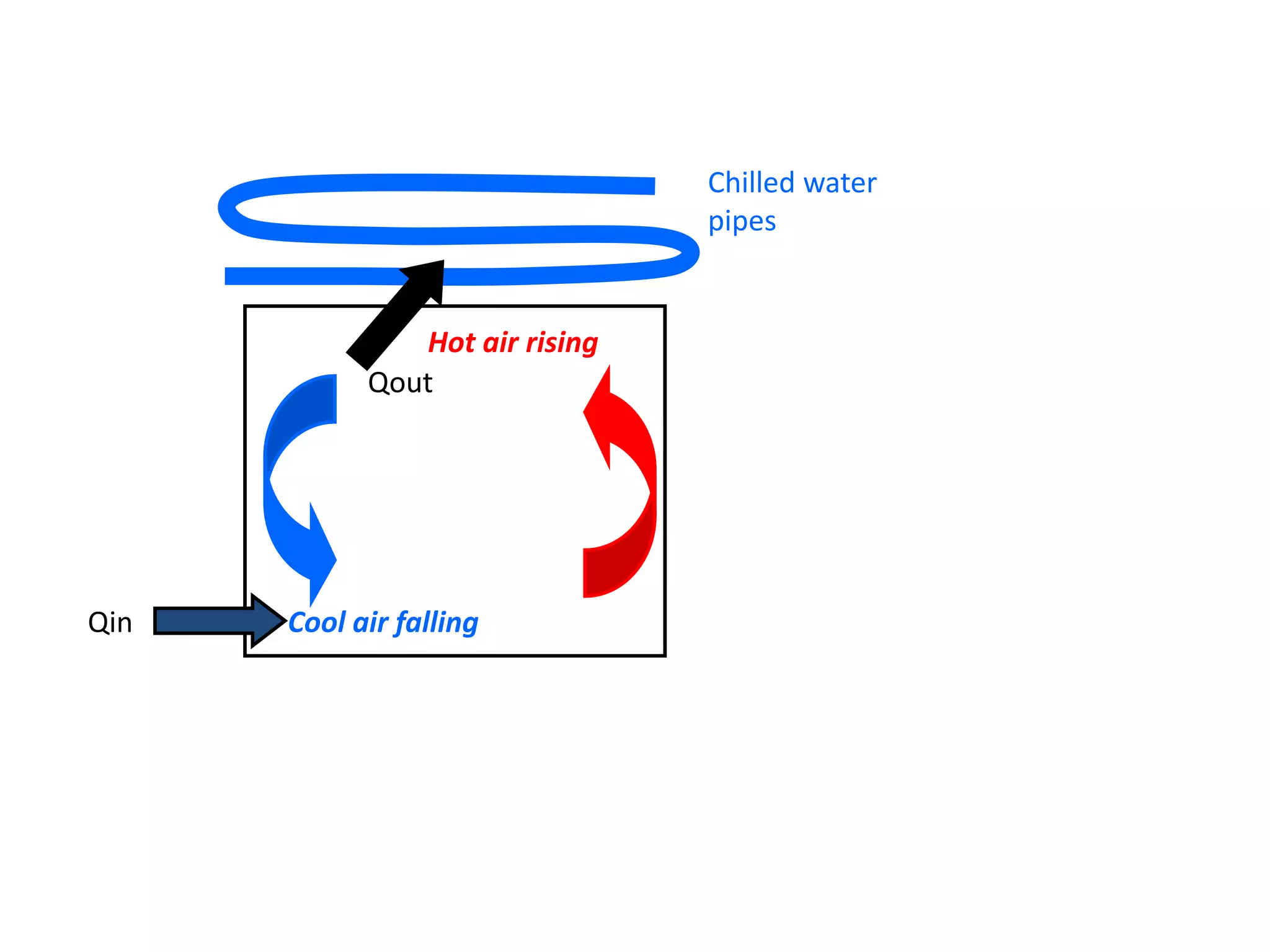
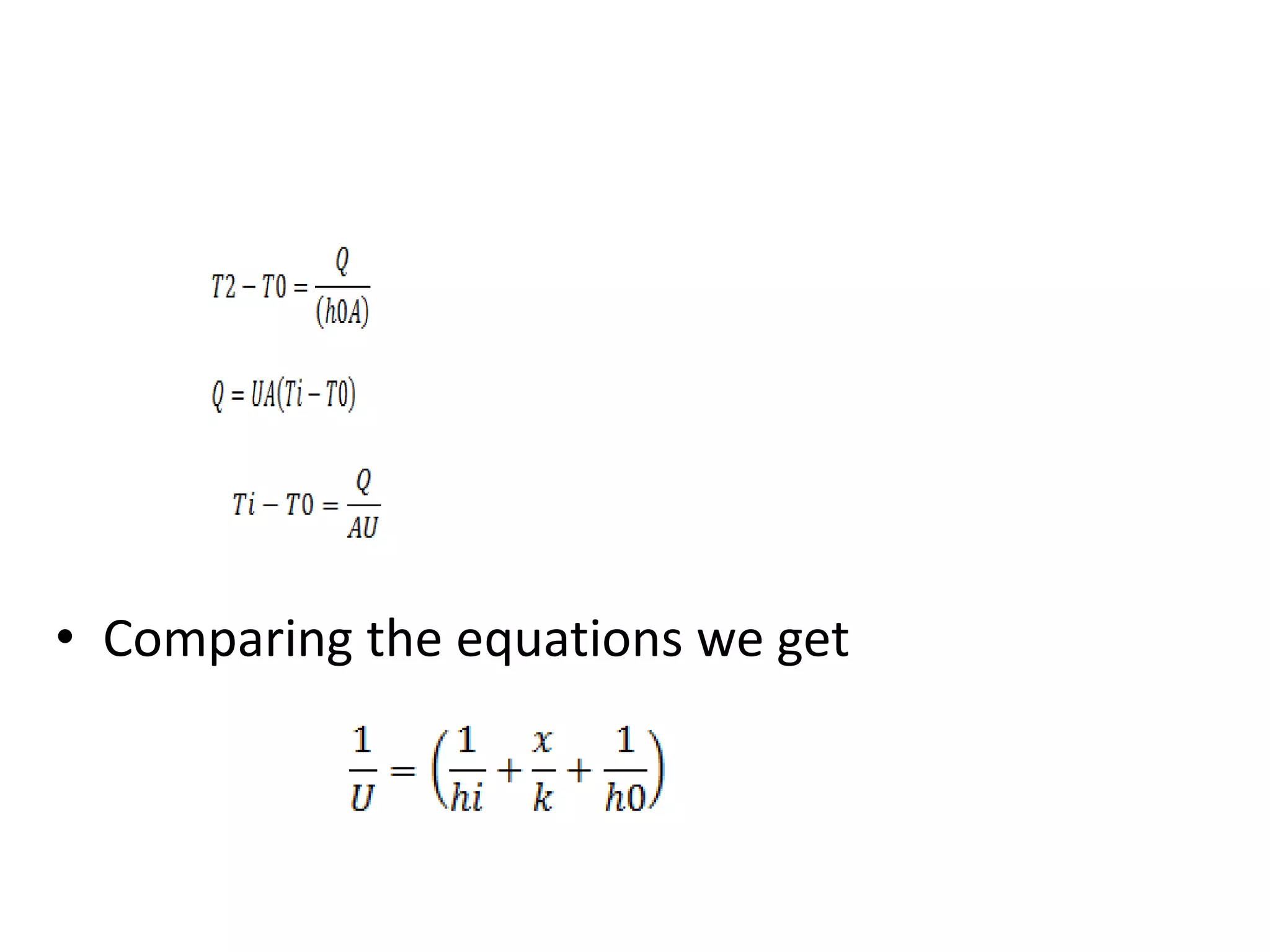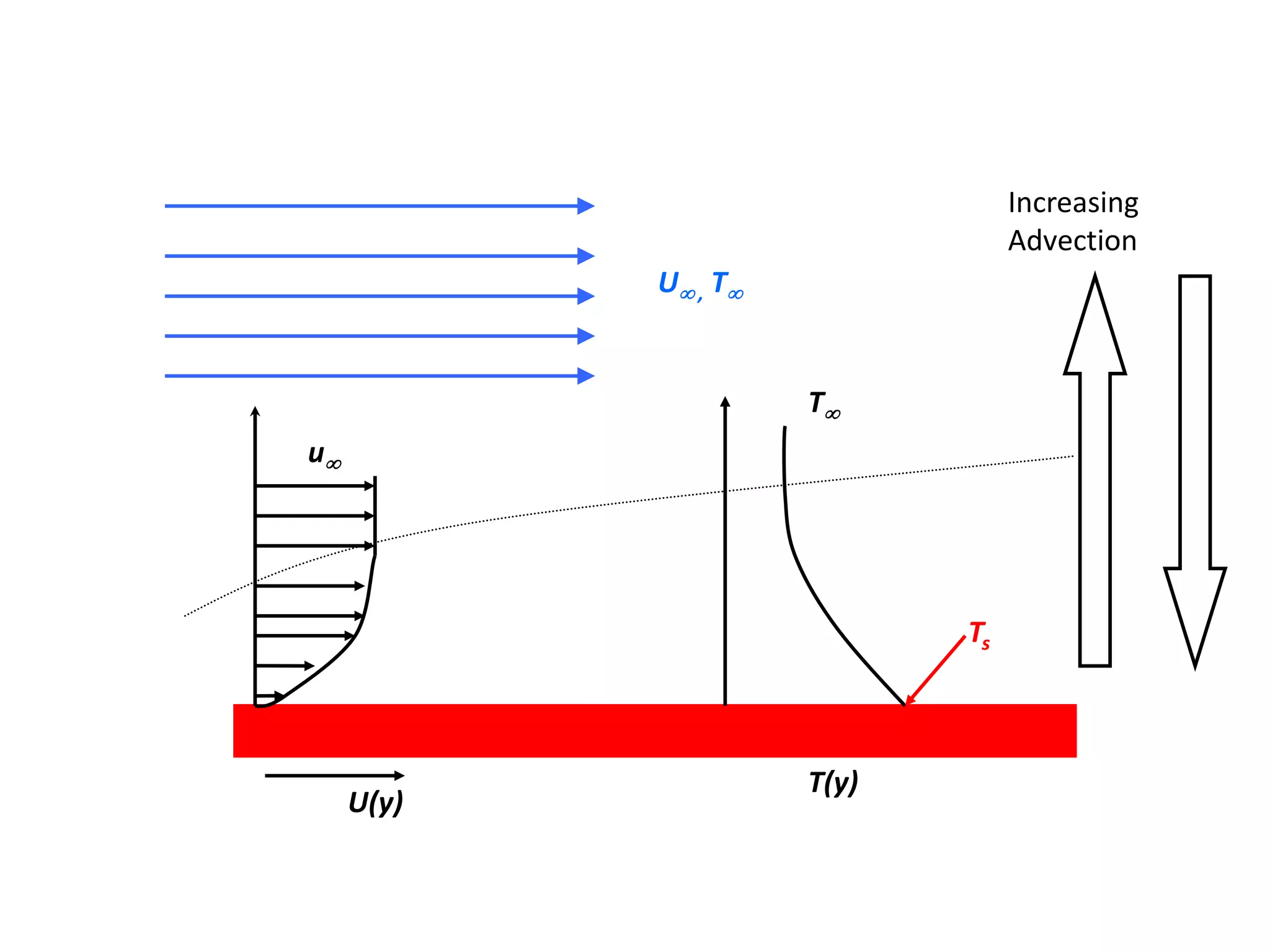
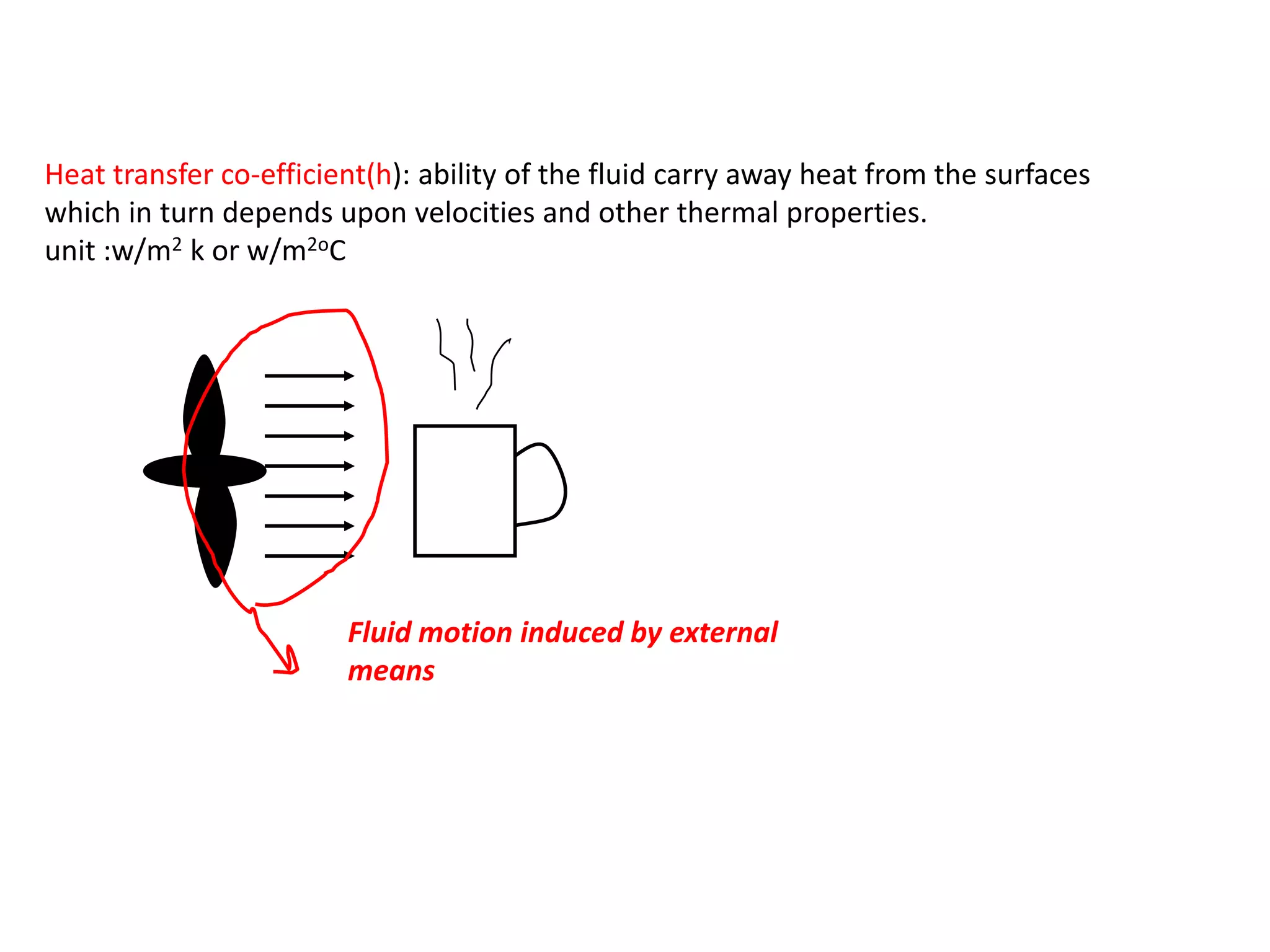
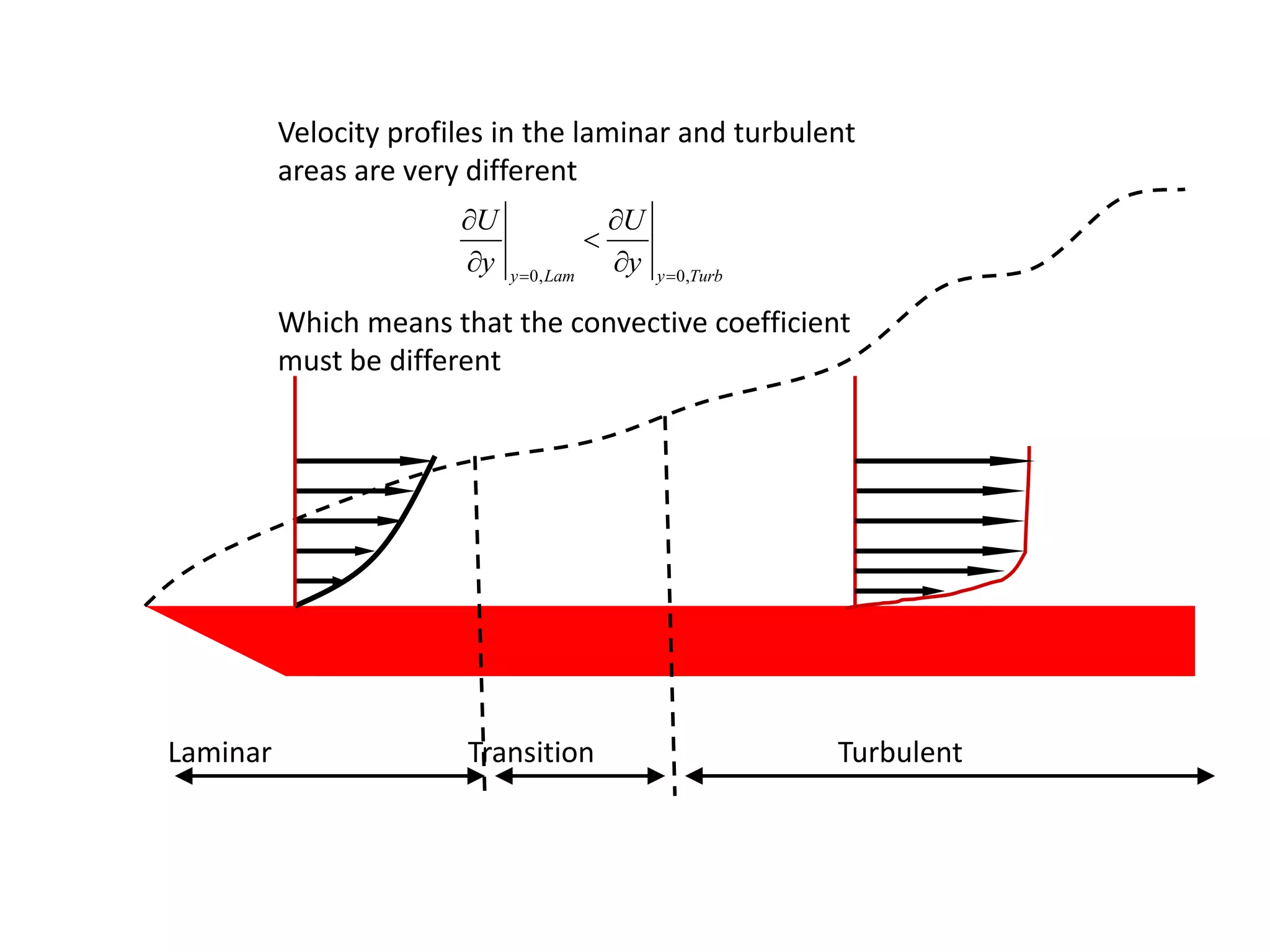
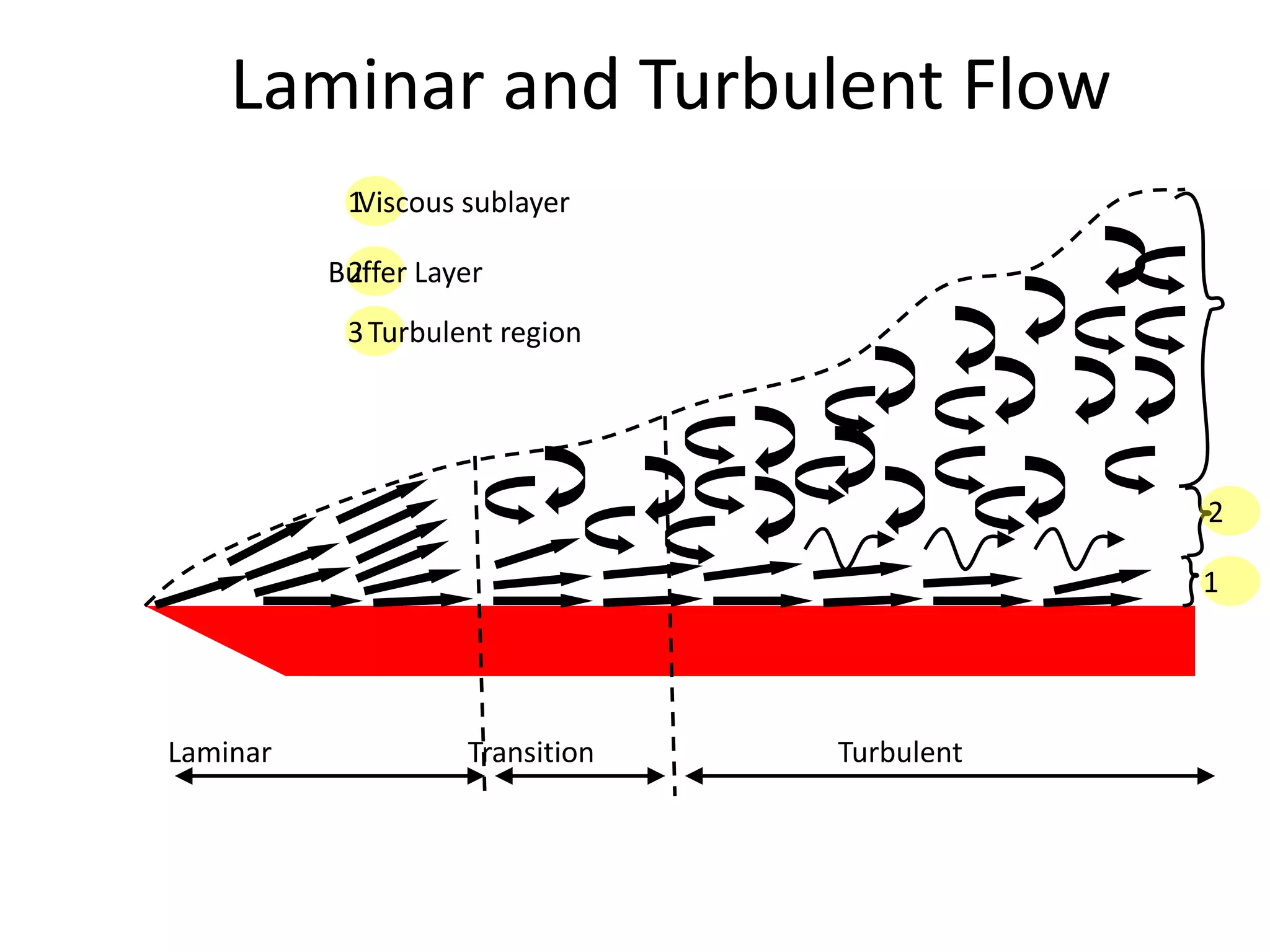
- Heat exchangers transfer heat between fluids through solid surfaces. Heat is transferred by convection between the fluid and solid surface. - The rate of heat transfer depends on the convection heat transfer coefficient (h), which depends on fluid properties and velocities. - Dimensionless numbers like Reynolds, Prandtl, and Nusselt relate fluid flow regime (laminar or turbulent) to heat transfer rate. - Empirical relationships using these numbers predict heat transfer for forced and natural convection in different geometries. - The overall heat transfer coefficient (U) accounts for resistances of conductive and convective boundaries in composite systems.

1. MODULE 3
HEAT EXCHANGERS

2. INTRODUCTION
• When a fluid flows past a stationary solid
surface ,a thin film of fluid is postulated as
existing between the flowing fluid and the
stationary surface
• It is also assumed that all the resistance to
transmission of heat between the flowing fluid
and the body containing the fluid is due to the
film at the stationary surface.

3. Increasing
Advection
U , T
T
u
Ts
T(y)
U(y)

4. Heat transfer co-efficient(h): ability of the fluid carry away heat from the surfaces
which in turn depends upon velocities and other thermal properties.
unit :w/m2 k or w/m2oC
Fluid motion induced by external
means

5. Chilled water
pipes
Hot air rising
Qout
Qin Cool air falling

6. • The amount of heat transferred Q across this film is
given by the convection equation
Where
h: film co-efficient of convective heat transfer,W/m2K
A: area of heat transfer parallel to the direction of fluid
flow, m2.
T1:solid surface temperature, 0C or K
T2: flowing fluid temperature, 0C or K
∆t: temperature difference ,K

7. • Laminar flow of the fluid is encountered at
Re<2100.Turbulent flow is normally at
Re>4000.Sometimes when Re>2100 the fluid
flow regime is considered to be turbulent
• Reynolds number=
• Prandtl number=
• Nusselt number=
• Peclet number=

8. • Grashof number=
• Where in SI system
• D: pipe diameter,m
• V :fluid velocity,m/s
• :fluid density,kg/m3
• μ :fluid dynamic viscosity N.s/m2 or kg/m.s
• ᵧfluid kinematic viscosity, m2/s
:

9. • K:fluid thermal conductivity,w/mK
• h: convective heat transfer coefficient,w/m2.K
• Cp:fluid specific heat transfer,J/Kg.K
• g:acceleration of gravity m/s2
• β:cubical coefficient of expansion of fluid=
• ∆t:temperature difference between surface and fluid ,K

10. Functional Relation Between
Dimensionless Groups in Convective
Heat Transfer
• For fluids flowing without a change of phase(i.e
without boiling or condensation),it has been found
that Nusselt number (Nu) is a function of Prandtl
number(Pr) and Reynolds number(Re) or Grashof
number(Gr).
• Thus for natural convection
• And for forced convection

11. Empirical relationships for Force
Convection
• Laminar Flow in tubes:
• Turbulent Flow in Tubes: For fluids with a
Prandtl number near unity ,Dittus and Boelter
recommend:
• Turbulent Flow among flat plates:
• Problem:

12. Empirical Relationships for natural
convection
• Where a and b are constants. Laminar and
turbulent flow regimes have been observed in
natural convection,10<7<GrPr<109 depending
on the geometry.
• Horizontal Cylinders:
when 104<GrPr<109(laminar flow)and
Nu=0.129(GrPr)0.33

13. when 109<GrPr<1012 (turbulent flow)
Problem:
Vertical surfaces:
Nu=0.59(GrPr)0.25
4
When 10 <GrPr<109(laminar flow)
Nu=0.129(GrPr)0.33
9
When 10 <GrPr<1012 (turbulent flow)
Horizontal flat surfaces:fluid flow is most restricted in the case
of horizontal surfaces.
Nu=0.54(GrPr)0.25

14. 5
When 10 <GrPr<108(laminar flow)
Nu=0.14(GrPr)0.33
8
whenGrPrᵧ10 (turbulent flow)
Problem:

15. Laminar and Turbulent Flow
1Viscous sublayer
Buffer Layer
2
3 Turbulent region
2
1
Laminar Transition Turbulent

16. Velocity profiles in the laminar and turbulent
areas are very different
U U

y y  0, Lam
y y  0,Turb
Which means that the convective coefficient
must be different
Laminar Transition Turbulent

17. OVERALL HEAT TRANSFER CO-EFFICIENT FOR
CONDUCTIVE –CONVECTIVE SYSTEMS
• One of the common process heat transfer
applications consists of heat flow from a hot fluid,
through a solid wall, to a cooler fluid on the other
side. The fluid flowing from one fluid to another fluid
may pass through several resistances, to overcome
all these resistance we use overall heat transfer
• Newton's Law may be conveniently re-written as
Where h=convective heat transfer co-
efficient,W/m2-k

18. • A=area normal to the direction of heat flux,m2
• ∆T=temperature difference between the solid
surface and the fluid,K.
• It is often convenient to express the heat
transfer rate for a combined conductive
convective problem in the form(1),with h
replaced by an overall heat transfer coefficient
U.We now determine U for plane and
cylindrical wall systems.

19. Figure 1
• Plane wall
Or
1/Ahi and 1/Ah0 are known as thermal
resistances due to convective boundaries or
the convective resistances(K/W)
Conductive heat flow Q=kAdt/dx=KA(T1-T2)/x

20. • Comparing the equations we get

21. problems
• Radial Systems
The Fourier law gives