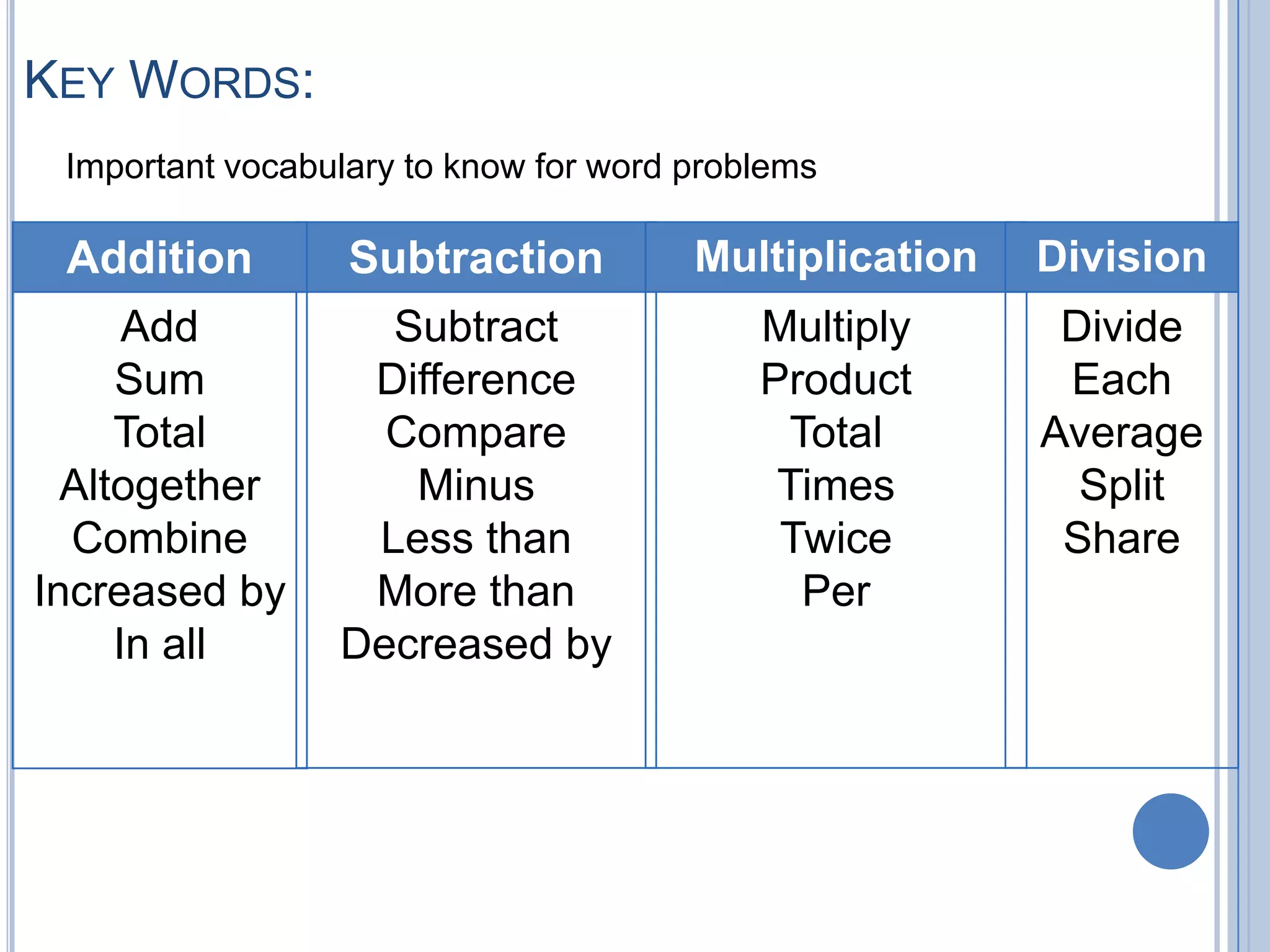
The document provides information for a math class including: - Where to find attendance sheets and the class code. - The teacher's background and why she loves teaching math. - Expectations for success, materials needed, class structure, and guidelines. - An introduction to place value, operations, and solving word problems.

2. ATTENDANCE SHEET
 Attendance sheets can be found on the desk by the
door.
 Every class you need to sign in on your attendance
sheet.
 Our Class code is 12014

3. ORIENTATION

4. ABOUT ME
 Florida Girl
 Crafts and Photography
 Bachelor of Science in Math
 High-school struggle with math
 Especially enjoy helping those who have found
math difficult
 Getting married this year

5. WHY I LOVE MATH
“We all use math every day-
to predict weather, to tell time,
to handle money.
Math is more than formulas and equations.
It's logic. It's rationality. It's using your mind to solve
the biggest mysteries we know.”
-Numb3rs introduction

6. HOW TO SUCCEED
 Time Investment
 Come to every class. Be on time.
 Do class work.
 Faithfully do homework.
 Make learning a priority.
 Emotional Investment
 Be positive & cooperative.
 Have confidence.
 Bounce back.
 Learn something new everyday and review
something everyday

7. MATERIALS YOU NEED FOR CLASS
 3-ring Binder
 Notebook
 Pens
 Pencils
 Paper
 Bring materials to every class!

8. GUIDELINES FOR CLASS
o Come prepared to learn.
o Bring materials and be mentally prepared to
learn
o Be on time.
o 15 mins after class starts you will not be
allowed to attend the class.
o Attend faithfully
o You only have 1 absence for every 4 weeks.
o No cell phone use in class, please silence them
o No calls or texting

9. STRUCTURE FOR CLASS
 Review homework
 Go over some of the homework problems
 Attendance Sheet
 Lesson
 Break
 Lesson

10. EXPECTATIONS..
 What do you expect from a teacher?
 What do you expect from this math class?

11. I EXPECT…
 You to respect me, and I will in turn respect you.
 You to respect others in the class and allow
everyone a chance to learn

12. BRUSH UP ON NEEDED SKILLS
Not knowing a skill can hinder your ability to take the
GED test. It may take longer to figure out a problem.
For example: multiplication facts
One way to brush up on this skill is make some flash
cards and practice daily!

13. VOCABULARY
 Many people miss test questions because they lack
understanding of certain math terms.
 By understanding the meanings of the math terms, the
problems can then be solved correctly .
 So we will be focusing on the math terms as well as the
math process

14. LESSON

15. PLACE VALUE
• Place value is the basis of our entire number system
• Before any numbers can be added, subtracted, multiplied or
divided, the place value of numbers must be understood.
• Each place has a given value, therefore each digit has a
given value.
• A place value system is one in which the position of a digit in
a number determines its value.
Example: 127,854
Hundred Ten
Thousands Hundreds Tens Ones
Thousand Thousand
1 2 7 8 5 4

16. In the number 456, each digit has a specific value.
4 5 6
hundreds tens ones
4 x 100 5 x 10 6x1
The value for each number is as follows:
400 + 50 + 6 =
456

17. PLACE VALUE PRACTICE
 What place value is the number 5 in each of these
numbers:
 5,423
 758
 965
 50,012
 8,652
 588
 501,468

18. GUIDED PRACTICE: PLACE VALUE
Write the value for the underlined number below.
1. 478 ___________
2. 985 ___________
3. 225 ___________
4. 7361 ___________

19. GUIDED PRACTICE: PLACE VALUE
Write the value for the underlined number below.
1. 478 8 ones
___________
2. 985 9 hundreds
___________
3. 225 ___________
2 tens
4. 7361 ___________
7 thousands

20. DECIMAL PLACE VALUE
Example: 0.78216
Ten Hundred
Tenths Hundredths Thousandths
Thousandths Thousandths
7 8 2 1 6

21. DECIMAL PLACE VALUE
 What place value is the 7 in each of these decimals?
 0.127
 0.7
 0.37
 0.4567

22.  Have you notice the pattern for the place values?
 Notice all the decimal place names end in –ths.
 They represent fractions or part of one unit.

23. ESTIMATION
 Estimation is finding a number that is close
enough to the right answer.
 You are not trying to get the exact right answer
 When would be a good time to use estimation in your
life?
 In mathematics we often stress getting an exact
answer.
 But estimation can save you from making mistakes
with your calculator:

24.  For example: you are calculating 107 times 56, and
the calculator shows this:
952.00
Is that right?
 "107 times 56 is a bit more than 100 times 50,
which is 5,000"
 Ooops! you must have typed something wrong, in
fact you pressed 17×56 (you left out the zero), and
without estimating you could have made a really big
mistake!

25. ROUNDING
 Rounding means reducing the digits in a number
while trying to keep its value similar.
 The result is less accurate, but easier to use.
How to Round
 Underline the digit in the place you are rounding to,
this is the last digit you need to keep
 Leave the underlined digit the same if the next
digit to the right is less than 5
 But increase the underlined digit by 1 if the next
digit to the right is 5 or more

26. EXAMPLES OF ROUNDING
 Round 74 to the nearest 10
 Round 86 to the nearest 10
 3.1416 rounded to hundredths
 1.2635 rounded to tenths
 5.7536 rounded to 3 decimal places

27.  Round 0.599 to the hundredths place
 Round 178.9 to the ones place
 Round 84.84 to the tenths place
 Round 0.1254 to the thousandths place

28. IXL.COM
 Rounding
 Level H: B.7

29. WHAT ARE THE 4 BASIC MATH OPERATIONS?
Addition Multiplication
Subtraction Division
It doesn’t matter what kind of math problems are being
solved. These are the only math operations used.

30. DEFINITIONS: BASIC OPERATIONS
 Addition (+) Adding two or more numbers together.
 Subtraction (-) Finding the difference between numbers.
 Multiplication (x) is repeated addition.
 5 x 3 is the same as 5 + 5 + 5 or 3 sets of 5 = 15
 3 x 5 is the same as 3 + 3 + 3 + 3 + 3 or 5 sets of 3 = 15
 Division (÷) is the splitting into equal groups or parts; the result of
sharing.
There are 12 chocolates, and 3 friends want to share them, how
do are the chocolates divided?
4 each

31. ADDITION AND SUBTRACTION ARE
OPPOSITE OPERATIONS
75+25=100 AND 100-25=75

32. MULTIPLICATION
 Always think of multiplication as just adding groups
of numbers.
 If you have 4 x 3, it simply means 4 groups of 3.
 Within these four groups, there are three triangles.
3 3 3 3
How many triangles? 3 + 3 + 3 + 3=12
4 groups of 3 = 12 4 x 3= 12

33.  The numbers multiplied together in a multiplication
problem are known as factors.
 In 3 x 6 = 18; 3 and 6 are the factors of this problem
 3 and 6 are factors of 18
 The answer to a multiplication problem is know as
the product.
 In 3 x 6 = 18, the answer 18 is the product.

34. MULTIPLICATION SYMBOLS
 The multiplication problems can be written in many
forms –
 The format that is most recognizable is using the “x”
between two numbers:
 Example: 2 x 3
 Using a dot between numbers also means multiply.
 Example 5 • 4
 Parenthesis around a number means multiply.
 Example: (9)(6)
 Example: 5(3)
 Algebraic expression
 Example: 5n = (5 x n)

37. DIVISION SYMBOLS

38. “SIXTY-EIGHT DIVIDED BY TWO”


39. 

40. MULTIPLICATION AND DIVISION ARE
OPPOSITE OPERATIONS
 For each division fact, there is another division fact.
 For example:
72 9=8 and 72 8=9
 For each of those division facts, there is a related
multiplication fact.
 For example:
8 x 9 = 72 and 9 x 8 = 72

41. HOW TO SOLVE WORD PROBLEMS
 Word problems often scare people. There is no secret to
solving word problems. Experience and practice are the
best help. But you can use these 5 steps to organize your
thinking about word problems.
1. Understand the question--What is the problem asking?
2. Decide what information is needed to solve the
problem.
3. What operations will be used?
4. Solve the problem and check your work
5. Does the answer make sense and did you answer the
question being asked?

42. SOLVING WORD PROBLEMS
 There are 3 main tools for solving word problems:
1. Knowing the definitions or main idea behind the different
operations.
2. Knowing the Key Words for choosing the correct operation.
3. Asking the right questions when solving the word problem.

43. KEY WORDS:
Important vocabulary to know for word problems
Addition Subtraction Multiplication Division
Add Subtract Multiply Divide
Sum Difference Product Each
Total Compare Total Average
Altogether Minus Times Split
Combine Less than Twice Share
Increased by More than Per
In all Decreased by

44. KEY WORDS VS. MAIN IDEA
 Shawna was sick and running a fever. In the
morning her temperature was only 99.6 F. By 3:00
in the afternoon it had climbed to 103.2 F. How
much did her temperature increase?
 Key Words?
 Increase– Addition
 Main Idea?
 Difference in temperature– Subtraction
 Which to believe?
 The main idea
 Answer?
 103.2-99.6=3.6 degrees

45.  Maxine can type 65 words per minute. How many
minutes will she need to type a document that
contains 2600 words?
 A. 25
 B. 30
 C. 35
 D. 40
 E. 45
 Answer?
 D. 40

46. MULTI-STEP WORD PROBLEM
 Sam and Eric earned $500 moving a family across town.
They use $75 of that money to pay for renting the truck and
buying gas. If they split the rest of the money evenly, how
much money will each man get?
 Key Word/idea?
 Profit- earnings after expenses
 Steps:
 How much money is left over after they pay for the truck
and gas?
 500-75=425
 How much does each man get?
 425/2= $212.5

47. 1. Jan went to the market to buy tailgating food. She
bought 2 bags of chips for $2.69 each, hotdogs for
$2.49 and buns for $1.29. How much did she
spend altogether? $9.16
2. Anna is having a party. She is buying pizza for
everyone. She invited 14 people, so she is
ordering 4 pizzas at a cost of
$10.98, $14.63, $8.98, and $12.76. What is the
total cost of the pizzas? She gave the delivery
guy $50.00. How much change will she get back?
Total: $47.35 and $2.65 in change

48. 1. Steve is going in the store to get his friends a
bottle of water. He needs to purchase 5 bottles at
a cost of 1.49 each. What is his total cost, before
tax?
$7.45
2. Frank has a new car. He needs to know how
much to budget for gas each month. His car will
hold 14 gallons, total. If gas is $3.12 per gallon,
how much will the cost of a complete fill-up be?
$43.68

49. 

50. 

51. IN CLASS WORKSHEET
 Page 51

52. IXL ASSIGNMENTS
 Level E.I.4 (Addition, Subtraction, Multiplication, and
Division Word Problems)
 Level J. E.5 (Multiply and Divide Word Problems)
 Level H. M.2 (Word problems with multiple steps or extra
or missing information)
 Level E: I.6 (Multi-Step Word Problems)