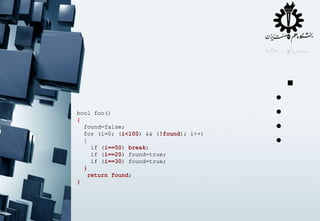
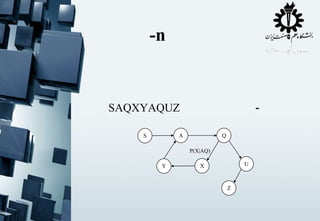
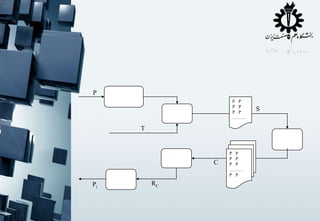
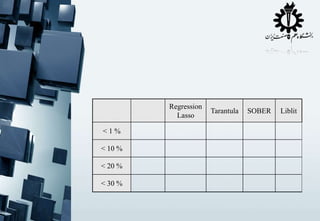
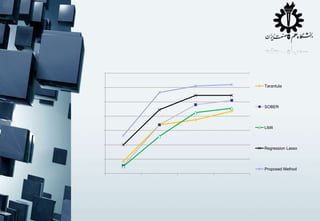
The document contains fragmented code snippets and mathematical expressions related to programming logic, algorithm implementation, and statistical measures. It discusses the behavior of functions, likelihood computations, and performance metrics for text-based modeling techniques such as unigrams, bigrams, and trigrams. Additionally, there are references to error testing methodologies and regression analysis in the context of algorithm evaluation.

2. -n

4. 
int *a = new ….
.
.
.
If (a>22)
(a>2)
(a[0] >22)
fail();
else
.
.
.
•
•
•
•




6. ◄
–n
-n ◄
◄

7. bool foo()
{
found=false;
for (i=0; (i<100) && (!found); i++)
(
)
(
);
{
if (i==50) break;
(
)
;
if (i==20) found=true;
(
)
if (i==30) found=true;
(
)
}
return found;
;
}
•
•
•
•


9. 


void foo()
{
found=false;
for (i=0; (i<100) && (!found) ;i++)
{
if (i==50) break;
if (i==20) found=true;
if (i==30) found=true;
}
printf("foon");
}


11. -n
-n
-n
n-1
≈

12. -n
P(w|h)
h
w
p( w | w1n )
n 1
1
p( wn | w )
C ( w1n 1wn )
C (w1n 1 )

13. -n
-N
p ( wn | w1n 1 )
bigram, N
n
p ( wn | wn
2
1
N 1
)
n 1
1
p( wn | w
)
p( wn | wn 1 )

14. -n
n
p(wn | wn
1
N 1
)
n
C (wn 1 1wn )
N
n
C (wn 1 1 )
N
p( w1n )n ) p( w1 |# ) pp( w2| |w11 ) p(( w3| |w122)) .... p(( wn | |w1nn 11))
p( w1
p( w1 ) ( w2 w) p w3 w .... p wn w
n n
p( wk |k wk 1k)1 )
p( w | w
k 1 1
k

15. -n
-
SAQXYAQUZ
A
S
Q
P(X|AQ)
Y
U
X
Z

16. -n

17. H ( p)
H (X )
p ( x) log p ( x)
x X
p
X

18. q p
H ( p, q )
E p ( log q )
DKL ( p || q )
H ( p)
H ( p)
p ( x ) log q ( x )
x
H ( p, q )
p ( x ) log q ( x )
x
DKL ( p || q )

19. H ( p, q)
H ( p) , if p
H ( p, q)
H ( p, q)
H ( p, q)
H (q, p)
q

20. -n
-n
p(win ) log p(wn | win 1 )
H(X )
w*
-n
p X (win ) log pY (wn | win 1 )
H ( X ,Y )
w*

21. P
P P
P P
P P
………
T
C
Pi
RC
P P
P P
P P
………
P P
S

22. Y X
X=p1 p2 p3
Y=p1 p2 p4
p X ( win ) log pY ( wn | win 1 )
H ( X ,Y )
w*
p X ( win ) log pY ( wn | win 1 )
p X1,(pP1P122, p3)3, p1 ppp 3}( P1) p X ( P2 | P1) p X ( P3 | P1P 2)
{ p 2 , p 3, p p P 2 p
2X
p X ( P1) log pY ( P1 |# )
p X ( P 2) log pY ( P 2 |# )
p X ( P3) log pY ( P3 |# )
p X ( P1P 2) log CY PPP 2) 1)1 p X ( P 2 P3) log pY(( P3 | P 2)
p( ( 1 2 | P
C P 2) 1
pY ( P 2 | P1)
1 , p X ( P 2)
C pY ( P 1
C ( wii 1 ) 3
p X ( P1P 2 P3) log ( P1) 3 | P1P 2)

23. log0
Y = P1 P2 P4
log 0 0
p X ( P 2 P3) pY ( P3 | P 2)
1
log 0 log(
)
1 C (ngram)
C ( P 2 P3)
pY ( P3 | P 2)
C ( P 2)
0
1
0
1
3

24. 1.60
2.28
2.46
1.79
3.65
2.84
P1 P2 P3 P4 P5
P1
P1 P2
P1 P2 P1 P2
P1 P2 P3 P4
P1
P2
P3
P3
P6
P2
P3
P4
P1
P7
P3
P4
P5
P2
P8
P4
P6
P6
P4
P9
1
2
3
4
5
6

25. P1 P2 P3 P4 =
Unigram {P1,P2,P3,P4},
Bigram {P1P2,P2P3,P3P4},
Trigram {P1P2P3,P2P3P4}
D f ( s)
CrossEntro py( s, ti ) , ti is a fail test
i C
D p (s)
CrossEntro py( s, ti ) , ti is a pass test
i C
Similarity
1
Difference

26. x
y
S
S
S

27. y
Θ
tan( )
0
2
y
x
y
x
tan
, tan
Sf
Dp
Sp
Df
1
y
x

28. priority(ngram)
score(ngram)
ingram
N
k
c 1
( priority(ngram))c

29. Regression
Lasso
<1%
< 10 %
< 20 %
< 30 %
Tarantula
SOBER
Liblit

30. Tarantula
SOBER
Liblit
Regression Lasso
Proposed Method