1. Ìýäýýëëèéí ñèñòåì, àëãîðèòìèéí ¿íäýñ Ëåêö ¹16

2. Àãóóëãà 1. Ðåóðñèâ ôóíêö

3. ¯íýíäýý n óðòòàé àþóëã¿é ãèíæ¿¿äèéã • õàð òóãàëãàí ýðõèýýð òºãññºí ãèíæ • ïëóòîíè ýðõèýýð òºãññºí ãèíæ ãýñýí õî¸ð á¿ëýãò õóâààæ àþóëã¿é ãèíæéè òîîã c(n), n óðòòàé àþóëã¿é ãèíæèéí òîîã I(n) ïëóòîíè ýðõýýð òºãññºí n óðòòàé àþóëã¿é ãèíæèéí òîîã p(n) ãýæ òýìäýãëýâýë c(n)=I(n)+p(n) áàéõ íü ìýäýýæ.

4. ªºðººð õýëáýë; I(n)=c(n-1) (1) p(n)=I(n-1) p(n)=I(n-1)=c(n-2) Èéì ó÷ðààñ áèä c(n)=I(n)+p(n)=c(n-1)+c(n-2) áóþó c(n)=c(n-1)+c(n-2) òîìü¸ã ãàðãàëàà. Äýýðõ áîäëîãûã äàðààõààð áè÷èæ áîëíî.

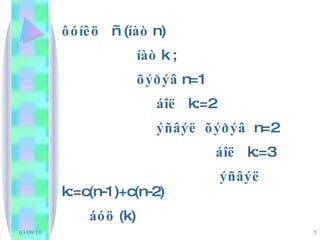
5. ôóíêö ñ ( íàò n) íàò k ; õýðýâ n=1 áîë k:=2 ýñâýë õýðýâ n=2 áîë k:=3 ýñâýë k:=c(n-1)+c(n-2) áóö (k)

6. Ýíý øèéäèéí òóñëàìæòàéãààð ò¿¿íèé çºâ øèéäèéã ÿàæ îëîõ âý? Ýíý ôóíêö áèåëýõ ïðîöåññ ºìíºõ æèøýýíèéíõýýñ èë¿¿ ýýäðýýýòýé òóë c(5) c(5) n=5 c(4) n=4 c(3) n=3 c(2) n=2 k=2

7. áóö (3) c(1) n=1 k=2 áóö (2) k=3+2 áóö(5) c=(2) n=2 k=3 áóö(3) k=5+3 áóö(8)

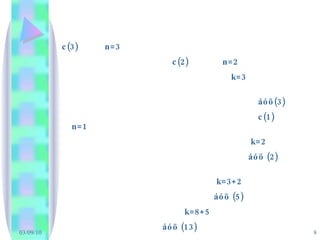
8. c(3) n=3 c(2) n=2 k=3 áóö(3) c(1) n=1 k=2 áóö (2) k=3+2 áóö (5) k=8+5 áóö (13)

9. Õ¿ñíýãòýýñ õàðàõàä ôóíêö ººðèé㺺 8 óäàà äóóäñàí áàéíà. Òýãýõäýý ñ(3),ñ(1) òóñ á¿ð õî¸ð óäàà, (2) ãóðâàí óäàà áîäîãäîæ áàéãàà íü ðåêóðñèâ àðãûí íýã ñóë òàë þì.ªºðºº õýëáýë, ðåêóðñèâ àëãîðèòì áèåëýõ ¿åä íýã óòãûã äàõèí äàõèí áîäîõ òîõèîëäîë ãàð÷ áîëíî.

10. Æèøýý íü: t 1 ,t 2 ,…….t n (á¿õ i -ãèéí õóâüä t i –íàòóðàë òîî áàéõ ) óòãàòàé n øèðõýã äýâñãýðò òºãðºã õýðýãëýäýã îðîíä ºãñºí Ì òºãðºãèéã ýíý äýâñãýðò¿¿äýýð çàäàëæ áîëîõ á¿õ áîëîìæèéí òîîã îëîõ ôóíêö çîõèî.

11. Ýõëýýä çàäëàõ òºãðºã, çàäëàõàä àøèãëàõ äýâñãýðòèéí òîî ôóíêö áèåòýõ ¿åä ººð÷ëºãäºæ áîëîõ óòãóóä ó÷ðààñ ýíý õî¸ð õýìæèãäýõ¿¿íèéã õèéñâýð àðãóìåíò áîëãîí òîäîðõîéëîõ íü ç¿éòýé. Èéì ó÷ðààñ m òºãðºãèéã t 1 ,t 2 ,…….t n õ¿ñíýãòýýð ºãºäñºí n òîîíû äýâýñãýðòýýð çàäëàõ òîîã îëîõ ch (íàò m,n) ôóíêöèéã çîõèîæ áè÷üå.

12. à.n-ä¿ãýýð òºãðºãèéã îðóóëàõã¿é çàäëàõ á¿õ áîëîìæèéã òîî áóþó ch (m,n-1) óòãûã îëîõ á.n ä¿ãýýð äýâñãýðò íýãèéã àâ÷ ¿ëäñýí òºãðºãèéã çàäëàõ á¿õ áîëîìæèéí òîî áóþó ch (m-t n ,n) óòãûã îëîõ .

13. ôóíêö ch(íàò m;n) íàò ó; õýðýâ n=1 áîë õýðýâ m ‡ 0 and m\t 1 =0 áîë y:=1 ýñâýë y:=0 ýñâýë ó:ch(m,n-1) õýðýâ m=t n

14. áîë ó:1+ y ýñâýë õýðýâ m > t n áîë y:=y+ ch(m-t n , n) áóö(y); m òºãðºãèéí t1 äýâñãýðýýð çàäàëæ ÷àäàõ ýñýõèéã øàëãàõäàà äàâõàð m ‡ 0 íºõöëèéã ýíä äàâõàð øàëãàæ áàéãàà þì.

15. Ðåêóðñèâ àðãà íü óãààñàà ðåêóðñèâýýð òîäîðõîéëîãäñîí áîäëîãûã áîäîõîä áîëîí ººð àðãààð áîäîõîä íèéëýýä õ¿íä áàéõ òèéì áîäëîãûí àëãîðèòìûã çîõèîõîä õýðýãëýãääýã ìàø õ¿÷òýé õýðýãñýë þì.

16. Ðåêóðñèâ õàíäàëòûã êîìïüþòåðò õýðýãæ¿¿ëñýí áàéäëààñ õàìààð÷ ðåêóðñèâ àëãîðèòìòàé ïðîãðàì ìàø óäààí áèåëýõ òîõèîëäîë ãàð÷ áîëíî.Èéì àëãîðèòì ïðîãðàìûã çîõèîæ áýëýí áîëãîõîä çàðöóóëàõ õóãàöàà áîëîí ïðîãðàìûã áèåë¿¿ëýõ

17. ¿åèéí (áèåëýõ õóãàöàà áà øààðäàãäàõ ñàíàõ îéí õýìæýý çýðýã ) ºðòºã õî¸ðûã ¿íäýñëýí ðåêóðñèâ àðãûã õýðýãëýõ ýñýõýý øèéäâýë çîõèíî.