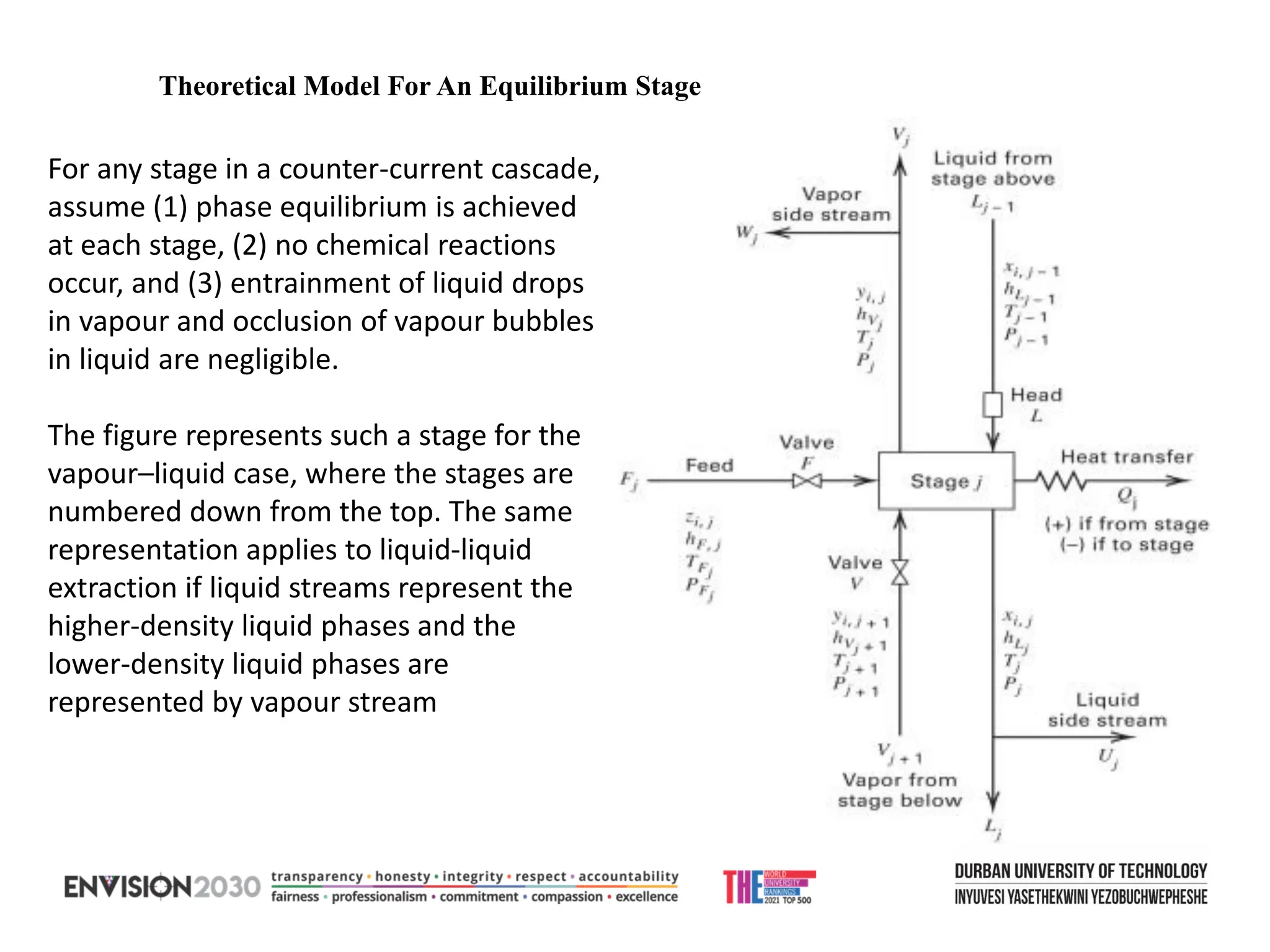
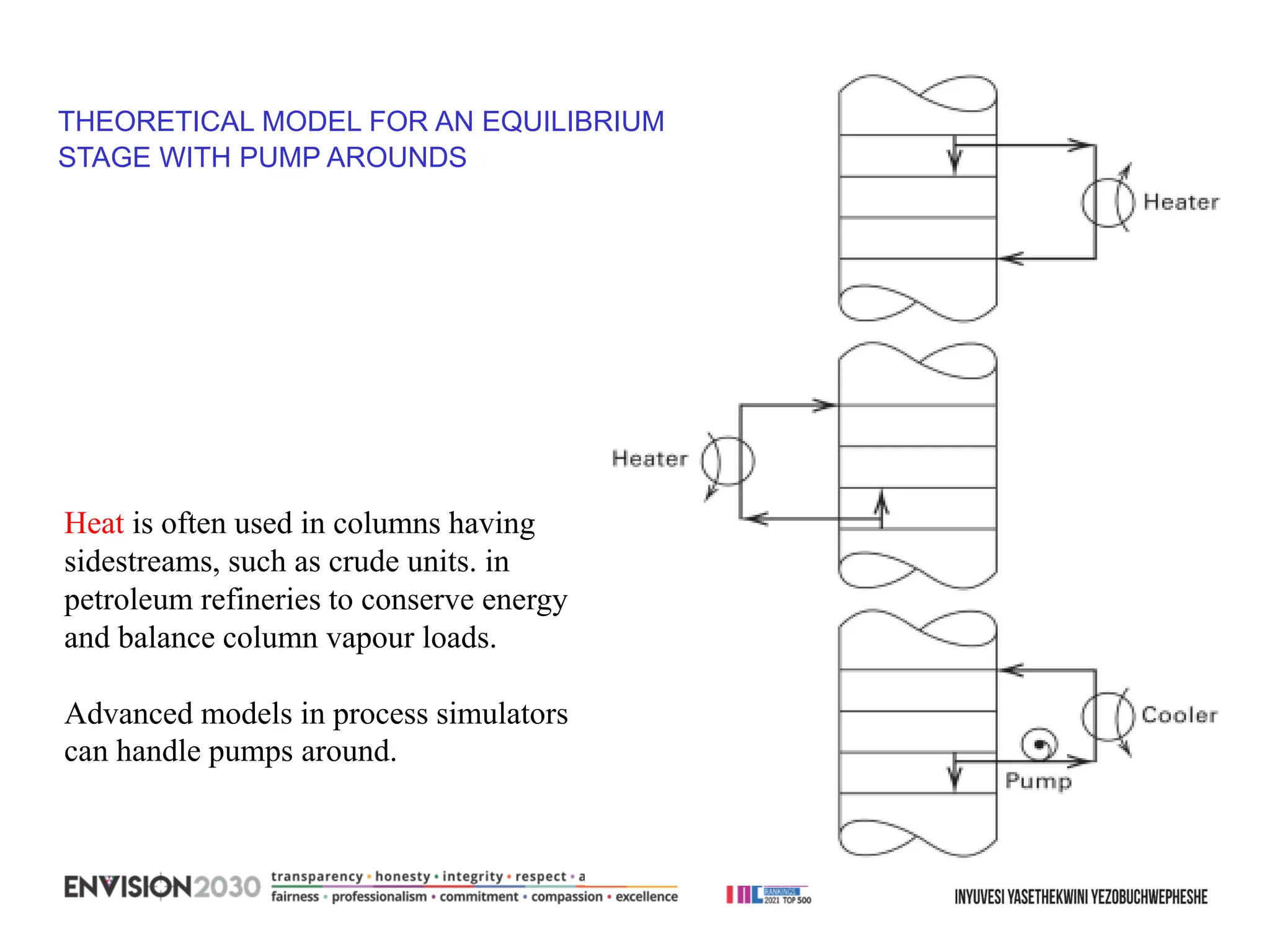
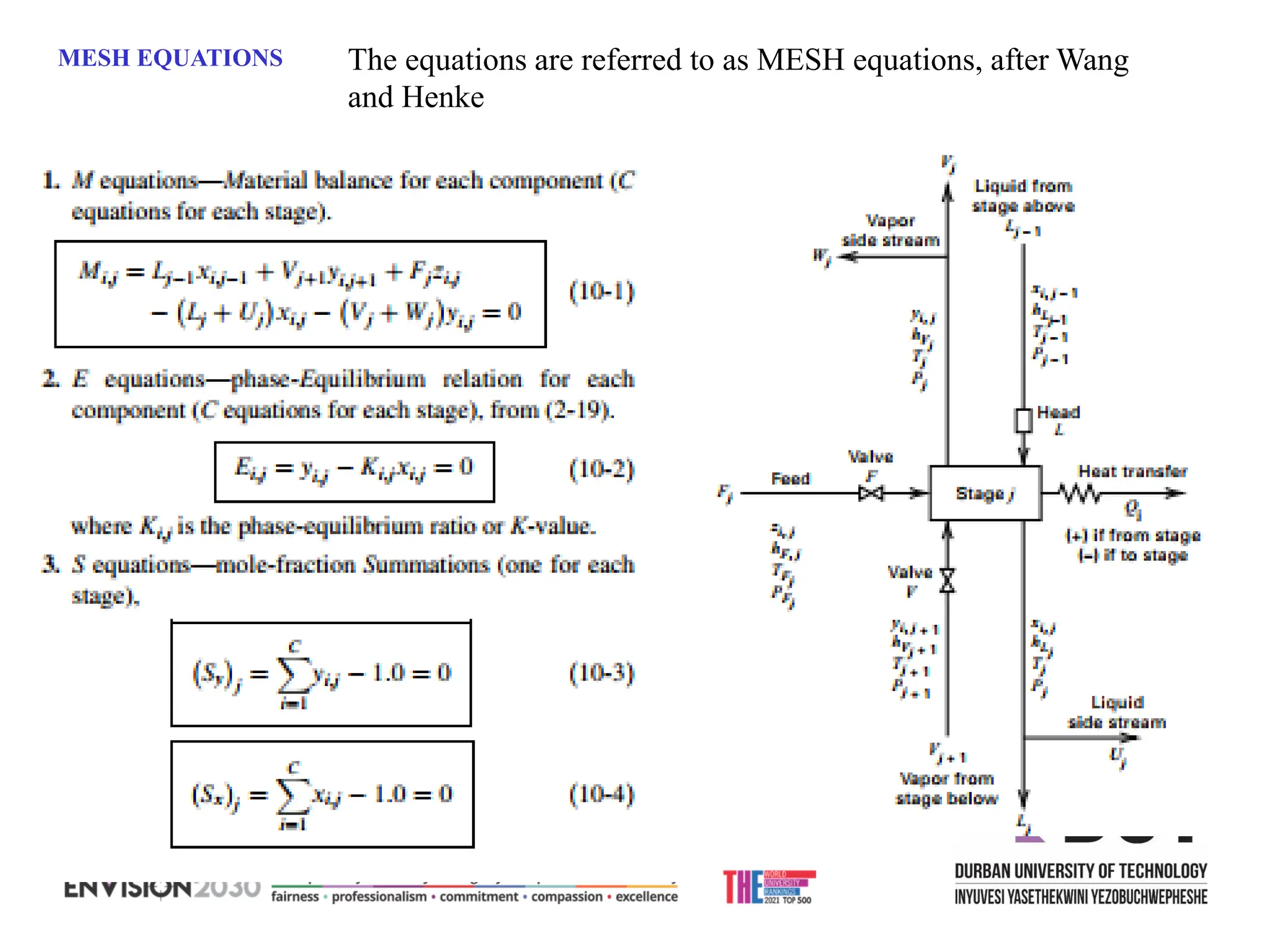
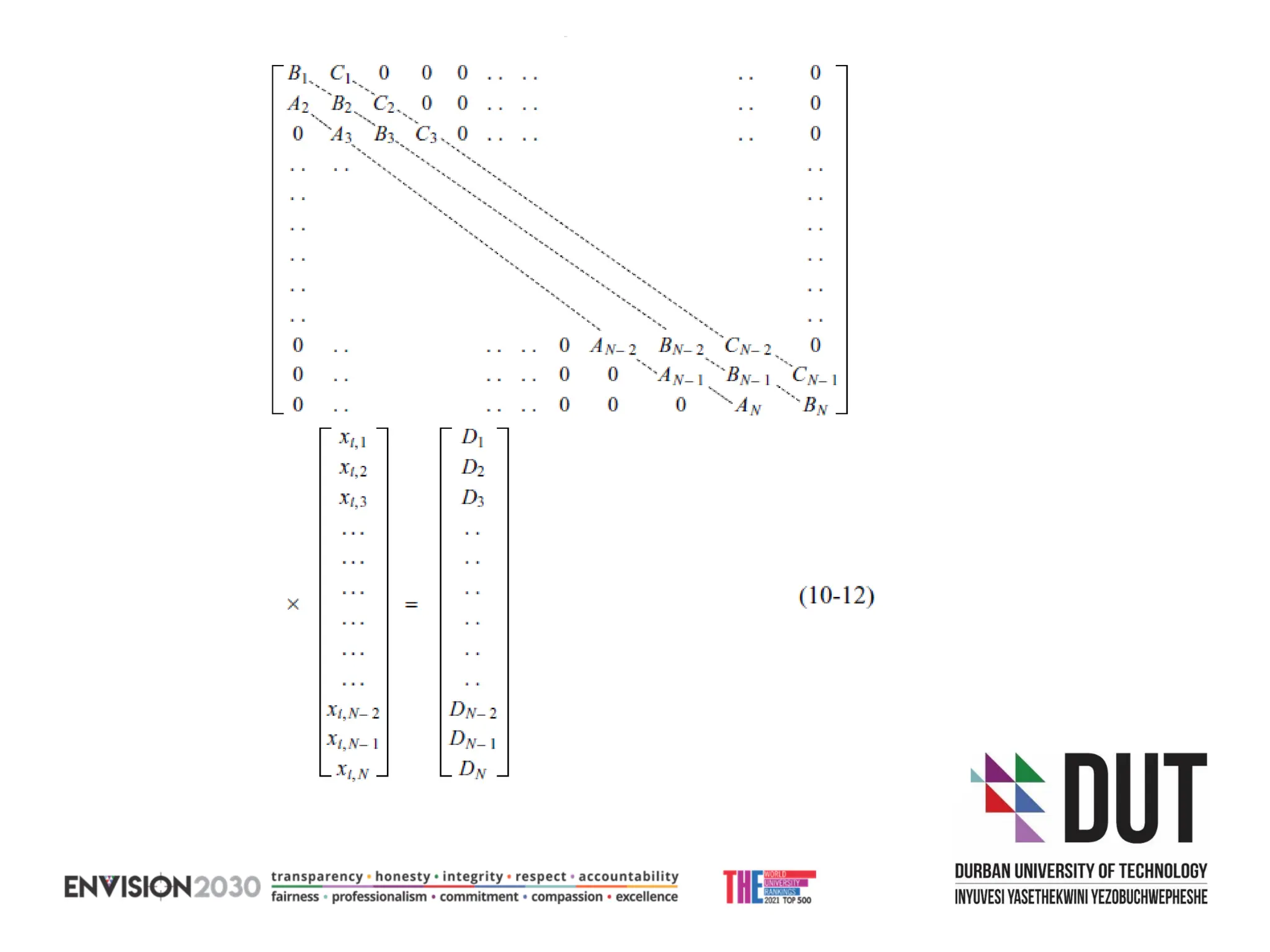
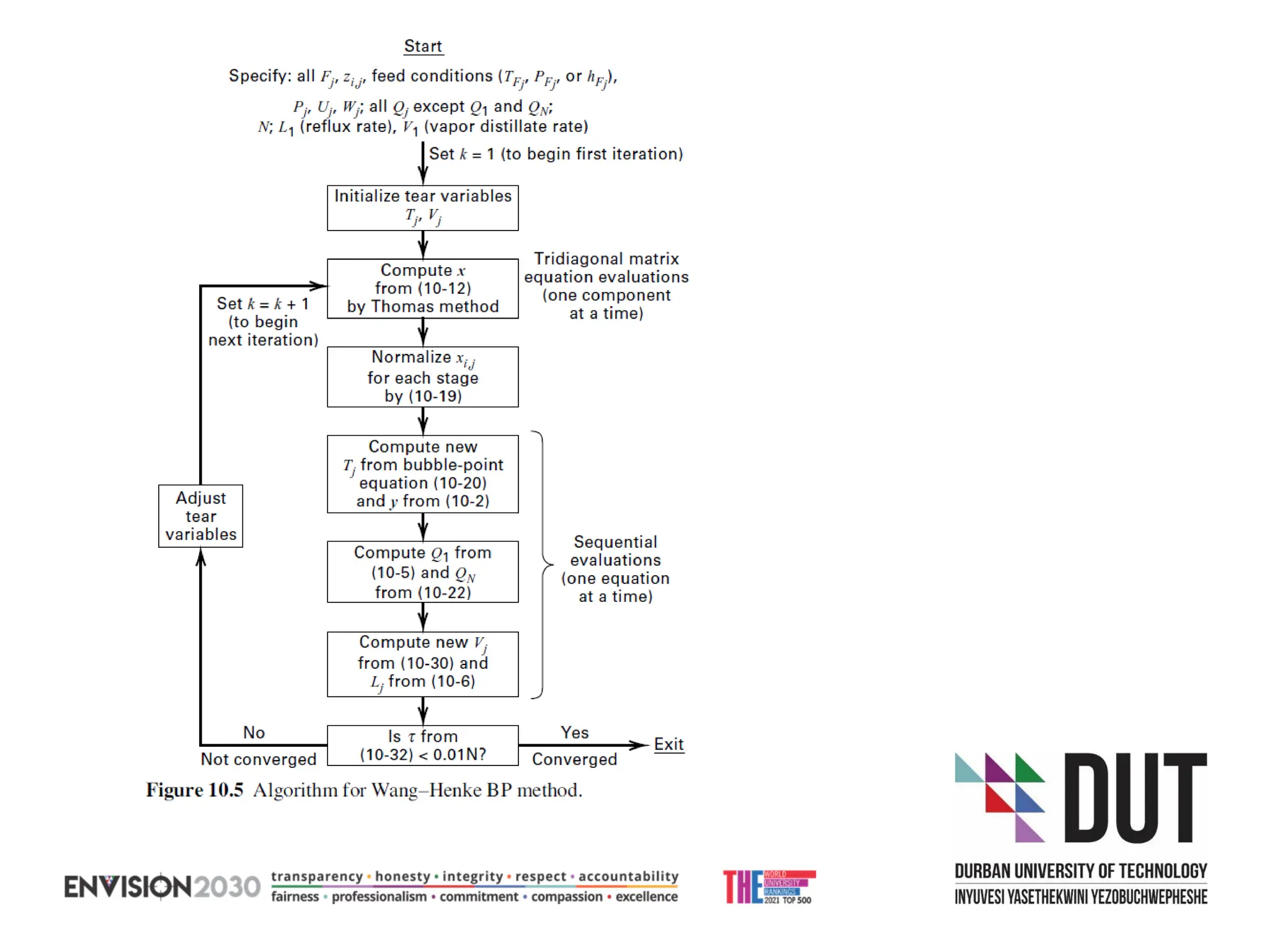
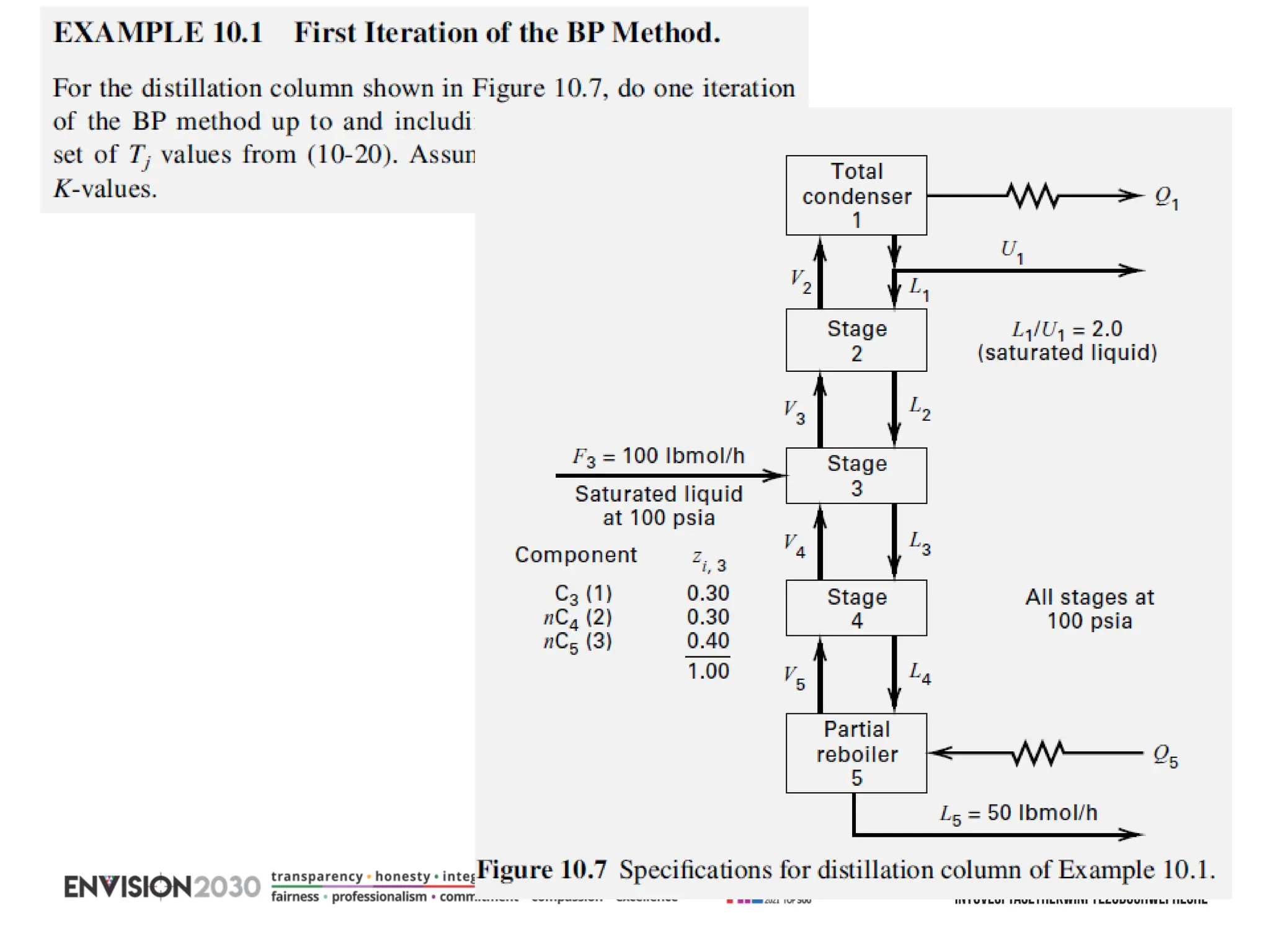
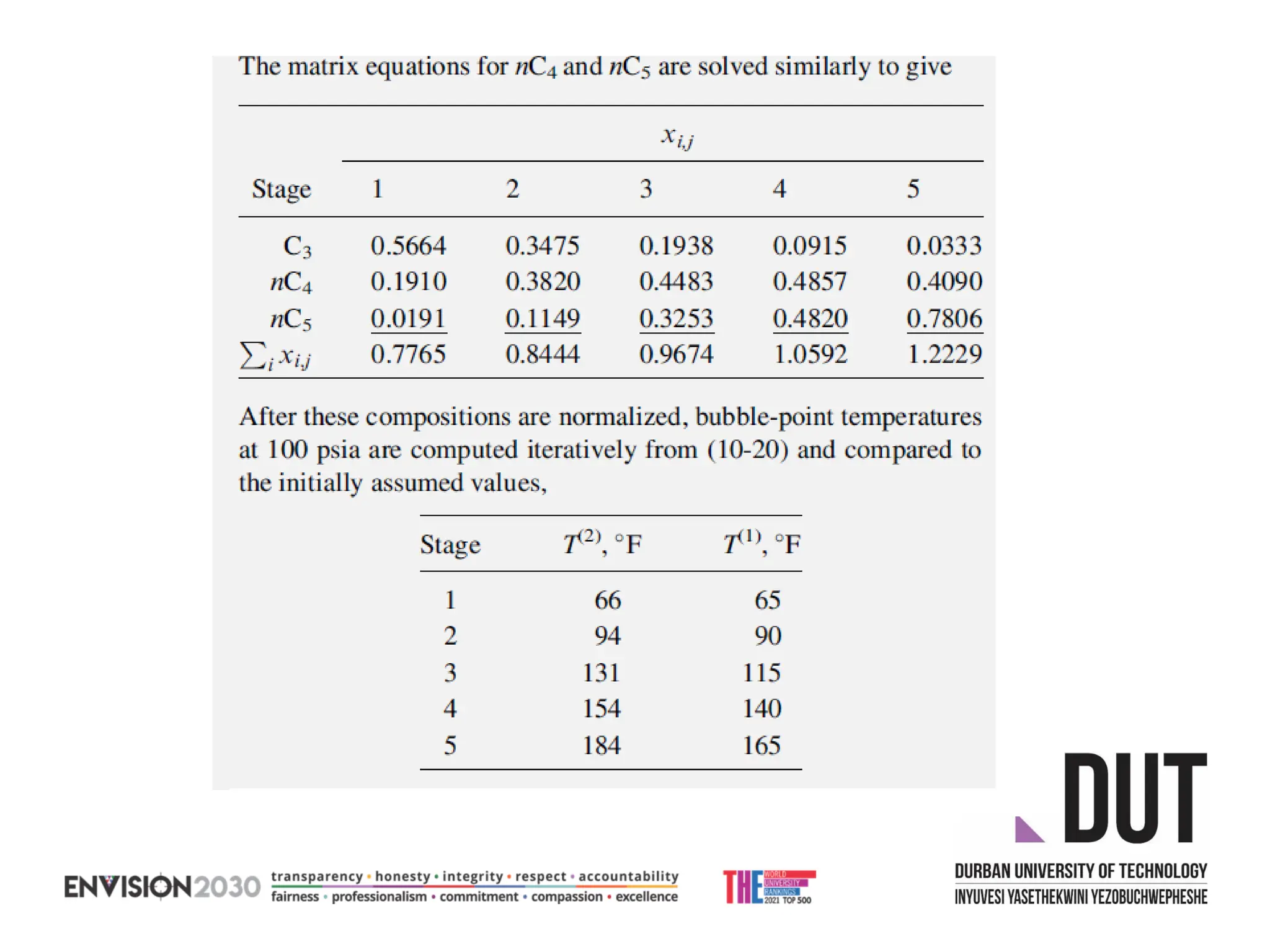
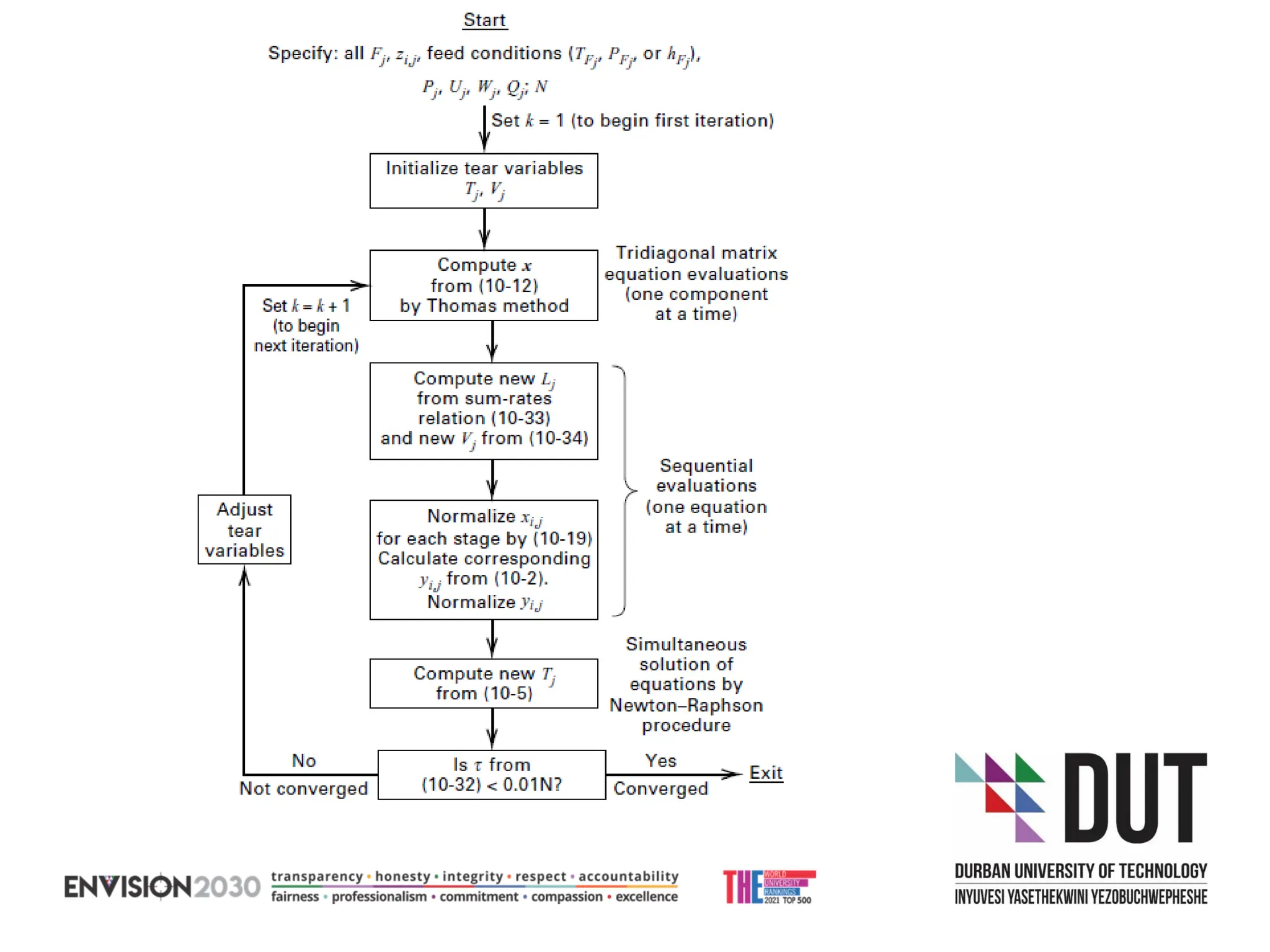
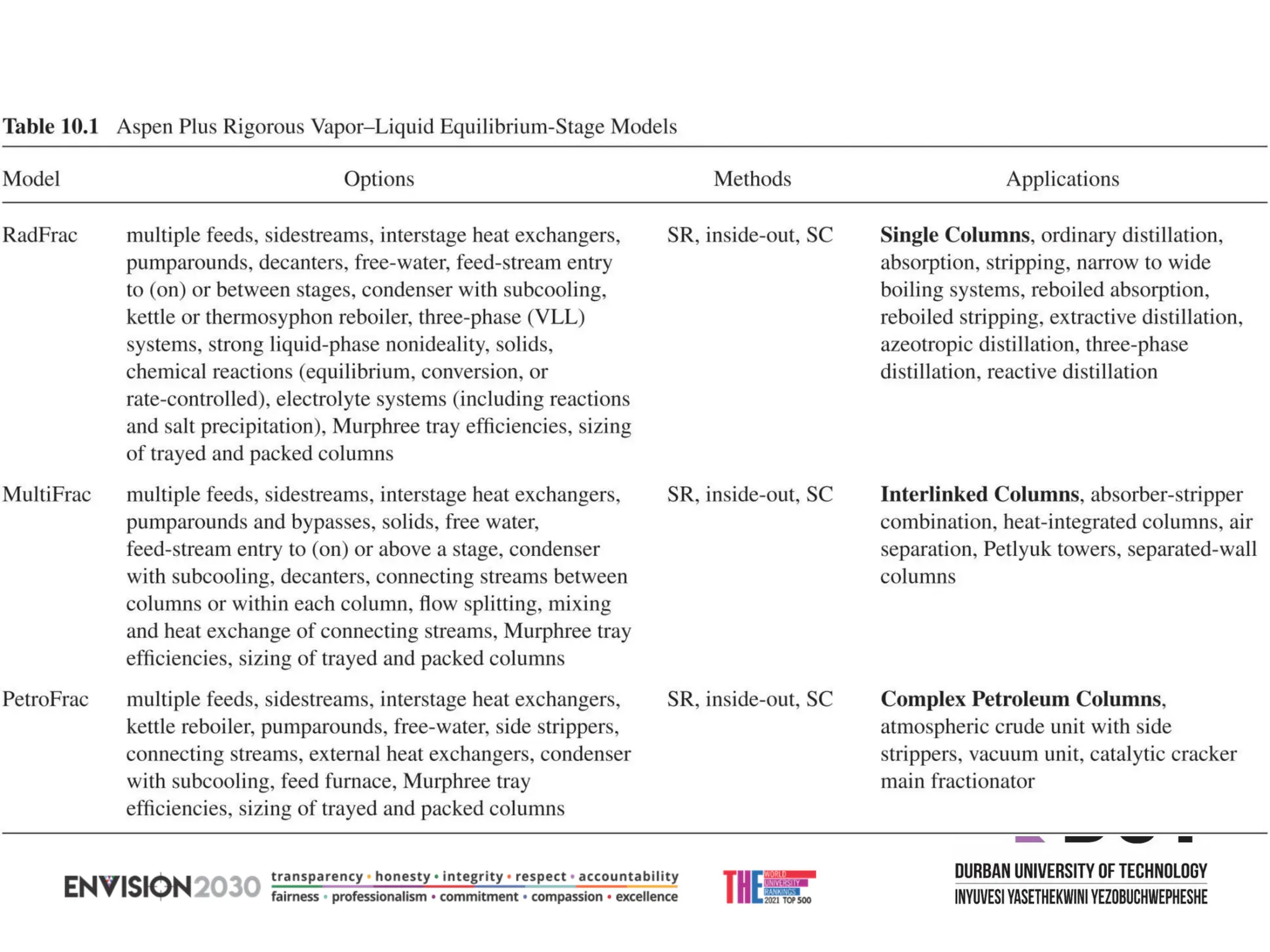
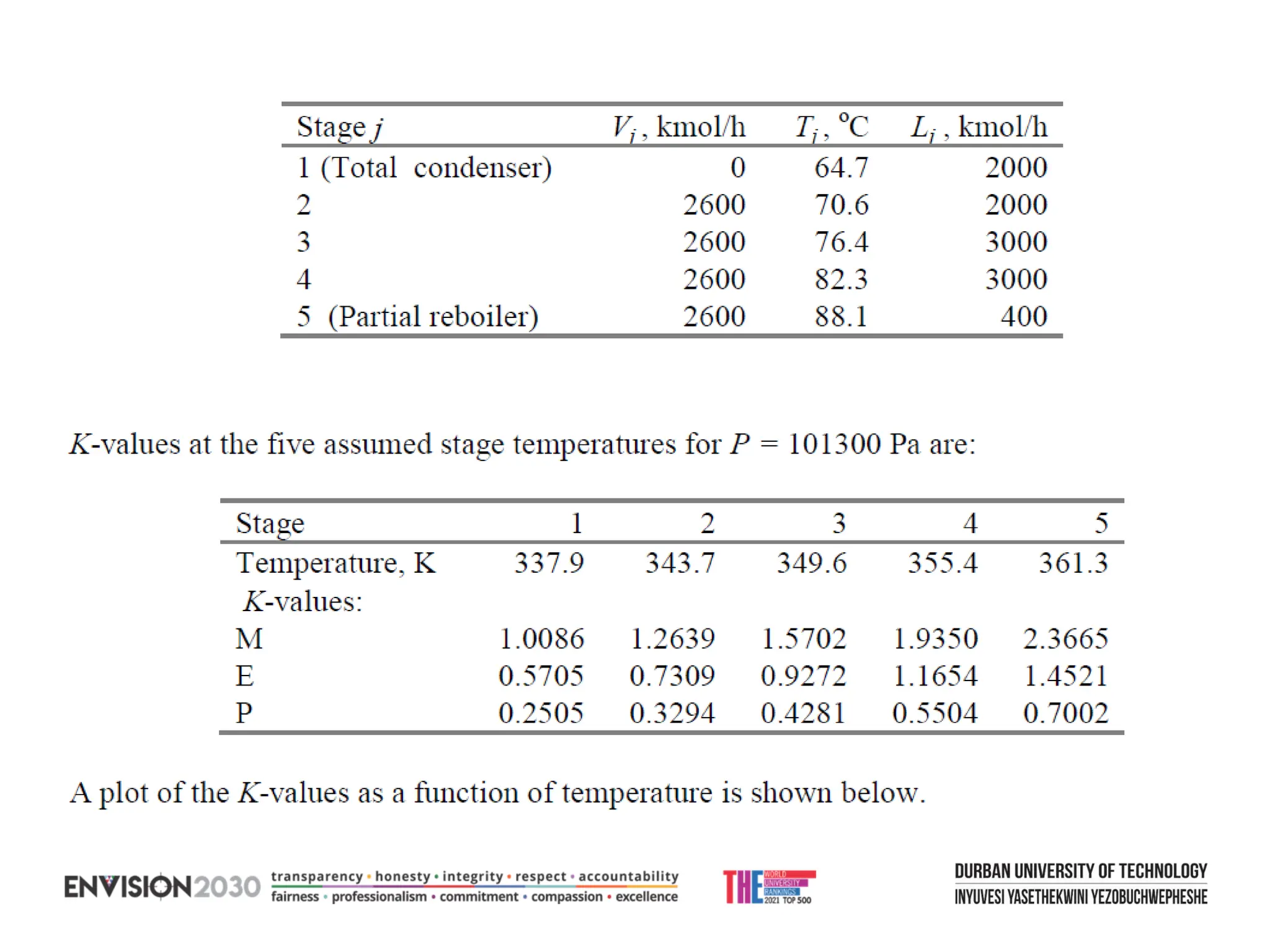
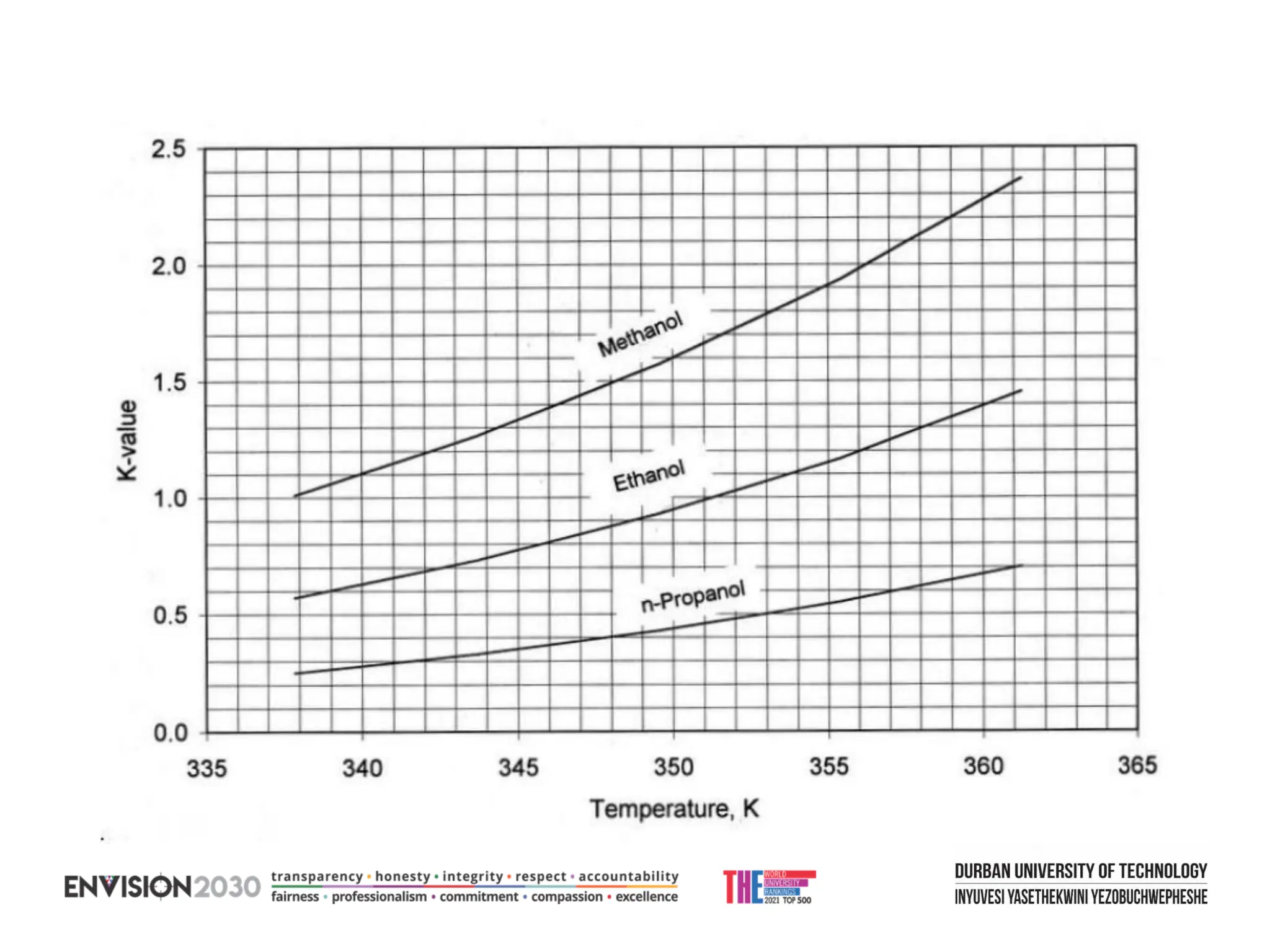
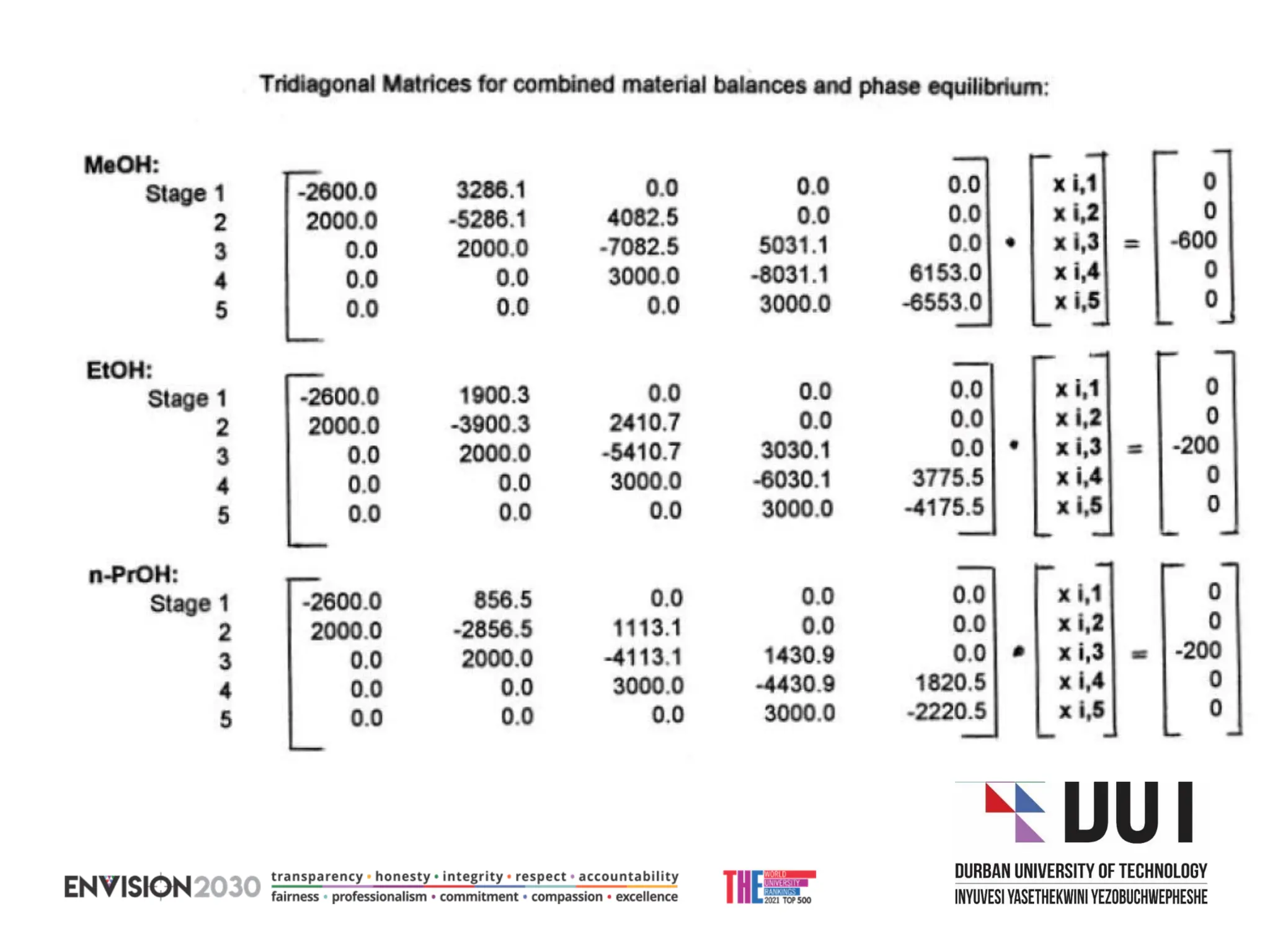
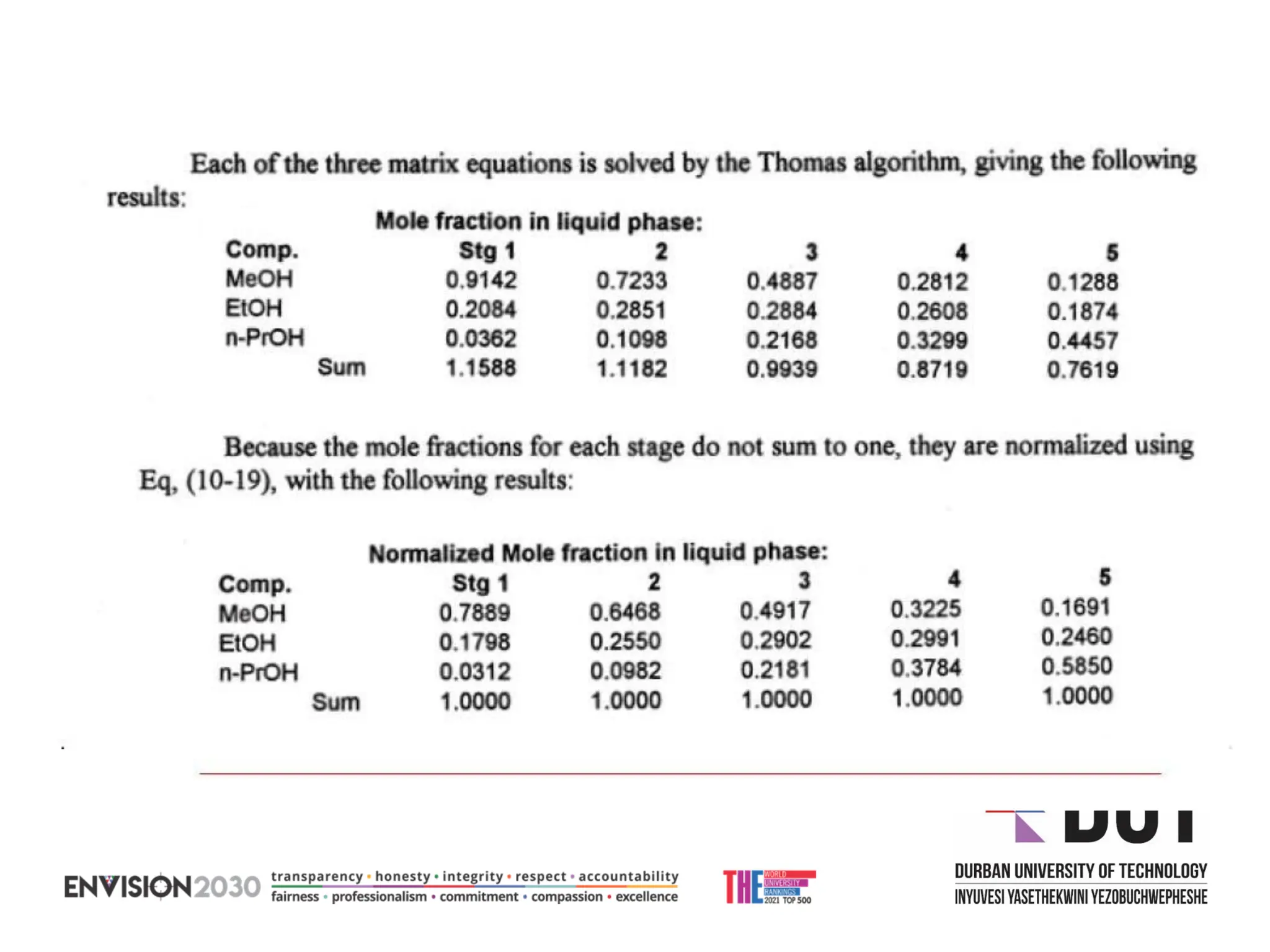
The document outlines lecture notes on separation technology, detailing the use of equilibrium-based methods for multicomponent separation processes like absorption, stripping, distillation, and extraction. It discusses mathematical modeling, solution procedures for nonlinear equations, and algorithms for calculating stage temperatures and compositions in process simulations. Additionally, the document contains information on assignments, test dates, and recommended textbooks for the course.

2. Dr E K Tetteh
Green Engineering Research Group
Department of Chemical Engineering
Steve Biko Campus , S4L1
*e-mail: emmanuelk@dut.ac.za
Cell +27-31-3732498
1
Lecture Note: Separation Technology (STEC101)
Computer-aided design and analysis
Equilibrium-Based Methods for Multicomponent

3. ❖ Library orientation: Consult the library for the following prescribed textbooks;
✓ Seader, J.D; Henley, E; Roper, J. 2011. Separation Process Principles Chemical and
Biochemical Operation, 3rd Ed, John Wiley and Sons, Inc
✓ McCabe, W. L; Smith, J. C; Harriot, P. 2005. Unit Operations of Chemical
Engineering, 7th Ed, McGraw-Hill Int.
✓ Coulson, J. M; Richardson, J. F. 2002. Chemical Engineering, Volume 2.
✓ Treybal, R. E. 1994, Mass Transfer Operations
✓ McCabe, W. L; Smith, J. C. 2006. Unit Operation for Chemical Engineering
✓ Foust, S. 1990. Principal of Unit Operation
❖ Test 2: 9th May, 2024 Time 17h00 -20h00
❖ Assignment Due: 17th May, 2024 Time 23h00 via Moodle submission

4. ➢ Equilibrium-Based Methods for Multicomponent
✓ Absorption
✓ Stripping
✓ Distillation
✓ Extraction
Separation Technologies :
➢ This chapter discusses the solution methods used in process simulators, with
applications to absorption, stripping, distillation, and liquid-liquid extraction.

5. ➢ The final design of multistage, multicomponent separation
equipment requires rigorous determination of temperatures,
pressures, stream flow rates, stream compositions, and heat-
transfer rates at each stage
by solving material balance, energy balance, and equilibrium
relations for each stage.
➢ Unfortunately, these relations consist of strongly interacting nonlinear algebraic
equations, where solution procedures are difficult and tedious. However, once the
procedures are programmed for a highspeed digital computer, solutions are usually
achieved rapidly
➢ Development of a mathematical model for an equilibrium stage for vapour–liquid
contacting
When collected together, the resulting equations form a counter-current cascade of stages,
which are called the MESH equations.

6. ✓ The number of strategies for solving these equations are used.
✓ All utilize an algorithm for solving a tridiagonal-matrix equation.
✓ The bubble-point (BP) method is efficient when the feed(s) to the cascade contain
components with a narrow boiling-point range.
✓ The sum-rates (SR) method is a better choice when the components cover a wide range
of volatilities.
✓ The BP and SR methods are relatively simple but are restricted to ideal and nearly ideal
mixtures and have limited allowable specifications.
✓ More flexible, complex methods, Newton–Raphson (NR) and insideout are required for
non-ideal systems and are widely available in process simulators

7. For any stage in a counter-current cascade,
assume (1) phase equilibrium is achieved
at each stage, (2) no chemical reactions
occur, and (3) entrainment of liquid drops
in vapour and occlusion of vapour bubbles
in liquid are negligible.
The figure represents such a stage for the
vapour–liquid case, where the stages are
numbered down from the top. The same
representation applies to liquid-liquid
extraction if liquid streams represent the
higher-density liquid phases and the
lower-density liquid phases are
represented by vapour stream
Theoretical Model For An Equilibrium Stage

8. Heat is often used in columns having
sidestreams, such as crude units. in
petroleum refineries to conserve energy
and balance column vapour loads.
Advanced models in process simulators
can handle pumps around.
THEORETICAL MODEL FOR AN EQUILIBRIUM
STAGE WITH PUMP AROUNDS

9. MESH EQUATIONS The equations are referred to as MESH equations, after Wang
and Henke

10. MESH EQUATIONS
The equations are referred to as MESH equations, after Wang and Henke

11. GENERAL COUNTERCURRENT
CASCADE OF N STAGES.
Early, pre-computer attempts to solve (10-1) to
(10-5) or Equivalent forms of these equations
resulted in the classical stage-by-stage,
equation-by-equation calculational procedures
of Lewis–Matheson in 1932 and Thiele Geddes
in 1933 based on equation tearing for solving
simple fractionators with one feed and two
products

12. ➢ Modern equation-tearing procedures are rapidly programmed and require minimal
computer memory.
➢ Although they can be applied to a wider variety of problems than the Thiele–Geddes
tearing procedure
➢ They are usually limited to the same choice of specified variables, including, most
importantly, the number of equilibrium stages and feed and product stage locations.
➢ Product purities, species recoveries, interstage flow rates and stage temperatures
are not specified
The strategy of mathematical solution
Equation-tearing procedures:

13. ➢ The key to the BP and SR tearing procedures is the tridiagonal matrix, which results
from a modified form of the M equations, (10-1), when they are torn from the other
equations by selecting Tj and Vj as the tear variables, leaving the modified M
equations linear in the unknown liquid mole fractions.
➢ This set of equations, one for each component, is solved by a modified
Gaussian–elimination algorithm due to Thomas as applied by Wang and Henke.
The modified M equations are obtained by substituting (10-2) into (10-1) to
eliminate y and by substituting (10-6) into (10-1) to eliminate L.
➢ Thus, equations for calculating y and L are partitioned from the other equations. The
result for each component, i, and each stage, j, is as follows, where the i subscripts
have been dropped from the B, C, and D terms.
Tridiagonal Matrix Algorithm

18. Bubble-Point (BP) Method for Distillation
✓ Frequently, distillation involves species that cover a relatively narrow range of K-values.
✓ It is referred to as the bubble-point (BP) method because a new set of stage temperatures is
computed during each iteration from the bubble-point equations.
✓ All equations are partitioned and solved sequentially except for the M equations (10-1),
which are solved separately for each component by the tridiagonal-matrix technique.
✓ Specifications are conditions and stage location of feeds, stage pressures, flow rates of side
streams (note that liquid distillate flow rate, if any, is designated as U1), heat-transfer rates
for all stages except stage 1 (condenser) and stage N (reboiler), total stages,
bubble-point reflux flow rate, and vapor distillate flow rate.
✓ The Wang–Henke algorithm is shown below:

20. Bubble-Point (BP) Method for Distillation
➢ To initiate the calculations, values of tear variables, Vj and Tj, are assumed.
Generally, it is sufficient to establish an initial set of Vj values based on constantmolar
interstage flows using the specified reflux, distillate, feed, and side stream
flows.
➢ Initial Tj values can be provided by computing the bubble-point temperature of an
estimated bottoms product and the dew-point temperature of an assumed distillate
product (or computing a bubble-point temperature if distillate is liquid, or a
temperature in between the dew point and bubble point if distillate is both vapor and
liquid), and then using linear interpolation for the other stage temperatures.
➢ To solve (10-12) for xi by the Thomas method, Ki,j values are required. When they
are composition-dependent, initial assumptions for all xi,j and yi,j values are also
needed, unless ideal K-values are employed initially. For each iteration, the computed
set of xi,j values for each stage are not likely to satisfy the summation constraint
given by (10-4).
➢ Although not mentioned by Wang and Henke, it is advisable to normalize the set of
computed xi,j values by the relation

21. ➢ At the other extreme, bubble-point calculations can be sensitive to composition for
a binary mixture containing one component with a high K-value that changes little
with temperature and a second component with a low K-value that
changes rapidly with temperature. Such a mixture is methane and n-butane at 400
psia.
➢ The effect on bubble-point temperature of small quantities of methane dissolved in
liquid n-butane is very large:

34. Sum-Rates (SR) Method for Absorption and Stripping
The species in most absorbers and strippers cover a widerange of volatility. Hence, the BP
method of solving the MESH equations fails because bubble-point temperature calculations
are too sensitive to liquid-phase composition, and the stage energy balance
This sum-rates (SR) method was further developed in conjunction with the tridiagonal-
matrix formulation for the modified M equations by Burningham and Otto . Figure shows the
Burningham–Otto SR algorithm

40. Tutorials :`1

51. Green Engineering Research Group
Department of Chemical Engineering
Steve Biko Campus , S4L1
e-mail: emmanuelk@dut.ac.za
Cell +27-31-3732498