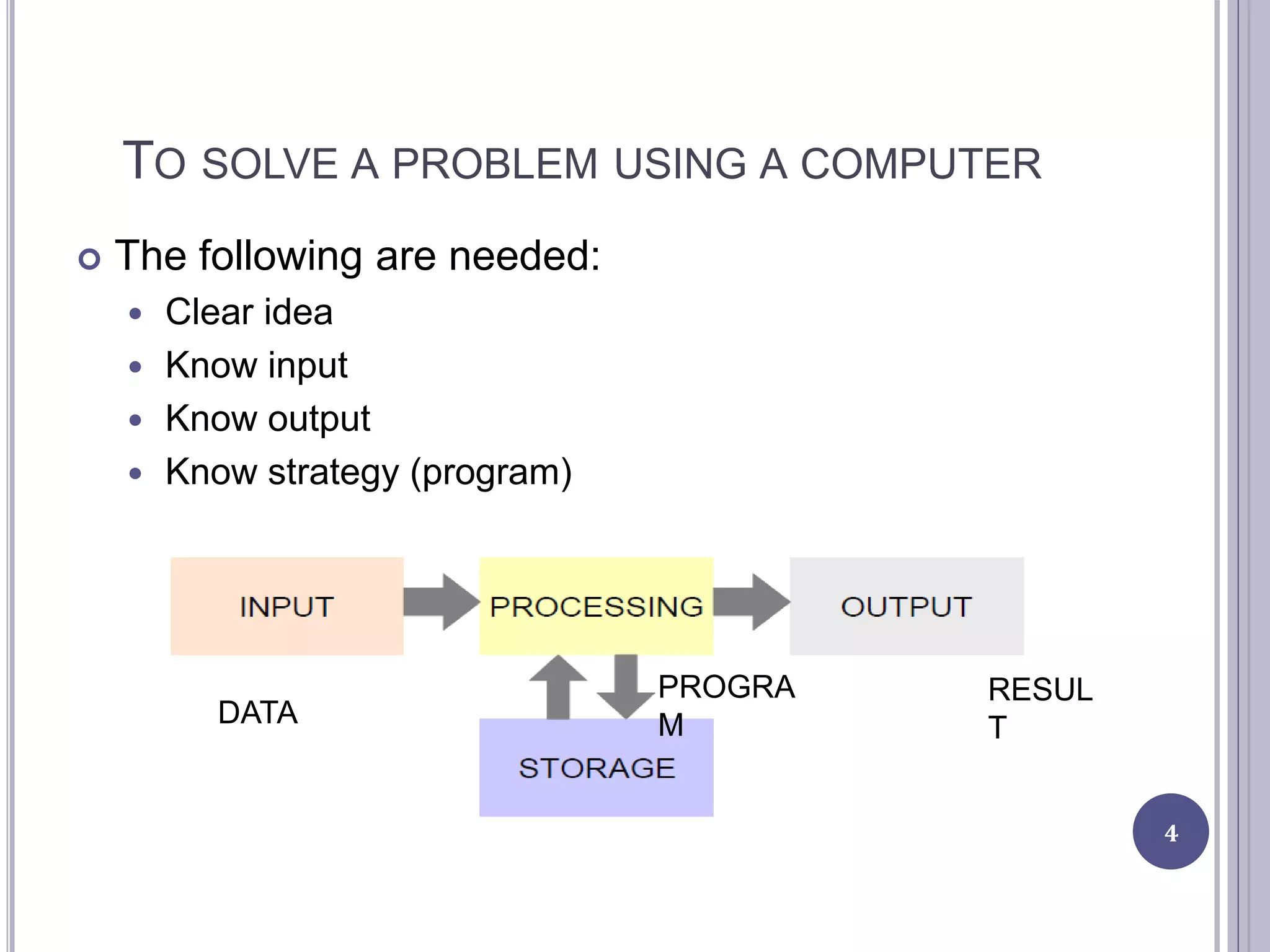
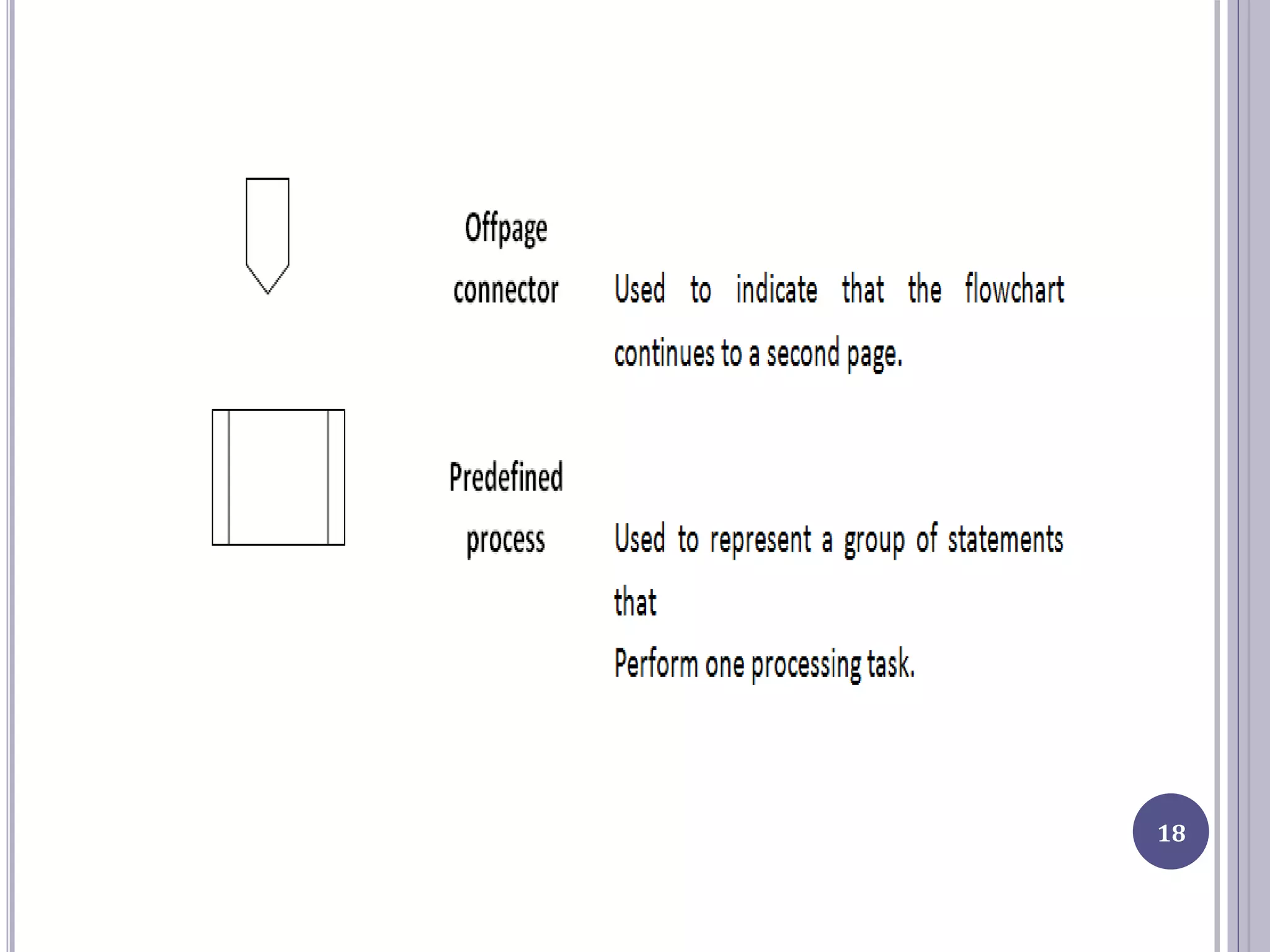
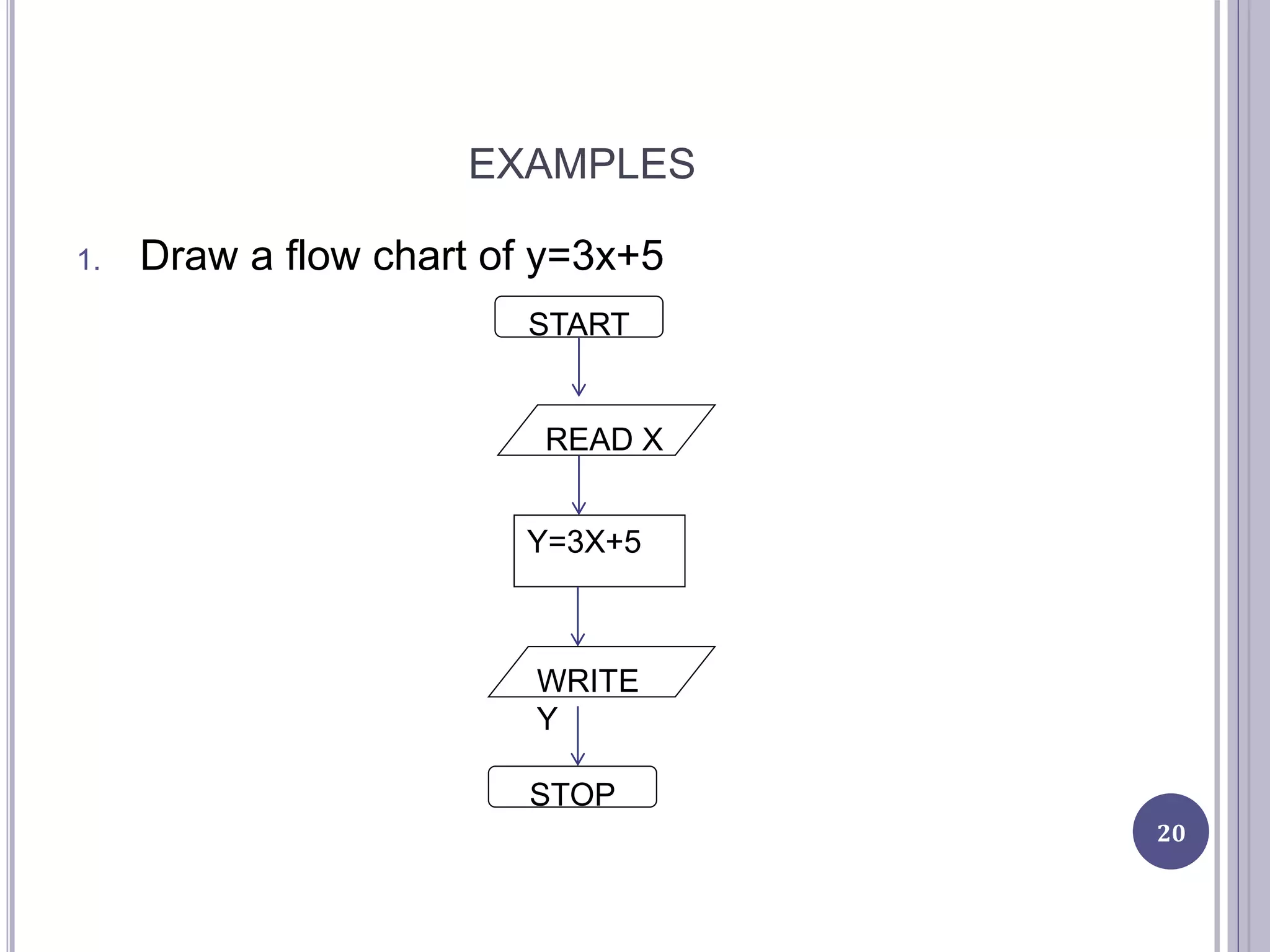
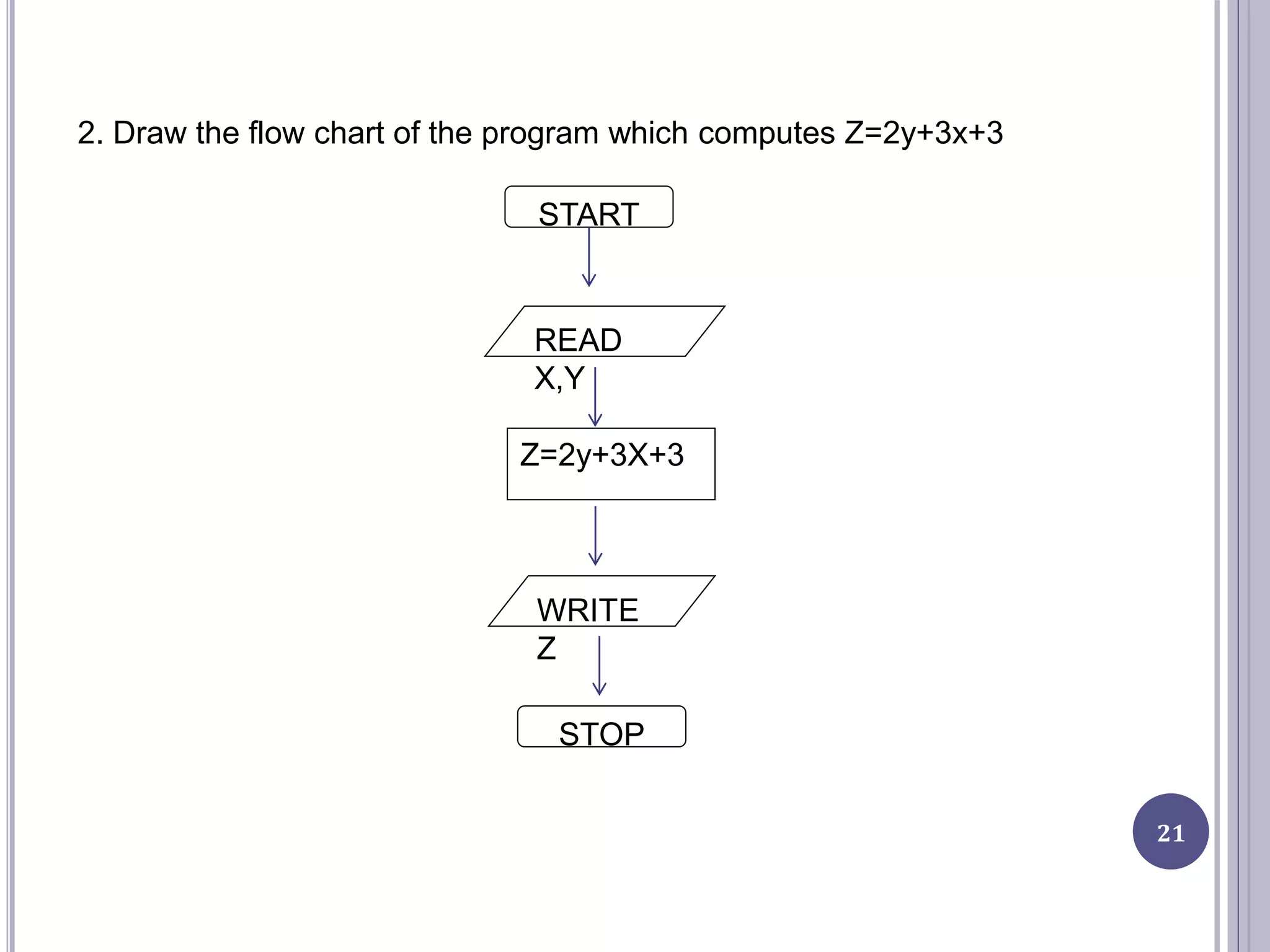
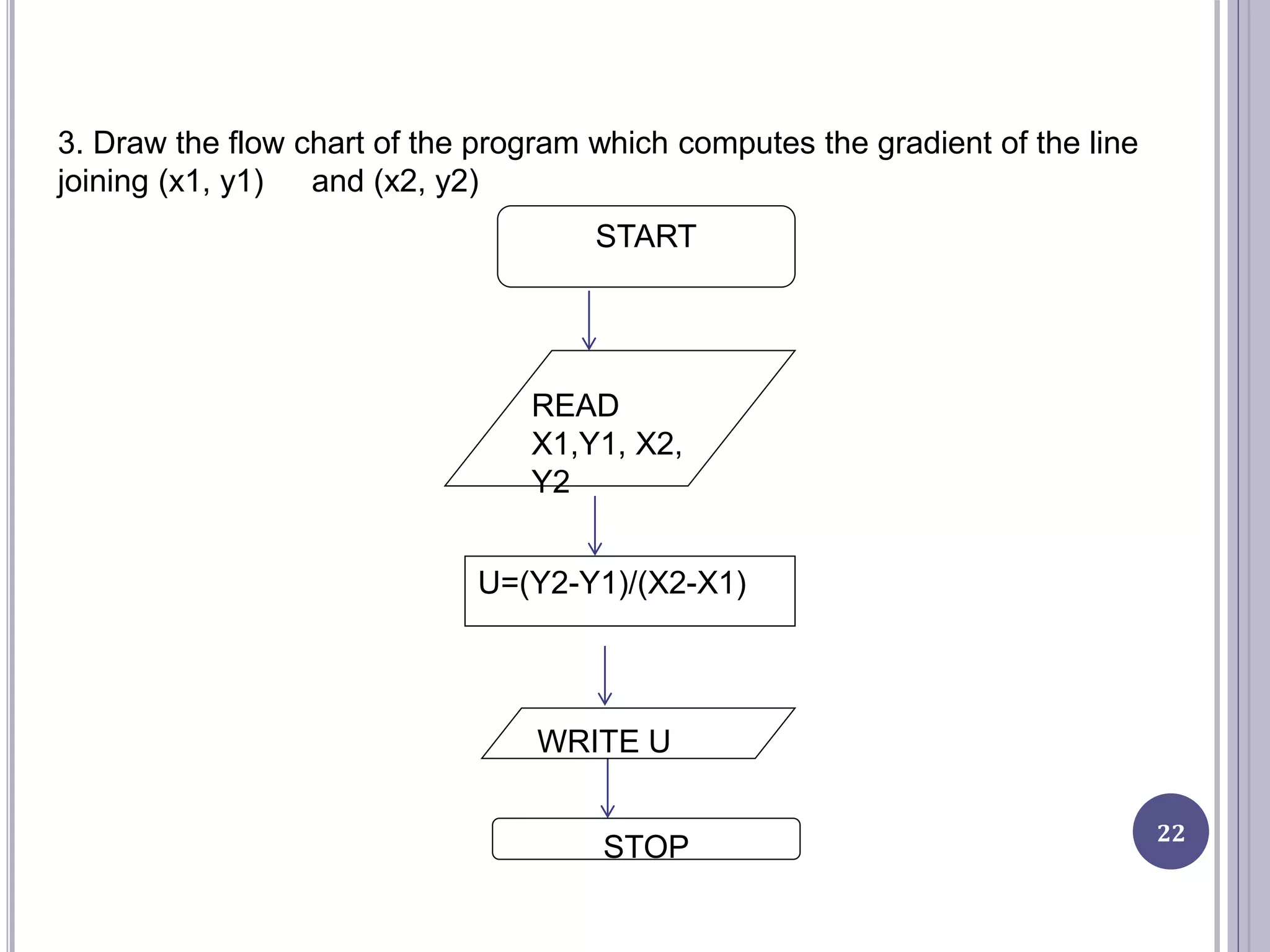
This document provides an introduction to computer science and programming concepts such as algorithms, flowcharts, and pseudocode. It discusses how to solve problems with computers by writing programs, and the steps involved in the program development cycle of analyzing a problem, designing an algorithm, implementing the program, and testing it. The document also explains algorithms, flowcharts which diagram algorithms using standard symbols, and pseudocode which describes algorithms in plain English. Examples of algorithms and flowcharts are provided.

1. INTRODUCTION TOCOMPUTER SCIENCE
CSC 1302
LECTURE 5
Department of Maths and Computer-
Science
Faculty of Natural and Applied Science
BY
UMAR DANJUMA MAIWADA

2. OBJECTIVES
 Solving problem with computer
 Algorithm
 Flow chart
2

3. SOLVING PROBLEMS WITH COMPUTER
 Computer works by obeying a sequence of
instructions, which constitutes a program.
 To solve a problem with computer, there
must be a program to solve it.
 A program needs careful planning, good
organization.
 A problem can be solved by writing a
program in one of many programming
languages, such as C++, Java, Pascal, and
Python.
3

4. TO SOLVE A PROBLEM USING A COMPUTER
 The following are needed:
 Clear idea
 Know input
 Know output
 Know strategy (program)
4
DATA
PROGRA
M
RESUL
T

5. STEPS INVOLVED IN SOLVING A PROBLEM
 Understand the problem.
 Breaking the problem into manageable pieces.
 Designing a solution.
 Considering alternatives to the solution and refining
the solution.
 Implementing the solution.
 Testing the solution and fixing any problems that
exist.
5

6. PROGRAM DEVELOPMENT CYCLE
 Analyse: Define the problem - Have a clear idea of
what data (or input) are given and the relationship
between the input and the desired output.
 Design: Plan the solution to the problem - logical
sequence of precise steps that solve the problem.
Such a sequence of steps is called an algorithm.
 Choose the interface: Select the objects - how the
input will be obtained and how the output will be
displayed. Then create objects to receive the input
and display the output.
 Code: Translate the algorithm into a programming
language - Coding is the technical word for writing
the program. During this stage, the program is written
in programming language of choice and entered into
6

7. 7
o Test and debug: Locate and remove any errors
in the program - Testing is the process of finding
errors in a program, and debugging is the
process of correcting errors that are found.
many errors occurring due to typing mistakes,
flaws in the algorithm, or incorrect usages of the
programming language rules only can be
uncovered and corrected by careful detective
work.
o Complete the documentation: Organize all the
material that describes the program -
Documentation is intended to allow another
person or the programmer at a later date, to
understand the program. Internal documentation
consists of statements in the program that are
not executed, but point out the purposes of
various parts of the program.

8. ALGORITHMS
 Algorithm is a set of instructions which is taken in
order to lead to a solution.
 Algorithm consist of a sequence of operation for the
particular solution of the stated problem.
 It does not have to be written in computer
language.
 Algorithms have a definite beginning and a definite
end, and a finite number of steps.

9. PROPERTIES OF ALGORITHM
 Must be able to determine after a finite number of
steps e.g listing all counting numbers is not an
algorithm
 The steps must be clearly stated
 The input (Data) must be clear and well defined
 Given correct input, the algorithm must give correct
output (GIGO).
 An algorithm must be efficient in terms of time
consumption and computer memory space.
9

10. HOW TO DEVELOP A PROGRAM
 Problem formulation
 Design the algorithm
 Converting the algorithm into computer program
 Debugging and testing of the program
10

11. QUALITIES OF A GOOD ALGORITHM
 Inputs and outputs should be defined precisely.
 Each steps in algorithm should be clear and
unambiguous.
 Algorithm should be most effective among many
different ways to solve a problem.
 An algorithm shouldn't have computer code.
Instead, the algorithm should be written in such a
way that, it can be used in similar programming
languages
11

12. EXAMPLE OF A SIMPLE ADDITION ALGORITHM
 Step 1: Start
 Step 2: Declare variables num1, num2 and sum.
 Step 3: Read values num1 and num2.
 Step 4: Add num1 and num2 and assign the result
to sum.
 sum←num1+num2
 Step 5: Display sum
 Step 6: Stop
12

13. GIVEN VALUES OF THE VARIABLE P, Q, R,
COMPUTE THE VALUE OF H=6P+8Q-R THEN
WRITE ALGORITHM
 Get values of p, q, and r
 Compute H=6.p+8.q-r
 Report the resulting value of H
 End
13

14. WRITE THE ALGORITHM FOR THE PROGRAM WHEN TAKES IN VALUES
OF A, B, C, D, E AND Y AND COMPUTE X= A.Y.Y.Y.Y + B.Y.Y.Y +
C.Y.Y.D.Y+E
 Get values of A, B, C, D, E, Y
 Compute X=A.Y.Y.Y.Y+B.Y.Y.Y+C.Y.Y-D.Y+E
 Report the resulting value of X
 End
14

15. FLOW CHART
 Flow chart is a diagrammatic representation of an
algorithm or a program.
 A flow chart is a type of diagram representing a
process using different symbols containing
information about steps or a sequence of events.
 Flowcharts are helpful for:
 Aiding understanding of relationships among different
process steps
 Collecting data about a particular process
 Helping with decision making
 Measuring the performance of a process
 Depicting the structure of a process
 Tracking the process flow
 Highlighting important steps and eliminating the
unnecessary steps
 A flowchart consists of special geometric symbols
15

16. 16
The main advantage of using a flowchart
to plan a task is that it provides a pictorial
representation of the task, which makes
the logic easier to follow. We can clearly
see every step and how each step is
connected to the next.
The major disadvantage with flowcharts
is that when a program is very large, the
flowcharts may continue for many pages,
making them difficult to follow and modify.

17. A TABLE OF THE FLOWCHART SYMBOLS ADOPTED BY THE
AMERICAN NATIONAL STANDARDS INSTITUTE (ANSI)
FOLLOWS.
17

18. 18

19. GENERAL RULES FOR FLOW CHARTING
 1. All boxes of the flowchart are connected with Arrows. (Not
lines)
 2. Flowchart symbols have an entry point on the top of the
symbol with no other entry points. The exit point for all
flowchart symbols is on the bottom except for the Decision
symbol.
 3. The Decision symbol has two exit points; these can be on
the sides or the bottom and one side.
 4. Generally a flowchart will flow from top to bottom. However,
an upward flow can be shown as long as it does not exceed 3
symbols.
 5. Connectors are used to connect breaks in the flowchart.
Examples are:
 • From one page to another page.
 • From the bottom of the page to the top of the same page.
 • An upward flow of more than 3 symbols
 6. Subroutines and Interrupt programs have their own and
independent flowcharts.
19

20. EXAMPLES
1. Draw a flow chart of y=3x+5
20
START
READ X
Y=3X+5
WRITE
Y
STOP

21. 21
2. Draw the flow chart of the program which computes Z=2y+3x+3
START
READ
X,Y
Z=2y+3X+3
WRITE
Z
STOP

22. 22
3. Draw the flow chart of the program which computes the gradient of the line
joining (x1, y1) and (x2, y2)
START
READ
X1,Y1, X2,
Y2
U=(Y2-Y1)/(X2-X1)
WRITE U
STOP

23. PSEUDOCODE
 Pseudocode is an abbreviated version of actual
computer code (hence, pseudocode). The
geometric symbols used in flowcharts are replaced
by English-like statements that outline the process.
 Pseudocode allows the programmer to focus on the
steps required to solve a problem rather than on
how to use the computer language.
 Pseudocode has several advantages. It is compact
and probably will not extend for many pages as
flowcharts commonly do.
23

24. PROGRAMMING TOOLS
 A programming tool may be any software program
or utility that aids software developers or
programmers in creating, editing, debugging,
maintaining and/or performing any programming or
development-specific task.
 Programming tools were initially designed to
support or complement programming languages by
providing the functionality and features these
languages did not have.
 Compilers, linkers, assemblers, disassemblers,
load testers, performance analysts, GUI
development tools and code editors are also all
forms of programming tools.
24

25. QUESTIONS???
THANK YOU FOR YOUR ATTENTION
25