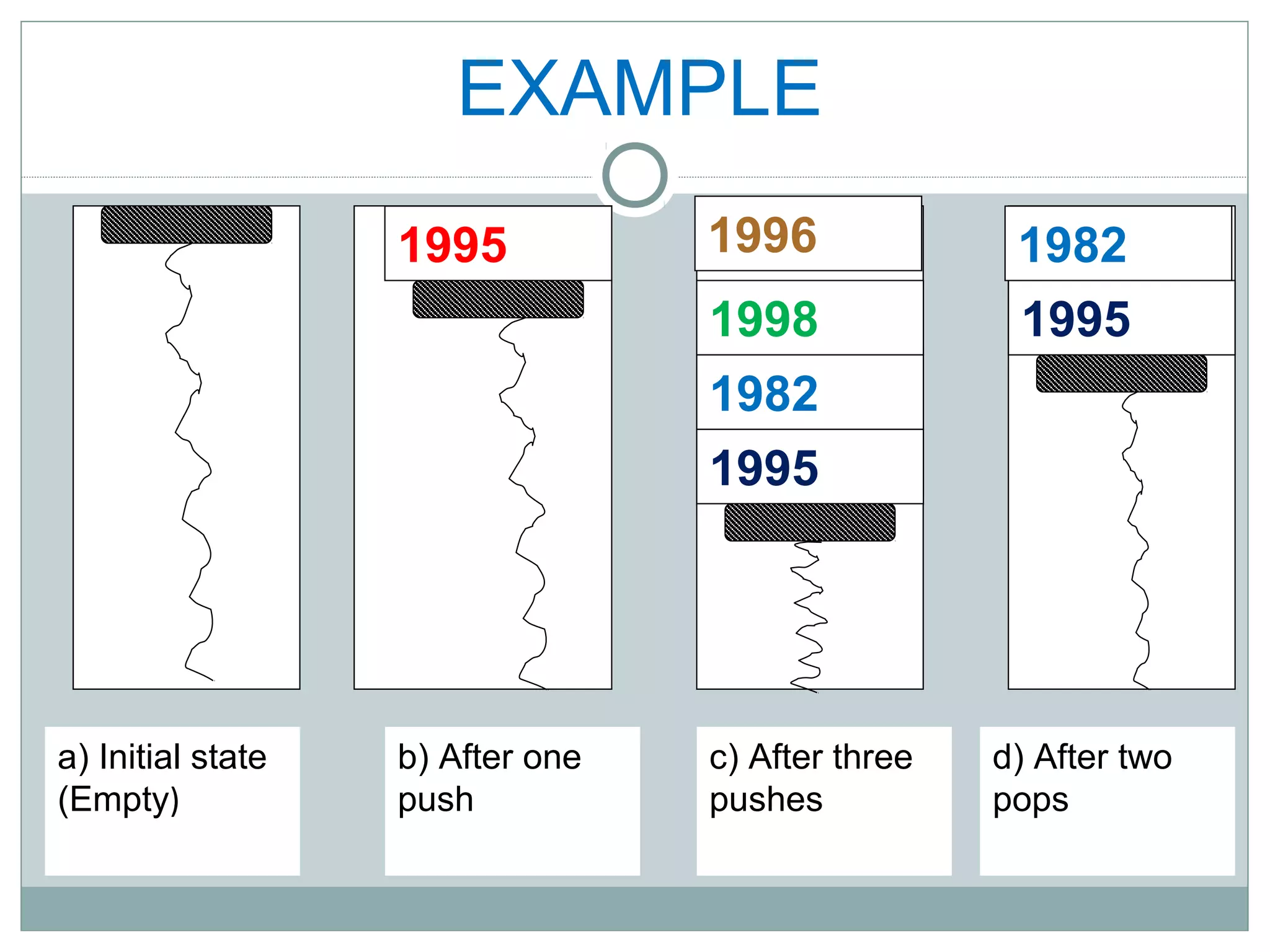
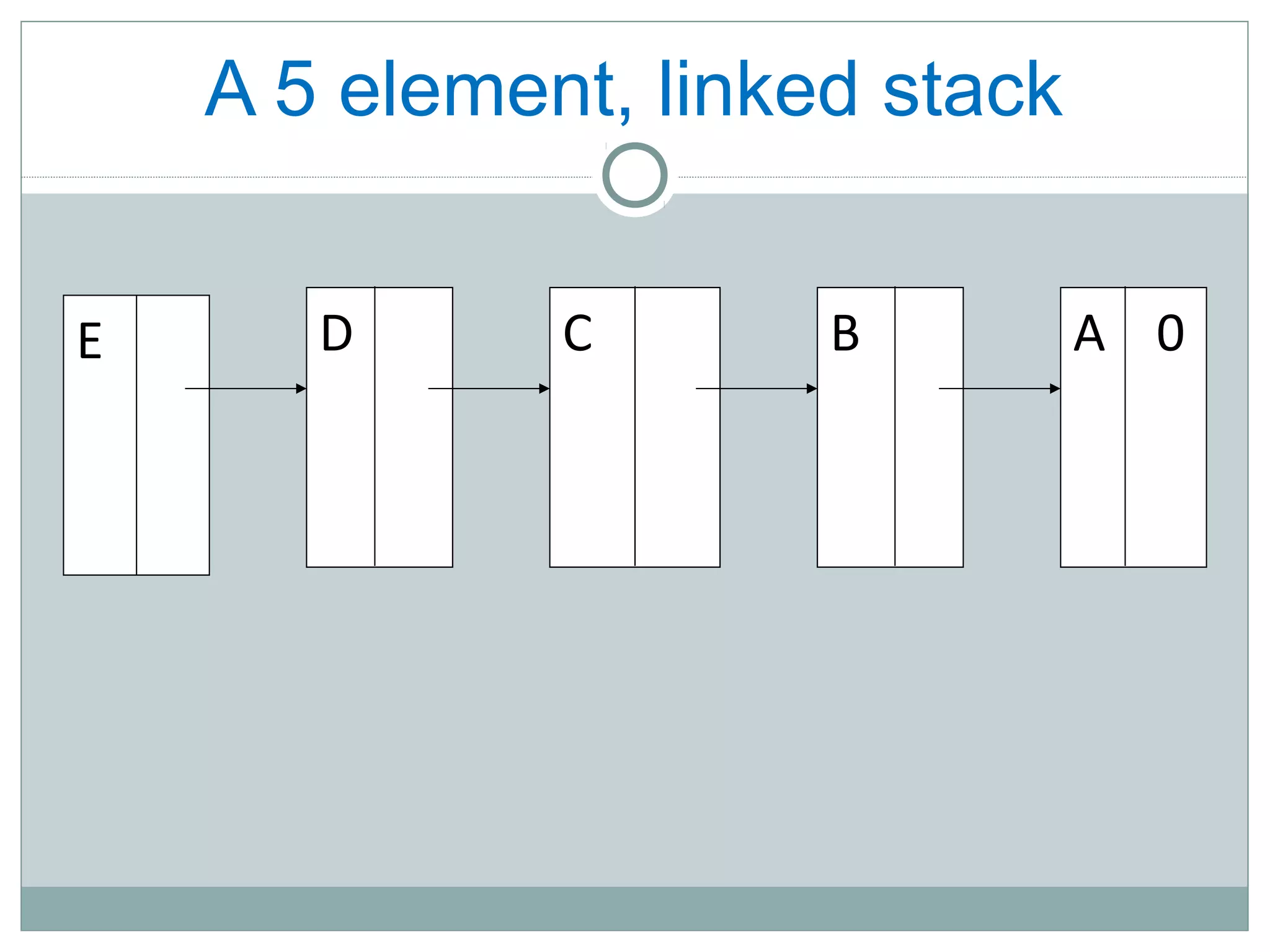
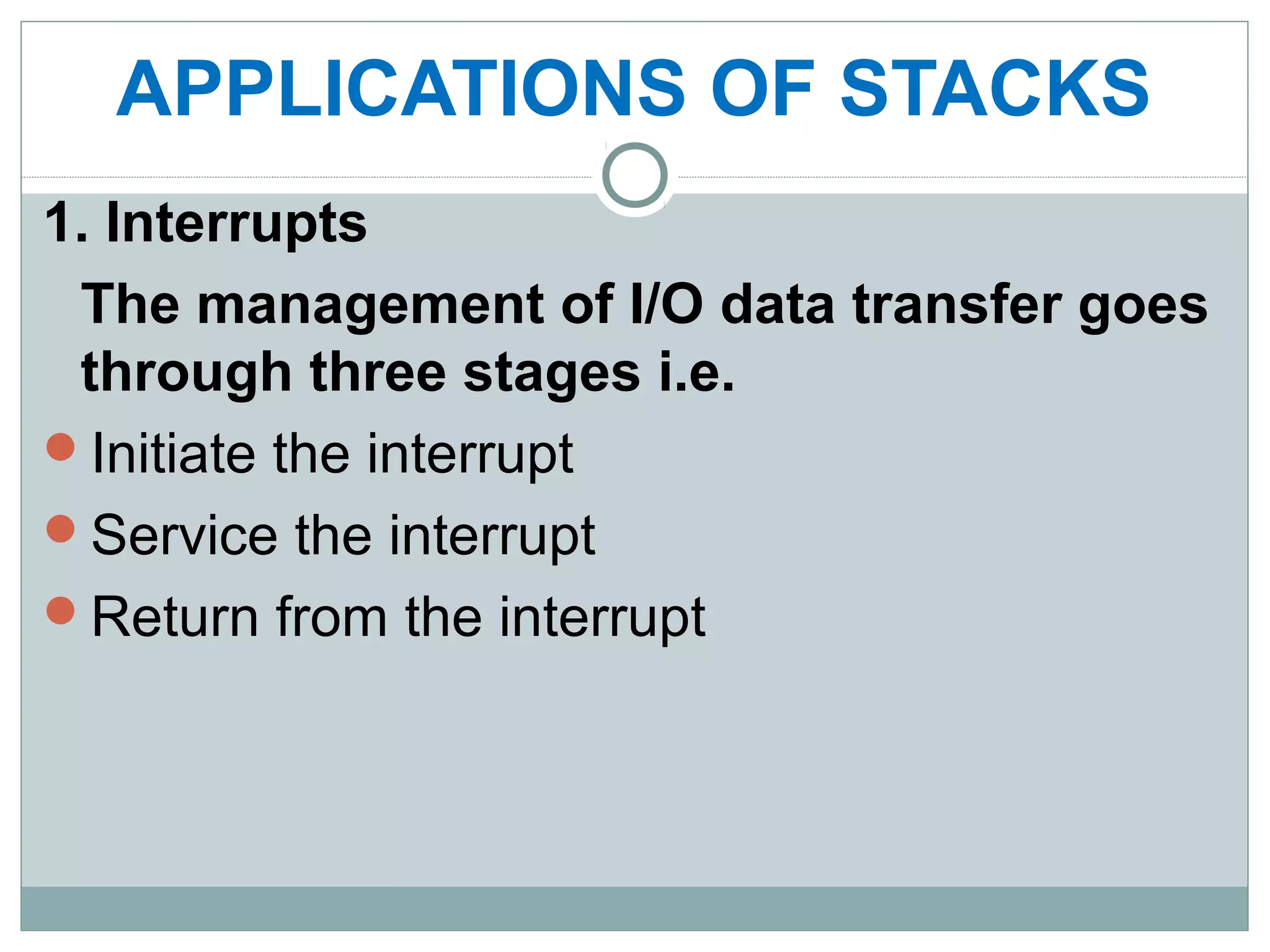
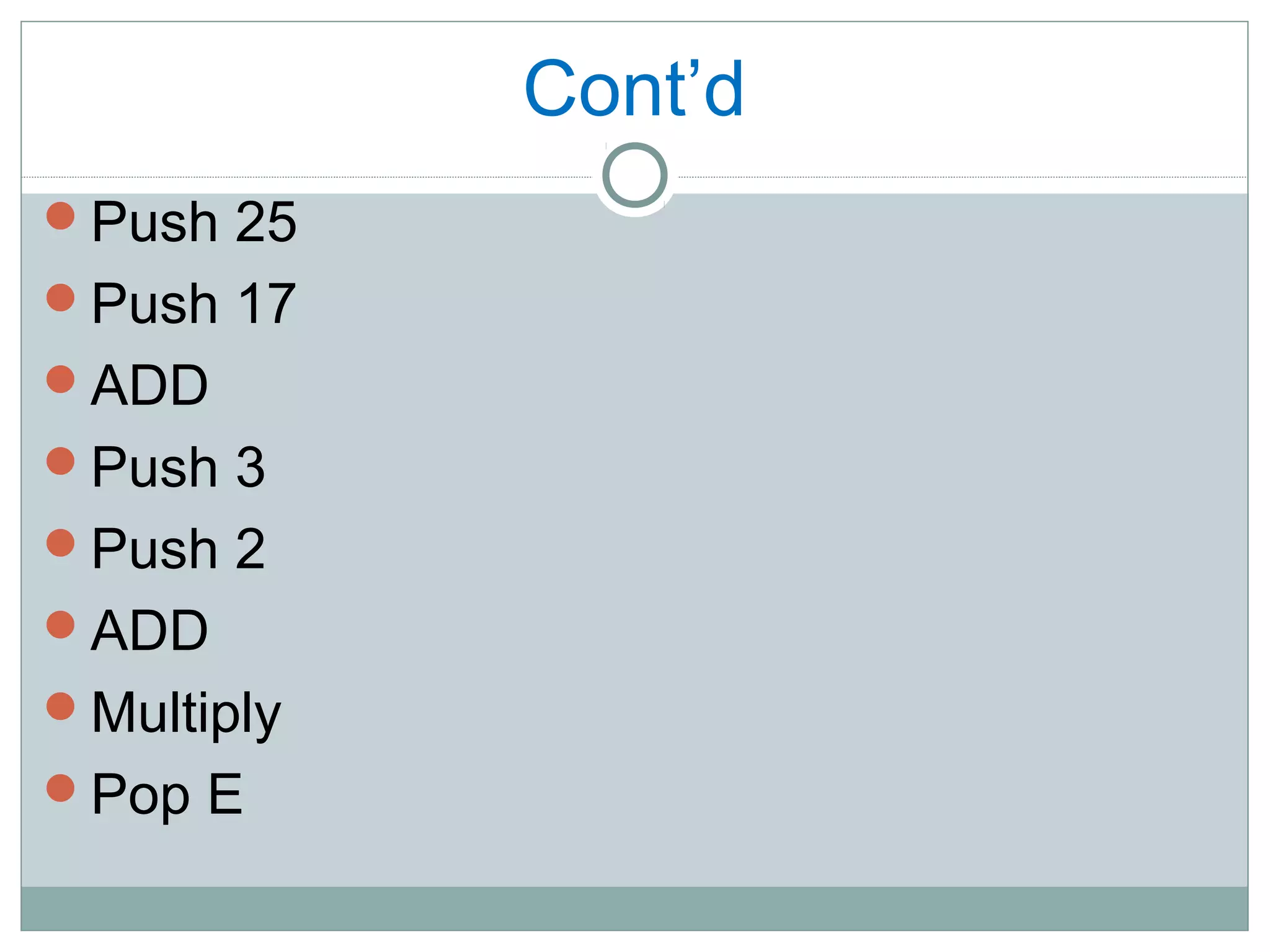
A stack is a linear data structure that follows the last-in, first-out (LIFO) principle. Elements can only be inserted or removed from one end, called the top. Common stack operations include push, which adds an element to the top, and pop, which removes the top element. Stacks have many applications, such as evaluating mathematical expressions, interrupt handling in computing, and temporary storage in stack machines. They can be implemented using either arrays or linked lists.

1. STACKS- INTRODUCTION
Data structures are organized grouping of data
items, treated as a unit regarded as data
aggregates e.g. arrays, trees, stacks, queues.
 Data structures allow a programmer to create
data types by grouping together data of more
primitive types.

2. DEFINITIONS
• A stack is an ordered list of elements in which
insertions and deletions are made at one end
called the top.
• The point of access of a stack is called the top.
• A stack is linear list whose elements may be
created & deleted only in a last in first out
order.

3. DEFINITIONS
• A stack is a linear list for which all insertions
& deletions and usually all accesses are
made at one end of the list.
• A stack is an ADT that is a storage
mechanism which is defined by the
operations performed on it & not at all by the
specific manner in which it is implemented.

4. DEFINITIONS
A stack allows access to only one data item:
the last item inserted. If you remove this item,
then you can access the next-to-last item
inserted, and so on.
A stack is also known as a pushdown list or a
LIFO (Last In First Out) list.

5. DEFINITIONS
• A Push Operation
It appends one new item to the top of the stack
or to the top of a non-full stack.
• A Pop Operation
It removes or deletes the top item from the
stack.

6. DEFINITIONS
• Stack Pointer
• It contains the address of the top of the stack.
• If an item is appended to or deleted from the
stack, the pointer is incremented or
decremented respectively to contain the
address of the new top of the stack.

7. DEFINITIONS
• Stack base
• It contains the address of the bottom location in
the received block. If an attempt is made to pop
when the stack is empty an error is reported.
• Stack limit
• Contains the address of the other end of the
received block. If an attempt is made to push
when the block is fully utilized for the stack an
error is reported.

8. Characteristics of Stacks
It Mainly Uses The Principle Of Last In
First Out
Can add and delete without disturbing the
arrangement

9. EXAMPLE
1995 1996
1995
1982
1998
1995
1982
a) Initial state
(Empty)
d) After two
pops
c) After three
pushes
b) After one
push

10. Use of Links (or Pointers)
A Stack can be represented by using links or
pointers.
Two nodes with two fields, possibly called
DATA and LINK can represent a stack.
 (A node is a collection of data and link
information).
The data field of each node contains an item
in the stack and the corresponding link field
points to the node containing the next item in
the stack

11. Use of Links (or Pointers)
The linked field of the last node is zero for
we assume that all nodes have an address
greater than zero.
For example, a stack with the items A, B, C,
D, E inserted in that order, would look as in
the figure below:

12. A 5 element, linked stack
E D C B A 0

13. Cont’d
The variable STACK points to the topmost node (the
last item inserted) in the list.
The empty stack is represented by setting STACK =
0.
The use of links to represent a stack requires more
storage than the sequential array.

14. Array Implementation of Stacks
A stack can be implemented with an array and
an integer.
The integer tos (Top of stack) provides the
array index of the top element of the stack.
Thus if tos is –1, the stack is empty.
 The array implementation keeps the bottom of
the stack at the beginning of the array.
It grows toward the end of the array.

15. Cont’d
The array implementation has one serious
drawback: you must know the max. no. of items
in your collection when you create it.
This presents problems in programs in which
this max. no. cannot be predicted accurately
when the program starts up.
A linked list can be used to overcome this
limitation.

16. Linked List Implementation of Stacks
The linked list is a very flexible dynamic data
structure: items may be added to it or deleted
from it at will.
The stack interface can be implemented by
using a linked list in which the top of the stack is
represented by the first item in the list

17. Used in linear data structure simply because they
figure so prominently in systems programming
especially in compiler design.
 Storage management in recursive programming & to
implement inherently recursive routines.
 Used for processing nested program structures for
example bracketed arithmetic/logical expressions;
programs with block structures; statements with
matching delimiters as; If, Then, Else, End.
USES OF STACKS

18. APPLICATIONS OF STACKS
1. Interrupts
The management of I/O data transfer goes
through three stages i.e.
Initiate the interrupt
Service the interrupt
Return from the interrupt

19. 2) Stack as a Temporary Storage
Some computer use stack instead of general
purpose registers to store temporary values
during computation
These computations are called stack
machines or zero address machines.
The h/w recalls the source operands on the
stack which would be popped & then supplied
to the ALU & the results of the addition would
be pushed onto the stack

20. Cont’d
To perform an addition, the h/w would execute
two pops & a push
Two pops would remove the two sources
operands from the stack, the add would
compute the sum & push would replace the
results back on the stack.
Most calculators use stacks, Example:
Evaluate: (A+B)(C+D) and store the results in
E: where A is 25; B is 17; C is 3; D is 2

21. Cont’d
Push 25
Push 17
ADD
Push 3
Push 2
ADD
Multiply
Pop E

22. 3) Data Type Conversion
Every instruction should be provided with
source operands of the data type that the
instruction requires i.e. ADD requires operands
that are two complement integers.
Example 2+3=
A stack is used in keeping track of data type of
each of the values that one is working with

23. LIMITATION
The concept of the stack being a LIFO structure
removing & adding items from the stack
requires a strict order, which is serially.
Insertions & deletions can be performed only
from the one position, which is at the top.
This implies that the sequence of Pushes of A,
B, C, D. has to be eventually followed by the
Pops of D,C,B and A.
The stack limit or the default values may not be
enough & this will result in overflows.

24. LIMITATION
Overflows are conditions that occur when one
tries to push a value onto a stack and there is
no available space.
The user should always check therefore that
the stack is not full before inserting an item.
Often a stack full condition will signal that more
storage needs to be allocated and the program
reruns.

25. LIMITATION
A programmer requires prior knowledge or
proper presentation & a good understanding
of the program when deciding or the number
of stack for optimum performance.

26. CONCLUSION
In a nutshell stacks are form of an ADT that is
a storage mechanism which is defined by the
operations performed on it & not at all by the
specific manner in which it is implemented &
are composed of pointer, top, base & peek
button.
They simply aid in writing an algorithm.