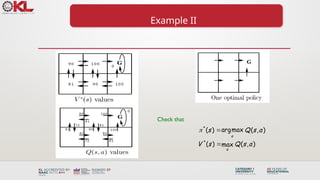
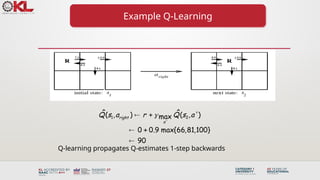
El documento presenta un curso sobre aprendizaje automático no supervisado centrado en clustering jerárquico y técnicas de estandarización de datos. Además, se describe el proceso de Q-learning, un enfoque de aprendizaje por refuerzo que permite a los agentes aprender a partir de la experiencia sin necesidad de un modelo del mundo. Se mencionan diversas aplicaciones del aprendizaje por refuerzo, como la automatización industrial, planificación estratégica y control de tráfico.