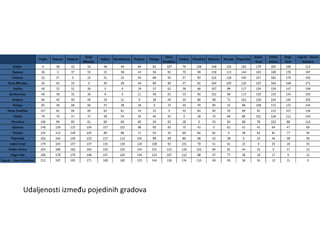
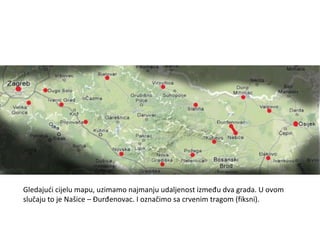
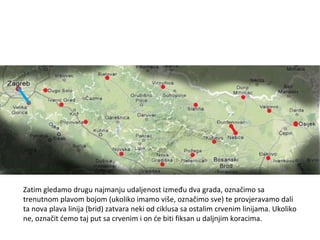
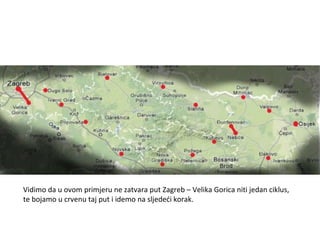
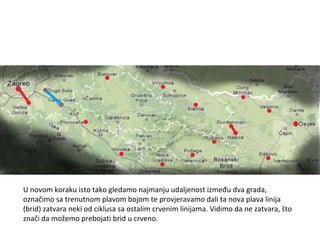
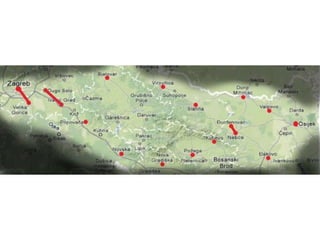
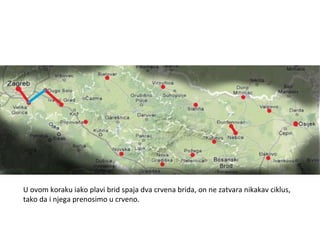
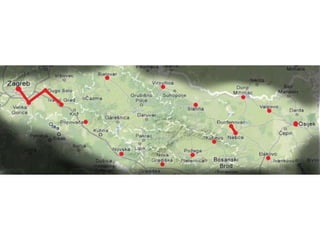
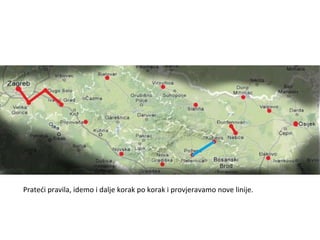
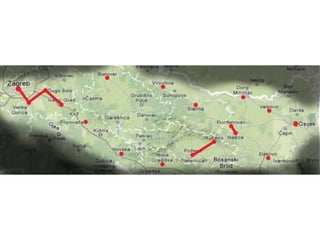
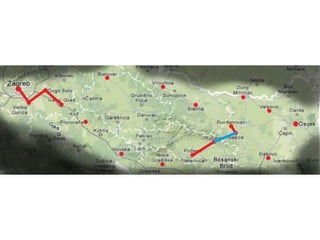
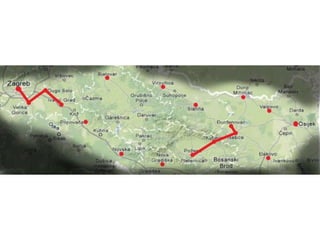
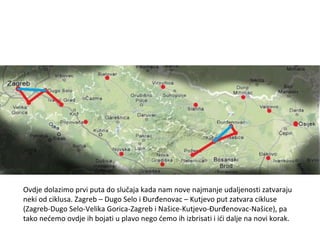
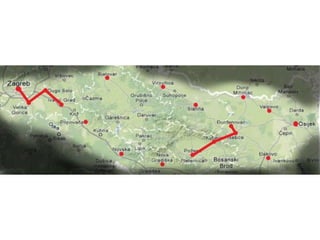
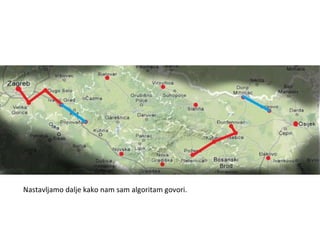
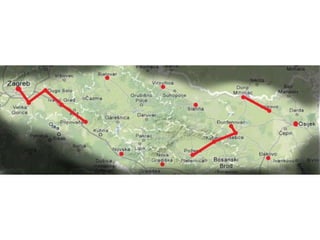
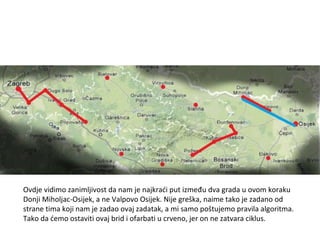
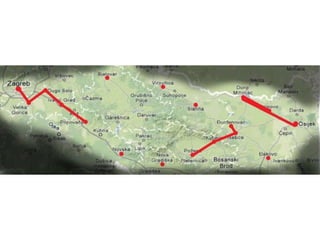
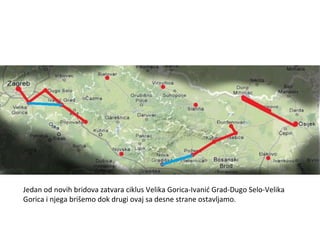
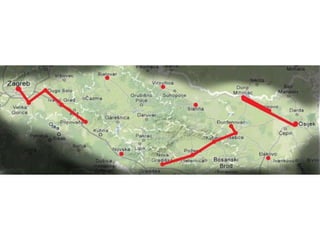
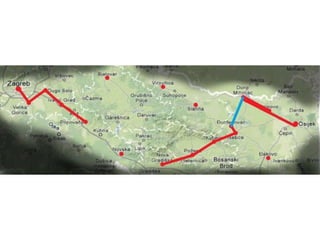
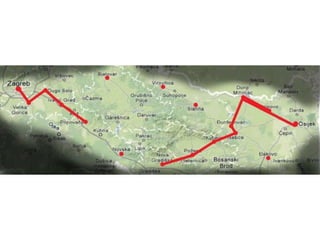
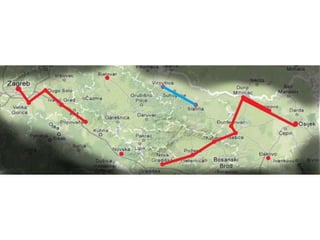
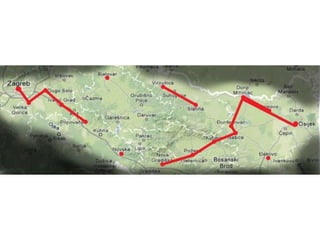
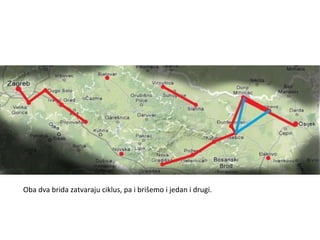
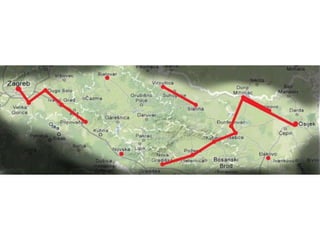
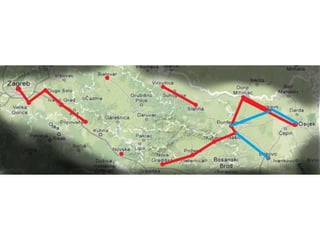
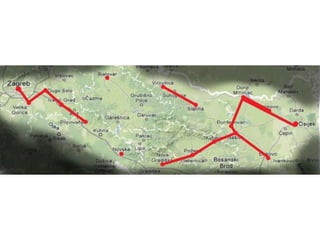
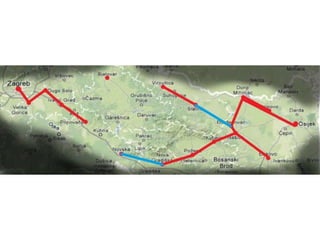
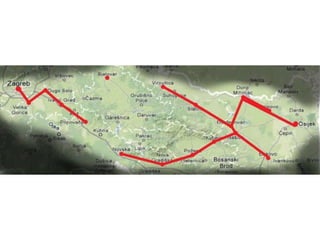
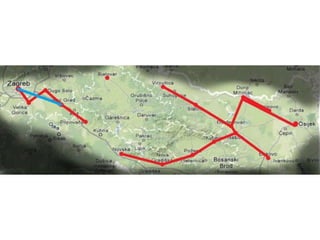
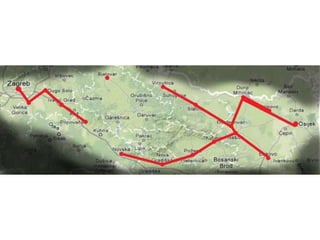
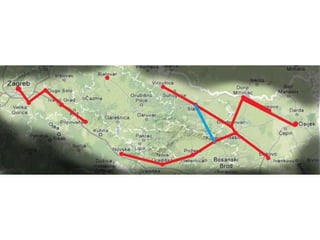
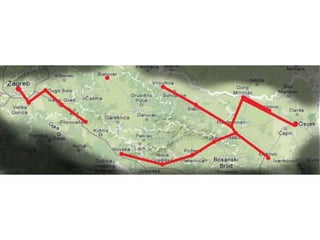
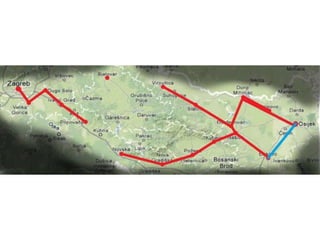
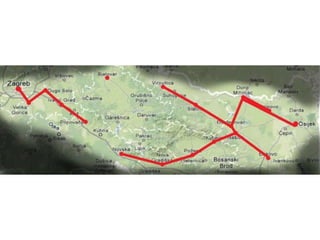
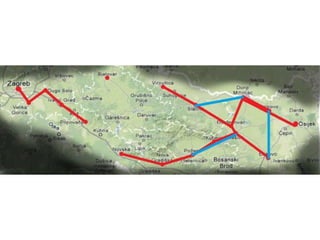
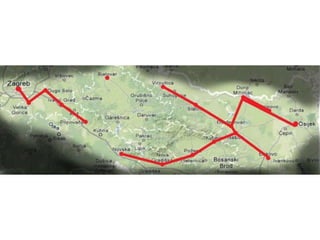
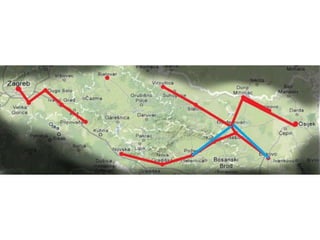
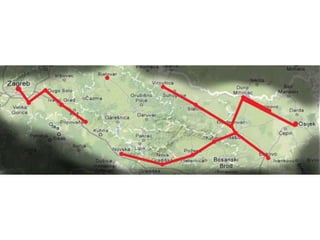
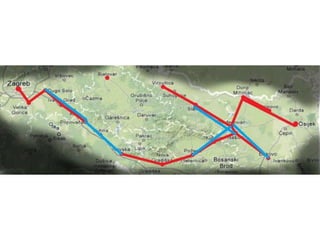
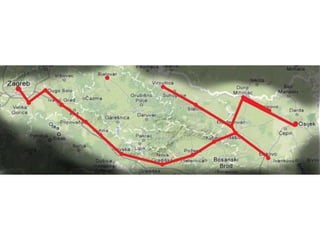
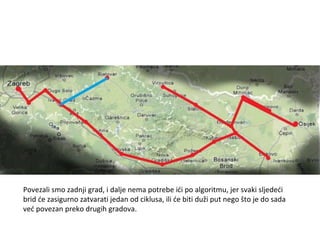
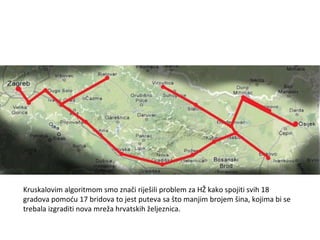
Projekat revitalizacije hrvatskih željeznica koristi Kruskalov algoritam za dizajniranje nove pruge koja povezuje 18 gradova s minimalnim brojem šina. Proces uključuje odabir najkraćih udaljenosti između gradova i provjeru zatvaraju li novi putevi cikluse, čime se osigurava efikasna povezanost. Na kraju, projekt definira 17 puteva koji će optimizirati željezničku mrežu.

1. Korištenje Kruskalovog algoritma Budu ć i da Hrvatske željeznice ve ć godinama posluju s velikim gubicima, a pruga između gradova prikazanih Slikom je dotrajala, trebate pomo ć i upravi HŽ-a. Naime, vaš je zadatak da isprojektirate novu prugu koja ć e povezivati sve gradove označene na Slici i pobrojane u Tablici 1, u kojoj se nalaze i udaljenosti između pojedinih gradova. Kod projektiranja pruge morate paziti da utrošiti minimalnu količina šina. Ne mora biti povezan svaki grad sa svakim, ved npr. iz Slatine se u Osijek može dodi kroz Đurđenovac. Svi gradovi koji su označeni crvenim kružićem na Slici moraju biti uključeni u mrežu.

2. Karta gradova za koje je potrebno riješiti problem.

3. Udaljenosti između pojedinih gradova

4. Gledajući cijelu mapu, uzimamo najmanju udaljenost između dva grada. U ovom slučaju to je Našice – Đurđenovac. I označimo sa crvenim tragom (fiksni).

5. Zatim gledamo drugu najmanju udaljenost između dva grada, označimo sa trenutnom plavom bojom (ukoliko imamo više, označimo sve) te provjeravamo dali ta nova plava linija (brid) zatvara neki od ciklusa sa ostalim crvenim linijama. Ukoliko ne, označit ćemo taj put sa crvenim i on će biti fiksan u daljnjim koracima.

6. Vidimo da u ovom primjeru ne zatvara put Zagreb – Velika Gorica niti jedan ciklus, te bojamo u crvenu taj put i idemo na sljedeći korak.

7. U novom koraku isto tako gledamo najmanju udaljenost između dva grada, označimo sa trenutnom plavom bojom te provjeravamo dali ta nova plava linija (brid) zatvara neki od ciklusa sa ostalim crvenim linijama. Vidimo da ne zatvara, što znači da možemo prebojati brid u crveno.

9. U ovom koraku iako plavi brid spaja dva crvena brida, on ne zatvara nikakav ciklus, tako da i njega prenosimo u crveno.

11. Prateći pravila, idemo i dalje korak po korak i provjeravamo nove linije.

15. Ovdje dolazimo prvi puta do slučaja kada nam nove najmanje udaljenosti zatvaraju neki od ciklusa. Zagreb – Dugo Selo i Đurđenovac – Kutjevo put zatvara cikluse (Zagreb-Dugo Selo-Velika Gorica-Zagreb i Našice-Kutjevo-Đurđenovac-Našice), pa tako nećemo ovdje ih bojati u plavo nego ćemo ih izbrisati i ići dalje na novi korak.

17. Nastavljamo dalje kako nam sam algoritam govori.

19. Ovdje vidimo zanimljivost da nam je najkraći put između dva grada u ovom koraku Donji Miholjac-Osijek, a ne Valpovo Osijek. Nije greška, naime tako je zadano od strane tima koji nam je zadao ovaj zadatak, a mi samo poštujemo pravila algoritma. Tako da ćemo ostaviti ovaj brid i ofarbati u crveno, jer on ne zatvara ciklus.

21. Jedan od novih bridova zatvara ciklus Velika Gorica-Ivanić Grad-Dugo Selo-Velika Gorica i njega brišemo dok drugi ovaj sa desne strane ostavljamo.

27. Oba dva brida zatvaraju ciklus, pa i brišemo i jedan i drugi.

45. Povezali smo zadnji grad, i dalje nema potrebe ići po algoritmu, jer svaki sljedeći brid će zasigurno zatvarati jedan od ciklusa, ili će biti duži put nego što je do sada već povezan preko drugih gradova.

46. Kruskalovim algoritmom smo znači riješili problem za HŽ kako spojiti svih 18 gradova pomoću 17 bridova to jest puteva sa što manjim brojem šina, kojima bi se trebala izgraditi nova mreža hrvatskih željeznica.