Download as PDF, PPTX
Uploaded bySangwoo Mo
Introduction to Diffusion Models
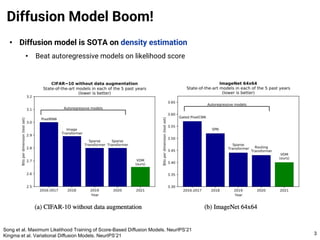
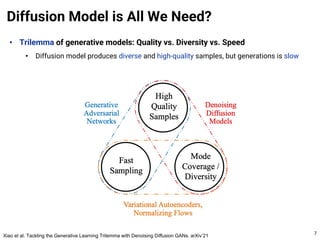
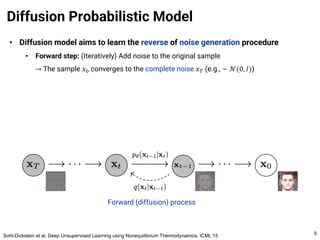
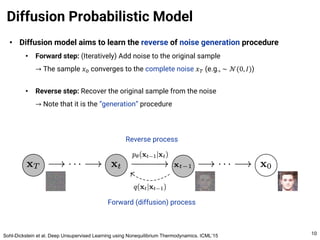
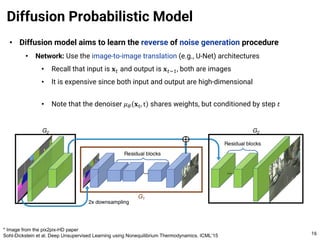
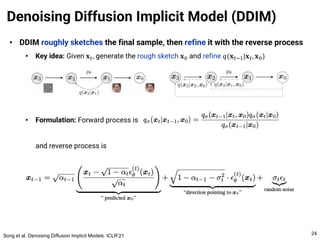
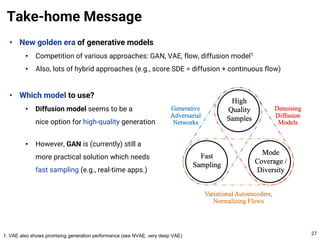
The document provides an introduction to diffusion models. It discusses that diffusion models have achieved state-of-the-art performance in image generation, density estimation, and image editing. Specifically, it covers the Denoising Diffusion Probabilistic Model (DDPM) which reparametrizes the reverse distributions of diffusion models to be more efficient. It also discusses the Denoising Diffusion Implicit Model (DDIM) which generates rough sketches of images and then refines them, significantly reducing the number of sampling steps needed compared to DDPM. In summary, diffusion models have emerged as a highly effective approach for generative modeling tasks.
More Related Content
Similar to Introduction to Diffusion Models
Introduction to Diffusion Models
- 1. Introduction to DiffusionModels 2022.01.03. KAIST ALIN-LAB Sangwoo Mo 1
- 2. • Diffusion modelis SOTA on image generation • Beat BigGAN and StyleGAN on high-resolution images Diffusion Model Boom! 2 Dhariwal & Nichol. Diffusion Models Beat GANs on Image Synthesis. NeurIPS’21
- 3. • Diffusion modelis SOTA on density estimation • Beat autoregressive models on likelihood score Diffusion Model Boom! 3 Song et al. Maximum Likelihood Training of Score-Based Diffusion Models. NeurIPS’21 Kingma et al. Variational Diffusion Models. NeurIPS’21
- 4. • Diffusion modelis useful for image editing • Editing = Rough scribble + diffusion (i.e., naturalization) • Scribbled images are unseen for GANs, but diffusion models still can denoise them Diffusion Model Boom! 4 Meng et al. SDEdit: Image Synthesis and Editing with Stochastic Differential Equations. arXiv’21
- 5. • Diffusion modelis useful for image editing • Also can be combined with vision-and-language model Diffusion Model Boom! 5 Nichol et al. GLIDE: Towards Photorealistic Image Generation and Editing with Text-Guided Diffusion Models. arXiv’21
- 6. • Diffusion modelis also effective for non-visual domains • Continuous domains like speech, and even for discrete domains like text Diffusion Model Boom! 6 Kong et al. DiffWave: A Versatile Diffusion Model for Audio Synthesis. ICLR’21 Austin et al. Structured Denoising Diffusion Models in Discrete State-Spaces. NeurIPS’21
- 7. • Trilemma ofgenerative models: Quality vs. Diversity vs. Speed • Diffusion model produces diverse and high-quality samples, but generations is slow Diffusion Model is All We Need? 7 Xiao et al. Tackling the Generative Learning Trilemma with Denoising Diffusion GANs. arXiv’21
- 8. • Today’s content •Diffusion Probabilistic Model – ICML’15 • Denoising Diffusion Probabilistic Model (DDPM) – NeurIPS’20 • Improve quality & diversity of diffusion model • Denoising Diffusion Implicit Model (DDIM) – ICLR’21 • Improve generation speed of diffusion model • Not covering • Relation of diffusion model and score matching • Extension to stochastic differential equation • There are lots of new interesting works (see NeurIPS’21, ICLR’22) Outline 8 Score SDE: Song et al. Score-Based Generative Modeling through Stochastic Differential Equations. ICLR’21 → See Score SDE (ICLR’21)
- 9. • Diffusion modelaims to learn the reverse of noise generation procedure • Forward step: (Iteratively) Add noise to the original sample → The sample 𝑥! converges to the complete noise 𝑥" (e.g., ∼ 𝒩(0, 𝐼)) Diffusion Probabilistic Model 9 Sohl-Dickstein et al. Deep Unsupervised Learning using Nonequilibrium Thermodynamics. ICML’15 Forward (diffusion) process
- 10. • Diffusion modelaims to learn the reverse of noise generation procedure • Forward step: (Iteratively) Add noise to the original sample → The sample 𝑥! converges to the complete noise 𝑥" (e.g., ∼ 𝒩(0, 𝐼)) • Reverse step: Recover the original sample from the noise → Note that it is the “generation” procedure Diffusion Probabilistic Model 10 Sohl-Dickstein et al. Deep Unsupervised Learning using Nonequilibrium Thermodynamics. ICML’15 Reverse process Forward (diffusion) process
- 11. • Diffusion modelaims to learn the reverse of noise generation procedure • Forward step: (Iteratively) Add noise to the original sample → Technically, it is a product of conditional noise distributions 𝑞(𝐱#|𝐱#$%) • Usually, the parameters 𝛽# are fixed (one can jointly learn, but not beneficial) • Noise annealing (i.e., reducing noise scale 𝛽# < 𝛽#$%) is crucial to the performance Diffusion Probabilistic Model 11 Sohl-Dickstein et al. Deep Unsupervised Learning using Nonequilibrium Thermodynamics. ICML’15
- 12. • Diffusion modelaims to learn the reverse of noise generation procedure • Forward step: (Iteratively) Add noise to the original sample → Technically, it is a product of conditional noise distributions 𝑞(𝐱#|𝐱#$%) • Reverse step: Recover the original sample from the noise → It is also a product of conditional (de)noise distributions 𝑝&(𝐱#'%|𝐱#) • Use the learned parameters: denoiser 𝝁& (main part) and randomness 𝚺& Diffusion Probabilistic Model 12 Sohl-Dickstein et al. Deep Unsupervised Learning using Nonequilibrium Thermodynamics. ICML’15
- 13. • Diffusion modelaims to learn the reverse of noise generation procedure • Forward step: (Iteratively) Add noise to the original sample Reverse step: Recover the original sample from the noise • Training: Minimize variational lower bound of the model 𝑝&(𝐱!) Diffusion Probabilistic Model 13 Sohl-Dickstein et al. Deep Unsupervised Learning using Nonequilibrium Thermodynamics. ICML’15
- 14. • Diffusion modelaims to learn the reverse of noise generation procedure • Forward step: (Iteratively) Add noise to the original sample Reverse step: Recover the original sample from the noise • Training: Minimize variational lower bound of the model 𝑝& 𝐱! → It can be decomposed to the step-wise losses (for each step 𝑡) Diffusion Probabilistic Model 14 Sohl-Dickstein et al. Deep Unsupervised Learning using Nonequilibrium Thermodynamics. ICML’15
- 15. • Diffusion modelaims to learn the reverse of noise generation procedure • Training: Minimize variational lower bound of the model 𝑝& 𝐱! → It can be decomposed to the step-wise losses (for each step 𝑡) • Here, the true reverse step 𝑞(𝐱#$%|𝐱#, 𝐱!) can be computed as a closed form of 𝛽# • Note that we only define the true forward step 𝑞(𝐱#|𝐱#$%) • Since all distributions above are Gaussian, the KL divergences are tractable Diffusion Probabilistic Model 15 Sohl-Dickstein et al. Deep Unsupervised Learning using Nonequilibrium Thermodynamics. ICML’15
- 16. • Diffusion modelaims to learn the reverse of noise generation procedure • Network: Use the image-to-image translation (e.g., U-Net) architectures • Recall that input is 𝐱# and output is 𝐱#$%, both are images • It is expensive since both input and output are high-dimensional • Note that the denoiser 𝜇& 𝐱(, t shares weights, but conditioned by step 𝑡 Diffusion Probabilistic Model 16 * Image from the pix2pix-HD paper Sohl-Dickstein et al. Deep Unsupervised Learning using Nonequilibrium Thermodynamics. ICML’15
- 17. • Diffusion modelaims to learn the reverse of noise generation procedure • Sampling: Draw a random noise 𝒙" then apply the reverse step 𝑝&(𝐱#'%|𝐱#) • It often requires the hundreds of reverse steps (very slow) • Early and late steps change the high- and low-level attributes, respectively Diffusion Probabilistic Model 17 * Image from the DDPM paper Sohl-Dickstein et al. Deep Unsupervised Learning using Nonequilibrium Thermodynamics. ICML’15
- 18. • DDPM reparametrizesthe reverse distributions of diffusion models • Key idea: The original reverse step fully creates the denoiser 𝜇& 𝐱(, t from 𝐱# • However, 𝐱#$% and 𝐱# share most information, and thus it is redundant → Instead, create the residual 𝜖& 𝐱(, t and add to the original 𝐱# Denoising Diffusion Probabilistic Model (DDPM) 18 Ho et al. Denoising Diffusion Probabilistic Models. NeurIPS'20
- 19. • DDPM reparametrizesthe reverse distributions of diffusion models • Key idea: The original reverse step fully creates the denoiser 𝜇& 𝐱(, t from 𝐱# • However, 𝐱#$% and 𝐱# share most information, and thus it is redundant → Instead, create the residual 𝜖& 𝐱(, t and add to the original 𝐱# • Formally, DDPM reparametrizes the learned reverse distribution as1 and the step-wise objective 𝐿#$% can be reformulated as2 Denoising Diffusion Probabilistic Model (DDPM) 19 1. 𝛼! are some constants determined by 𝛽! 2. Note that we need no “intermediate” samples, and only compare the forward noise 𝝐 and reverse noise 𝝐" conditioned on 𝐱# Ho et al. Denoising Diffusion Probabilistic Models. NeurIPS'20
- 20. • DDPM initiatedthe diffusion model boom • Achieved SOTA on CIFAR-10, with high-resolution scalability • It produces more diverse samples than GAN (no mode collapse) Denoising Diffusion Probabilistic Model (DDPM) 20 Ho et al. Denoising Diffusion Probabilistic Models. NeurIPS'20
- 21. • DDIM roughlysketches the final sample, then refine it with the reverse process • Motivation: • Diffusion model is slow due to the iterative procedure • GAN/VAE creates the sample by one-shot forward operation • ⇒ Can we combine the advantages for fast sampling of diffusion models? • Technical spoiler: • Instead of naïvely applying diffusion model upon GAN/VAE, DDIM proposes a principled approach of rough sketch + refinement Denoising Diffusion Implicit Model (DDIM) 21 Song et al. Denoising Diffusion Implicit Models. ICLR’21
- 22. • DDIM roughlysketches the final sample, then refine it with the reverse process • Key idea: • Given 𝐱#, generate the rough sketch 𝐱! and refine 𝑝&(𝐱#$%|𝐱#, 𝐱!)1 • Unlike original diffusion model, it is not a Markovian structure Denoising Diffusion Implicit Model (DDIM) 22 1. Recall that the original diffusion model uses 𝑝"(𝐱$%&|𝐱$) Song et al. Denoising Diffusion Implicit Models. ICLR’21
- 23. • DDIM roughlysketches the final sample, then refine it with the reverse process • Key idea: Given 𝐱#, generate the rough sketch 𝐱! and refine 𝑞(𝐱#$%|𝐱#, 𝐱!) • Formulation: Define the forward distribution 𝑞(𝐱#$%|𝐱#, 𝐱!) as then, the forward process is derived from Bayes’ rule Denoising Diffusion Implicit Model (DDIM) 23 Song et al. Denoising Diffusion Implicit Models. ICLR’21
- 24. • DDIM roughlysketches the final sample, then refine it with the reverse process • Key idea: Given 𝐱#, generate the rough sketch 𝐱! and refine 𝑞(𝐱#$%|𝐱#, 𝐱!) • Formulation: Forward process is and reverse process is Denoising Diffusion Implicit Model (DDIM) 24 Song et al. Denoising Diffusion Implicit Models. ICLR’21
- 25. • DDIM roughlysketches the final sample, then refine it with the reverse process • Key idea: Given 𝐱#, generate the rough sketch 𝐱! and refine 𝑞(𝐱#$%|𝐱#, 𝐱!) • Formulation: Forward process is and reverse process is • Training: The variational lower bound of DDIM is identical to the one of DDPM1 • It is surprising since the forward/reverse formulation is totally different Denoising Diffusion Implicit Model (DDIM) 25 1. Precisely, the bound is different, but the solution is identical under some assumption (though violated in practice) Song et al. Denoising Diffusion Implicit Models. ICLR’21
- 26. • DDIM significantlyreduces the sampling steps of diffusion model • Creates the outline of the sample after only 10 steps (DDPM needs hundreds) Denoising Diffusion Implicit Model (DDIM) 26 Song et al. Denoising Diffusion Implicit Models. ICLR’21
- 27. • New goldenera of generative models • Competition of various approaches: GAN, VAE, flow, diffusion model1 • Also, lots of hybrid approaches (e.g., score SDE = diffusion + continuous flow) • Which model to use? • Diffusion model seems to be a nice option for high-quality generation • However, GAN is (currently) still a more practical solution which needs fast sampling (e.g., real-time apps.) Take-home Message 27 1. VAE also shows promising generation performance (see NVAE, very deep VAE)
- 28. 28 Thank you forlistening! 😀