![𝐼 𝑛 =
𝑑 𝑡
𝑡2 + 𝑎2 2
=
1
2𝑎2 𝑛 − 1
𝑡
𝑡2 + 𝑎2 𝑛−1
+
1
𝑎2
2𝑛 − 3
2𝑛 − 2
𝐼 𝑛−1
𝑠𝑒𝑐2
𝑢𝑑 𝑢 = 𝑡𝑔𝑢 + 𝑐
𝑐𝑠𝑐2
𝑢𝑑 𝑢 = −𝑐𝑡𝑔𝑢 + 𝑐
𝑠𝑒𝑐 𝑢. 𝑡𝑔𝑢. 𝑑 𝑢 = 𝑠𝑒𝑐𝑢 + 𝑐
𝑐𝑠𝑐 𝑢. 𝑐𝑡𝑔𝑢. 𝑑 𝑢 = −𝑐𝑠𝑐𝑢 + 𝑐
𝑐𝑡𝑔 𝑢. 𝑑 𝑢 = ln[𝑠𝑒𝑛𝑢] + 𝑐
𝑐𝑠𝑐 𝑢. 𝑑 𝑢 = ln[𝑐𝑠𝑐𝑢 − 𝑐𝑡𝑔𝑢] + 𝑐
𝑡𝑔 𝑢. 𝑑 𝑢 = ln[𝑠𝑒𝑐𝑢] + 𝑐
𝑠𝑒𝑐 𝑢. 𝑑 𝑢 = ln[𝑠𝑒𝑐𝑢 + 𝑡𝑔𝑢] + 𝑐
𝑑 𝑢
𝑎2 − 𝑢2
= arcsen
𝑢
𝑎
+ 𝑐
𝑑 𝑢
𝑢2 ± 𝑎2
= ln[u + 𝑢2 ± 𝑎2] + 𝑐
𝑑 𝑢
𝑢2 + 𝑎2
=
1
𝑎
𝑎𝑟𝑐𝑡𝑔
𝑢
𝑎
+ 𝑐
𝑑 𝑢
𝑢 𝑢2 − 𝑎2
=
1
𝑎
𝑎𝑟𝑠𝑒𝑐
𝑢
𝑎
+ 𝑐
𝑑 𝑢
𝑎2 − 𝑢2
=
1
2𝑎
ln[
𝑎 + 𝑢
𝑎 − 𝑢
] + 𝑐
𝑑 𝑢
𝑢2 − 𝑎2
=
1
2𝑎
ln[
𝑢 − 𝑎
𝑢 + 𝑎
] + 𝑐
𝒅 𝒖
𝒖 𝒂 𝟐 ± 𝒖 𝟐
=
−𝟏
𝒂
𝐥𝐧[
𝒂 + 𝒂 𝟐 ± 𝒖 𝟐
𝒖
] + 𝒄
𝒂 𝟐 − 𝒖 𝟐 𝒅 𝒖 =
𝒖
𝟐
𝒂 𝟐 − 𝒖 𝟐 +
𝒂 𝟐
𝟐
𝒂𝒓𝒄𝒐𝒔𝒆𝒏
𝒖
𝒂
+ 𝒄
𝒖 𝟐 + 𝒂 𝟐 𝒅 𝒖 =
𝒖
𝟐
𝒖 𝟐 + 𝒂 𝟐 +
𝒂 𝟐
𝟐
𝒍𝒏[𝒖 + 𝒖 𝟐 + 𝒂 𝟐] + 𝒄
𝒖 𝟐 − 𝒂 𝟐 𝒅 𝒖 =
𝒖
𝟐
𝒖 𝟐 − 𝒂 𝟐 −
𝒂 𝟐
𝟐
𝒍𝒏[𝒖 + 𝒖 𝟐 − 𝒂 𝟐] + 𝒄
𝒅 𝒖
𝒖 𝟐 ± 𝝀
= 𝐥𝐧[𝒖 + 𝒖 𝟐 ± 𝝀] + 𝒄
𝑎 𝑢
𝑑 𝑢 =
𝑎 𝑢
𝑙𝑛𝑎
+ 𝑐
𝑠𝑒𝑐𝑢 𝑑 𝑢 = −𝑐𝑜𝑠𝑢 + 𝑐
Algunas propiedades de derivadas
𝑥 𝑚 ′
= 𝑚𝑥 𝑚−1 1
𝑥
′
=
−1
𝑥2
𝑥
′
=
1
2 𝑥
𝑎 𝑥 ′
= 𝑎 𝑥
𝑙𝑛𝑎
𝑙𝑜𝑔 𝑎 𝑥 ′
=
1
𝑥𝑙𝑛𝑎
𝑐𝑜𝑠𝑥 ′
= −𝑠𝑒𝑛𝑥
𝑎𝑟𝑐𝑠𝑒𝑛𝑥 ′
=
1
1 − 𝑥2
𝑎𝑟𝑐𝑐𝑜𝑠𝑥 ′
=
−1
1 − 𝑥2
𝑎𝑟𝑐𝑡𝑔𝑥 ′
=
1
1 + 𝑥2
𝑎𝑟𝑐𝑐𝑡𝑔𝑥 ′
=
−1
1 + 𝑥2
𝑎𝑟𝑐𝑠𝑒𝑐𝑥 ′
=
1
[𝑥] 𝑥2 − 1
𝑎𝑟𝑐𝑐𝑠𝑐𝑥′
=
−1
[𝑥]𝑥2−1
Tabla de integrales definidas
JhonasAbnerVegaV.](https://image.slidesharecdn.com/integral-130427213140-phpapp01/85/tabla-de-Integral-2-320.jpg)
Uploaded byJhonás A. Vega
tabla de Integral
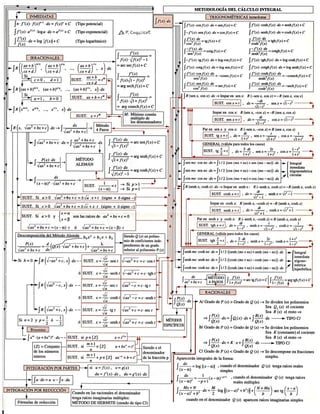
This document contains: 1) Formulas for derivatives of trigonometric, inverse trigonometric, logarithmic, and other functions. 2) Properties of derivatives such as the power rule and derivatives of composite functions. 3) A table of definite integrals.
More Related Content
![Manual funcionamiento CPHS [ACHS, 2000]](https://cdn.slidesharecdn.com/ss_thumbnails/comitc3a9-paritario-de-higiene-y-seguridad-151226002450-thumbnail.jpg?width=640&height=640&fit=bounds)
tabla de Integral
- 1. 𝒃 𝟎 𝒙𝟐 + 𝒃 𝟏 𝒙 + 𝒃 𝟐
- 2. 𝐼 𝑛 = 𝑑𝑡 𝑡2 + 𝑎2 2 = 1 2𝑎2 𝑛 − 1 𝑡 𝑡2 + 𝑎2 𝑛−1 + 1 𝑎2 2𝑛 − 3 2𝑛 − 2 𝐼 𝑛−1 𝑠𝑒𝑐2 𝑢𝑑 𝑢 = 𝑡𝑔𝑢 + 𝑐 𝑐𝑠𝑐2 𝑢𝑑 𝑢 = −𝑐𝑡𝑔𝑢 + 𝑐 𝑠𝑒𝑐 𝑢. 𝑡𝑔𝑢. 𝑑 𝑢 = 𝑠𝑒𝑐𝑢 + 𝑐 𝑐𝑠𝑐 𝑢. 𝑐𝑡𝑔𝑢. 𝑑 𝑢 = −𝑐𝑠𝑐𝑢 + 𝑐 𝑐𝑡𝑔 𝑢. 𝑑 𝑢 = ln[𝑠𝑒𝑛𝑢] + 𝑐 𝑐𝑠𝑐 𝑢. 𝑑 𝑢 = ln[𝑐𝑠𝑐𝑢 − 𝑐𝑡𝑔𝑢] + 𝑐 𝑡𝑔 𝑢. 𝑑 𝑢 = ln[𝑠𝑒𝑐𝑢] + 𝑐 𝑠𝑒𝑐 𝑢. 𝑑 𝑢 = ln[𝑠𝑒𝑐𝑢 + 𝑡𝑔𝑢] + 𝑐 𝑑 𝑢 𝑎2 − 𝑢2 = arcsen 𝑢 𝑎 + 𝑐 𝑑 𝑢 𝑢2 ± 𝑎2 = ln[u + 𝑢2 ± 𝑎2] + 𝑐 𝑑 𝑢 𝑢2 + 𝑎2 = 1 𝑎 𝑎𝑟𝑐𝑡𝑔 𝑢 𝑎 + 𝑐 𝑑 𝑢 𝑢 𝑢2 − 𝑎2 = 1 𝑎 𝑎𝑟𝑠𝑒𝑐 𝑢 𝑎 + 𝑐 𝑑 𝑢 𝑎2 − 𝑢2 = 1 2𝑎 ln[ 𝑎 + 𝑢 𝑎 − 𝑢 ] + 𝑐 𝑑 𝑢 𝑢2 − 𝑎2 = 1 2𝑎 ln[ 𝑢 − 𝑎 𝑢 + 𝑎 ] + 𝑐 𝒅 𝒖 𝒖 𝒂 𝟐 ± 𝒖 𝟐 = −𝟏 𝒂 𝐥𝐧[ 𝒂 + 𝒂 𝟐 ± 𝒖 𝟐 𝒖 ] + 𝒄 𝒂 𝟐 − 𝒖 𝟐 𝒅 𝒖 = 𝒖 𝟐 𝒂 𝟐 − 𝒖 𝟐 + 𝒂 𝟐 𝟐 𝒂𝒓𝒄𝒐𝒔𝒆𝒏 𝒖 𝒂 + 𝒄 𝒖 𝟐 + 𝒂 𝟐 𝒅 𝒖 = 𝒖 𝟐 𝒖 𝟐 + 𝒂 𝟐 + 𝒂 𝟐 𝟐 𝒍𝒏[𝒖 + 𝒖 𝟐 + 𝒂 𝟐] + 𝒄 𝒖 𝟐 − 𝒂 𝟐 𝒅 𝒖 = 𝒖 𝟐 𝒖 𝟐 − 𝒂 𝟐 − 𝒂 𝟐 𝟐 𝒍𝒏[𝒖 + 𝒖 𝟐 − 𝒂 𝟐] + 𝒄 𝒅 𝒖 𝒖 𝟐 ± 𝝀 = 𝐥𝐧[𝒖 + 𝒖 𝟐 ± 𝝀] + 𝒄 𝑎 𝑢 𝑑 𝑢 = 𝑎 𝑢 𝑙𝑛𝑎 + 𝑐 𝑠𝑒𝑐𝑢 𝑑 𝑢 = −𝑐𝑜𝑠𝑢 + 𝑐 Algunas propiedades de derivadas 𝑥 𝑚 ′ = 𝑚𝑥 𝑚−1 1 𝑥 ′ = −1 𝑥2 𝑥 ′ = 1 2 𝑥 𝑎 𝑥 ′ = 𝑎 𝑥 𝑙𝑛𝑎 𝑙𝑜𝑔 𝑎 𝑥 ′ = 1 𝑥𝑙𝑛𝑎 𝑐𝑜𝑠𝑥 ′ = −𝑠𝑒𝑛𝑥 𝑎𝑟𝑐𝑠𝑒𝑛𝑥 ′ = 1 1 − 𝑥2 𝑎𝑟𝑐𝑐𝑜𝑠𝑥 ′ = −1 1 − 𝑥2 𝑎𝑟𝑐𝑡𝑔𝑥 ′ = 1 1 + 𝑥2 𝑎𝑟𝑐𝑐𝑡𝑔𝑥 ′ = −1 1 + 𝑥2 𝑎𝑟𝑐𝑠𝑒𝑐𝑥 ′ = 1 [𝑥] 𝑥2 − 1 𝑎𝑟𝑐𝑐𝑠𝑐𝑥′ = −1 [𝑥]𝑥2−1 Tabla de integrales definidas JhonasAbnerVegaV.