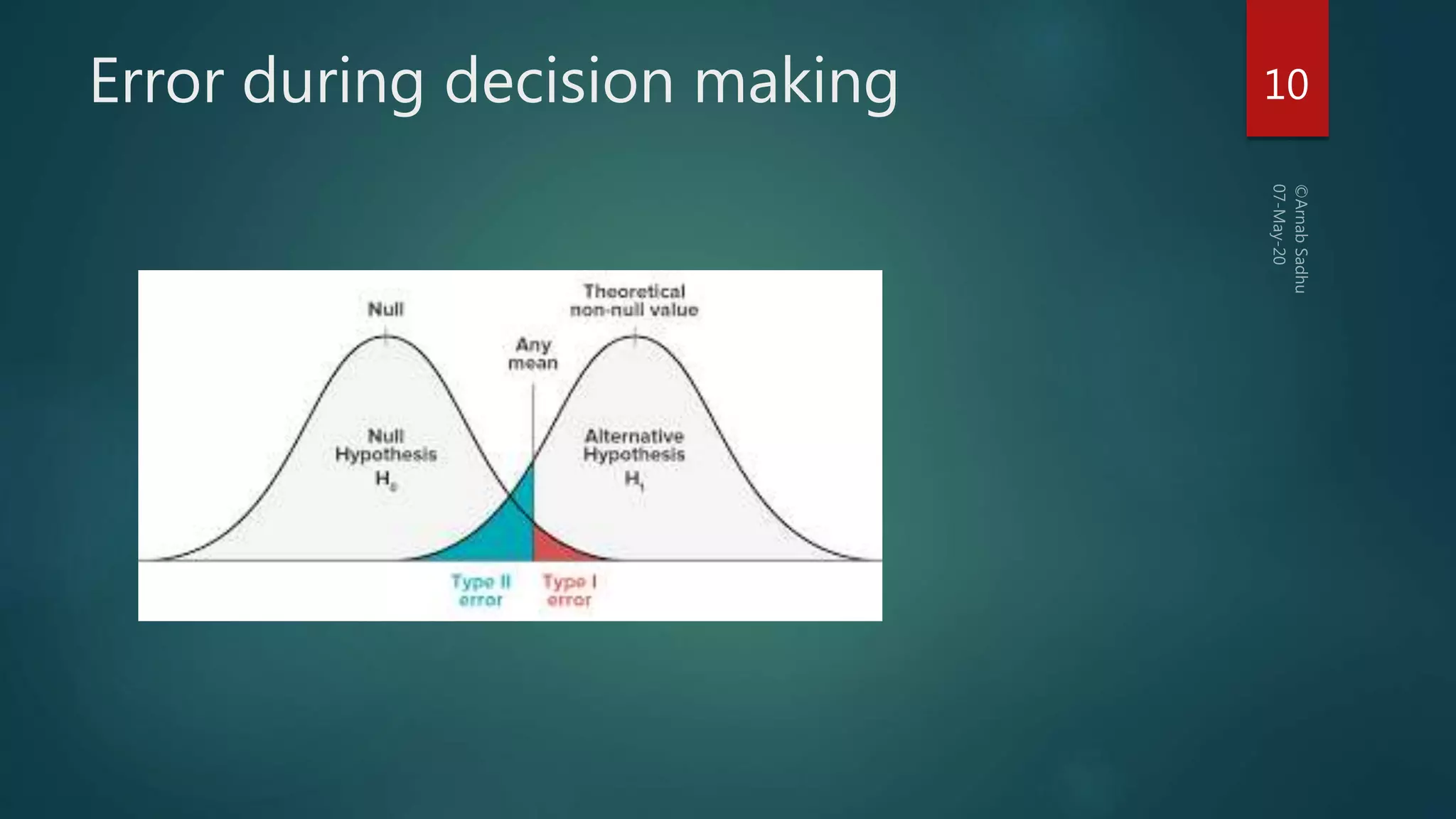
This document discusses hypotheses testing, which is a statistical technique used to test hypotheses about populations based on sample data. It defines key terms like the null hypothesis (H0), which is the hypothesis being tested, and the alternative hypothesis (HA or H1), which contradicts the null hypothesis. Researchers aim to reject the null hypothesis to establish something novel. The document outlines the steps of hypothesis testing, including formulating the hypotheses, identifying relevant test statistics, setting a significance level, doing computations, and making a decision to either accept or reject the null hypothesis. It discusses types of tests like z-tests and t-tests and the concept of critical values. The document also explains the two types of errors that can occur in decision making

1. Hypotheses Testing
ARNAB SADHU
SISTER NIVEDITA UNIVERSITY

2. What is Hypothesis
 It is a statistical technique to test some hypothesis about the
population from which the sample is drawn.
 It is an idea that can be tested on ground of statistical data.
 Eg. :
 Iphone are costly
• this is infeasible as it is not testable
Iphone are costly, given that we consider any price greater than Rs.40k as costly
• this is feasible as it is testable
2

3. Formulation of Hypotheses
Hypotheses
Null Hypothesis
𝐻0
It is the hypothesis that is to be tested
Alternate Hypothesis
𝐻𝐴 𝑜𝑟 𝐻1
It is the hypothesis that in some sense
contradicts the null hypothesis
3
 Researchers always try to reject the null hypothesis to establish something novel
 Null hypothesis is accepted to be true until proven wrong, it is like innocent until
proven guilty

4. Example
 Statement: Mean blood sugar level in India is 80 mg/dL
4
The mean
is
80mg/dL
The mean
is not
80mg/dL
NullHypothesis(𝑯𝟎)
AlternateHypothesis
(𝑯𝑨)

5. Procedure of hypothesis testing
 Step 1: Set up the hypotheses: 𝐻0 𝑎𝑛𝑑 𝐻𝐴
 Step 2: Identify the test statistics and its probability
distribution
 Step 3: Set up a suitable significant level (𝛼).
 Test of validity of 𝐻0 against 𝐻𝐴at certain level of
significance
 Eg. 5%, 1% etc.
 5% level of significance means, we are taking wrong
decision 5% time.
5

6. Types of testing 6

7. Critical 𝑧-value
 𝑧-value: It is a standardized score that describes how many standard
deviations (𝜎) an element is from the given mean (𝜇).
Table of critical 𝑧-value
7
Confidence level = 100-significance level
Level of 10% 5% 1% 0.1%
Two tailed 1.65 1.96 2.58 3.29
One tailed 1.28 1.64 2.33 3.10

8. Procedure of hypothesis testing
 Step 3: Setting a test criteria
 Selection of appropriate probability distribution for the test.
 Eg. t-test, F-test etc.
 We most often use, z score as,
 Step 4: Doing computation
 Step 5: Making decision
 Either accept 𝐻0 or reject it
𝒛 =
𝒙 − 𝝁
𝝈 𝒏
8

9. Error during decision making 9
𝐻0 is true
𝐻0 is accepted
𝐻𝐴 is true
𝐻0 is accepted
𝐻0 is true
𝐻0 is rejected
𝐻𝐴 is true
𝐻0 is rejected
Truth
𝑯 𝟎 𝑯 𝑨
Decision
Accept 𝑯 𝟎
Reject 𝑯 𝑨
type II error
type I
error

10. Error during decision making 10

11. Problem Example
 A random sample of 50 items give the mean 6.2, and variance 10.24. Can it
be regarded as drawn from normal population with mean 5.4 at 5%
significance?
11