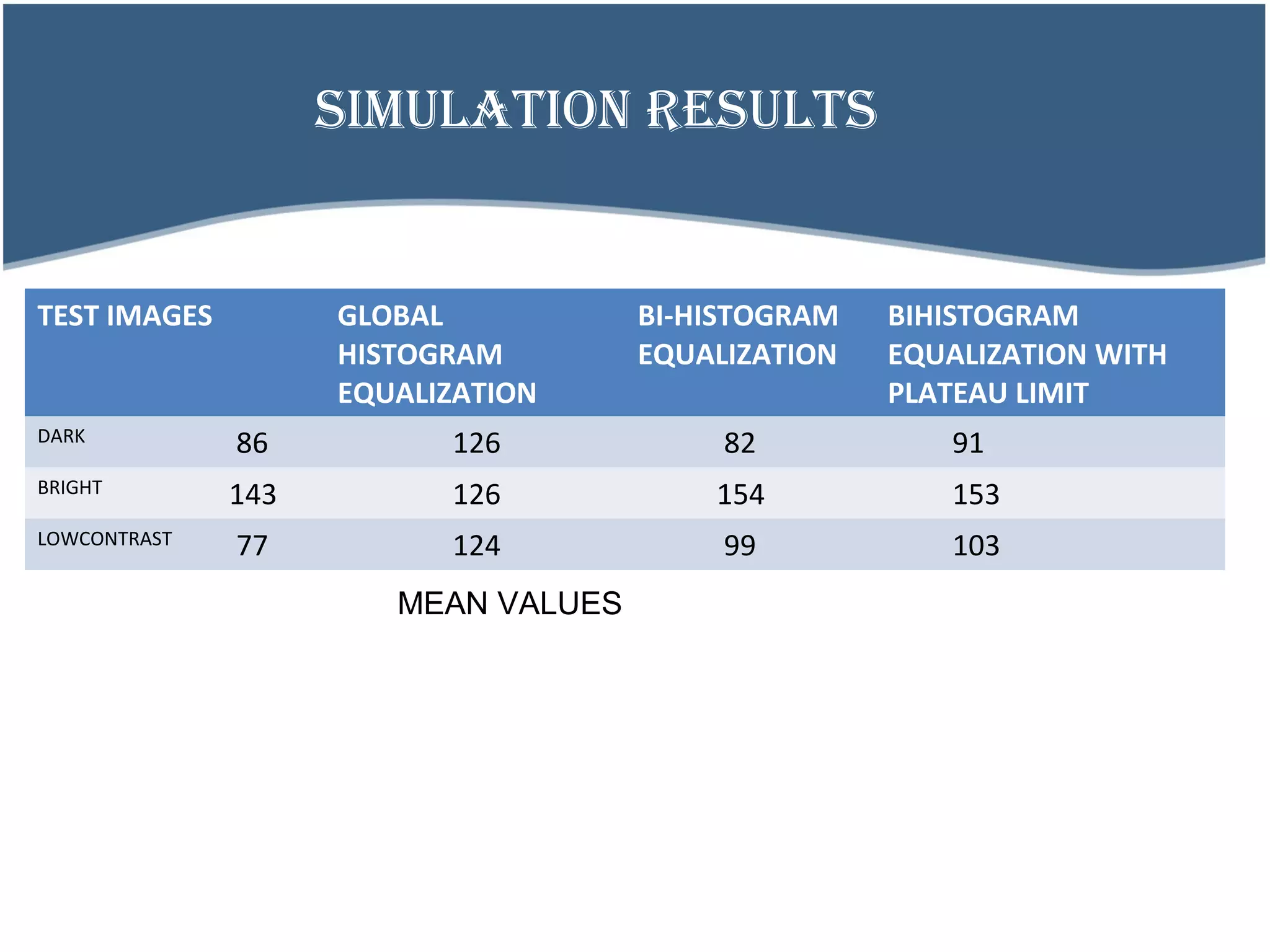
The document presents a comprehensive overview of bi-histogram equalization with a plateau limit for digital images, highlighting the concept and techniques of histogram equalization and its various methods. It discusses the properties of digital images, histograms, and the different equalization methods along with their drawbacks, and explains how bi-histogram equalization addresses these issues by conserving the mean intensity values. The document concludes with simulation results comparing the effectiveness of different equalization methods in enhancing image contrast.

1. BI-HISTOGRAM EQUALIZATION
wITH A pLATEAU LIMIT
FOR DIGITAL IMAGES.
MAHESH MOHAN.M.R
GECT S1 ECE
ROLL NO: 7
GUIDE : Dr.V.S.SHEEBA
OM NAMA
SIVAYA

2. OBJECTIVE
.
TO FAMILARIZE WITH
.HISTOGRAM EQUALIZATION
.DIFFERENT EQUALIZATION METHODS
.THEIR DRAWBACK AND HOW IT IS RECTIFIED.

3. FLOw OF SEMINAR.
1.WHAT IS A DIGITAL IMAGE?
2.WHAT IS A HISTOGRAM?
3.WHAT IS HISTOGRAM EQUALIZATION?
4.DIFFERENT EQUALIZATION METHODS AND ITS DRAWBACK.
5.HOW DRAWBACK OF EACH METHOD IS RECTIFED?

4. • A digital image is a matrix representation of a
two-dimensional image.
wHAT IS A DIGITAL IMAGE?
Colour imageGray scale image(Black and white)

5. dGray Image
Image
wHAT IS A GRAy SCALE IMAGE?
243 121
.
34 21
.
. .
Gray level matrix
0 255

6. Image matrix
Image
wHAT IS A COLOUR IMAGE?
234 212 123
135 231 233
.
121 222
. .
243 121
.
. . .
112 167
.
. . .
Red matrix
Green matrix
Blue matrix
.
.

7. wHAT IS A HISTOGRAM?
Consider a 5x5 image with integer intensities in the range between zero and seven:
0 7 3 2 3
0 0 0 6 7
7 7 2 2 0
1 1 0 4 1
0 0 7 4 1
Image matrixImage
0 1 2 3 4 5 6 7
Gray scale
Black White

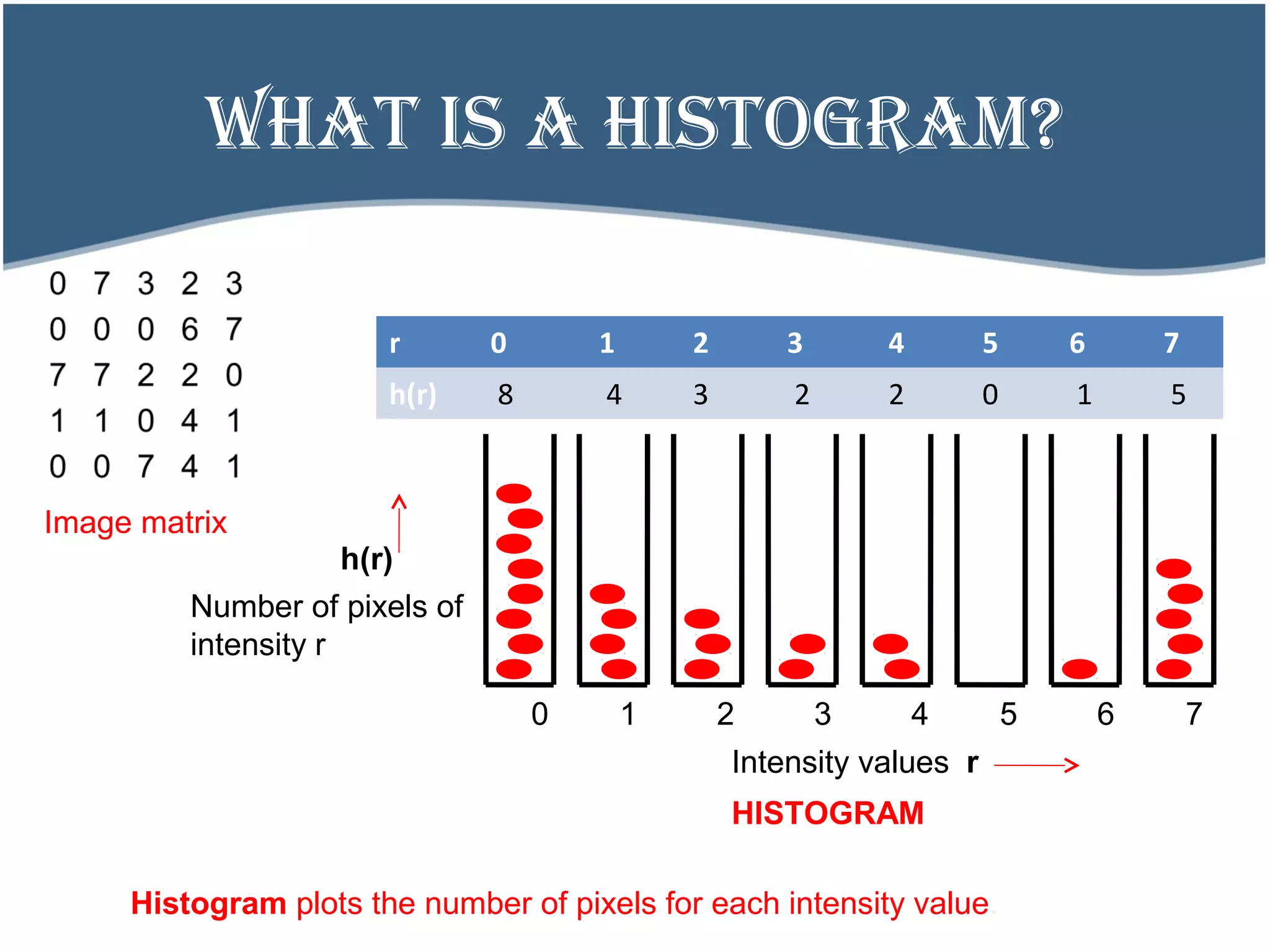
8. wHAT IS A HISTOGRAM?
Consider a 5x5 image with integer intensities in the range between one and eight:
0 7 3 2 3
0 0 0 6 7
7 7 2 2 0
1 1 0 4 1
0 0 7 4 1
Image matrixImage
0 1 2 3 4 5 6 7
Grey scale
Black White
Number of pixel with intensity value 0 [h(r0)] = 8

9. wHAT IS A HISTOGRAM?
0 7 3 2 3
0 0 0 6 7
7 7 2 2 0
1 1 0 4 1
0 0 7 4 1
Image matrixImage
0 1 2 3 4 5 6 7
Grey scale
Black White
Number of pixel with intensity value 0 [h(r0)] = 8
Similarly for 1 h(r1) = 4

10. wHAT IS A HISTOGRAM?
0 7 3 2 3
0 0 0 6 7
7 7 2 2 0
1 1 0 4 1
0 0 7 4 1
Image matrixImage
Similarly
INTENSITY r 0 1 2 3 4 5 6 7
NUMBER of
pixels of r
h(r)
h(r0)=8 h(r1)=4 h(r2)=3 h(r3)=2 h(r4)=2 h(r5)=0 h(r6)=1 h(r7)=5

11. r
wHAT IS A HISTOGRAM?
Image matrix
0 1 2 3 4 5 6 7
HISTOGRAM
Intensity values
Number of pixels of
intensity r
r 0 1 2 3 4 5 6 7
h(r) 8 4 3 2 2 0 1 5
Histogram plots the number of pixels for each intensity value.
h(r)

12. What is a histogram?
r 0 1 2 3 4 5 6 7
h(r) 8 4 3 2 2 0 1 5
p(r)
h(r)/(5*5)
8/25 4/25 3/25 2/25 2/25 0/25 1/25 5/25
HISTOGRAM - h(r) - Y axis - number of intensities
NORMALIZED HISTOGRAM - p(r) - Y axis - probability of intensities

13. SAMPLE IMAGES AND ITS HISTOGRAM
Bright image
Intensity range 0 - 255

14. SAMPLE IMAGES AND ITS HISTOGRAM
Bright image
Intensity range 0 - 255
0 50 100 150 200 255
Intensity
No:ofpixels
DARK BRIGHT
h(r)

15. SAMPLE IMAGES AND ITS HISTOGRAM
Dark image
Intensity range 0 - 255

16. SAMPLE IMAGES AND ITS HISTOGRAM
Dark image
Intensity range 0 - 255
0 50 100 150 200 255
Intensity
No:ofpixels
h(r)

17. SAMPLE IMAGES AND ITS HISTOGRAM
Low contrast image
Intensity range 0 - 255

18. SAMPLE IMAGES AND ITS HISTOGRAM
Light image
Intensity range 0 - 255
0 50 100 150 200 255
Intensity
No:ofpixels
h(r)

19. SAMPLE IMAGES AND ITS HISTOGRAM
Bright image
Dark image
Low contrast
image

20. SAMPLE IMAGES AND ITS HISTOGRAM
High contrast image
Intensity range 0 - 255
0 50 100 150 200 255
Intensity
No:ofpixels
h(r)

21. CoNCEPt oF histogram EQUaLiZatioN
ORIGINAL IMAGE EQUALIZED IMAGE
MAXIMIZES ENTROPY OF AN IMAGE.
s1 s2

22. thEorY BEhiND histogram
EQUaLiZatioN
TRANSFORMATION FUNCTION THAT MAPS THE
INPUT INTENSITY TO ALL AVAILABLE INTENSITIES.
I/p intensity
O/p intensity

23. THEORY BEHIND HISTOGRAM
EQUALIZATION
ORIGINAL IMAGE EQUALIZED IMAGE
s1 s2

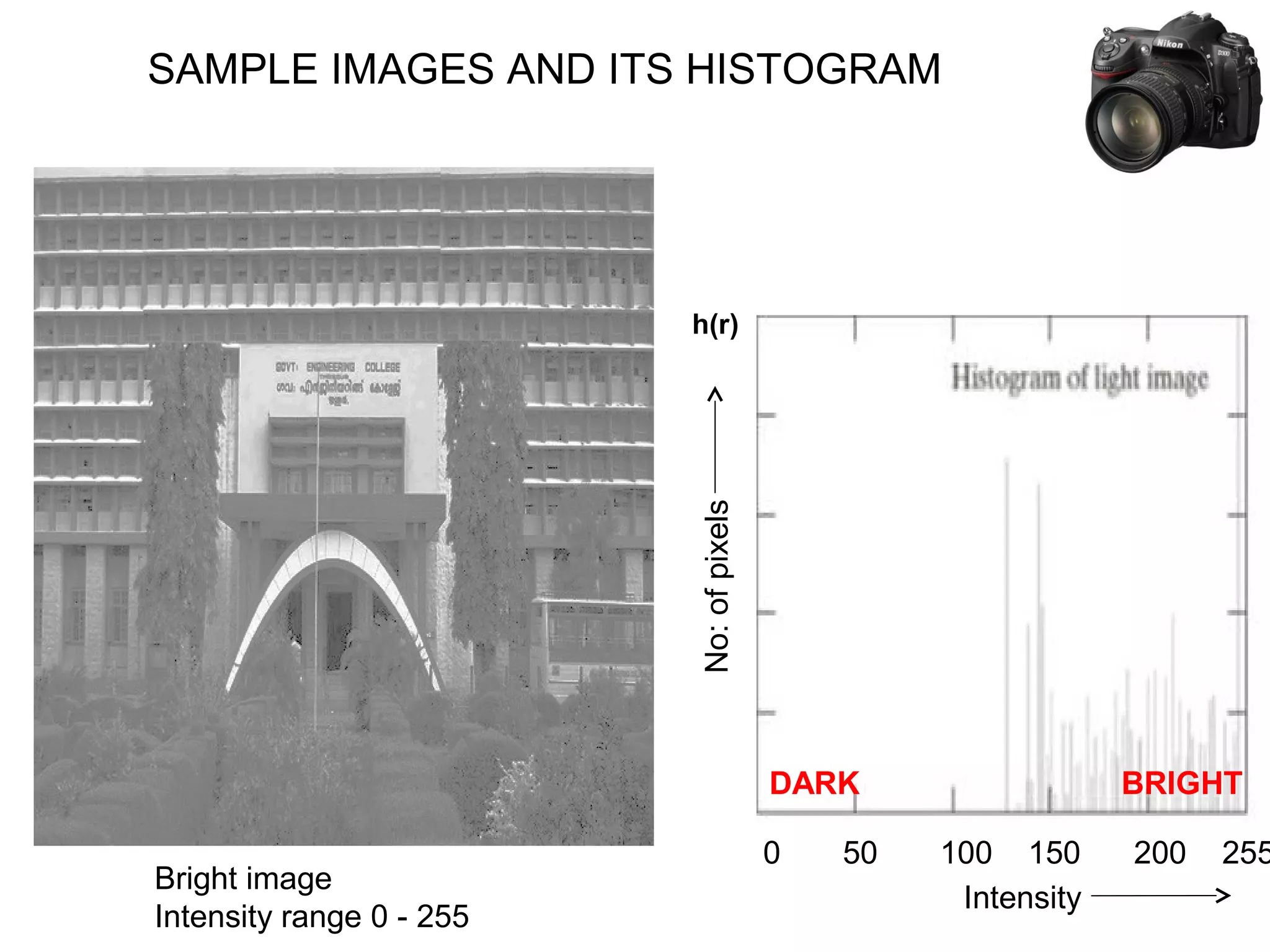
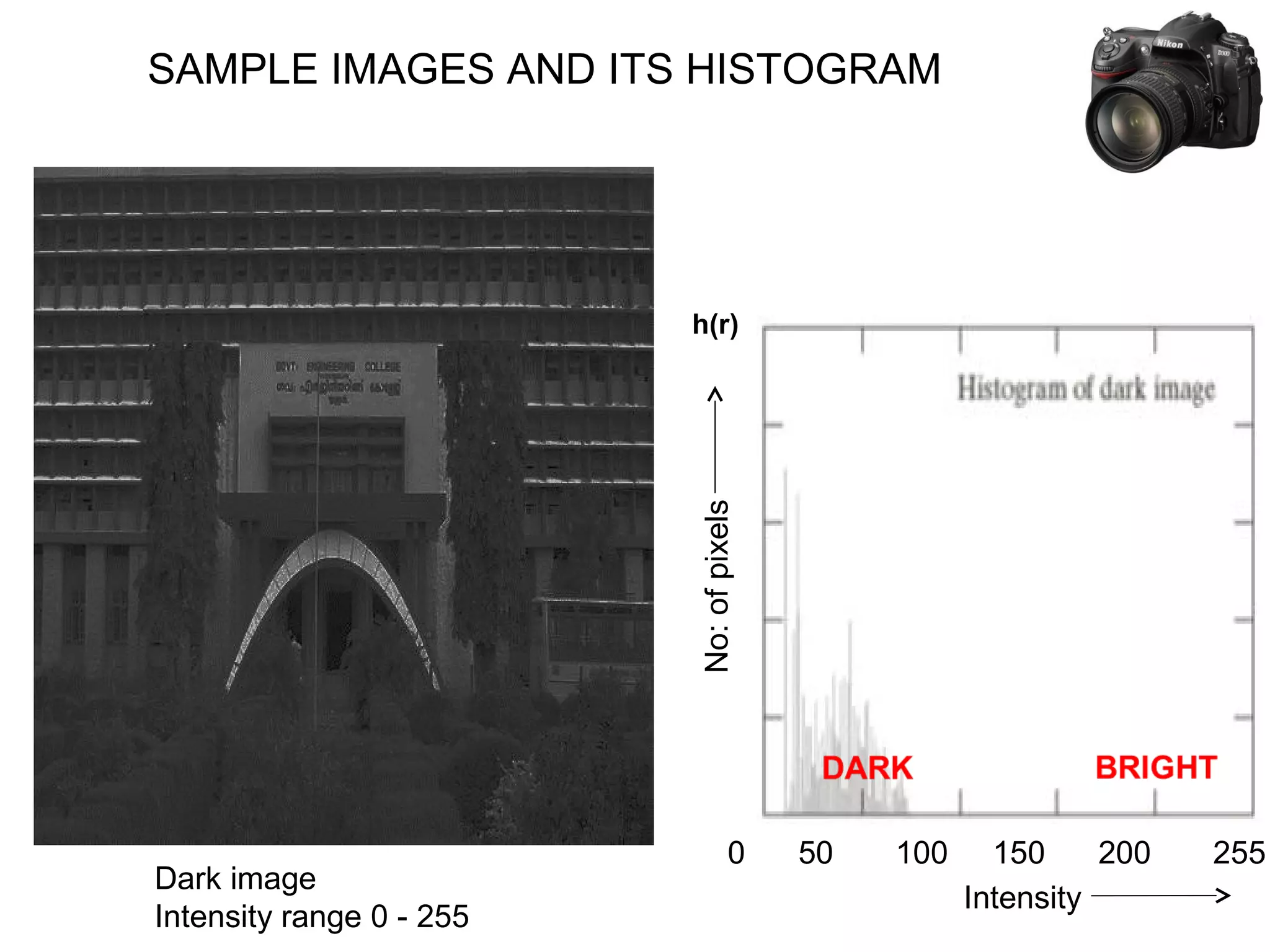
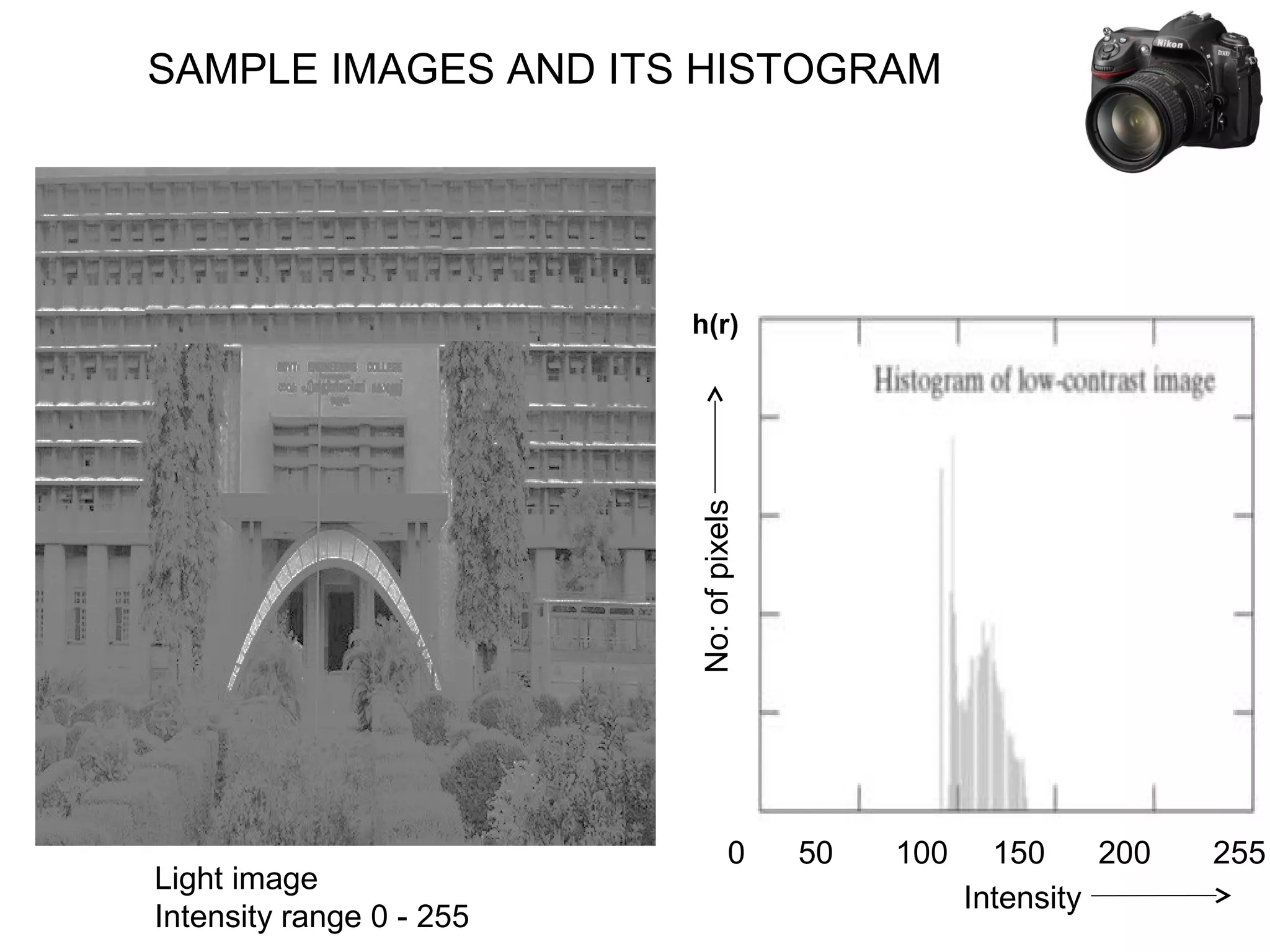
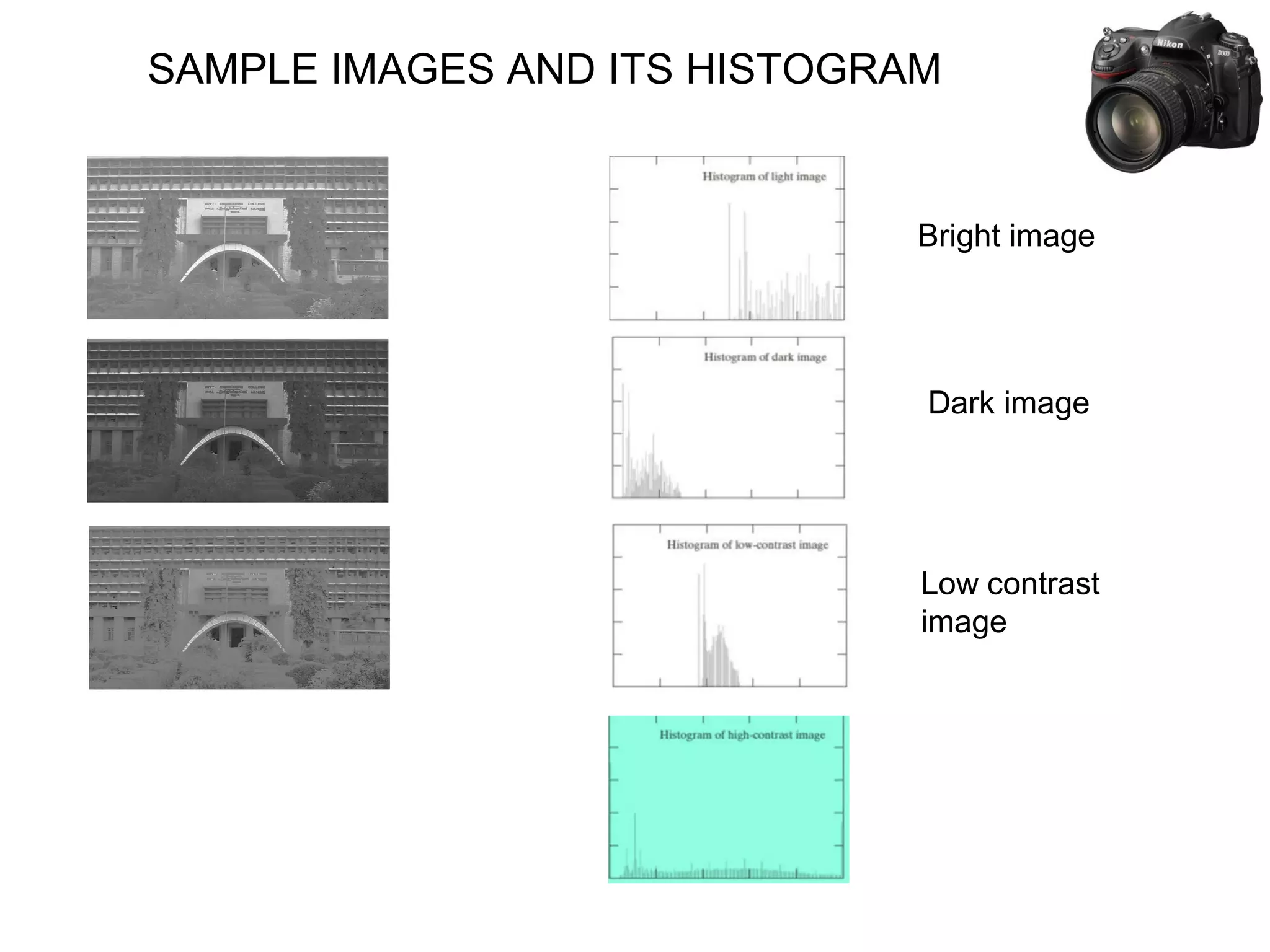
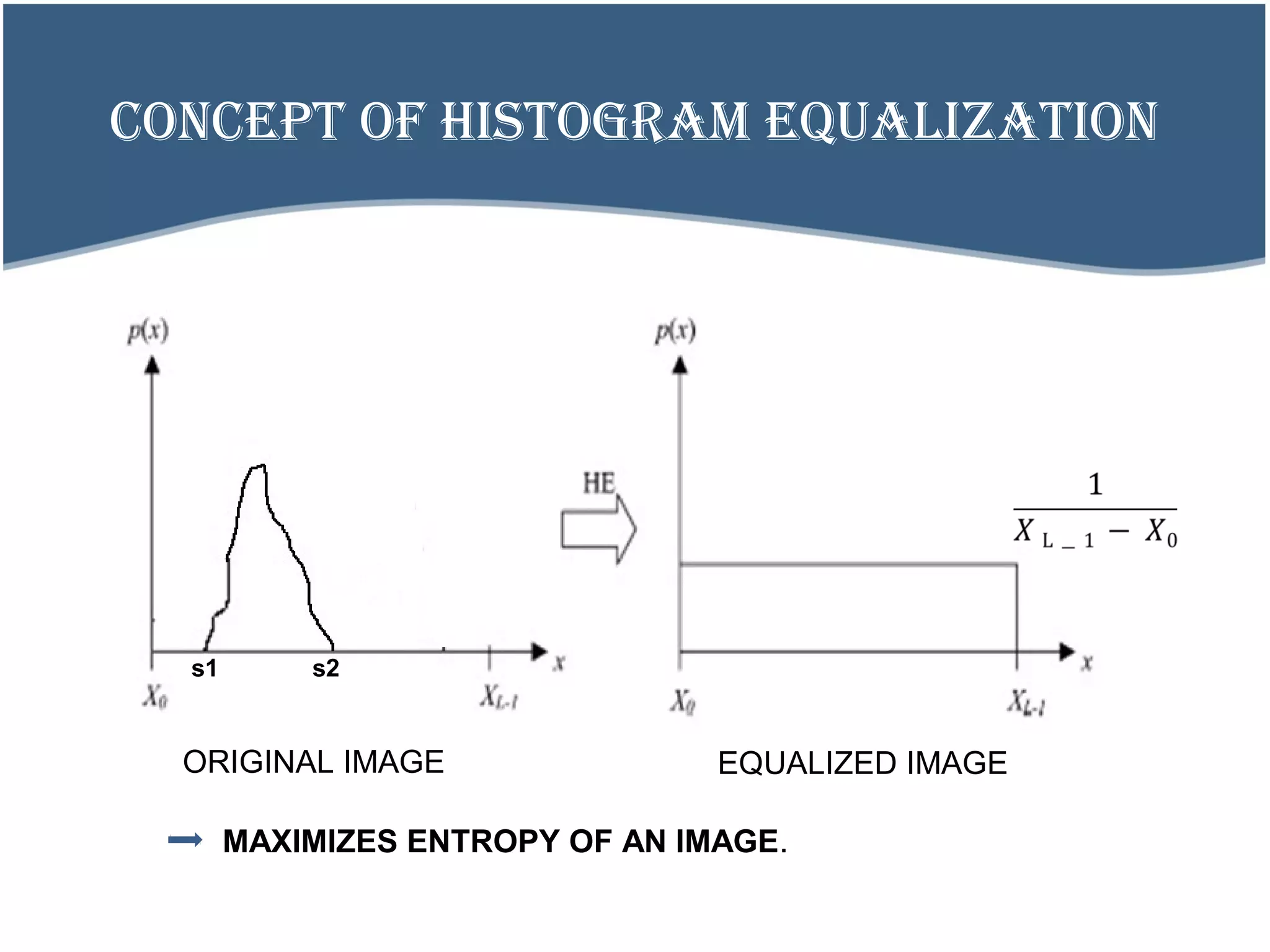
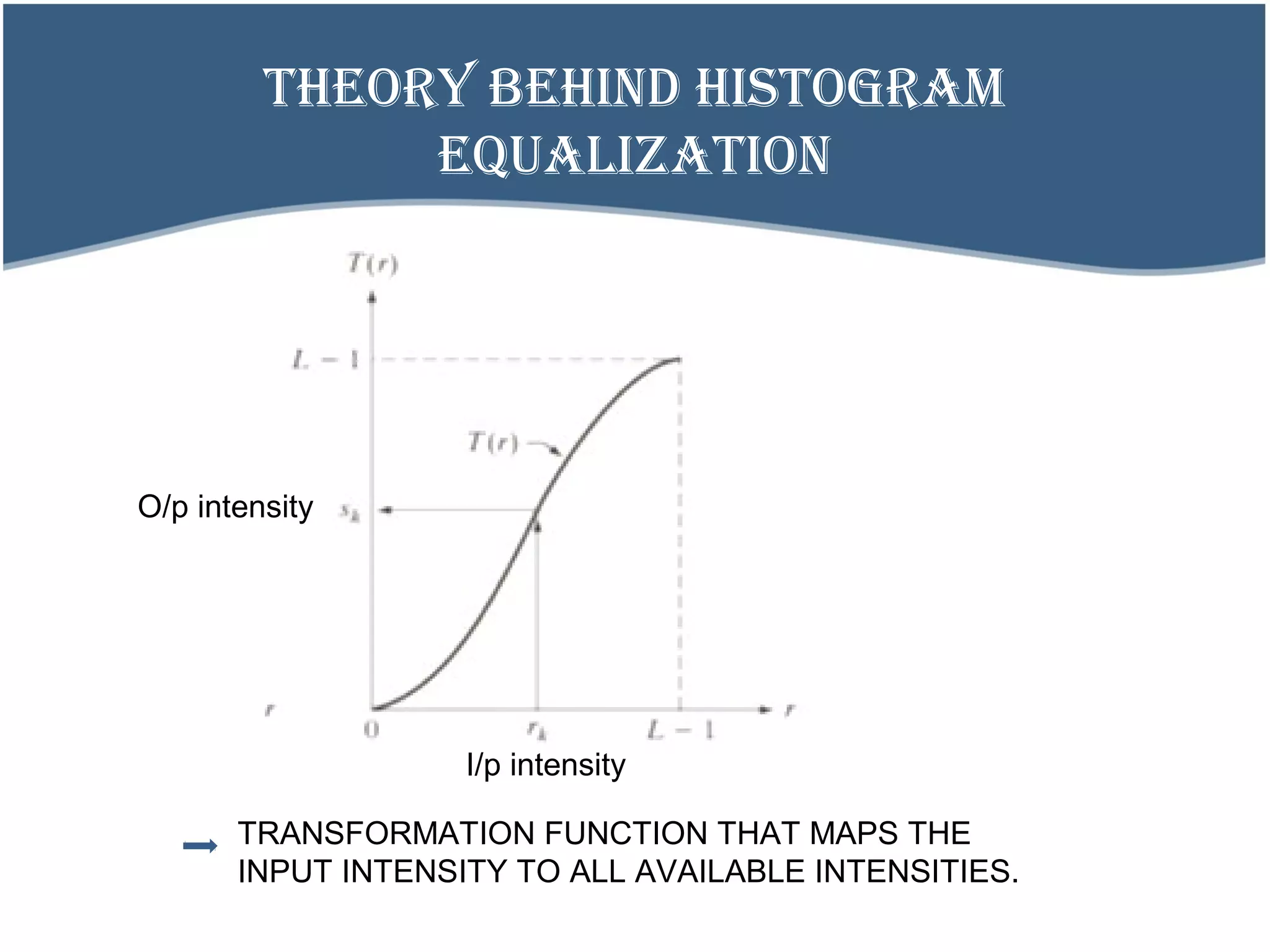
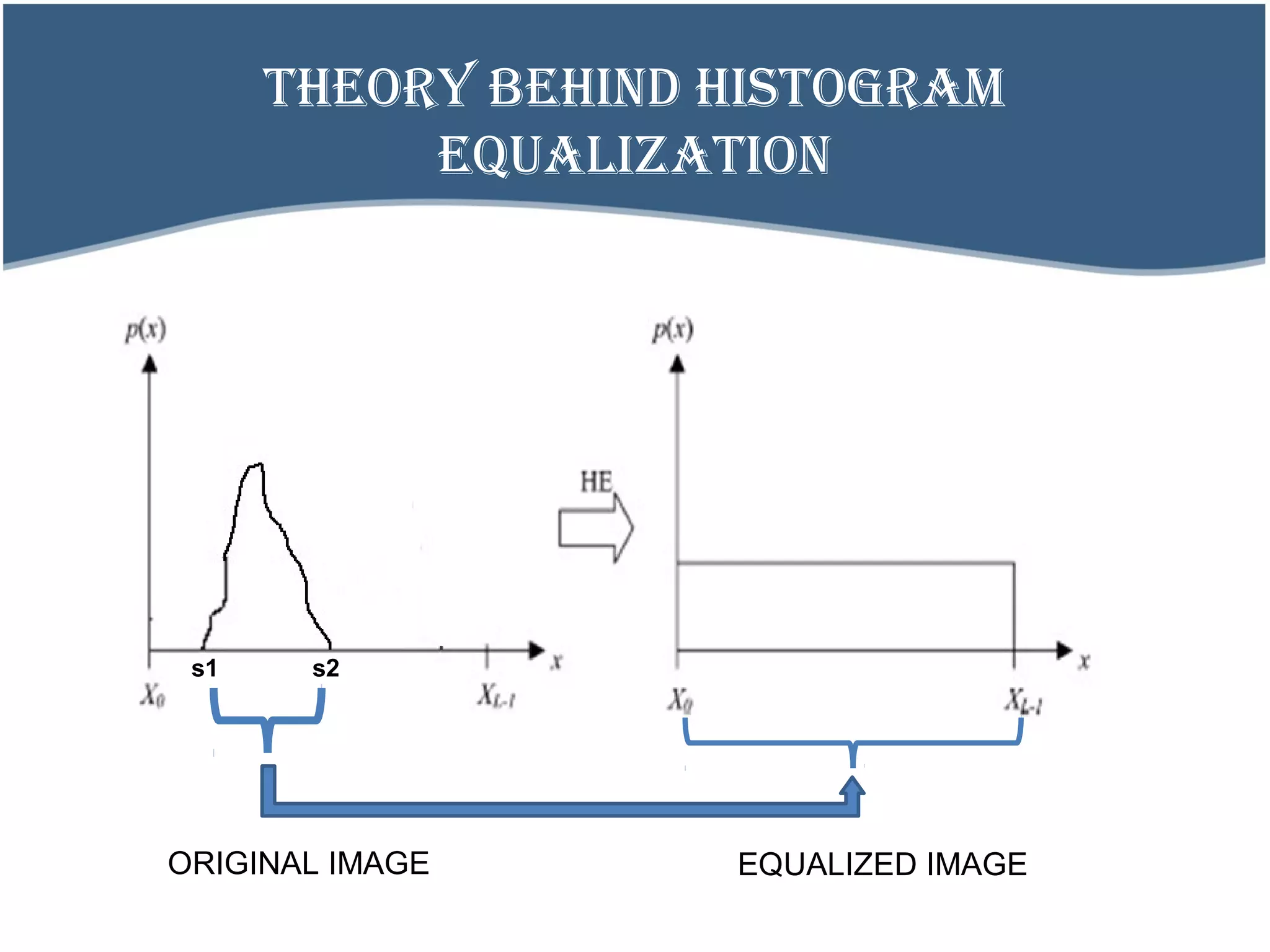
24. THEORY BEHIND HISTOGRAM
EQUALIZATION
CUMULATIVE DISTRIBUTION
FUNCTION T(r)
0 50 100 150 200 255
[76 – 213]
[0 – 48]
[15 – 100] [25 – 125]
O/P INTENSITY = X0 + [( Xl-1 –X0 )*C(x)]
I/P intensity

25. DIFFERENT STAGES
GLOBAL HISTOGRAM
EQUALIZATION
BI-HISTOGRAM
EQUALIZATION
BI-HISTOGRAM
EQUALIZATION
WITH A PLATEAU LIMIT

26. GLOBAL HISTOGRAM EQUALIZATION
OBTAIN
HISTOGRAM
OBTAIN PDF
OBTAIN CDF
OBTAIN
TRANSFORMATIO
N FUNCTION
MAPPING OF NEW
INTENSITY VALUES
NEW HISTOGRAM
Original histogram
M*N
PDF
1..
CDF
1
x0
XL-1
O/P
x0
XL-1
MappingTransformation
function
t1
t2
t2
New histogram
t1t1 t2
t2t1t2t1

27. GLOBAL HISTOGRAM EQUALIZATION
RESULTS
GHE
O/P MEAN CONSTANTWHY ?

28. GLOBAL HISTOGRAM EQUALIZATION
DRAWBACK
DO NOT CONSERVE THE MEAN.
WHY MEAN IMPORTANT?
Video frames
GHE

29. THEORY OF BIHISTOGRAM EQUALIZATION
HISTOGRAM EQUALIZED SEPERATELY AROUND MEAN.
THUS CONSERVE THE MEAN.
ORIGINAL HISTOGRAM BIHISTOGRAM EQUALIZED

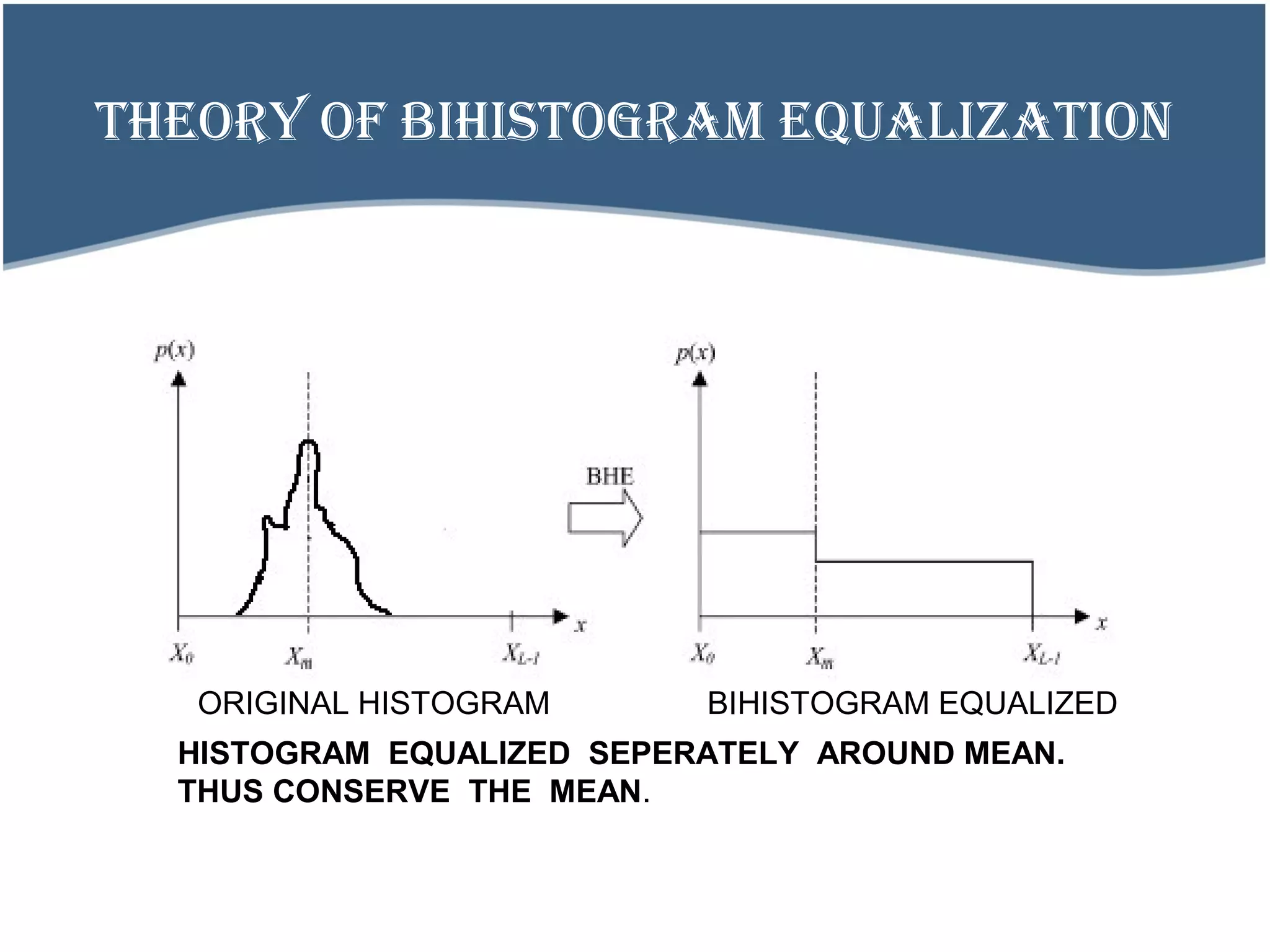
30. BIHISTOGRAM EQUALIZATION
OBTAIN PDF
(lower subimage)[X0-Xm]
OBTAIN CDF
OBTAIN
TRANSFORMATIO
N FUNCTION
MAPPING OF NEW
INTENSITY VALUES
NEW HISTOGRAM
DIVIDE HISTOGRAM WITH RESPECT TO
INTENSITY MEAN (X m ).
OBTAIN
HISTOGRAM
OBTAIN PDF
(upper subimage)[Xm-Xl-1]
OBTAIN CDF
OBTAIN
TRANSFORMATIO
N FUNCTION
MAPPING OF NEW
INTENSITY VALUES
+
GHE
GHE
Partition
Merging

31. BI-HISTOGRAM EQUALIZATION RESULTS
BHE

32. BIHISTOGRAM EQUALIZATION DRAWBACK
LEVEL SATURATION DUE TO HIGH PROBABLE
INTENSITY VALUES.
BHE
EXAMPLE
WHY IT HAPPENS ?

33. THOERY OF BIHISTOGRAM EQUALIZATION
WITH A PLATEAU LIMIT .
BIHISTOGRAM CLIPPING HISTOGRAM
ABOVE PLATEAU LIMIT
TL PLATEAU LIMITS FOR LOWER HISTOGRAM.
TU PLATEAU LIMITS FOR UPPER HISTOGRAM.
SELECT PLATEAU LIMIT

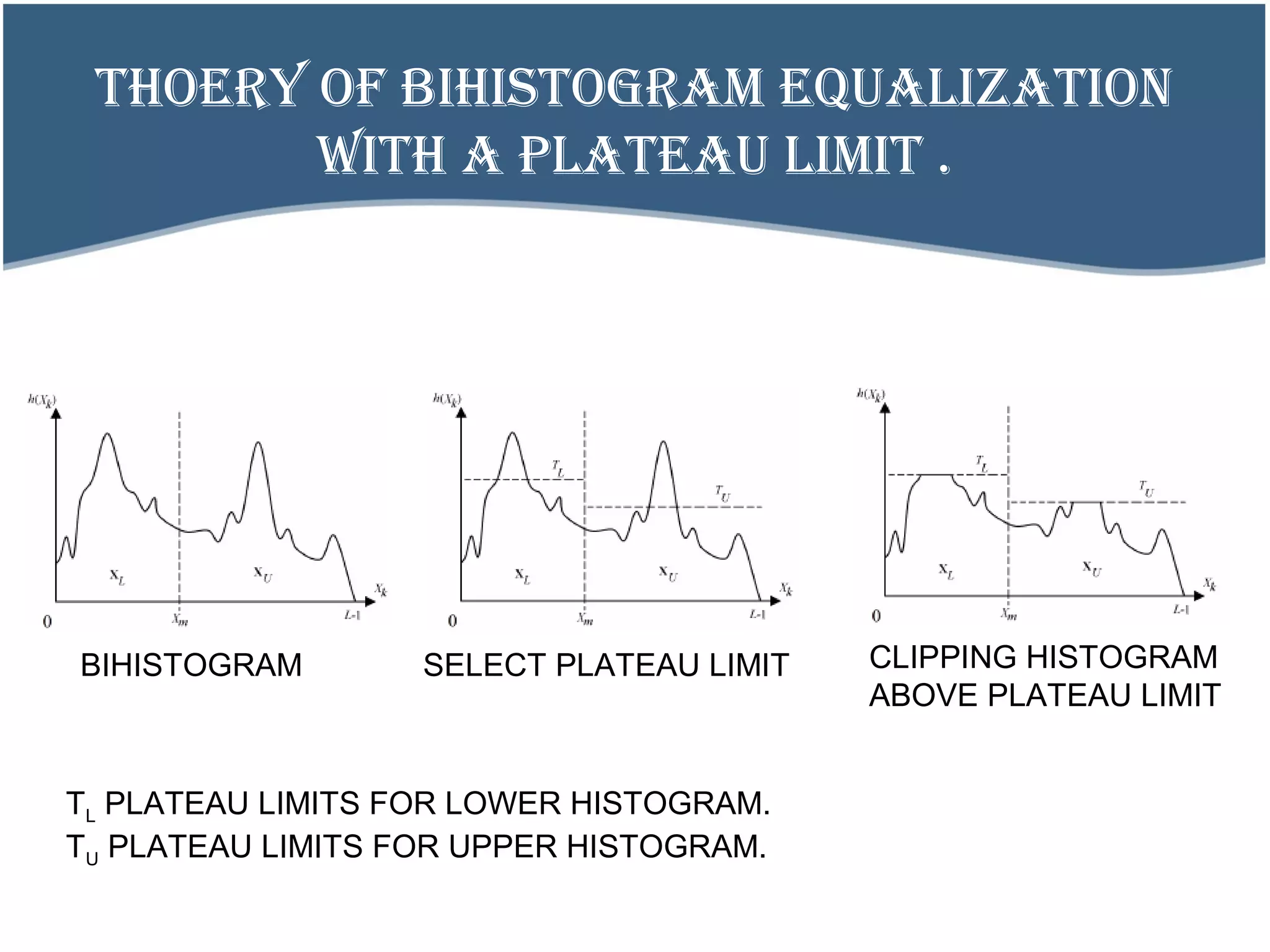
34. BIHISTOGRAM EQUALIZATION WITH A
PLATEAU LIMIT
OBTAIN PDF
(lower subimage)[X0-Xm]
OBTAIN CDF
OBTAIN
TRANSFORMATION
FUNCTION
MAPPING OF NEW
INTENSITY VALUES
NEW HISTOGRAM
DIVIDE HISTOGRAM WITH RESPECT TO
INTENSITY MEAN (X m ).
OBTAIN
HISTOGRAM
OBTAIN PDF
(upper subimage)[Xm-Xl-1]
OBTAIN CDF
OBTAIN
TRANSFORMATION
FUNCTION
MAPPING OF NEW
INTENSITY VALUES
+
GHE
GHE
Partition
Merging
CLIP WRT
AMPLITUDE MEAN
CLIP WRT
AMPLITUDE MEAN
Clipping

35. BIHISTOGRAM EQUALIZATION WITH A
PLATEAU LIMIT RESULTS
BHEPL

36. SIMULATION RESULTS
TEST IMAGES GLOBAL
HISTOGRAM
EQUALIZATION
BI-HISTOGRAM
EQUALIZATION
BIHISTOGRAM
EQUALIZATION WITH
PLATEAU LIMIT
DARK 86 126 82 91
BRIGHT 143 126 154 153
LOWCONTRAST 77 124 99 103
MEAN VALUES

37. SIMULATION RESULTS
LEVEL SATURATION
TEST IMAGES BI-HISTOGRAM
EQUALIZATION
BIHISTOGRAM
EQUALIZATION WITH
PLATEAU LIMIT
WHITE DOT YES NO

38. d
WHY GRAY SCALE IMAGES INSTEAD
OF COLOUR IMAGES?
.

39. CONCLUSIONHistogram?
IN AN IMAGE
NOTHING WORSE MORE THAN LOW CONTRAST
GLOBAL HISTOGRAM EQUALIZATION
NOTHING WORSE MORE THAN MEAN CONSERVATION
BI-HISTOGRAM EQUALIZATION
NOTHING WORSE MORE
THAN ………………?
NOTHING WORSE MORE THAN LEVEL SATURATION
BI-HISTOGRAM EQUALIZATION WITH PLATEAU LIMIT

40. REFERENCESStogram?
Bi-Histogram Equalization with a Plateau Limit
for Digital Image Enhancement
Chen Hee Ooi, Student Member, IEEE, Nicholas Sia Pik Kong,
Student Member, IEEEand Haidi Ibrahim, Member, IEEE
IEEE Transactions on Consumer Electronics, Vol. 55, No. 4,
NOVEMBER 2009
Contrast Enhancement Using Brightness Preserving
Bi-Histogram Equalization
YEONG-TAEG KIM, MEMBER, IEEE
Color Image Enhancement Using Brightness Preserving
Dynamic Histogram Equalization
Nicholas Sia Pik Kong, Student Member, IEEE, and Haidi
Ibrahim, Member, IEEE.
Preserving brightness in histogram equalization
based contrast enhancement techniques
Soong-Der Chen a, Abd. Rahman Ramli
Digital image processing by Gonzalez and Woods

41. NAMASIVAYA

42. • Lorem ipsum dolor sit amet, consectetuer
adipiscing elit. Vivamus et magna. Fusce sed
sem sed magna suscipit egestas.
• Lorem ipsum dolor sit amet, consectetuer
adipiscing elit. Vivamus et magna. Fusce sed
sem sed magna suscipit egestas.
1

43. • Lorem ipsum dolor sit amet, consectetuer
adipiscing elit. Vivamus et magna. Fusce sed
sem sed magna suscipit egestas.
• Lorem ipsum dolor sit amet, consectetuer
adipiscing elit. Vivamus et magna. Fusce sed
sem sed magna suscipit egestas.
1