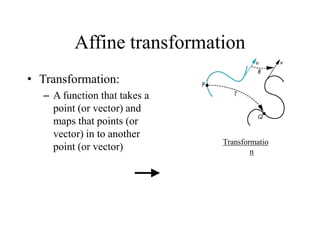
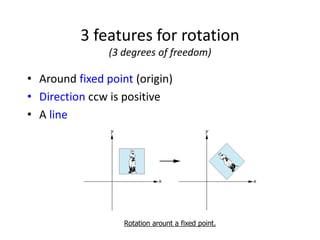
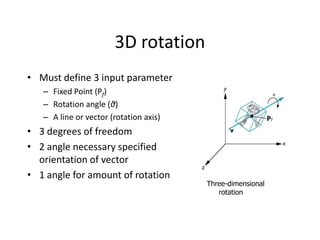
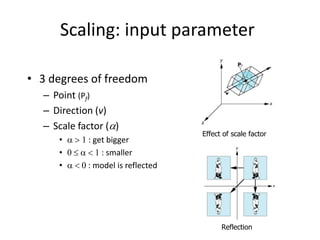
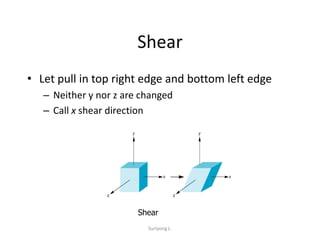
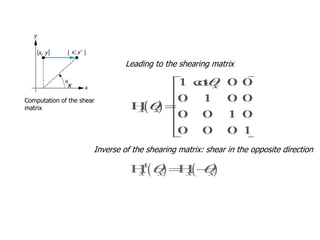
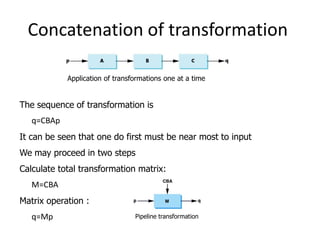
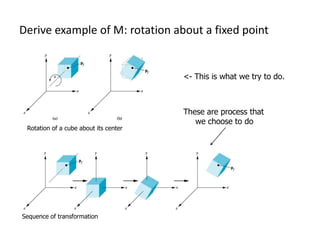
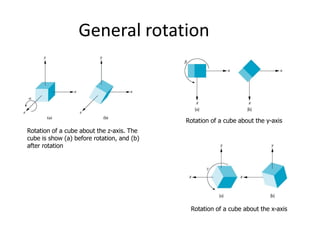
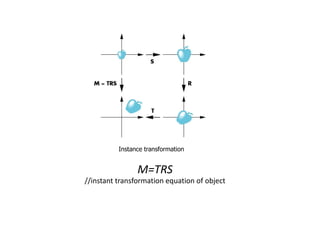
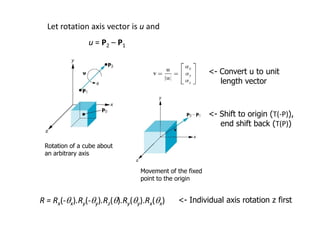
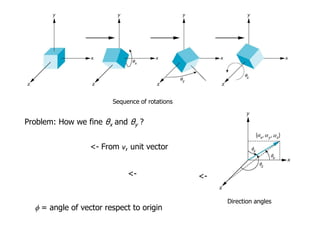
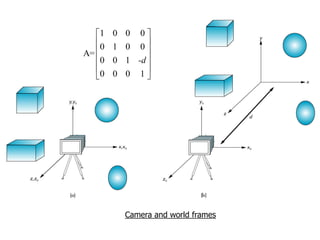
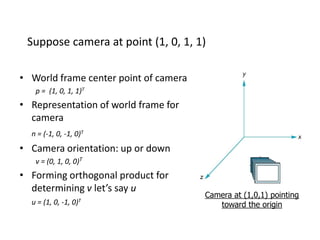
OpenGL uses model-view and projection matrices to apply transformations like translation, rotation, and scaling. The document discusses constructing transformation matrices for different types of transformations, including translation, rotation around fixed points and arbitrary axes, scaling, and shearing. It also covers combining multiple transformations using matrix multiplication and storing transformations in the current transformation matrix.

1. Geometric Objects and
Transformations -I
By: Saad Siddiqui

2. Frames in OpenGL
• 2 frames:
– Camera: regard as fix
– World:
• The model-view matrix position related to camera
• Convert homogeneous coordinates representation of object to camera
frame
• OpenGL provided matrix stack for store model view
matrices or frames
• By default camera and world have the same origin
• If moving world frame distance d from camera the
model-view matrix would be

3. 1
0
A= 
0

0
0
0

0 1 -d 

0 0 1
0 0
1 0
Camera and world frames

4. Suppose camera at point (1, 0, 1, 1)
• World frame center point of camera
p = (1, 0, 1, 1)T
• Representation of world frame for
camera
n = (-1, 0, -1, 0)T
• Camera orientation: up or down
v = (0, 1, 0, 0)T
• Forming orthogonal product for
determining v let’s say u
u = (1, 0, -1,
0)T
Camera at (1,0,1) pointing
toward the origin

5. The model view matrix M
Result:
Original origin is 1 unit in the n direction from the origin in the camera frame
which is the point (0, 0, 1, 1)
OpenGL model view matrix
OpenGL set a model-view matrix by send an array of 16 elements to
glLoadMatrix
We use this for transformation like rotation, translation and scales etc.

6. Modeling a colored cube.
• A number of distinct task that we must perform to generate
the image
–
–
–
–
–
–
Modeling
Converting to the camera frame
Clipping
Projecting
Removing hidden surfaces
Rasterizing
One frame of cube animation

7. Modeling a Cube
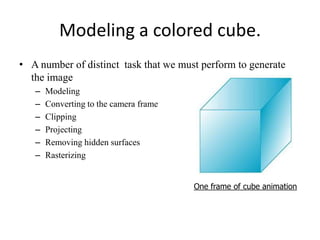
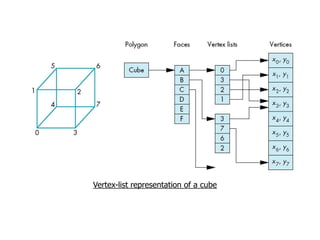
• Model as 6 planes intersection or six polygons as cube facets
• Ex. of cube definition
GLfloat vertices[8][3] = {
{-1.0,-1.0,-1.0}, {1.0,-1.0,-1.0},
{1.0,1.0,-1.0}, {-1.0,1.0,-1.0},
{-1.0,-1.0,1.0}, {1.0,-1.0,1.0},
{1.0,1.0,1.0}, {-1.0,1.0,1.0}
};
// or
typedef point3[3];
// then may define as
point3 vertices[8] = {
{-1.0,-1.0,-1.0}, {1.0,-1.0,-1.0},
{1.0,1.0,-1.0}, {-1.0,1.0,-1.0},
{-1.0,-1.0,1.0}, {1.0,-1.0,1.0},
{1.0,1.0,1.0}, {-1.0,1.0,1.0}
};
// object may defined as
void polygon(int a, int b, int c , int d) {
/* draw a polygon via list of vertices */
glBegin(GL_POLYGON);
glVertex3fv(vertices[a]);
glVertex3fv(vertices[b]);
glVertex3fv(vertices[c]);
glVertex3fv(vertices[d]);
glEnd();
}

8. Inward and outward pointing faces
• Be careful about the
order of vertices
• facing outward:
vertices order is 0, 3,
2, 1 etc., obey right
hand rule
Traversal of the edges of a
polygon

9. Data Structure for Object Representation
• Topology of Cube description
– Use glBegin(GL_POLYGON); six times
– Use glBegin(GL_QUADS); follow by 24 vertices
• Think as polyhedron
– Vertex shared by 3 surfaces
– Each pair of vertices define edges
– Each edge is shared by two faces

10. Vertex-list representation of a cube

11. The color cube
• Color to vertex list -> color 6 faces
• Define function “quad” for drawing quadrilateral polygon
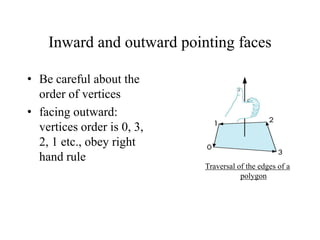
• Next define 6 faces, be careful about define outwarding
Glfloat vertices[8][3] = {{-1.0,-1.0, 1.0},{-1.0, 1.0, 1.0}, {1.0,1.0, 1.0}, {1.0,-1.0, 1.0},
{-1.0,-1.0,-1.0}, {1.0,-1.0,-1.0}, {1.0,1.0,-1.0}, {-1.0,1.0,-1.0}};
GLfloat colors[8][3] = {{0.0,0.0,0.0},{1.0,0.0,0.0}, {1.0,1.0,0.0}, {0.0,1.0,0.0},
{0.0,0.0,1.0}, {1.0,0.0,1.0}, {1.0,1.0,1.0}, {0.0,1.0,1.0}};
void quad(int a, int b, int c , int d) {
glBegin(GL_QUADS);
glColor3fv(colors[a]); glVertex3fv(vertices[a]); glColor3fv(colors[b]); glVertex3fv(vertices[b]);
glColor3fv(colors[c]); glVertex3fv(vertices[c]); glColor3fv(colors[d]); glVertex3fv(vertices[d]);
glEnd();
}
void colorcube() {
quad(0, 3, 2, 1); quad(2, 3, 7, 6); quad(0, 4, 7, 3); quad(1, 2, 6, 5); quad(4, 5, 6, 7); quad(0, 1, 5, 4);
}

12. Vertex Array
• Use encapsulation, data structure & method together
– Few function call
• 3 step using vertex array
– Enable functionality of vertex array: part of initialization
– Tell OpenGL where and in what format the array are: part of
initialization
– Render the object :part of display call back
• 6 different type of array
– Vertex, color, color index, normal texture coordinate and edge flag
– Enabling the arrays by
glEnableClientState(GL_COLOR_ARRAY);
glEnableClientState(GL_VERTEX_ARRAY);

13. // The arrays are the same as before and can be set up as globals:
GLfloat vertices[] = {{-1,-1,-1}, {1,-1,1}, {1,1,-1}, {-1,1,-1},{-1,-1,1}, {1,-1,1}, {1,1,1}, {-1,1,1}};
GLfloat colors[] = {{0,0,0}, {1,0,0},{1,1,0},{0,1,0},{0,0,1},{1,0,1}, {1,1,1},{0,1,1}};
// Next identify where the arrays are by
glVertexPointer(3, GL_FLOAT, 0, vertices);
glColorPointer(3, GL_FLOAT, 0, colors);
// Define the array to hold the 24 order of vertex indices for 6 faces
GLubyte cubeIndices[24] = {0,3,2,1, 2,3,7,6, 0,4,7,3, 1,2,6,5,
4,5,6,7,
0,1,5,4};
glDrawElements(type, n, format, pointer);
for (i=0; i<6; i++)
glDrawElement(GL_POLYGON, 4, GL_UNSIGNED_BYTE, &cubeIndex[4*i]};
// Do better by seeing each face as quadrilateral polygon
glDrawElements(GL_QUADS, 24, GL_UNSIGNED_BYTE, cubeIndices);
// GL_QUADS starts a new quadrilateral after each four vertices

14. Affine transformation
• Transformation:
– A function that takes a
point (or vector) and
maps that points (or
vector) in to another
point (or vector)
Transformatio
n
Q = f ( P),
v = f u  ,

15. Translation
Is an operation that displaces points by a fixed distance in a given direction
To specify a translation, just specify a displacement vector d thus
P = P  d
• For all point P of the object
– No reference point to frame or representation
– 3 degree of freedom
Translation. (a) Object in original position.
(b) Object translated

16. Rotation
• Need axis and angle as input parameter
x = r.cosf ;
Two-dimensional rotation
2D Point rotation θ radian around origin (Z axis)
x’ = r.cos(q  f
= r.cosf.cosq- r.sinf.sinq
= x.cosq – y.sinq
y’ = r.sin(qf)
= r.cosf.sinq +r.sinf.cosq
= x.sinq+y.cosq
These equations can be written in matrix form as
 x  cos q
 y =  sin q
  
y = r.sinf
- sin q   x 
cos q   y 
 

17. 3 features for rotation
(3 degrees of freedom)
• Around fixed point (origin)
• Direction ccw is positive
• A line
Rotation arount a fixed point.

18. 3D rotation
• Must define 3 input parameter
– Fixed Point (Pf)
– Rotation angle (θ)
– A line or vector (rotation axis)
• 3 degrees of freedom
• 2 angle necessary specified
orientation of vector
• 1 angle for amount of rotation
Three-dimensional
rotation

19. Scaling
• Non rigid-body transformation
• 2 type of scaling
– Uniform: scale in all direction -> bigger, smaller
– Nonuniform: scale in single direction
• Use in modeling and scaling
Non rigid body transformations
Uniform and nonuniform scaling

20. Scaling: input parameter
• 3 degrees of freedom
– Point (Pf)
– Direction (v)
– Scale factor ()
•  > 1 : get bigger
• 0   < 1 : smaller
•  < 0 : model is reflected
Effect of scale factor
Reflection

21. 3D primitives
Curves in three dimension
Surfaces in three
dimensions
Object are not lying on plane
Volumetric
objects

22. Homogeneous Coordinate
•
•
We use only 3 basis vector is not enough to make point and vector different
For any point:
P = P0  xv1  yv2  zv3
// General equation for point
In the frame specified by (v1, v2, v3, P0), any point P can be written uniquely as
P = 1v1   2v2  3v3  P0
The we can express this relation formally, using a matrix product, as
P = 1  2  3
 v1 
v 
1  2 
 v3 
 
 P0 
We may say that
 1 
 
P =  2
 3 
 
1
The yellow matrix called homogeneous-coordinate representation of point P

23. Transformation in homogeneous coordinate
Most graphics APIs force us to work within some reference system. Although we
can alter this reference system – usually a frame – we cannot work with high-level
representations, such as the expression.
Q = P + αv.
Instead, we work with representations in homogeneous coordinates, and with
expressions such as
q = p + αv.
Within a frame, each affine transformation is represented by a 4x4 matrix of the
form
é 11 12 13 14 ù

ê
ú
ê 21  22  23  24 ú

ê
ú
M= ê
 31  32  33  34 ú
ê
ú
ê0
0
0
1 ú
ë
û

24. Translation

25. Scaling
Use fixed point parameter as reference
Scaling in one direction means scale in each direction element

26. Rotation
2D rotation is actual 3D rotation around Z axis
For general equations:

28. Shear
• Let pull in top right edge and bottom left edge
– Neither y nor z are changed
– Call x shear direction
Shear
Suriyong L.

29. x = x  y cot q x
y = y
z = z
Leading to the shearing matrix
x
Computation of the shear
matrix
Inverse of the shearing matrix: shear in the opposite direction

30. Concatenation of transformation
Application of transformations one at a time
The sequence of transformation is
q=CBAp
It can be seen that one do first must be near most to input
We may proceed in two steps
Calculate total transformation matrix:
M=CBA
Matrix operation :
q=Mp
Pipeline transformation

31. Derive example of M: rotation about a fixed point
<- This is what we try to do.
Rotation of a cube about its center
Sequence of transformation
These are process that
we choose to do

33. General rotation
Rotation of a cube about the y-axis
Rotation of a cube about the z-axis. The
cube is show (a) before rotation, and (b)
after rotation
R = R xR yR z
Rotation of a cube about the x-axis

34. The Instance transformation
• From the example object, 2 options to do
with object
– Define object to its vertices and location
with the desire orientation and size
– Define each object type once at a
convenience size, place and orientation ,
next move to its place
• Object in the scene is instance of the
prototype
• If apply transformation, called instance
transformation
• We can use database and identifier for each
Scene of simple objects

35. Instance transformation
M=TRS
//instant transformation equation of object

36. Rotation around arbitrary axis
• Input parameter
– Object point
– Vector (line segment or 2 points)
– Angle of rotation
• Idea
– Translate to origin first T(-P0)
– Rotate
• q-axis component
• q around 1 component axis, let say z

37. Let rotation axis vector is u and
u = P2 – P1
<- Convert u to unit
length vector
<- Shift to origin (T(-P)),
end shift back (T(P))
Rotation of a cube about
an arbitrary axis
Movement of the fixed
point to the origin
R = Rx(-qx).Ry(-qy).Rz(q).Ry(qy).Rx(qx)
<- Individual axis rotation z first

38. Sequence of rotations
Problem: How we fine θx and θy ?
2
2
 x   y   z2 = 1
<- From v, unit vector
cos2 fx  cos2 fy  cos2 fz = 1 <-
cos fx =  x
cos f y =  y
<-
cos fz =  z
f = angle of vector respect to origin
Direction angles

39. OpenGL transformation matrices
• Use glMatrixMode function for selected
operation to apply
• Most graphic system use Current
Transformation Matrix (CTM) for any
transformation
Current transformation matrix (CTM)

40. CTM step
• Applied Identity matrix unless operate every round
– C <- I
• Applied Translation
– C <- CT
• Applied Scaling
– C <- CS
• Applied Rotation
– C <- CR
• Or postmultiply with M
– C <- M
or C <- CM

41. CTM: Translation, rotation and scaling
• CTM may be viewed as the part of all
primitive product GL_MODELVIEW and
GL_PROJECTION
• From function of glMatrixMode
Model-view and projection matrices

42. Rotation about a fixed point matrix step
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef(4.0, 5.0, 6.0);
glRotatef(45.0, 1.0, 2.0, 3.0);
glTranslatef(-4.0, -5.0, -6.0);
//rotate 45 deg. around a vector line 1,2,3
// with fixed point of (4, 5, 6)

43. c = a  ib = reiq
The quaternion
• Extension of complex number
• Useful for animation and hardware
implementation of rotation
• Consider the complex number
(a, b)
θ
• Like rotate point (a, b) around z axis with θ radian
• quaternion just like rotate in 3D space

44. Quaternion form
• q0 define rotation angle
• q define point

45. Multiplication properties
• Identity
– (1, 0)
• Inverse

46. Rotation with quaternion
• Let p=(0,p)
// point in space with p= (x,y,z)
• And unit quaternion r and its inverse r-1

47. Quaternion to Rotation Matrix
Replace: