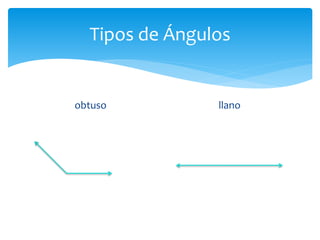
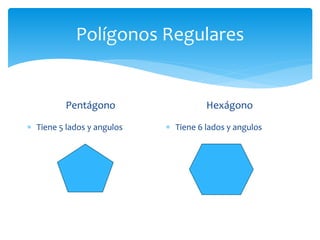
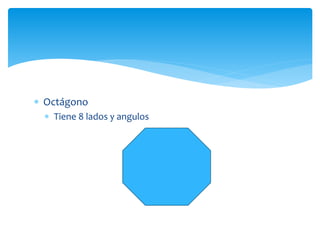
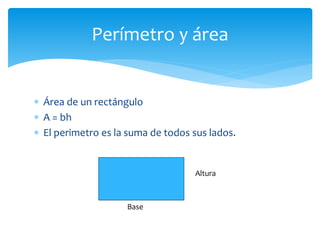
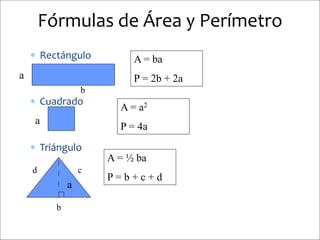
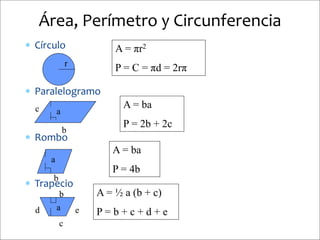
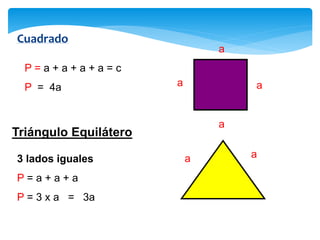
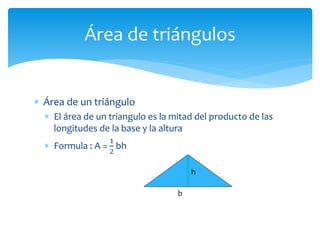
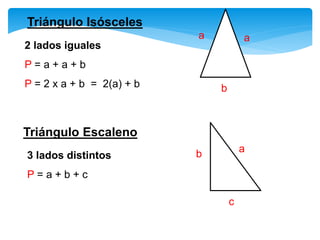
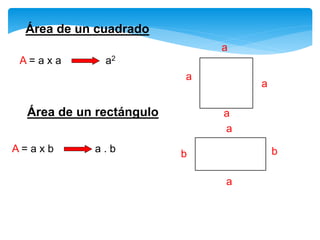
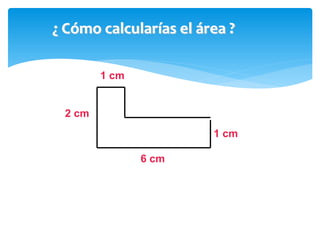
Este documento presenta información sobre figuras geométricas bidimensionales en el plano cartesiano. Introduce conceptos básicos como puntos, líneas y planos y define figuras como triángulos, cuadrados y círculos. Explica cómo calcular el área y perímetro de estas figuras usando fórmulas matemáticas. También incluye enlaces a recursos en línea y actividades prácticas para que los estudiantes apliquen los conceptos.

1. Universidad Interamericana de Puerto Rico
Recinto Metropolitano
Facultad de Ciencias y Tecnología
Propuesta LiNUS-MSP
Prof. Manuel Fernández

2. Título del Taller: Figuras bidimensionales en el
plano cartesiano.

3.  Estándar de Geometría:
 El estudiante es capaz de identificar formas
geométricas, analizar sus estructuras, características,
propiedades y relaciones para entender y descubrir el
entorno físico.
 Expectativas:
 Identifica, describe y clasifica las propiedades y las
relaciones entre las figuras bidimensionales y
tridimensionales.
Geometría

4. Introducción a la Geometría

5.  Si observamos nuestro entorno podemos ver
diferentes formas y figuras en los objetos que nos
rodean.
 Desde los primeros tiempos el ser humano se vio
obligado a observar, interpretar y manejar estas
figuras pues de ello dependía su sobrevivencia.
Elementos geométricos y el
concepto de los espacios

6.  Para tener más conocimientos debía clasificar
objetos, clasificar formas, establecer relaciones entre
las formas y los objetos e interpretar el significado de
cada uno de estos conceptos geométricos.
 Sabemos hoy día que el ser humano ha sido la especie
más exitosa sobre la faz de la tierra por que tiene un
atributo que lo hace único, su intelecto.

7.  Tenemos la capacidad de aprender y de aplicar nuestro
conocimiento para interpretar, manejar y transformar nuestro
medio ambiente.
 La geometría tiene sus orígenes en cada una de las antiguas
civilizaciones, egipcios, babilonios, romanos, griegos, etc., los cuales
fueron acumulando conocimiento de sus antepasados hasta hacer
de la Geometría una de las ramas más importantes en la
matemática.

8.  Al principio todo giraba alrededor de la geometría.
Las construcciones, la ingeniería rudimentaria, la
astronomía, e inclusive la alquimia que luego dio lugar
a la química, basaban su conocimiento en conceptos
geométricos.
 Fueron los griegos los que le dieron rigurosidad a la
geometría, estudiaron las figuras de forma y tamaño
idénticos (figuras congruentes) así como aquellas
figuras de forma idéntica pero con tamaños
diferentes (figuras similares).

9.  Los griegos fueron los primeros en insistir en que los
enunciados de la geometría debían tener una prueba
 rigurosa.

10.  La geometría plana se basa en tres conceptos
fundamentales, el punto, la línea y el plano, los que se
aceptan sin definirlos y que forman parte de lo que
llamamos espacios geométricos, o sea el conjunto
formado por todos los puntos.
 El espacio geométrico es relativo a los elementos que
se están usando. Por ejemplo, el espacio puede
 estar determinado por un punto, una línea o un plano.
La geometría plana

11.  Términos no definidos
 En geometría los términos punto, recta y plano se
consideran términos no definidos, porque solo tienen
explicación a través del uso de ejemplos y descripciones.
Componentes básicos de la geometría

12.  Sin embargo, ellos sirven para definir otros
términos y propiedades geométricas. Puedes tomar
como referencia la definición de puntos colineales
(aquellos que yacen sobre la misma recta) para
definir puntos coplanares como aquellos que yacen
en el mismo plano.
Componentes básicos de la geometría

13.  Todos los puntos del plano cartesiano son coplanares.
Algunas veces se dificulta identificar puntos coplanares en el
espacio, a menos que entiendas la representación en un
dibujo.
Componentes básicos de la geometría

14. Punto
Un punto no tiene dimensión. Se representa con un pequeño punto.

15. Recta
Una recta tiene una sola dimensión. Se extiende indefinidamente en ambas
direcciones.

16. Plano
Un plano tiene dos dimensiones. Es una superficie plana que se extiende
indefinidamente en todas direcciones. El plano no tiene grosor.

17.  Postulado 1
 La intersección de dos rectas es un punto.
Postulados

18.  Postulado 2
 Tres puntos no colineales determinan exactamente un plano.
Cont.

19.  Colineal- puntos que yacen en la misma recta.
 Coplano- puntos que están en el mismo plano.
 Recta- Término primitivo en geometría. Las rectas se
extienden indefinidamente en ambos sentidos y no tienen
grosor ni ancho.
Glosario

20.  Rayo – parte de una recta que sólo tiene origen.
 Punto- Término primitivo en geometría. Los puntos no tienen
tamaño.
 Segmento- parte de una recta que consiste de dos puntos,
llamados extremos, y de todos los puntos que están entre ellos.
Glosario

21. Tipos de Ángulos
agudo recto

22. Tipos de Ángulos
obtuso llano

23.  La esquina de un ángulo se llama vértice
 Los lados rectos son rayos
 El ángulo es la cantidad entre los dos rayos.
Partes de un ángulo

24.  Una figura es bidimensional si tiene dos dimensiones,
por ejemplo, ancho y largo, pero no profundidad. Los
planos son bidimensionales, y sólo pueden contener
cuerpos unidimensionales o bidimensionales.
Figuras bidimensionales

25. Polígonos Regulares
Triangulo
 Tiene 3 lados y angulos
Cuadrilátero
 Tiene 4 lados y angulos

26. Polígonos Regulares
Pentágono
 Tiene 5 lados y angulos
Hexágono
 Tiene 6 lados y angulos

27.  Octágono
 Tiene 8 lados y angulos

28.  Área de un rectángulo
 A = bh
 El perimetro es la suma de todos sus lados.
Perímetro y área
Base
Altura

29.  Área de un triángulo
 El área de un triangulo es la mitad del producto de las
longitudes de la base y la altura
 Formula : A =
1
2
bh
Área de triángulos
h
b

30. ÁREAS Y PERÍMETROSDE LOS CUERPOS ELEMENTALES
TRIÁNGULO CUADRADO RECTÁNGULO
ROMBO TRAPECIO
CIRCUNFERENCIA
CÍRCULO

31. Fórmulas de Área y Perímetro
 Rectángulo
 Cuadrado
 Triángulo
A = ba
P = 2b + 2a
A = a2
P = 4a
A = ½ ba
P = b + c + d
a
a
a
b
b
cd

32. Área, Perímetro y Circunferencia
 Círculo
 Paralelogramo
 Rombo
 Trapecio
A = πr2
P = C = πd = 2rπ
A = ba
P = 2b + 2c
A = ba
P = 4b
A = ½ a (b + c)
P = b + c + d + e
r
a
b
c
b
a
a
b
c
d e

33. Cuadrado
P = a + a + a + a = c
P = 4a
Triángulo Equilátero
3 lados iguales
P = a + a + a
P = 3 x a = 3a
aa
a
a
a
a
a

34.  Área de un triángulo
 El área de un triangulo es la mitad del producto de las
longitudes de la base y la altura
 Formula : A =
1
2
bh
Área de triángulos
h
b

35. Triángulo Isósceles
2 lados iguales
P = a + a + b
P = 2 x a + b = 2(a) + b
aa
b
Triángulo Escaleno
3 lados distintos
P = a + b + c
ab
c

36. Área de un cuadrado
A = a x a a2
Área de un rectángulo
A = a x b a . b
a
a
a
a
a
a
bb

37.  Área de un rectángulo
 A = bh
 El perimetro es la suma de todos sus lados.
Perímetro y área
Base
Altura

38. 1 cm
2 cm
1 cm
6 cm
¿ Cómo calcularías el área ?

39.  http://www.math-aids.com/Geometry/Polygons/
 http://www.mathworksheets4kids.com/polygon.html
 http://www.greatschools.org/worksheets-activities/5646-
naming-polygons.gs
 http://www.commoncoresheets.com/Shapes.php
 http://edhelper.com/polygons.htm
 http://www.helpingwithmath.com/by_subject/geometry/g
eo_worksheets.htm
 http://nlvm.usu.edu/es/nav/vlibrary.html
Recursos en la web

40. Actividades

41.  Figuras geométricas en Word.
 Construir el plano cartesiano en Word.
 Construir figuras bidimensionales en el plano
cartesiano.
Instrucciones

42. 4
3
2
1
-4 -3 -2 0 1 2 3 4

43.  Presentación de la herramienta GeoGebra.
 Seguir las instrucciones del instructor
 Varias actividades con GeoGebra
GeoGebra