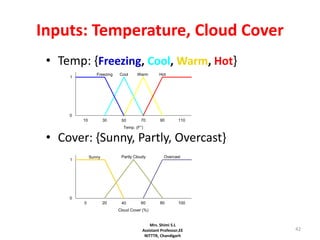
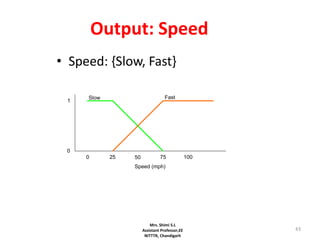
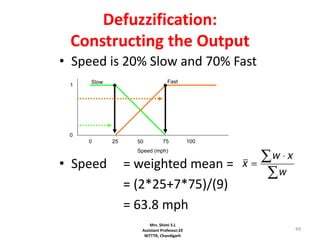
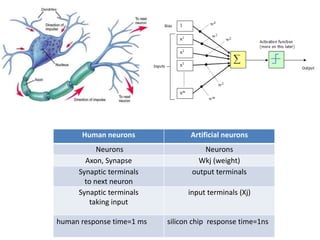
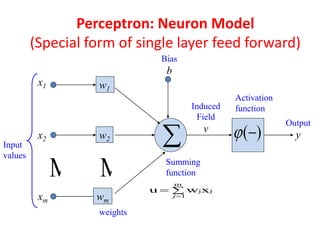
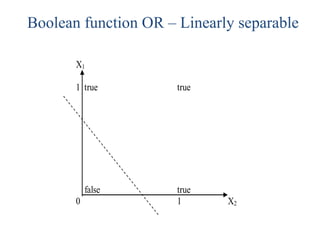
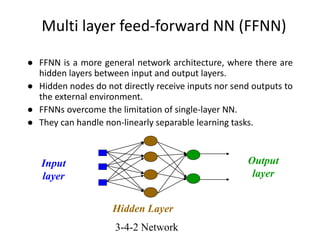
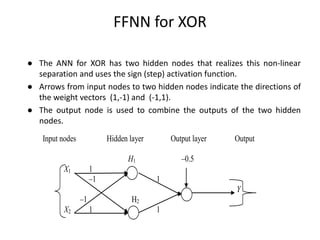
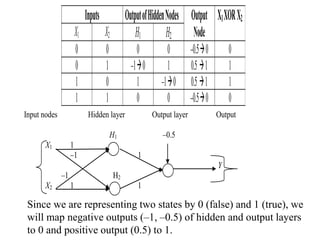
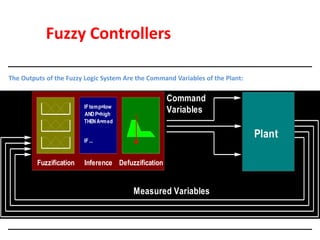
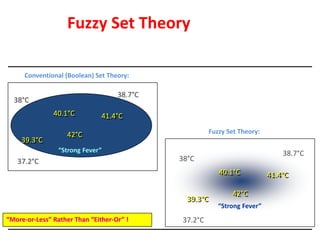
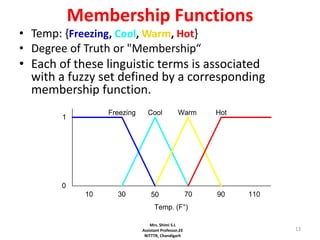
Fuzzy Logic and Neural Network

By
Mrs. Shimi S.L
Assistant Professor,EE
NITTTR, Chandigarh
Fuzzy Logic using MATLAB

The term "fuzzy logic" was introduced with
the 1965 proposal of fuzzy set
theory by Lotfi A. Zadeh.
Fuzzy logic is a form
of many-valued logic; it
deals with reasoning that is
approximate rather than
fixed and exact.
Mrs. Shimi S.L
NITTTR, Chandigarh

Fuzzy Controllers
The Outputs of the Fuzzy Logic System Are the Command Variables of the Plant:
Fuzzification Inference Defuzzification
IFtemp=low
ANDP=high
THENA=med
IF...
Variables
Measured Variables
Plant
Command

Conventional (Boolean) Set Theory:
Fuzzy Set Theory
“Strong Fever”
40.1°C
42°C
41.4°C
39.3°C
38.7°C
37.2°C
38°C
Fuzzy Set Theory:
40.1°C
42°C
41.4°C
39.3°C
38.7°C
37.2°C
38°C
“More-or-Less” Rather Than “Either-Or” !
“Strong Fever”

Fuzzy Set vs Crisp Set
• X is a set of all real numbers from 1 to 10
• Universe of Discourse
• A is a set of real numbers between 5 and 8
• Crisp or Classical Set
• Membership Value 1 or 0

Fuzzy Set vs Crisp Set
• B is a set of young people
• Membership values between 0 and 1 – Fuzzy Set
Age 65 27 17 32 22 25
B 0 0.3 1 0 0.8 0.5

Fuzzy Set
• Another example of Fuzzy
Set
• What season is it right now?
• Using the astronomical
definitions for season, we
get sharp boundaries.
• What we experience as
seasons varies more or less
continuously

Traditional Representation of Logic
Slow Fast
Speed = 0 Speed = 1
bool speed;
get the speed
if ( speed == 0) {
// speed is slow
}
else {
// speed is fast
}
Mrs. Shimi S.L
NITTTR, Chandigarh

Fuzzy Logic Representation
 Every problem must be
represent in terms of
fuzzy sets.
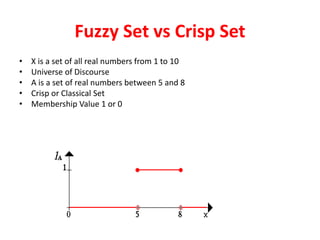
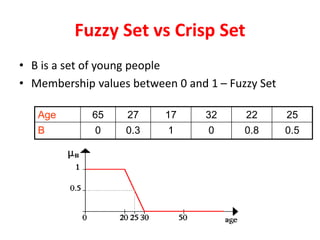
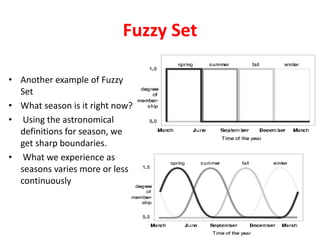
 What are fuzzy sets?
Slowest
Fastest
Slow
Fast
[ 0.0 – 0.25 ]
[ 0.25 – 0.50 ]
[ 0.50 – 0.75 ]
[ 0.75 – 1.00 ]

Fuzzy Logic Representation
Slowest Fastest
float speed;
get the speed
if ((speed >= 0.0)&&(speed < 0.25)) {
// speed is slowest
}
else if ((speed >= 0.25)&&(speed < 0.5))
{
// speed is slow
}
else if ((speed >= 0.5)&&(speed < 0.75))
{
// speed is fast
}
else // speed >= 0.75 && speed < 1.0
{
// speed is fastest
}
Slow Fast

12
Fuzzy Linguistic Variables
• Fuzzy Linguistic Variables are used to
represent qualities spanning a particular
spectrum
• Temp: {Freezing, Cool, Warm, Hot}
• Membership Function
• Question: What is the temperature?
• Answer: It is warm.
• Question: How warm is it?
Mrs. Shimi S.L
NITTTR, Chandigarh

13
Membership Functions
• Degree of Truth or "Membership“
• Each of these linguistic terms is associated
with a fuzzy set defined by a corresponding
membership function.
50 70 90 1103010
Temp. (F°)
Freezing Cool Warm Hot
0
1
Mrs. Shimi S.L
NITTTR, Chandigarh

• Membership function (MF) is a curve that defines
how each point in the input space is mapped to a
membership value (or degree of membership)
between 0 and 1 and is often given the designation
of µ.
• µA(x) is called the membership function (or MF) of x
in A.
• Thus membership functions are subjective measures
for linguistic terms.
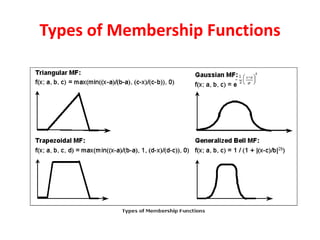
• There are many types of membership functions.

16
• How cool is 36 F° ?
50 70 90 1103010
Temp. (F°)
0
1
Mrs. Shimi S.L
NITTTR, Chandigarh

17
• How cool is 36 F° ?
• It is 30% Cool and 70% Freezing
50 70 90 1103010
Temp. (F°)
0
1
0.7
0.3
Mrs. Shimi S.L
NITTTR, Chandigarh

18
Fuzzy Logic
• How do we use fuzzy membership
functions in predicate logic?
• Fuzzy logic Connectives:
– Fuzzy Conjunction, 
– Fuzzy Disjunction, 
• Operate on degrees of membership
in fuzzy sets
Mrs. Shimi S.L
NITTTR, Chandigarh

19
Fuzzy Disjunction (Union)
• AB max(A, B)
• AB = C "Quality C is the
disjunction of Quality A and B"
0
1
0.375
A
0
1
0.75
B
(AB = C)  (C = 0.75)
Mrs. Shimi S.L
NITTTR, Chandigarh

20
Fuzzy Conjunction (Intersection)
• AB min(A, B)
• AB = C "Quality C is the
conjunction of Quality A and B"
0
1
0.375
A
0
1
0.75
B
(AB = C)  (C = 0.375)
Mrs. Shimi S.L
NITTTR, Chandigarh

Fuzzy Set Operations
• There are three basic operation on fuzzy sets: negation, intersection,
and union
• Negation
membership_value(not x)= 1- membership_value(x)
where x is the fuzzy set being negated
• Intersection
membership_value(x and y) = minimum{membership_value(x),
membership_value(y)}
where x and y are the fuzzy sets involved in the intersection
• Union
membership_value(x or y) = maximum{membership_value(x),
membership_value(y)}
where x and y are the fuzzy sets involved in the union
• minimum operator for intersection and the
maximum operator for union

• Let A be a fuzzy interval between 5 and 8
• B be a fuzzy number about 4.

Union of A and B
A OR B
Intersection of A and B
A AND B

• Negation of A • De Morgan’s Laws
BABA
BABA



100
0
80
0
40
0
20
40
10
70
1
1

..
A
100
0
80
20
40
50
20
01
10
01
1
30

.....
B
BABAvi
BABAv
Biv
Aiii
BAii
BAi




)(
)(
)(
)(
)(
)(

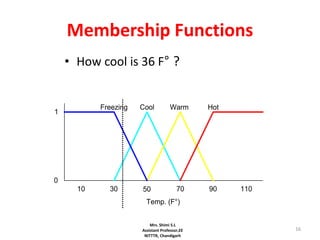
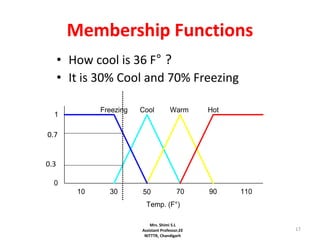
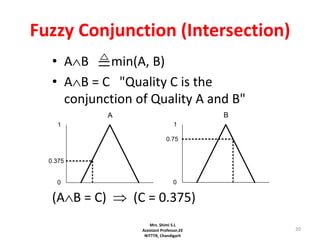
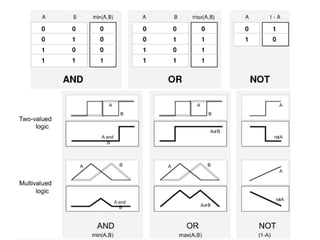
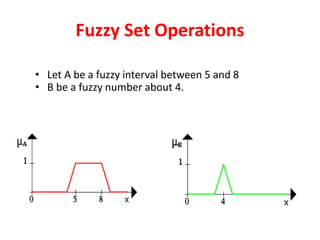
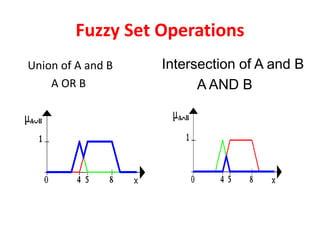
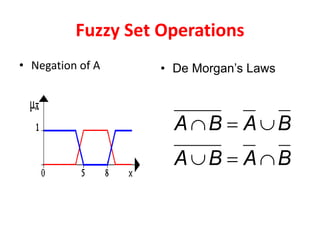
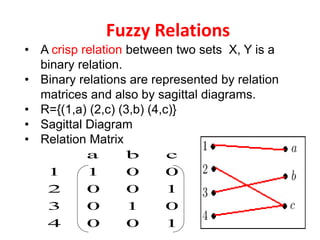
Fuzzy Relations
• A crisp relation between two sets X, Y is a
binary relation.
• Binary relations are represented by relation
matrices and also by sagittal diagrams.
• R={(1,a) (2,c) (3,b) (4,c)}
• Sagittal Diagram
• Relation Matrix
1004
0103
1002
0011
cba

Fuzzy Relations
• Relation between two or more fuzzy sets is
obtained by the Cartesian product.
        yxyxyx BAAxBR  ,min,, 
321 x
1
+
x
50
+
x
20
=A
..
21 y
90
+
y
30
=B
..
9030x
5030x
2020x
yy
3
2
1
21
..
..
..

Fuzzy Relations
• Let us describe the relationship between the
colour of a fruit, x and the grade of maturity, y.
• x= {green, yellow, red}
y={verdant, half-mature, mature}
• Considering the relation between the linguistic
terms red and mature, and representing them
by the membership functions, a fruit can be
characterized by the property of red and
mature.

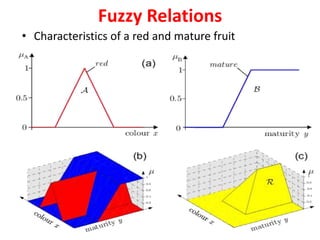
Fuzzy Relations
• Characteristics of a red and mature fruit

4.08.0
5.07.0=
2
1
21
x
x
yy
R
Fuzzy Compositions
T = R o S - max-min composition
T = R S - max-product composition
Chain-strength analogy for max-min composition
5.07.01.0
2.06.09.0=
2
1
321
y
y
zzz
S
( ) ( ) ( )( ){ }zyyxzx SRT ,,,minmax=, 
( ) ( ) ( )( ){ }zyyxzx SRT ,•,max=, 

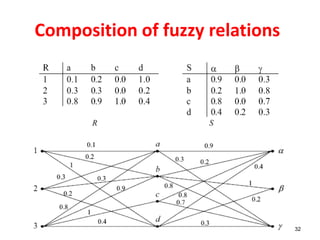
32
Composition of fuzzy relations

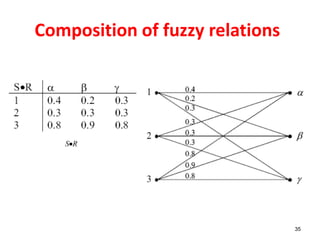
33
• Example
(1, ) max[min(0.1,0.9),min(0.2,0.2),min(0.0,0.8),min(1.0,0.4)]
max[0.1,0.2,0.0,0.4] 0.4
S R  
 
g

34
• Example
(1, ) max[min(0.1,0.0),min(0.2,1.0),min(0.0,0.0),min(1.0,0.2)]
max[0.0,0.2,0.0,0.2] 0.2
S R  
 
g

35

Fuzzy Relations
• Three variables of interest in power transistors are the
amount of current that can be switched, the voltage that can
be switched, and the cost. The following membership
functions for power transistors were developed from
hypothetical components catalog:
• Average current
• Average voltage
• Power is defined by the algebraic operation P = VI
(a) Let us find the Cartesian Product P = VxI.
{ }
21
60
+
11
80
+
1
1
+
90
70
+
80
40
=
.
.
.
.
.
.
.
.
I
{ }
90
70
+
75
90
+
60
1
+
45
80
+
30
20
=
....
V

Fuzzy Relations
• The Cartesian Product expresses the relationship between
Vi and Ij , where Vi and Ij are individual elements in the
fuzzy set V and I.
• Now let us define a fuzzy set for the cost C in rupees, of a
transistor
(b)Using a fuzzy Cartesian Product, find T = IxC.
(c) Using max-min composition find E = PoT
(d) Using max-product composition find E = PoT
{ }
70
50
+
60
1
+
50
40
=
.
.
..
.
C

Fuzzy Control
Using a procedure originated by Ebrahim Mamdani
in the late 70s, three steps are taken to create a
fuzzy controlled machine:
 Fuzzification (Using membership functions to
graphically describe a situation)
 Rule Evaluation (Application of fuzzy rules)
 Defuzzification (Obtaining the crisp results)

Fuzzy Control
 Fuzzification is the process of making a crisp quantity
fuzzy.
 Membership functions characterize the fuzziness in a
fuzzy set.
 Six procedures to build membership functions
Intuition
Inference
Rank Ordering
Neural Networks
Genetic Algorithm
Inductive Reasoning

Fuzzy Control
 Defuzzification is the conversion of a fuzzy quantity to a
precise quantity.
 Output of a fuzzy process can be the logical union of two or
more fuzzy membership functions defined on the universe of
discourse. .
 Methods of defuzzification
Max-membership principle
Centroid method
Weighted average method
Mean max membership
Center of sums
Center of largest area
First (or last) of maxima

41
Fuzzy Control
• Fuzzy Control combines the use of
fuzzy linguistic variables with fuzzy
logic
• Example: Speed Control
• How fast am I going to drive today?
• It depends on the weather.
• Disjunction of Conjunctions
Mrs. Shimi S.L
NITTTR, Chandigarh

42
Inputs: Temperature, Cloud Cover
• Cover: {Sunny, Partly, Overcast}
50 70 90 1103010
Temp. (F°)
0
1
40 60 80 100200
Cloud Cover (%)
OvercastPartly CloudySunny
0
1
Mrs. Shimi S.L
NITTTR, Chandigarh

43
Output: Speed
• Speed: {Slow, Fast}
50 75 100250
Speed (mph)
Slow Fast
0
1
Mrs. Shimi S.L
NITTTR, Chandigarh

44
Rules
• If it's Sunny and Warm, drive Fast
Sunny(Cover)Warm(Temp) Fast(Speed)
• If it's Cloudy and Cool, drive Slow
Cloudy(Cover)Cool(Temp) Slow(Speed)
• Driving Speed is the combination of
output of these rules...
Mrs. Shimi S.L
NITTTR, Chandigarh

45
Example Speed Calculation
• How fast will I go if it is
– 65 F°
– 25 % Cloud Cover ?
Mrs. Shimi S.L
NITTTR, Chandigarh

46
Fuzzification:
Calculate Input Membership Levels
• 65 F°  Cool = 0.4, Warm= 0.7
• 25% Cover Sunny = 0.8, Cloudy = 0.2
50 70 90 1103010
Temp. (F°)
0
1
40 60 80 100200
Cloud Cover (%)
OvercastPartly CloudySunny
0
1
Mrs. Shimi S.L
NITTTR, Chandigarh

47
...Calculating...
• If it's Sunny and Warm, drive Fast
Sunny(Cover)Warm(Temp)Fast(Speed)
0.8  0.7 = 0.7
 Fast = 0.7
• If it's Cloudy and Cool, drive Slow
Cloudy(Cover)Cool(Temp)Slow(Speed)
0.2  0.4 = 0.2
 Slow = 0.2
AB = min(A, B)
Mrs. Shimi S.L
NITTTR, Chandigarh

48
Defuzzification:
Constructing the Output
• Speed is 20% Slow and 70% Fast
• Find centroids: Location where
membership is 100%
50 75 100250
Speed (mph)
Slow Fast
0
1
Mrs. Shimi S.L
NITTTR, Chandigarh

49
Defuzzification:
Constructing the Output
• Speed is 20% Slow and 70% Fast
• Speed = weighted mean =
= (2*25+7*75)/(9)
= 63.8 mph
50 75 100250
Speed (mph)
Slow Fast
0
1
Mrs. Shimi S.L
NITTTR, Chandigarh

● Artificial neural network (ANN) is a machine
learning approach that models human brain and
consists of a number of artificial neurons.
● An Artificial Neural Network is specified by:
− neuron model: the information processing unit
of the NN,
− an architecture: a set of neurons and links
connecting neurons. Each link has a weight,
− a learning algorithm: used for training the NN
by modifying the weights in order to model a
particular learning task correctly on the
training examples.
● The aim is to obtain a NN that is trained and
generalizes well.
● It should behaves correctly on new instances of
the learning task.

The Biological Neural Network
Characteristics of Human Brain
• Ability to learn from experience
• Ability to generalize the knowledge it possess
• Ability to perform abstraction
• To make errors.

• A neuron fires when the sum of its collective
inputs reaches a threshold
• There are about 10^11 neurons per person
• Each neuron may be connected with up to
10^5 other neurons
Consists of three
sections
cell body
dendrites
axon

• Nerve impulses which pass down the axon, jump
from node to node, thus saving energy.
• There are about 10^16 synapses. Usually no
physical or electrical connection made at the
synapse.

Human neurons Artificial neurons
Neurons Neurons
Axon, Synapse Wkj (weight)
Synaptic terminals
to next neuron
output terminals
Synaptic terminals
taking input
input terminals (Xj)
human response time=1 ms silicon chip response time=1ns

Input
values
weights
Summing
function
Bias
b
Activation
functionInduced
Field
v
Output
y
x1
x2
xm
w2
wm
w1
 
 )(


m
1
jjxwu
j
Perceptron: Neuron Model
(Special form of single layer feed forward)

Neuron
● The neuron is the basic information processing unit of a
NN. It consists of:
1 A set of links, describing the neuron inputs, with weights W1, W2,
…, Wm
2 An adder function (linear combiner) for computing the weighted
sum of the inputs:
(real numbers)
3 Activation function for limiting the amplitude of the neuron
output. Here ‘b’ denotes bias.


m
1
jjxwu
j

)(uy b

Bias of a Neuron
● The bias b has the effect of applying a transformation to
the weighted sum u
v = u + b
● The bias is an external parameter of the neuron. It can be
modeled by adding an extra input.
● v is called induced field of the neuron
bw
xwv j
m
j
j

 
0
0

Activation Function
● The choice of activation function determines the
neuron model.
Examples:
● step function:
● ramp function:
● sigmoid function with z,x,y parameters
● Gaussian function:














 

2
2
1
exp
2
1
)(




v
v
)exp(1
1
)(
yxv
zv











otherwise))/())(((
if
if
)(
cdabcva
dvb
cva
v






cvb
cva
v
if
if
)(

Training
Training is accomplished by sequentially applying input vectors while
adjusting network weights according to a predetermined procedures.
Supervised Training
requires the pairing of each input vector with a target vector representing
the desired output.
Unsupervised Training
requires no target vector for the output and no comparisons to
predetermined ideal responses. The training algorithm modifies network
weights to produce output vectors that are consistent. Also called self-
organizing networks.

Gradient descent or Steepest Descent
ɳ is the learning rate
global minimum

X1
1 true true
false true
0 1 X2
Boolean function OR – Linearly separable

These two classes (true and false) cannot be separated using a
line. Hence XOR is non linearly separable.
Input Output
X1 X2 X1 XOR X2
0 0 0
0 1 1
1 0 1
1 1 0
X1
1 true false
false true
0 1 X2

Multi layer feed-forward NN (FFNN)
● FFNN is a more general network architecture, where there are
hidden layers between input and output layers.
● Hidden nodes do not directly receive inputs nor send outputs to
the external environment.
● FFNNs overcome the limitation of single-layer NN.
● They can handle non-linearly separable learning tasks.
Input
layer
Output
layer
Hidden Layer
3-4-2 Network

FFNN for XOR
● The ANN for XOR has two hidden nodes that realizes this non-linear
separation and uses the sign (step) activation function.
● Arrows from input nodes to two hidden nodes indicate the directions of
the weight vectors (1,-1) and (-1,1).
● The output node is used to combine the outputs of the two hidden
nodes.
Input nodes Hidden layer Output layer Output
H1 –0.5
X1 1
–1 1
Y
–1 H2
X2 1 1

Inputs OutputofHiddenNodes Output
Node
X1XORX2
X1 X2 H1 H2
0 0 0 0 –0.50 0
0 1 –10 1 0.5 1 1
1 0 1 –10 0.5 1 1
1 1 0 0 –0.50 0
Since we are representing two states by 0 (false) and 1 (true), we
will map negative outputs (–1, –0.5) of hidden and output layers
to 0 and positive output (0.5) to 1.
Input nodes Hidden layer Output layer Output
H1 –0.5
X1 1
–1 1
Y
–1 H2
X2 1 1

Hardware Implementation
• Dspace
• Quad-Core AMD
Opteron processor

72
Thank you.
Questions, Comments, …?
Shimi.reji@gmail.com
9417588987

• Human can identify a person through thoughts.which means humans neurons are getting trained
itself. Therefore through Artificial Neural Network we can train artificial neurons using computer
programming . using neural network we are trying to build a network between neurons to transfer
the electrical signals.which are consists of neural commands .
• usually Computer response time is 10^6 times faster than humans response time because of the
silicon Integrated chips.
• silicon chip response time :- 1 nanosecond
• human response time :- 1 millisecond
•
• but human can perform faster than chips because human has massively parallel neural structure. If
we consider human neuron structure it has synaptic terminals, cell body(neurons), basal dendrite
and axon. Each components has some function to transfer signal to
neurons.

• Bias neurons are added to neural networks to
help them learn patterns. A bias neuron is
nothing more than a neuron that has a
constant output of one. Because the bias
neurons have a constant output of one they
are not connected to the previous layer. The
value of one, which is called the bias
activation, can be set to values other than
one. However, one is the most common bias
activation.

Fuzzy Logic and Neural Network

More Related Content

What's hot

Similar to Fuzzy Logic and Neural Network

More from SHIMI S L

Recently uploaded

Fuzzy Logic and Neural Network