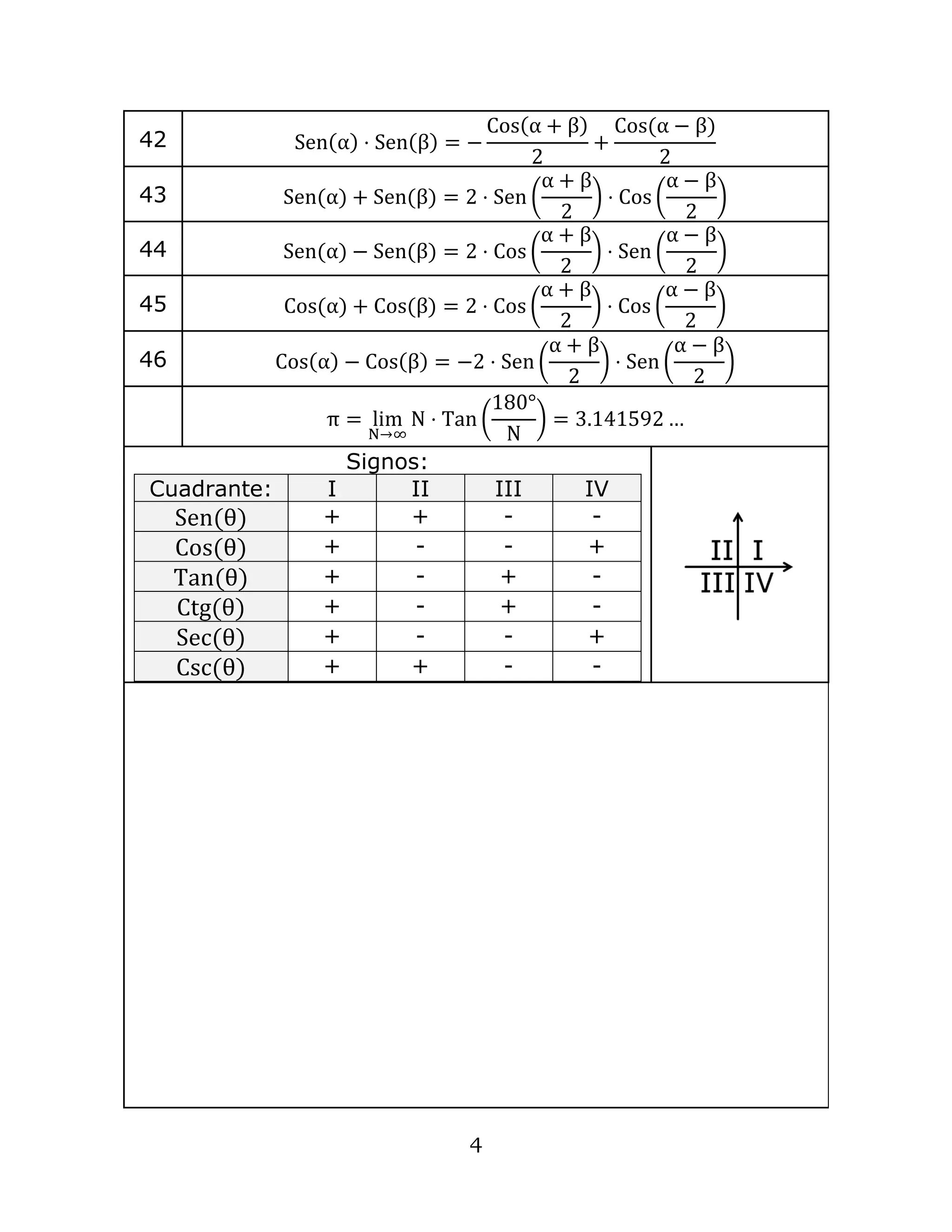
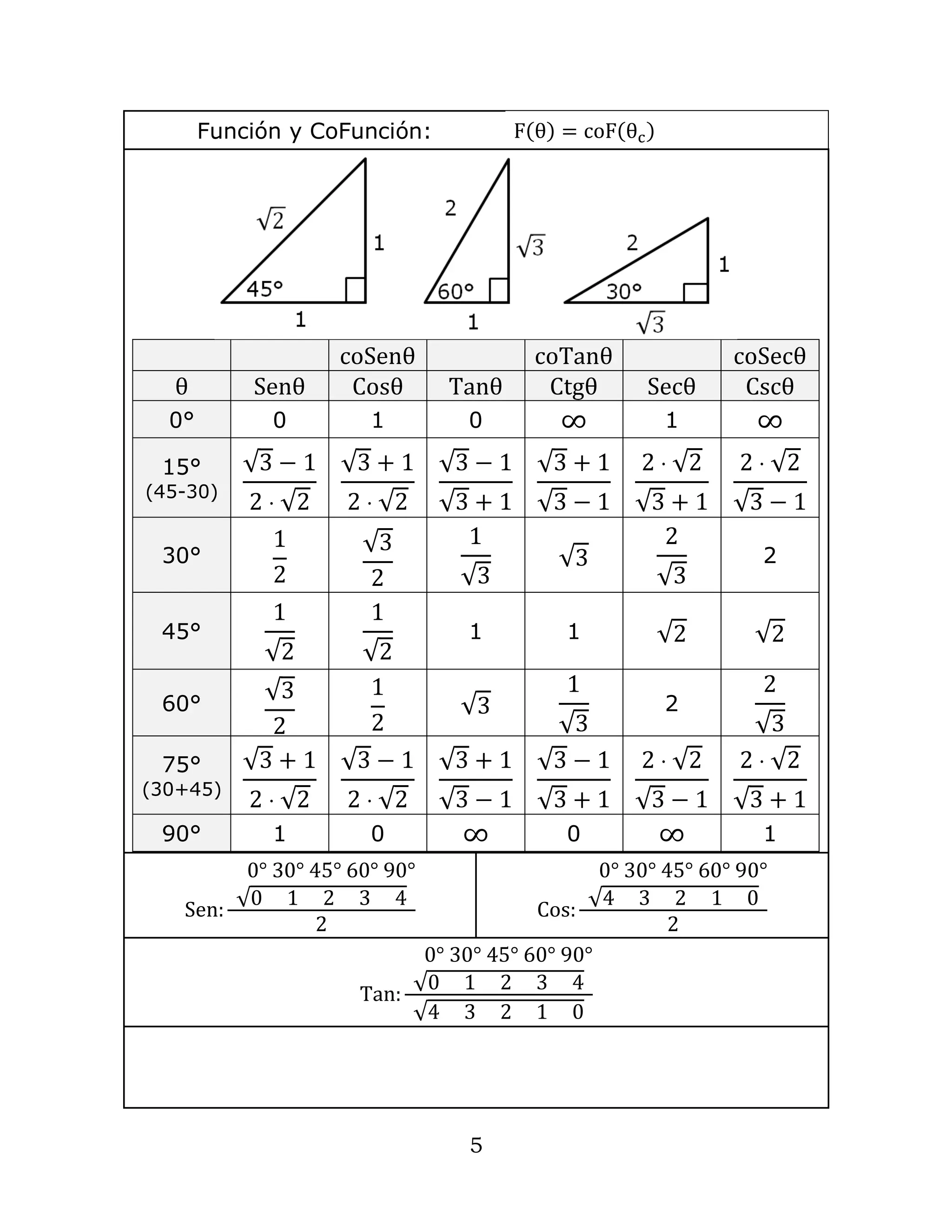
1. The document contains formulas and definitions related to trigonometry, including definitions of trigonometric functions, identities, right triangles, laws of sines and cosines for oblique triangles, trigonometric functions of vectors, and hyperbolic trigonometry. 2. Key concepts covered include definitions of trigonometric functions, complementary and supplementary angles, trigonometric ratios in right triangles, trigonometric identities, laws of sines and cosines, vector dot and cross products, and hyperbolic trigonometric functions. 3. The document provides over 75 formulas and definitions in both text and mathematical notation to comprehensively cover topics in plane and vector trigonometry.

1. 1
FORMULARIO DE TRIGONOMETRÍA
01 S = θ ⋅ R
1Rad =
360°
2 ⋅ π
1Rad = 57.3°
02
Complementarios
03
Suplementarios
04
Conjugados
θ + θc = 90° θ + θs = 180° θ + θk = 360°
TRIÁNGULOS RECTÁNGULOS
05 h2
= co2
+ ca2
06 A =
B ⋅ H
2
B = Base = ca
H = Altura = co
R = OB
̅̅̅̅ = OC
̅̅̅̅ = OE
̅̅̅̅
07 AB
̅̅̅̅ = Sen(θ) =
co
h
=
1
Csc(θ)
08 OA
̅̅̅̅ = Cos(θ) =
ca
h
=
1
Sec(θ)
09 CD
̅̅̅̅ = Tan(θ) =
co
ca
=
1
Ctg(θ)
=
Sen(θ)
Cos(θ)
10 EF
̅
̅̅
̅ = Ctg(θ) =
ca
co
=
1
Tan(θ)
=
Cos(θ)
Sen(θ)
11 OD
̅̅̅̅ = Sec(θ) =
h
ca
=
1
Cos(θ)
12 OF
̅̅̅̅ = Csc(θ) =
h
co
=
1
Sen(θ)
Si θ ≅ 0 Rad ⇒ {
BC
̅̅̅̅ ≅ AB
̅̅̅̅ ≅ CD
̅̅̅̅
S ≅ Sen(θ) ≅ Tan(θ)
13 ⊿OAB: Sen2
(θ) + Cos2
(θ) = 1 Sen(−θ) = −Sen(θ)
Cos(−θ) = Cos(θ)
Tan(−θ) = −Tan(θ)
14 ⊿OCD: Tan2
(θ) + 1 = Sec2
(θ)
15 ⊿OEF: 1 + Ctg2
(θ) = Csc2
(θ)

2. 2
16 θ = ω ⋅ t
{
x = Cos(t)
y = Sen(t)
x2
+ y2
= 1
17 {
x = Cos(ω ⋅ t)
y = Sen(ω ⋅ t)
18 x2
+ y2
= 1
19 Sen(θ) = θ −
θ3
6
+
θ5
120
−
θ7
5040
+ ⋯
20 Cos(x) = 1 −
θ2
2
+
θ4
24
−
θ6
720
+ ⋯
TRIÁNGULOS OBLICUÁNGULOS
21 α + β + γ = 180°
22
Ley de Senos:
a
Sen(α)
=
b
Sen(β)
=
c
Sen(γ)
= 2 ⋅ Rc
23
Ley de Cosenos:
a2
= b2
+ c2
− 2 ⋅ b ⋅ c ⋅ Cos(α)
b2
= a2
+ c2
− 2 ⋅ a ⋅ c ⋅ Cos(β)
c2
= a2
+ b2
− 2 ⋅ a ⋅ b ⋅ Cos(γ)
24
Ley de Cosenos:
α = ∢Cos (
a2
− b2
− c2
−2 ⋅ b ⋅ c
)
β = ∢Cos (
b2
− a2
− c2
−2 ⋅ a ⋅ c
)
γ = ∢Cos (
c2
− a2
− b2
−2 ⋅ a ⋅ b
)
25
Ley de las Proyecciones:
a = b ⋅ Cos(γ) + c ⋅ Cos(β)
b = a ⋅ Cos(γ) + c ⋅ Cos(α)
c = a ⋅ Cos(β) + b ⋅ Cos(α)

3. 3
26
Ri = (
−a + b + c
2
) ⋅ Tan (
α
2
)
Ri = (
a − b + c
2
) ⋅ Tan (
β
2
)
Ri = (
a + b − c
2
) ⋅ Tan (
γ
2
)
(06) A =
B ⋅ H
2
27 A =
a ⋅ b
2
⋅ Sen(γ) =
a ⋅ c
2
⋅ Sen(β) =
b ⋅ c
2
⋅ Sen(α)
28 A =
1
4
⋅ √(a + b + c) ⋅ (−a + b + c) ⋅ (a − b + c) ⋅ (a + b − c)
IDENTIDADES TRIGONOMÉTRICAS
29
Identidades Trigonométricas Pitagóricas:
Sen2
(θ) + Cos2
(θ) = 1
Tan2
(θ) + 1 = Sec2
(θ)
1 + Ctg2
(θ) = Csc2
(θ)
30 Sen(α + β) = Sen(α) ⋅ Cos(β) + Cos(α) ⋅ Sen(β)
31 Sen(α − β) = Sen(α) ⋅ Cos(β) − Cos(α) ⋅ Sen(β)
32 Cos(α + β) = Cos(α) ⋅ Cos(β) − Sen(α) ⋅ Sen(β)
33 Cos(α − β) = Cos(α) ⋅ Cos(β) + Sen(α) ⋅ Sen(β)
34 Tan(α + β) =
Tan(α) + Tan(β)
1 − Tan(α) ⋅ Tan(β)
35 Tan(α − β) =
Tan(α) − Tan(β)
1 + Tan(α) ⋅ Tan(β)
36 Sen(2 ⋅ α) = 2 ⋅ Sen(α) ⋅ Cos(α)
37 Cos(2 ⋅ α) = Cos2
(α) − Sen2
(α)
38 Tan(2 ⋅ α) =
2 ⋅ Tan(α)
1 − Tan2(α)
39 Sen(α) ⋅ Cos(β) =
Sen(α + β)
2
+
Sen(α − β)
2
40 Cos(α) ⋅ Sen(β) =
Sen(α + β)
2
−
Sen(α − β)
2
41 Cos(α) ⋅ Cos(β) =
Cos(α + β)
2
+
Cos(α − β)
2

4. 4
42 Sen(α) ⋅ Sen(β) = −
Cos(α + β)
2
+
Cos(α − β)
2
43 Sen(α) + Sen(β) = 2 ⋅ Sen (
α + β
2
) ⋅ Cos (
α − β
2
)
44 Sen(α) − Sen(β) = 2 ⋅ Cos (
α + β
2
) ⋅ Sen (
α − β
2
)
45 Cos(α) + Cos(β) = 2 ⋅ Cos (
α + β
2
) ⋅ Cos (
α − β
2
)
46 Cos(α) − Cos(β) = −2 ⋅ Sen (
α + β
2
) ⋅ Sen (
α − β
2
)
π = lim
N→∞
N ⋅ Tan (
180°
N
) = 3.141592 …
Signos:
Cuadrante: I II III IV
Sen(θ) + + - -
Cos(θ) + - - +
Tan(θ) + - + -
Ctg(θ) + - + -
Sec(θ) + - - +
Csc(θ) + + - -

5. 5
Función y CoFunción: F(θ) = coF(θc)
coSenθ coTanθ coSecθ
θ Senθ Cosθ Tanθ Ctgθ Secθ Cscθ
0° 0 1 0 ∞ 1 ∞
15°
(45-30)
√3 − 1
2 ⋅ √2
√3 + 1
2 ⋅ √2
√3 − 1
√3 + 1
√3 + 1
√3 − 1
2 ⋅ √2
√3 + 1
2 ⋅ √2
√3 − 1
30°
1
2
√3
2
1
√3
√3
2
√3
2
45°
1
√2
1
√2
1 1 √2 √2
60°
√3
2
1
2
√3
1
√3
2
2
√3
75°
(30+45)
√3 + 1
2 ⋅ √2
√3 − 1
2 ⋅ √2
√3 + 1
√3 − 1
√3 − 1
√3 + 1
2 ⋅ √2
√3 − 1
2 ⋅ √2
√3 + 1
90° 1 0 ∞ 0 ∞ 1
Sen:
0° 30° 45° 60° 90°
√0 1 2 3 4
2
Cos:
0° 30° 45° 60° 90°
√4 3 2 1 0
2
Tan:
0° 30° 45° 60° 90°
√0 1 2 3 4
√4 3 2 1 0

6. 6
TRIGONOMETRÍA HIPERBÓLICA
47 Senh(x) =
℮x
− ℮−x
2
48 Cosh(x) =
℮x
+ ℮−x
2
49 Tanh(x) =
℮x
− ℮−x
℮x + ℮−x
=
Senh(x)
Cosh(x)
50 Ctgh(x) =
℮x
+ ℮−x
℮x − ℮−x
=
Cosh(x)
Senh(x)
=
1
Tanh(x)
x ≠ 0
51 Sech(x) =
2
℮x + ℮−x
=
1
Cosh(x)
52 Csch(x) =
2
℮x − ℮−x
=
1
Senh(x)
x ≠ 0
53 Si: y = Senh(x) =
℮x
− ℮−x
2
⇒ x = invSenh(y) = Ln (y + √y2 + 1)
54
Cosh2
(x) − Senh2
(x) = 1
1 − Tanh2
(x) = Sech2
(x)
Ctgh2
(x) − 1 = Csch2
(x)
{
x = Cosh(t)
y = Senh(t)
x2
− y2
= 1
55
Senh(−x) = −Senh(x)
Cosh(−x) = Cosh(x)
Tanh(−x) = −Tanh(x)
56 invSenh(x) = Ln (x + √x2 + 1)
57 invCosh(x) = Ln (x + √x2 − 1) x ≥ 1
58 invTanh(x) =
1
2
⋅ Ln (
1 + x
1 − x
) x2
< 1
59 invCtgh(x) =
1
2
⋅ Ln (
x + 1
x − 1
) x2
> 1
60 invSech(x) = Ln (
1 + √1 − x2
x
) 0 < x ≤ 1

7. 7
61 invCsch(x) = Ln (
1
x
+
√x2 + 1
|x|
) x ≠ 0
℮ = lim
N→∞
(1 +
1
N
)
N
= 2.718281 …
TRIGONOMETRÍA VECTORIAL
62 A
⃗
⃗ = (ax, ay, az) 63 A
⃗
⃗ = ax ⋅ î + ay ⋅ ĵ + az ⋅ k
̂
64 |A
⃗
⃗ | = √ax
2 + ay
2 + az
2 65 {
î = (1,0,0)
ĵ = (0,1,0)
k
̂ = (0,0,1)
66
Cosenos Directores.
{
Cos(αx) =
ax
|A
⃗
⃗ |
Cos(αy) =
ay
|A
⃗
⃗ |
Cos(αz) =
az
|A
⃗
⃗ |
68
Vector Unitario.
A
̂ =
A
⃗
⃗
|A
⃗
⃗ |
A
̂ =
(ax, ay, az)
|A
⃗
⃗ |
A
̂ = (
ax
|A
⃗
⃗ |
,
ay
|A
⃗
⃗ |
,
az
|A
⃗
⃗ |
)
67 Cos2(αx) + Cos2
(αy) + Cos2(αz) = 1
69
Producto PUNTO.
A
⃗
⃗ ⊡ B
⃗
⃗ = (ax, ay, az) ⊡ (bx, by, bz) = {
ax ⋅ bx + ay ⋅ by + az ⋅ bz
|A
⃗
⃗ | ⋅ |B
⃗
⃗ | ⋅ Cos(γ)
70
Producto CRUZ.
A
⃗
⃗ ⊠ B
⃗
⃗ = (ax, ay, az) ⊠ (bx, by, bz) = [
î ĵ k
̂
ax ay az
bx by bz
]
71 |A
⃗
⃗ ⊠ B
⃗
⃗ | = |A
⃗
⃗ | ⋅ |B
⃗
⃗ | ⋅ Sen(γ)
72 Area =
|A
⃗
⃗ ⊠ B
⃗
⃗ |
2
=
|A
⃗
⃗ | ⋅ |B
⃗
⃗ | ⋅ Sen(γ)
2

8. 8
73
Producto Mixto.
Volumen = (A
⃗
⃗ ⊠ B
⃗
⃗ ) ⊡ C
⃗
Volumen = [
ax ay az
bx by bz
cx cy cz
]
74
|A
⃗
⃗ ⊠ B
⃗
⃗ |
A
⃗
⃗ ⊡ B
⃗
⃗
= Tan(γ)
75
Proyección (o componente) de A
⃗
⃗ sobre B
⃗
⃗ .
A
⃗
⃗ B = (A
⃗
⃗ ⊡ B
̂) ⋅ B
̂
Elaboró: MCI José A. Guasco.
https://www.slideshare.net/AntonioGuasco1/