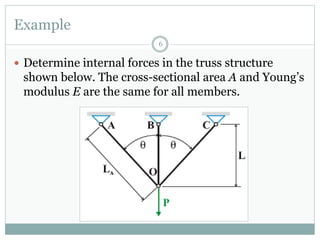
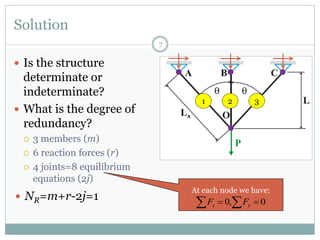
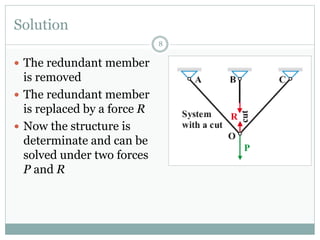
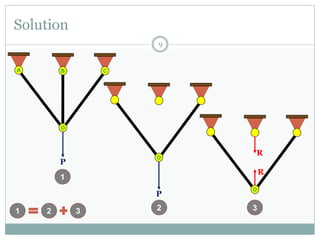
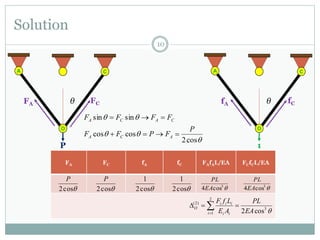
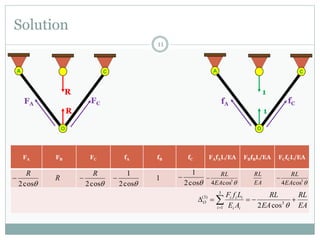
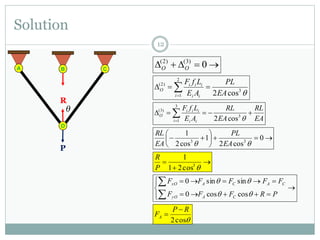
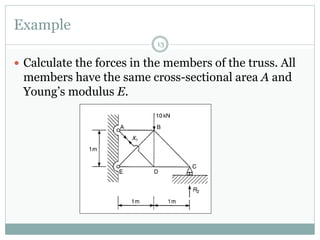
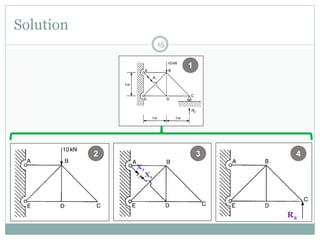
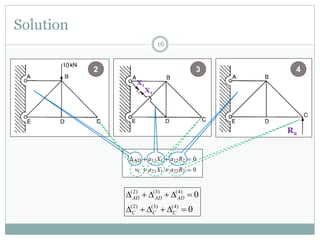
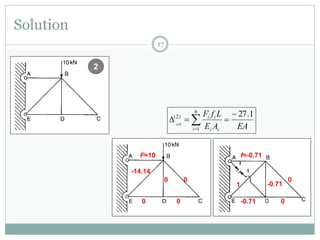
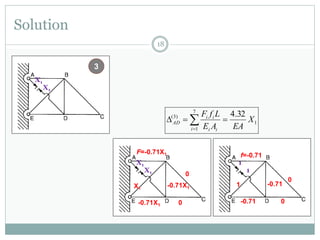
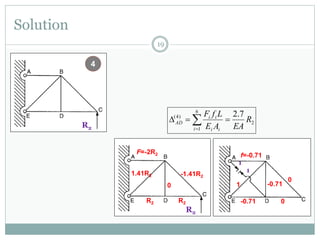
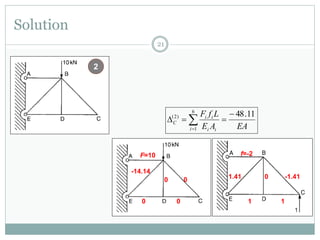
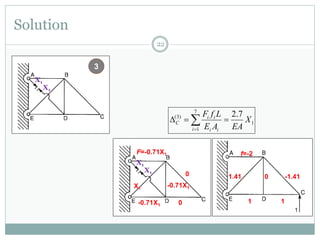
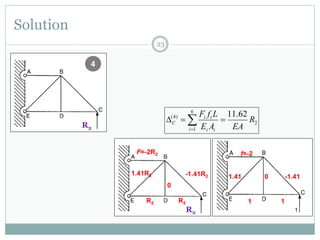
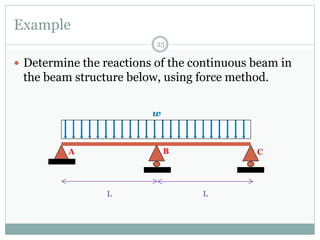
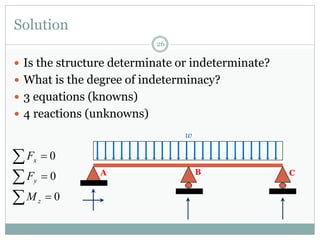
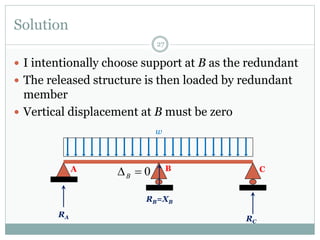
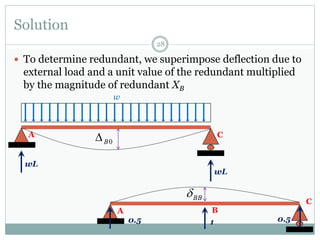
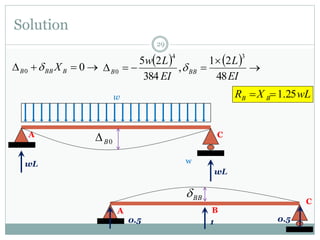
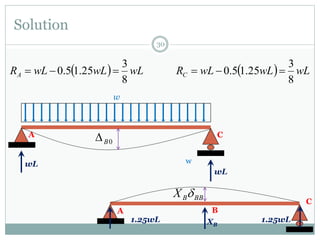
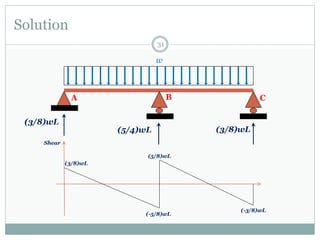
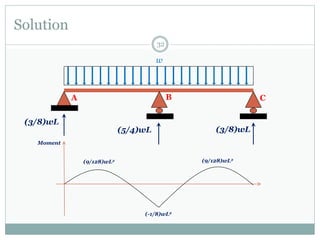
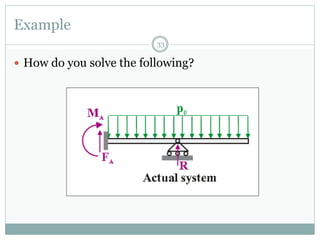
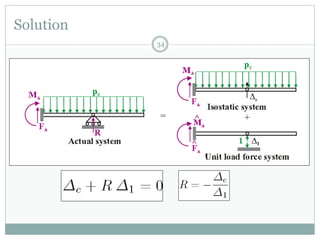
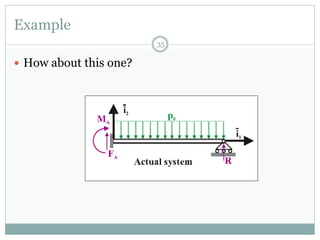
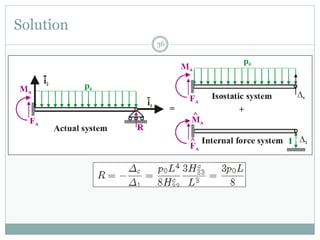
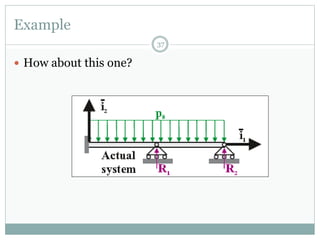
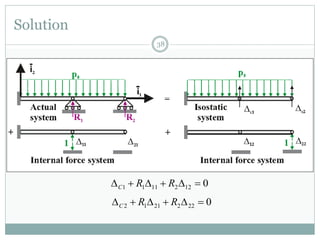
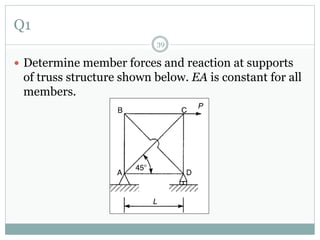
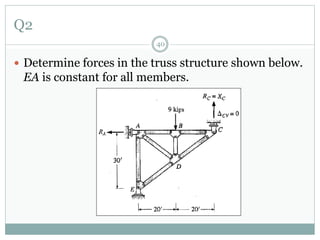
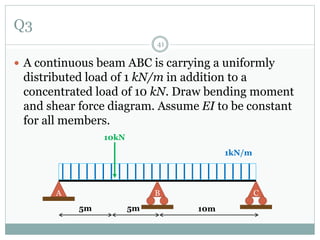
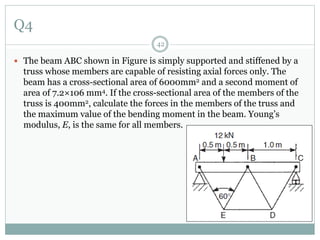
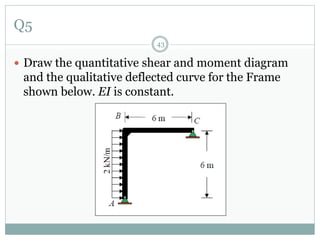
The first question asks to determine member forces in a provided truss structure using the force method. The second asks to do the same for a different truss. The third involves drawing bending moment and shear force diagrams for a continuous beam with distributed

1. B Y
D R . M A H D I D A M G H A N I
2 0 1 6 - 2 0 1 7
Structural Design and
Inspection-Energy method
1

2. Suggested Readings
Reference 1 Reference 2
2

3. Objective(s)
 Familiarisation with force method (flexibility
method)
 Ability to solve indeterminate structures
3

4. Introduction
 Refer to chapter 5 of Reference 1
 Refer to chapter 4 of Reference 2
 This method is for solving indeterminate structures
 Focuses on the solution for the system internal forces
 In this method the governing equations express
compatibility requirements in terms of the
redundant forces and component flexibilities
 Forces are determined first and then strains and
displacements are found
4

5. Procedure
 This method is also
called force method
because:
 Internal forces are found
first
 Then displacements and
strains are calculated
1
• Determine degree of redundancy of
the structure (NR)
2
• Remove NR members of the structure
3
• Represent each removed member by
its associated force
4
• Calculate displacement for each force
using unit load method
5
• Apply compatibility of displacements
6
• Solve a set of linear equations to
calculate redundant forces
7
• Calculate displacements and strains
 Let’s see this in some
examples
5

6. Example
 Determine internal forces in the truss structure
shown below. The cross-sectional area A and Young’s
modulus E are the same for all members.
6

7. Solution
7
 Is the structure
determinate or
indeterminate?
 What is the degree of
redundancy?
 3 members (m)
 6 reaction forces (r)
 4 joints=8 equilibrium
equations (2j)
 NR=m+r-2j=1
At each node we have:
  0,0 yx FF
1 2 3

8. Solution
8
 The redundant member
is removed
 The redundant member
is replaced by a force R
 Now the structure is
determinate and can be
solved under two forces
P and R

9. Solution
9
A B C
O
P
P
O
O
R
R
1
2 31 32

10. Solution
10
FA FC fA fC FAfAL/EA FCfCL/EA
P
A C
O
FCFA θ
cos2
P
cos2
P
cos2
1
cos2
1
3
cos4EA
PL
3
cos4EA
PL
3
2
1
)2(
cos2EA
PL
AE
LfF
i ii
iii
O  
1
A C
O
fCfA θ



cos2
coscos
sinsin
P
FPFF
FFFF
ACA
CACA



11. Solution
11
FA FB FC fA fB fC FAfAL/EA FBfBL/EA FCfCL/EA
cos2
R

cos2
1

3
cos4EA
RL

3
cos4EA
RL

EA
RL
EA
RL
AE
LfF
i ii
iii
O   3
3
1
)3(
cos2
cos2
R

A C
O
R
R
FCFA
A C
O
1
1
fCfA
1
cos2
1

EA
RL
R

12. Solution
12
 0)3()2(
OO






 0
cos2
1
cos2
1
33
 EA
PL
EA
RL
A B C
O
P
R
θ



3
cos21
1
P
R









PRFFF
FFFFF
CAyO
CACAxO


coscos0
sinsin0
cos2
RP
FA


3
2
1
)2(
cos2EA
PL
AE
LfF
i ii
iii
O  
EA
RL
EA
RL
AE
LfF
i ii
iii
O   3
3
1
)3(
cos2

13. Example
13
 Calculate the forces in the members of the truss. All
members have the same cross-sectional area A and
Young’s modulus E.

14. Solution
14
 How many degrees of
redundancy are in the
structure?
 m=7
 r=5
 j=5
 NR=m+r-2j=2
6
1
2
34
5
7

15. Solution
15
2
1
4
R2
3
X1
X1

16. Solution
16
2 4
R2
3
X1
X1
0
0
)4()3()2(
)4()3()2(


CCC
ADADAD

17. Solution
17
2
F=10
00
0
-14.14
0
1
1
f=-0.71
0
-0.71
0-0.71
1
EAAE
LfF
i ii
ii
AD
1.276
1
)2( 
 

18. Solution
18
1
1
f=-0.71
0
-0.71
0-0.71
1
1
7
1
)3( 32.4
X
EAAE
LfF
i ii
ii
AD  
3
X1
X1
X1
X1
F=-0.71X1
0
-0.71X1
0-0.71X1
X1

19. Solution
19
1
1
f=-0.71
0
-0.71
0-0.71
1
2
6
1
)4( 7.2
R
EAAE
LfF
i ii
ii
AD  
4
R2
R2
F=-2R2
0
R2R2
1.41R2 -1.41R2

20. Solution
20
 Therefore our first linear equation becomes;
 Now we need another equation to solve two
unknowns X1 and R2
 This time we make sure vertical displacement at
node C becomes zero
 0)4()3()2(
ADADAD
07.232.41.27 21  RX

21. Solution
21
2
F=10
00
0
-14.14
0
f=-2
-1.410
11
1.41
EAAE
LfF
i ii
ii
C
11.486
1
)2( 
 

22. Solution
22
1
7
1
)3( 7.2
X
EAAE
LfF
i ii
ii
C  
3
X1
X1
X1
X1
F=-0.71X1
0
-0.71X1
0-0.71X1
X1
f=-2
-1.410
11
1.41

23. Solution
23
2
6
1
)4( 62.11
R
EAAE
LfF
i ii
ii
C  
R2
F=-2R2
-1.41R2
0
R2R2
1.41R2
4
R2
f=-2
-1.410
11
1.41

24. Solution
24
 Therefore our second linear equation becomes;
 Now by solving the two linear equations
simultaneously;
062.117.211.48 21  RX
 0)4()3()2(
CCC
062.117.211.48 21  RX
07.232.41.27 21  RX
kNRkNX 15.3,28.4 21 

25. Example
25
 Determine the reactions of the continuous beam in
the beam structure below, using force method.
L L
w
A B C

26. Solution
26
 Is the structure determinate or indeterminate?
w
 What is the degree of indeterminacy?
 3 equations (knowns)
A B C






0
0
0
z
y
x
M
F
F
 4 reactions (unknowns)

27. Solution
27
 I intentionally choose support at B as the redundant
 The released structure is then loaded by redundant
member
 Vertical displacement at B must be zero
w
A B C
RA RC
RB=XB
0B

28. Solution
28
 To determine redundant, we superimpose deflection due to
external load and a unit value of the redundant multiplied
by the magnitude of redundant XB
w
A C
A B
C
wL
wL
0B
10.5 0.5
BB

29. Solution
29
w
A C
w
A B
C
wL
wL
0B
10.5 0.5
BB
 00 BBBB X
    


EI
L
EI
Lw
BBB
48
21
,
384
25
34
0 
wLXR BB 25.1

30. Solution
30
w
A C
w
A B
C
wL
wL
0B
XB
1.25wL 1.25wL
BBBX 
  wLwLwLRA
8
3
25.15.0    wLwLwLRC
8
3
25.15.0 

31. Solution
31
w
A B C
(3/8)wL
(5/4)wL (3/8)wL
(3/8)wL
(5/8)wL
(-5/8)wL
(-3/8)wL
Shear

32. Solution
32
w
A B C
(3/8)wL
(5/4)wL (3/8)wL
(9/128)wL2
(-1/8)wL2
Moment
(9/128)wL2

33. Example
33
 How do you solve the following?

34. Solution
34

35. Example
35
 How about this one?

36. Solution
36

37. Example
37
 How about this one?

38. Solution
38
01221111  RRC
02222112  RRC

39. Q1
39
 Determine member forces and reaction at supports
of truss structure shown below. EA is constant for all
members.

40. Q2
40
 Determine forces in the truss structure shown below.
EA is constant for all members.

41. Q3
41
 A continuous beam ABC is carrying a uniformly
distributed load of 1 kN/m in addition to a
concentrated load of 10 kN. Draw bending moment
and shear force diagram. Assume EI to be constant
for all members.
A B C
1kN/m
10kN
10m5m5m

42. Q4
42
 The beam ABC shown in Figure is simply supported and stiffened by a
truss whose members are capable of resisting axial forces only. The
beam has a cross-sectional area of 6000mm2 and a second moment of
area of 7.2×106 mm4. If the cross-sectional area of the members of the
truss is 400mm2, calculate the forces in the members of the truss and
the maximum value of the bending moment in the beam. Young’s
modulus, E, is the same for all members.

43. Q5
43
 Draw the quantitative shear and moment diagram
and the qualitative deflected curve for the Frame
shown below. EI is constant.