This document contains lecture slides on first order logic inference from a course on artificial intelligence at the University of Hildesheim in Germany. It introduces concepts like unification, forward chaining, backward chaining and resolution. Forward chaining uses generalized modus ponens to iteratively infer new statements from a knowledge base consisting of Horn clauses. Backward chaining works in the opposite direction, trying to satisfy query atoms by matching them to rule heads and replacing with rule bodies.







![Artificial Intelligence / 2. Forward Chaining
Generalized Modus Ponens
premise conclusion name
F F, F F → G F G → -elimination / modus ponens
F F F Fθ universial instantiation
F F, F F → G, Fθ = F θ F Gθ generalized modus ponens
Lemma 1. Generalized modus ponens is sound.
Proof.
1. F F [assumption]
2. F Fθ [universal instantiation applied to 1]
3. F F → G [assumption]
4. F F θ → Gθ [universal instantiation applied to 3]
5. F Gθ [ → -elemination applied to 2,4]
Lars Schmidt-Thieme, Information Systems and Machine Learning Lab (ISMLL), University of Hildesheim, Germany,
Course on Artificial Intelligence, winter term 2012/2013 4/20](https://image.slidesharecdn.com/fol-180228095524/85/First-Order-Logic-8-320.jpg)







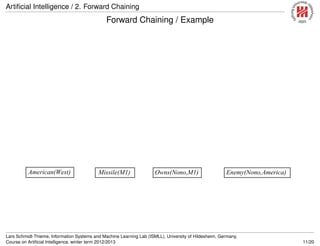
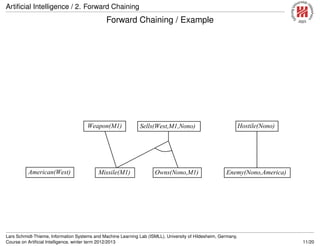
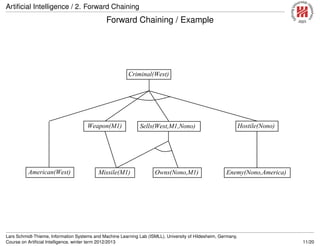


![Artificial Intelligence / 3. Backward Chaining
Backward Chaining / Algorithm
1 entails-bc(FOL definite horn formula F, query atom Q) :
2 return entails-bc-goals(clauses(F), {Q}, ∅) = ∅
3
4 entails-bc-goals(set of FOL definite Horn clauses C, set of FOL atoms Q, θ) :
5 if Q = ∅ return {θ} fi
6 Θ := ∅
7 for C ∈ C do
8 C′
:= standardize-apart(C)
9 θ′
:= unify(head(C′
), Q[1]θ)
10 if θ′
= failure
11 Θ := Θ ∪ entails-bc-goals(C, atoms(body(C′
)) ∪ (Q {C}), θ ∪ θ′
)
12 fi
13 od
14 return Θ
Lars Schmidt-Thieme, Information Systems and Machine Learning Lab (ISMLL), University of Hildesheim, Germany,
Course on Artificial Intelligence, winter term 2012/2013 13/20](https://image.slidesharecdn.com/fol-180228095524/85/First-Order-Logic-21-320.jpg)

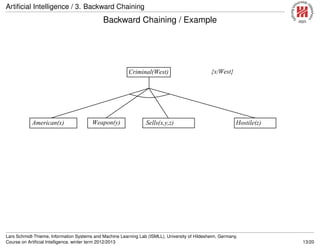
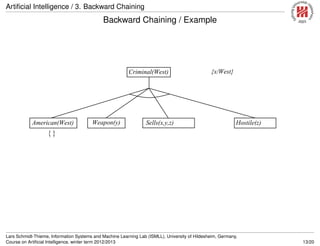
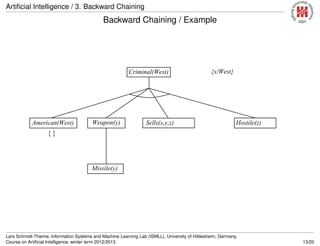
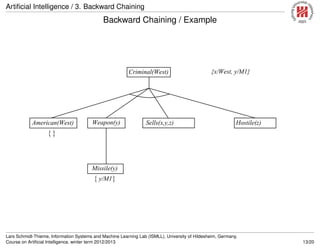
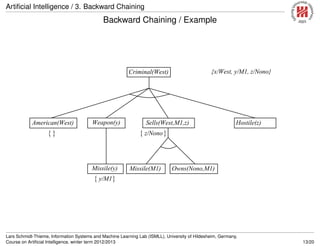
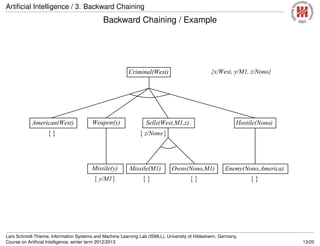


![Artificial Intelligence / 3. Backward Chaining
Prolog / Examples
Appending two lists to produce a third:
append(X,Y,Z) encodes that X appended to Y results in Z.
append([], Y, Y).
append([X|L], Y, [X|Z]) :- append(L, Y, Z).
query: append([1,2], [3,4], C) ?
answers: C=[1,2,3,4]
query: append(A, B, [1,2]) ?
answers: A=[] B=[1,2]
A=[1] B=[2]
A=[1,2] B=[]
Lars Schmidt-Thieme, Information Systems and Machine Learning Lab (ISMLL), University of Hildesheim, Germany,
Course on Artificial Intelligence, winter term 2012/2013 16/20](https://image.slidesharecdn.com/fol-180228095524/85/First-Order-Logic-31-320.jpg)


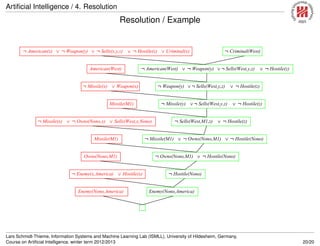
![Artificial Intelligence / 4. Resolution
Conversion to CNF
Everyone who loves all animals is loved by
someone:∀x[∀yAnimal(y) =⇒ Loves(x, y)] =⇒ [∃yLoves(y, x)]
1. Eliminate biconditionals and implications
∀x[¬∀y¬Animal(y) ∨ Loves(x, y)] ∨ [∃yLoves(y, x)]
2. Move ¬ inwards: ¬∀x, p ≡ ∃x¬p, ¬∃x, p ≡ ∀x¬p:
∀x[∃y¬(¬Animal(y) ∨ Loves(x, y))] ∨ [∃yLoves(y, x)]
∀x[∃y¬¬Animal(y) ∧ ¬Loves(x, y)] ∨ [∃yLoves(y, x)]
∀x[∃yAnimal(y) ∧ ¬Loves(x, y)] ∨ [∃yLoves(y, x)]
Lars Schmidt-Thieme, Information Systems and Machine Learning Lab (ISMLL), University of Hildesheim, Germany,
Course on Artificial Intelligence, winter term 2012/2013 18/20](https://image.slidesharecdn.com/fol-180228095524/85/First-Order-Logic-34-320.jpg)
![Artificial Intelligence / 4. Resolution
Conversion to CNF
3. Standardize variables: each quantifier should use a different
one
∀x[∃yAnimal(y) ∧ ¬Loves(x, y)] ∨ [∃zLoves(z, x)]
4. Skolemize: a more general form of existential instantiation.
Each existential variable is replaced by a Skolem function
of the enclosing universally quantified variables:
∀x[Animal(F(x)) ∧ ¬Loves(x, F(x))] ∨ Loves(G(x), x)
5. Drop universal quantifiers:
[Animal(F(x)) ∧ ¬Loves(x, F(x))] ∨ Loves(G(x), x)
6. Distribute ∧ over ∨:
[Animal(F(x))∨Loves(G(x), x)]∧[¬Loves(x, F(x))∨Loves(G(x), x)]
Lars Schmidt-Thieme, Information Systems and Machine Learning Lab (ISMLL), University of Hildesheim, Germany,
Course on Artificial Intelligence, winter term 2012/2013 19/20](https://image.slidesharecdn.com/fol-180228095524/85/First-Order-Logic-35-320.jpg)