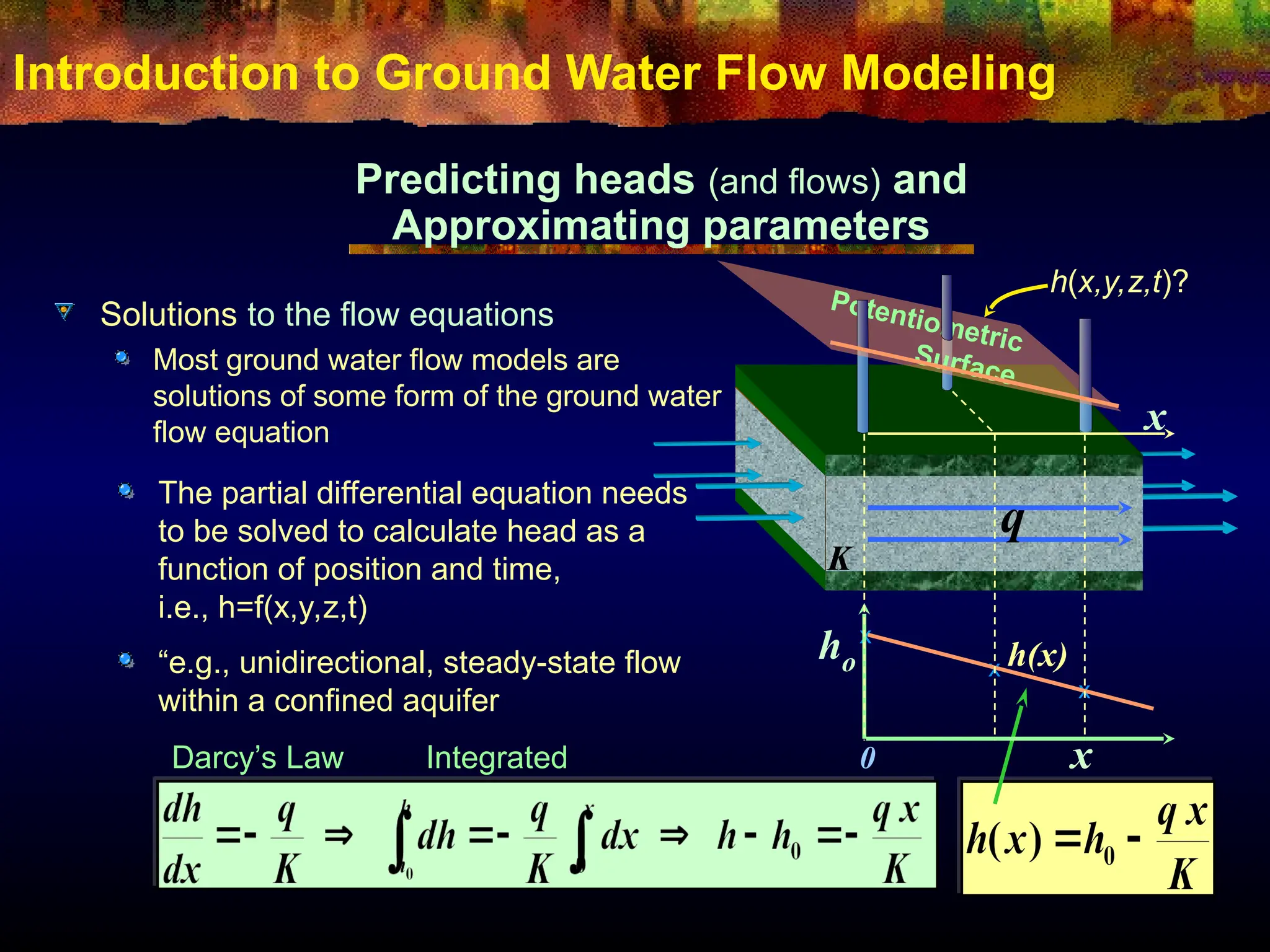
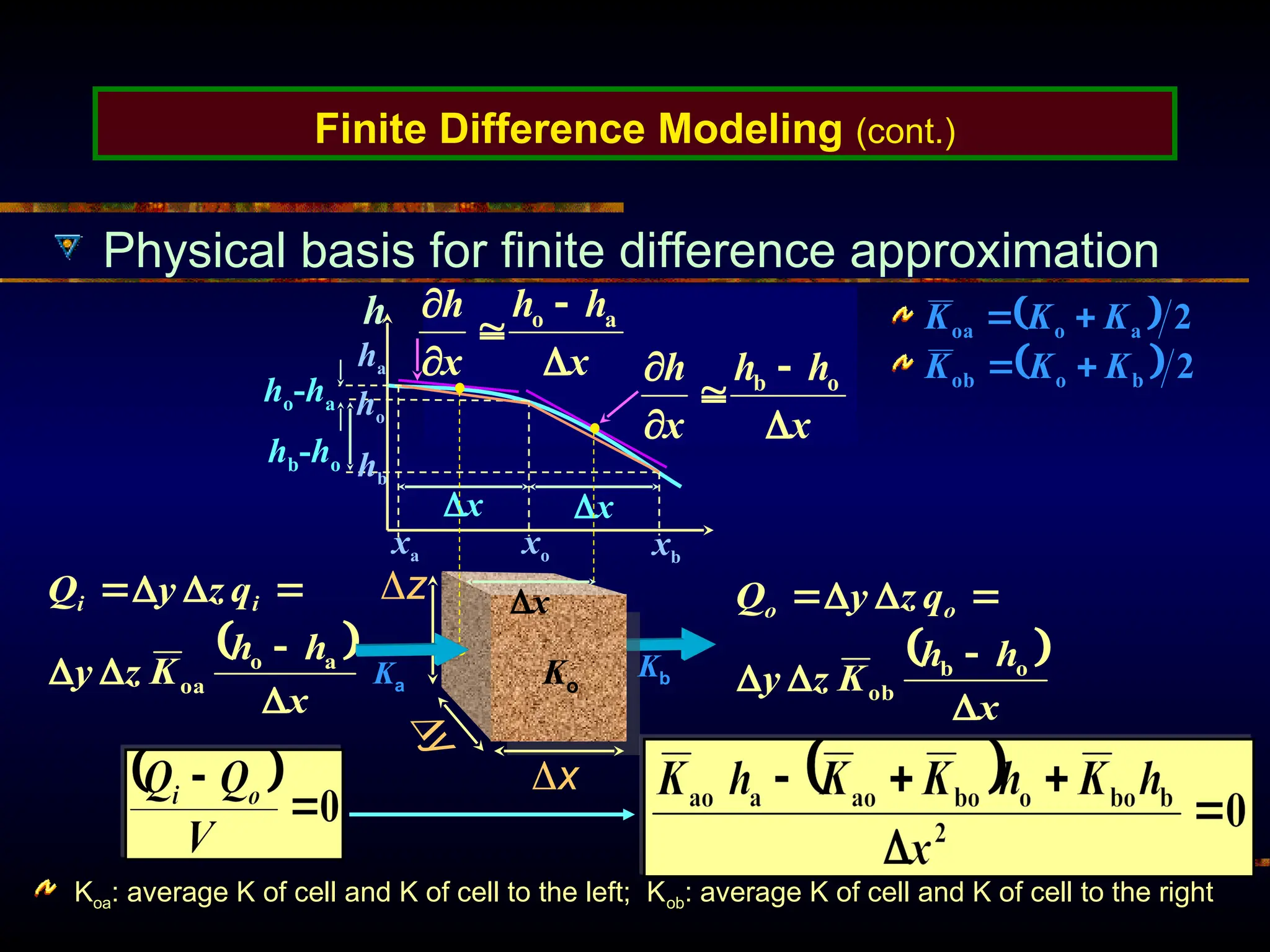
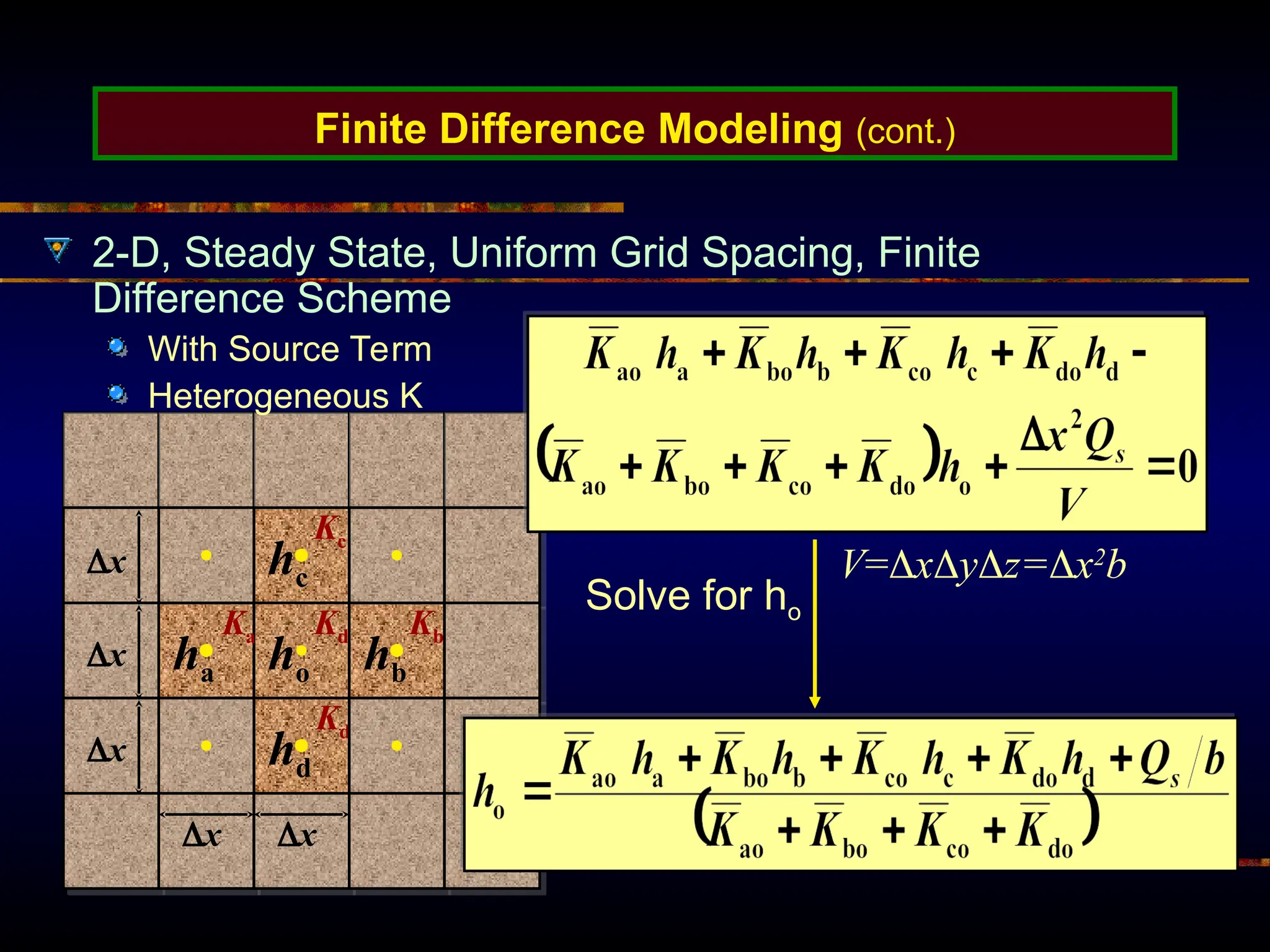
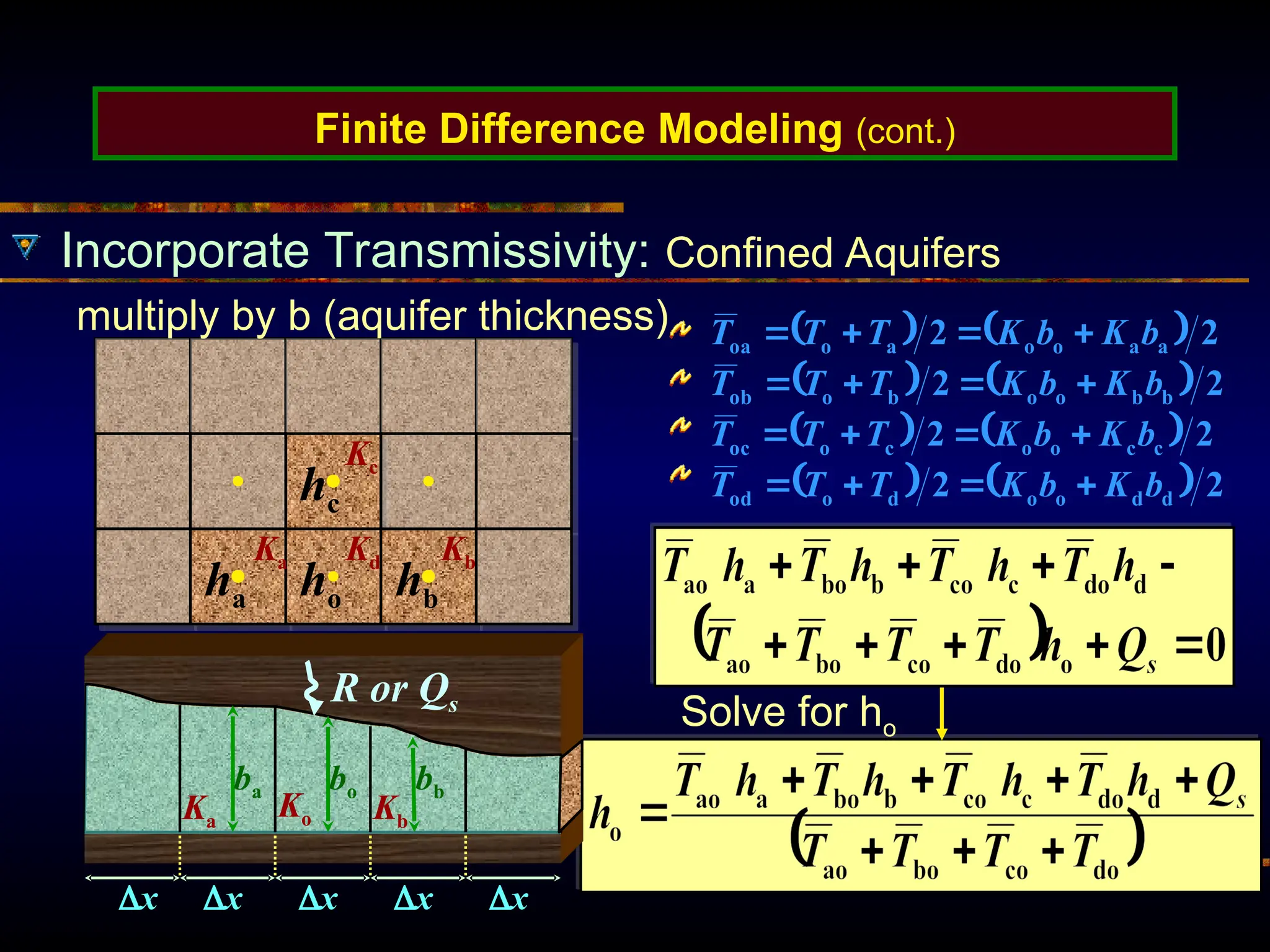
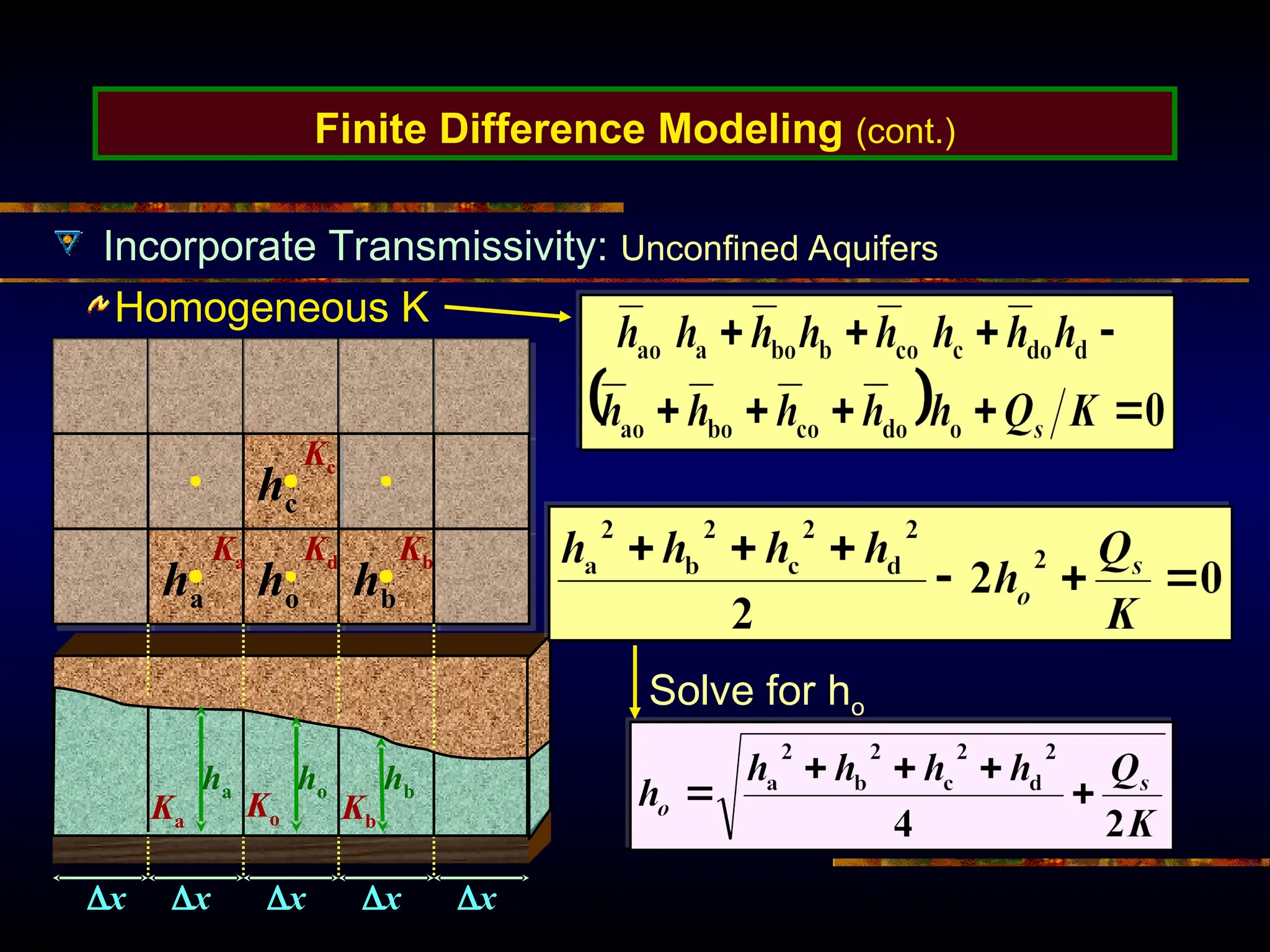
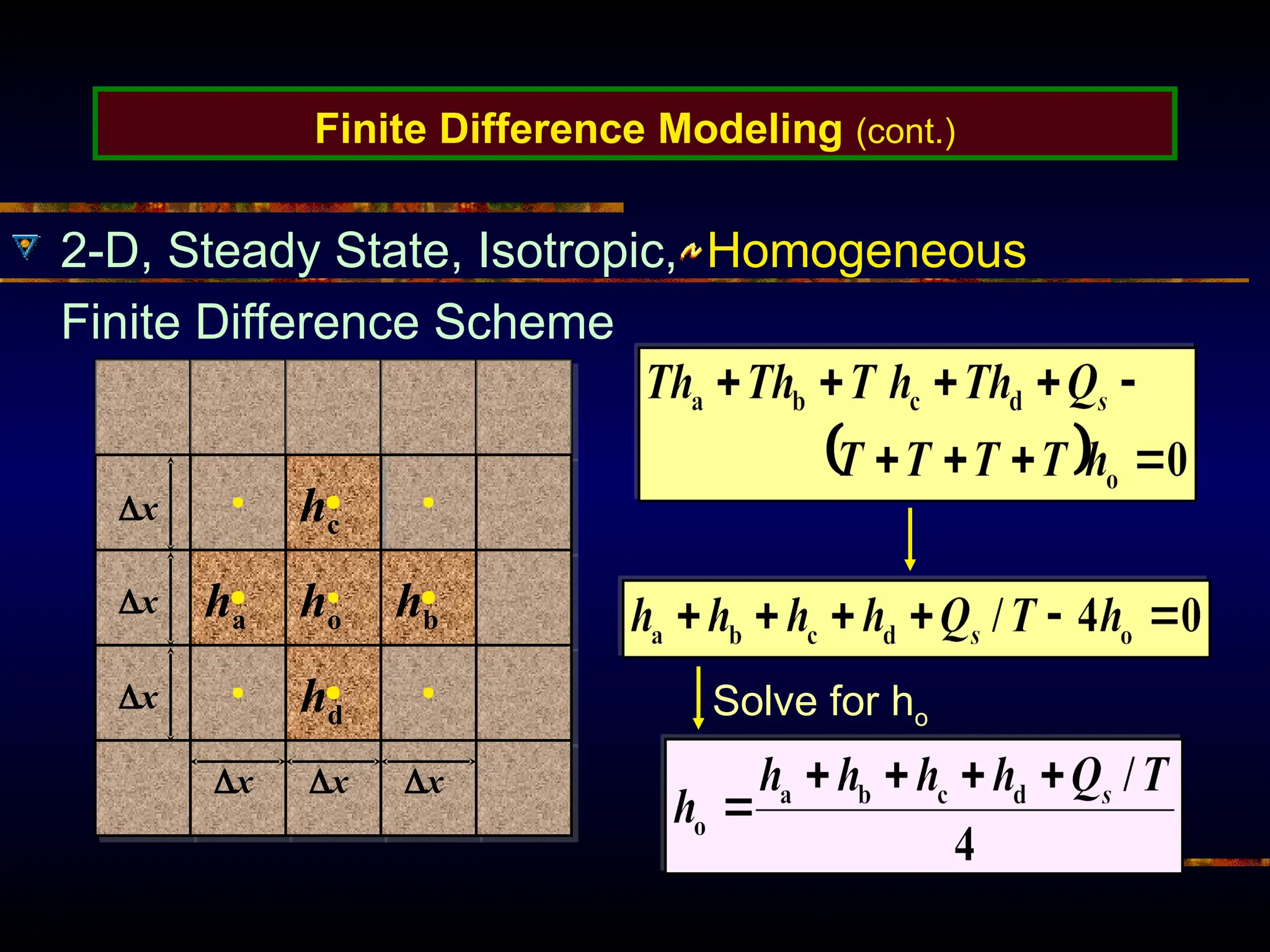
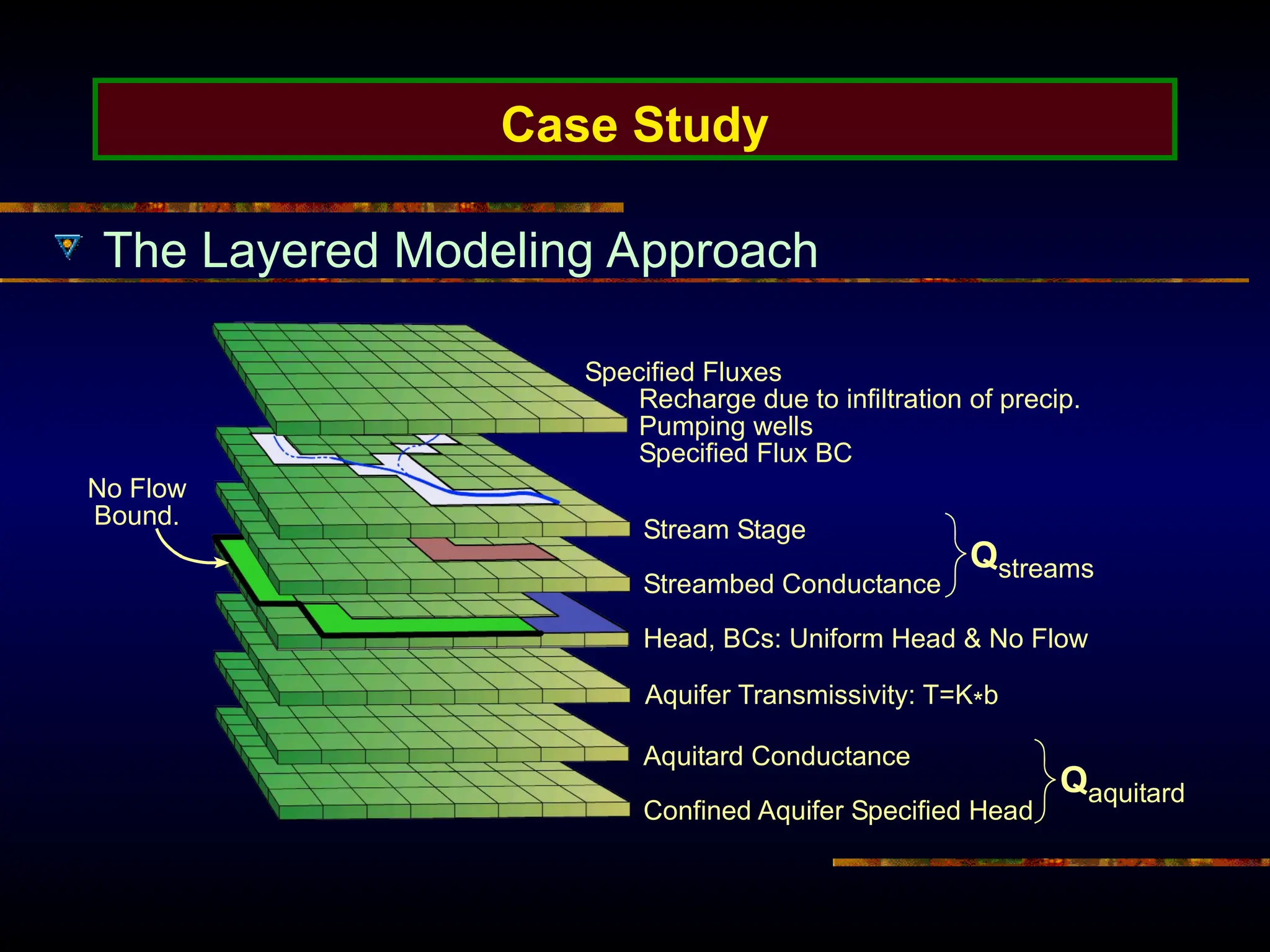
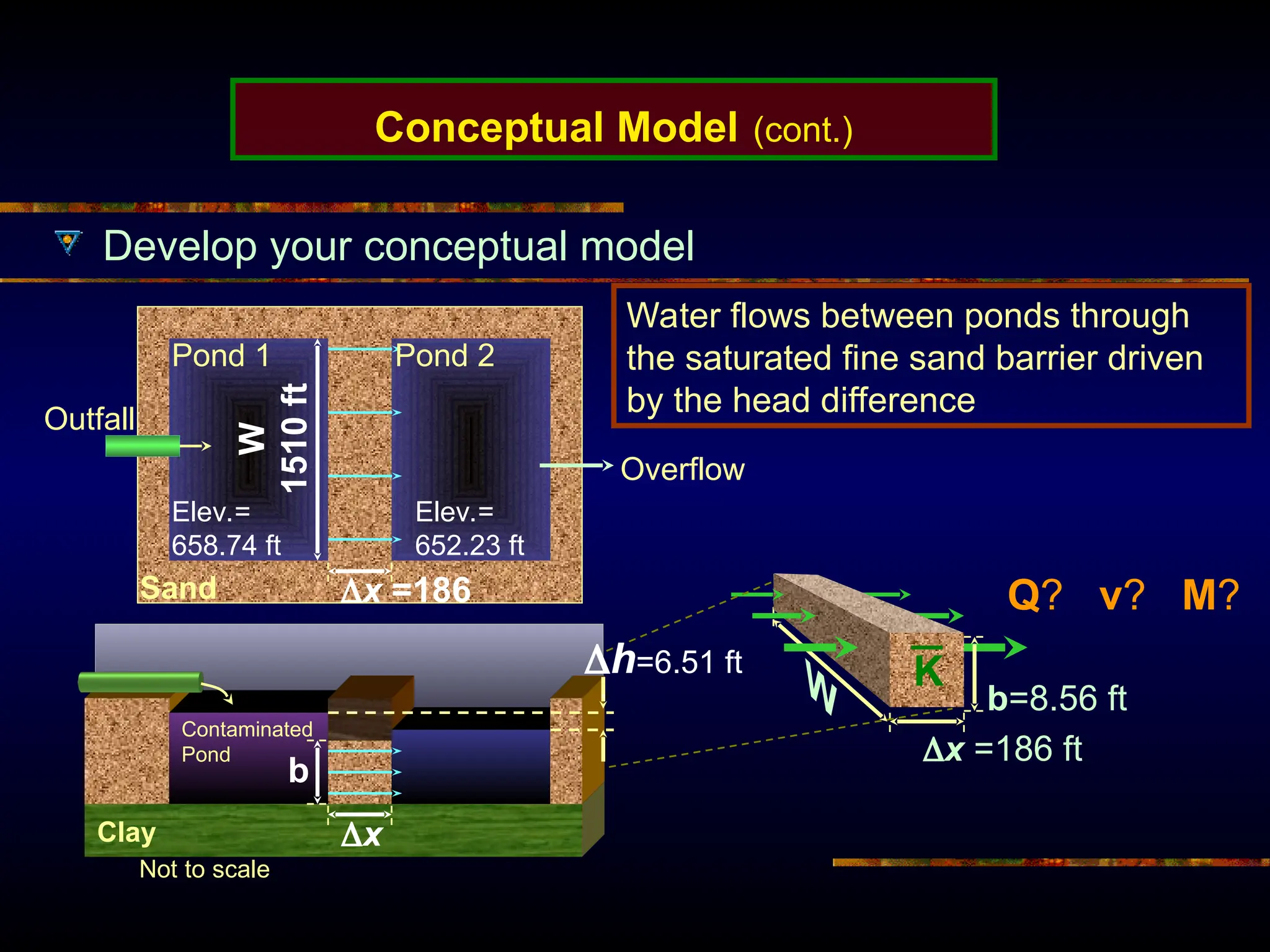
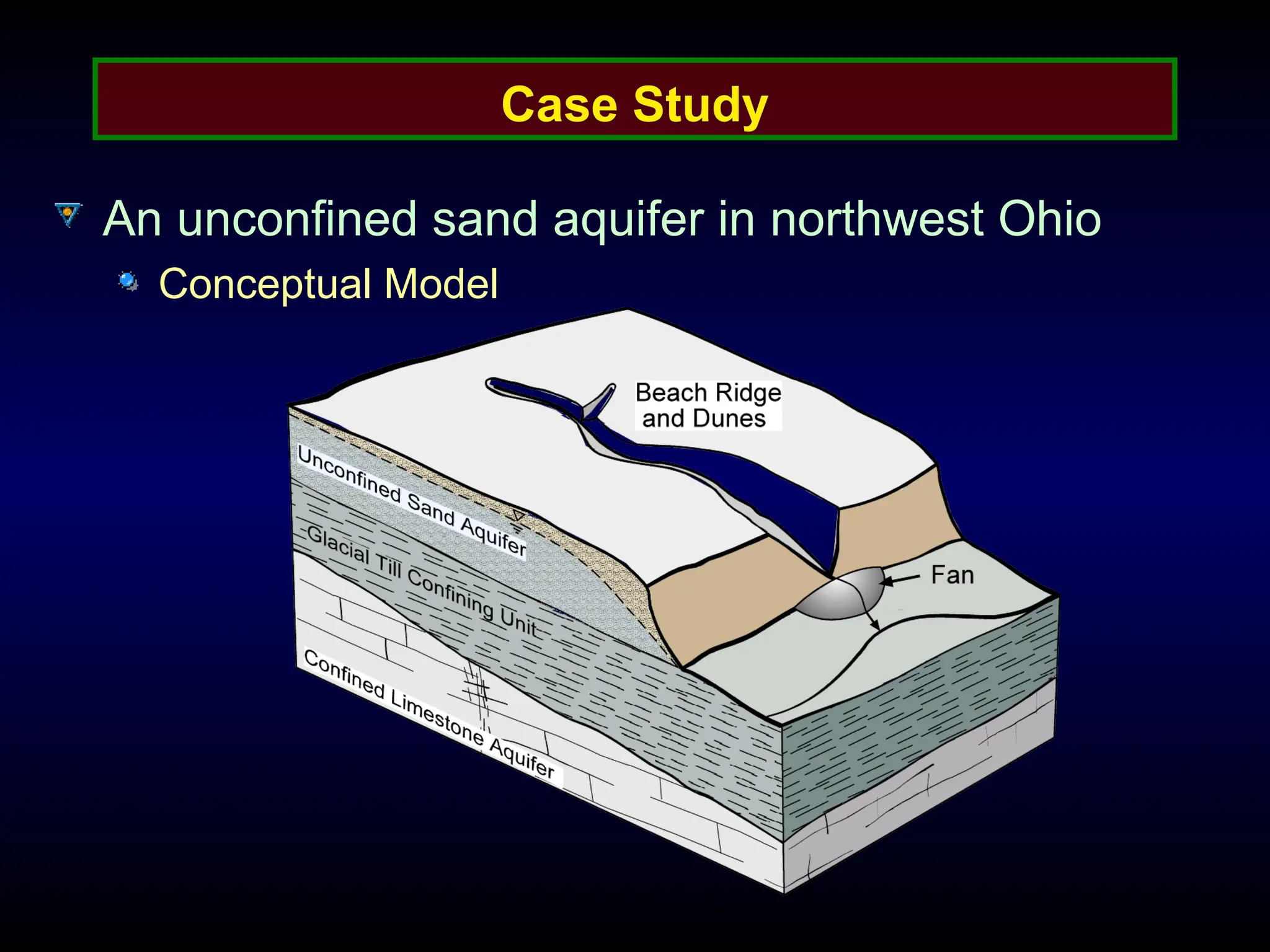
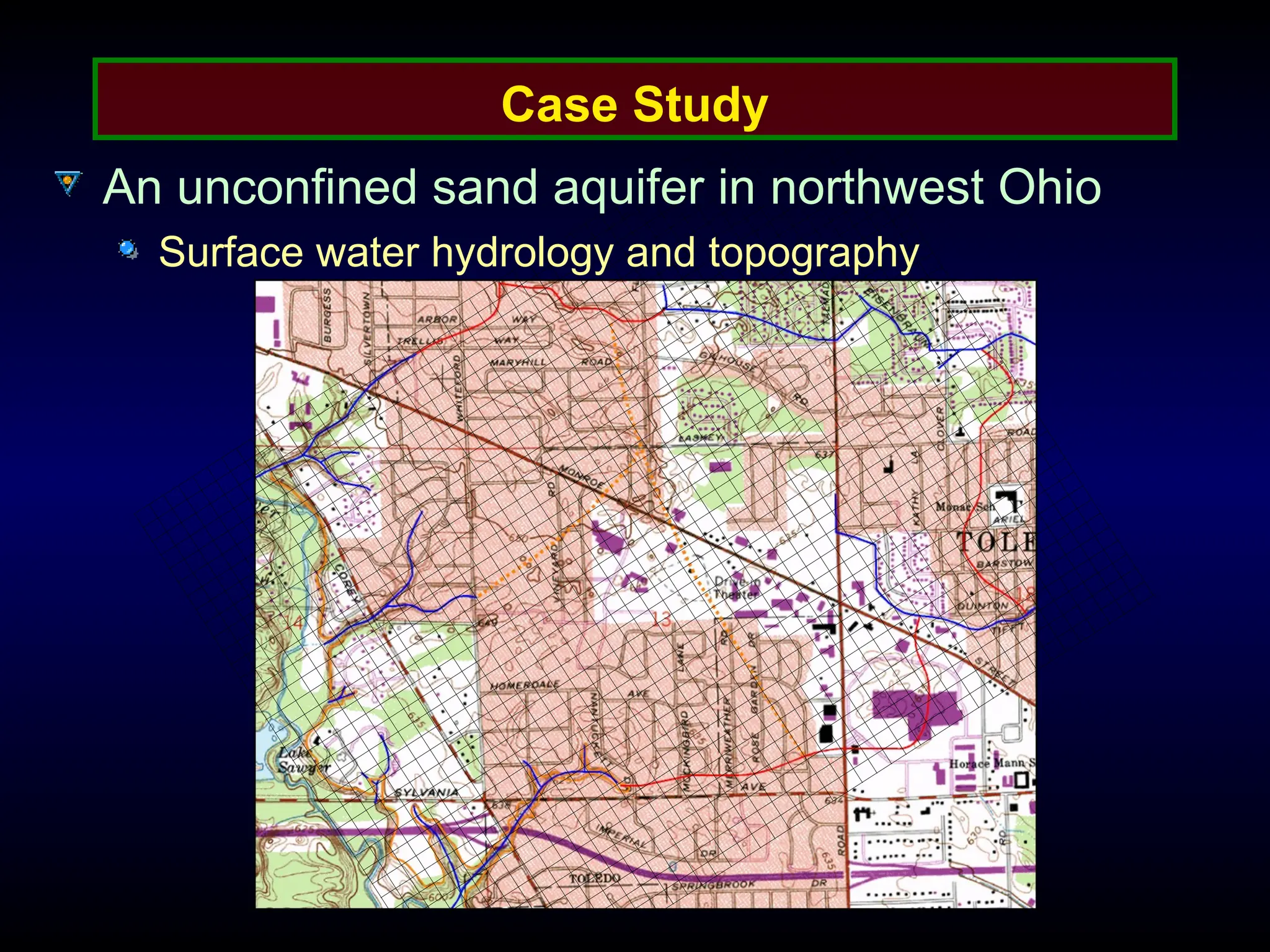
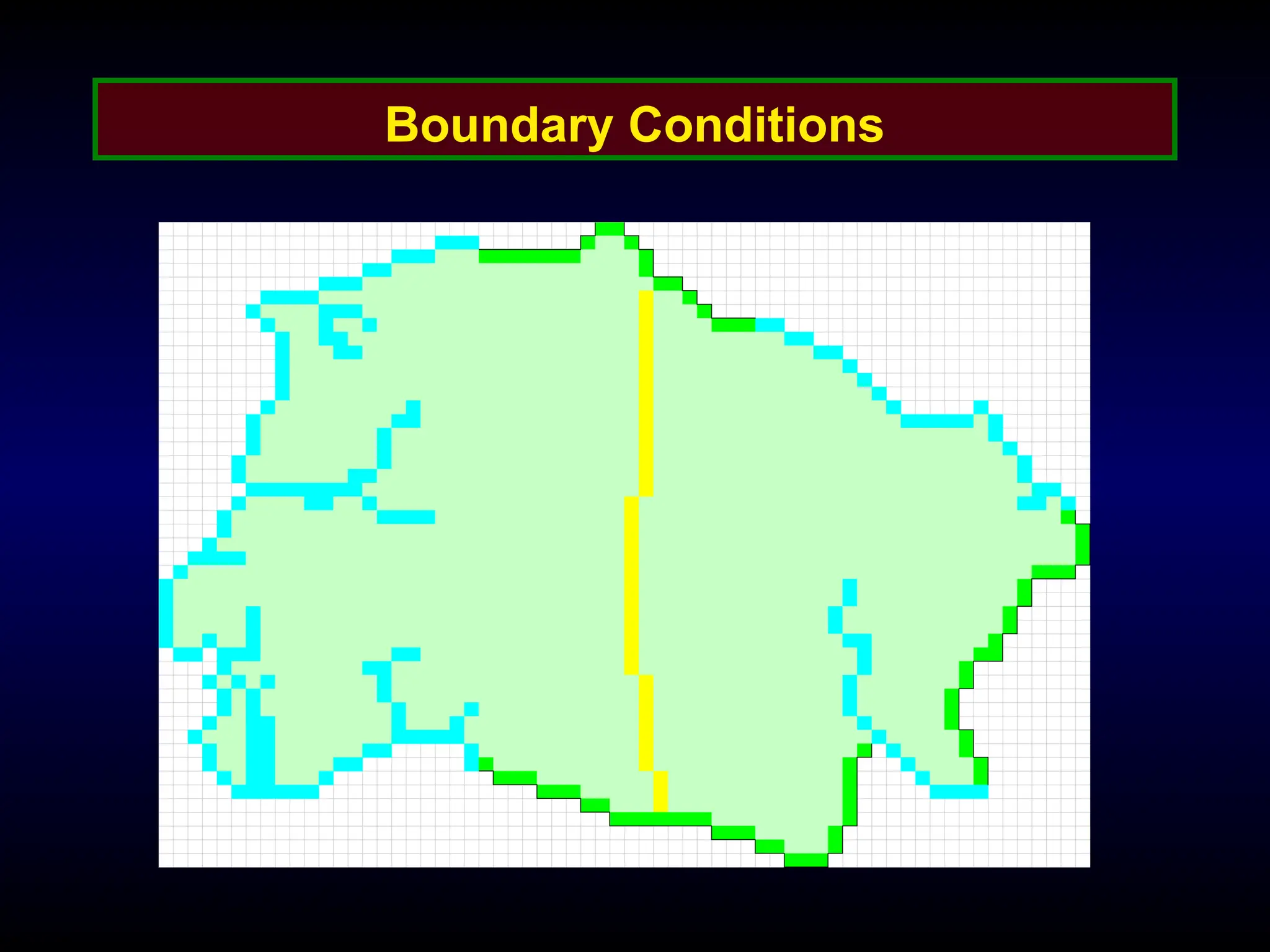
The document provides an introduction to ground water flow modeling, emphasizing the importance of the mass balance equation and the flow equation in modeling strategies. It discusses analytical and numerical methods for solving flow equations, including forward and inverse modeling, as well as the use of finite difference methods for approximating solutions. The limitations of analytical models and the need for more complex numerical modeling to address geological complexities are also highlighted.

1. Dr. James M. Martin-Hayden
Associate Professor
Analytical and Numerical
Ground Water Flow Modeling
An Introduction
(419) 530-2634
Jhayden@Geology.UToledo.edu

2. The Ground Water Flow Equation
Mass Balance Objective of modeling: represent h=f(x,y,z,t)
A common method of analysis in sciences
For a “system”, during a period of time (e.g., a unit of time),
Assumption: Water is incompressible
Mass per unit volume (density, ) does not change significantly
Volume is directly related to mass by density V=m/
In this case water balance models are essentially mass balance
models divided by density
Mass In – Mass Out = Change in Mass Stored
Volume In – Volume Out = Change in Volume Stored
Qi – Qo = Vw /t
Dividing by
unit time gives:
If Q is a continuous function of time Q(t) then dv/dt is at any instant in time
Qi(t) – Qo(t) = dVw/dt

3. The Flow Equation (cont.)
Example 1: Storage in a reservoir
If Qi = Qo, dVw/dt = 0  no change in level, i.e., steady state
If Qi > Qo, dVw/dt > 0 +filling If Qi < Qo, dVw/dt < 0  -emptying
E.g., Change in storage due to
linearly varying flows
Qi Qo
dVw/dt
Qi(t) – Qo(t) = dVw/dt
Q1
Q2
Qi =m
1·t+Q1 Qo
=m2
·t+Q2
t
Q
0
dV/dt = 0
dV/dt < 0
dV/dt > 0

4. The Flow Equation (cont.)
Example 1: Storage in a reservoir
If Qi = Qo, dVw/dt = 0  no change in level, i.e., steady state
If Qi > Qo, dVw/dt > 0 +filling If Qi < Qo, dVw/dt < 0  -emptying
Qi Qo
dVw/dt
Qi(t) – Qo(t) = dVw/dt
Q1
Q2
Qi =m
1·t+Q1 Qo
=m2
·t+Q2
t
Q
0
dV/dt = 0
dV/dt < 0
dV/dt > 0
t
V
dV/dt = 0
dV/dt < 0
dV/dt > 0

5. The Flow Equation (cont.)
Example 1: Storage in a reservoir
If Qi = Qo, dVw/dt = 0  no change in level, i.e., steady state
If Qi > Qo, dVw/dt > 0 +filling If Qi < Qo, dVw/dt < 0  -emptying
Example 2: Storage in a REV (Representative Elementary Volume)
REV: The smallest parcel of a unit that has
properties (n, K, …) that are representative
of the formation
The same water balance can be used to examine the saturated (or
unsaturated) REV
Qi
Qo
dVw/dt
Qi(t) – Qo(t) = dVw/dt

6. Qo = qo y z
The Flow Equation (cont.)
Mass Balance for the REV (or any volume of a flow system)
aka, “The Ground Water Flow Equation”
x

y
z
Vw/t
Qi – Qo = dVw/dt
y z x = V
(qi– qo)yz =dVw/dt
Qi – Qo =
(qo – qi)= q= (q/x) x
Take change in q with x at a point
(the derivative of q rwt x)
For saturated,
incompressible,
1-D flow
n
V
Vw 
Qi=qi y z

7. The Flow Equation (cont.)
External Sources and Sinks (Qs)
y z x = V
Differential
Form

8. The Flow Equation (cont.)
3-D, flow equation
Summing the mass balance equation for each coordinate direction
gives the total net inflow per unit volume into the REV
Add a source term Qs/V volumetric flow rate per unit volume injected
into REV
Net inflow* =
Change in
volume stored*
*per unit volume per unit time
qx
qz
qy
Substitute components of q from 3-D Darcy’s law

9. The Flow Equation (cont.)
Specific storage and homogeneity
Due to aquifer compressibility: change in porosity is proportional
to a change in head (over a infinitesimally small range, dh)*
Assumption: K is homogeneous over small distances, i.e., K  f(x,y,z)
Compressibility of water is much less than aquifer compressibility
This gives the equation on which ground water flow
models are based: h=f(x,y,z,t)
Ss: Specific Storage, a proportionality constant

10. The Flow Equation (cont.)
Flow Equation Simplifications
0
Our job is not yet finished, h=f(x,y,z,t)?
Isotropic, 2-D, steady state flow equation
(without source term), a.k.a.: The Laplace Equation
2-D, horizontally isotropic flow equation
Kx=Ky=Kh
T=Kh b units: [L2
/T], S=Ss b
Ah: horizontal area of recharge
Ss/Kh=S/T  hydraulic diffusivity
Two dimensional flow equation
Horizontal flow (Dupuit assumption)
Thus: dh/dz = 0
Steady State Flow Equation
If inflow = out flow, Net inflow = 0
Change in storage = 0
0
0 0

11. Introduction to Ground Water Flow Modeling
Predicting heads (and flows) and
Approximating parameters
Solutions to the flow equations
Most ground water flow models are
solutions of some form of the ground water
flow equation
Potentiometric
Surface
x
x
x
ho
x
0
h(x)
x
K
q
“e.g., unidirectional, steady-state flow
within a confined aquifer
The partial differential equation needs
to be solved to calculate head as a
function of position and time,
i.e., h=f(x,y,z,t)
h(x,y,z,t)?
Darcy’s Law Integrated

12. Flow Modeling (cont.)
Analytical models (a.k.a., closed form models)
The previous model is an example of an analytical model
is a solution to the
1-D Laplace equation
i.e., the second derivative
of h(x) is zero
With this analytical model, head can be calculated at any position (x)
Analytical solutions to the 3-D transient flow equation would give head at any
position and at any time, i.e., the continuous function h(x,y,z,t)
Examples of analytical models:
1-D solutions to steady state and transient flow equations
Thiem Equation: Steady state flow to a well in a confined aquifer
The Theis Equation: Transient flow to a well in a confined aquifer
Slug test solutions: Transient response of head within a well to a
pressure pulse

13. Flow Modeling (cont.)
Common Analytical Models
Thiem Equation: steady state flow to a well within a confined aquifer
Analytic solution to the radial (1-D), steady-state, homogeneous K
flow equation
Gives head as a function of radial distance
Theis Equation: Transient flow to a well within a confined aquifer
Analytic solution of radial, transient, homogeneous K flow equation
Gives head as a function of radial distance and time

14. Pump Tests an Groundwater Modeling
h as a function of r (radial distance) and t (time)
Aquitard
Aquifer
Aquitard
r1 r2
h1
h2
Q
T?, S?

15. Flow Modeling (cont.)
Forward Modeling: Prediction
Models can be used to predict h(x,y,z,t) if the parameters are known, K,
T, Ss, S, n, b…
Heads are used to predict flow rates,velocity distributions, flow paths,
travel times. For example:
Velocities for average contaminant transport
Capture zones for ground water contaminant plume capture
Travel time zones for wellhead protection
Velocity distributions and flow paths are then used in contaminant
transport modeling
1-D, SS Thiem Theis

16. Flow Modeling (cont.)
Inverse Modeling: Aquifer Characterization
Use of forward modeling requires estimates of aquifer
parameters
Simple models can be solved for these parameters
e.g., 1-D Steady State:
This inverse model can be used to “characterize” K
This estimate of K can then be used in a forward model to
predict what will happen when other variables are changed
ho
h1
Clay
b
x
ho h1
Q Q

17. Flow Modeling (cont.)
Inverse Modeling: Aquifer Characterization
The Thiem Equation can also be solved for K
Pump Test: This inverse model allows measurement of K
using a steady state pump test
A pumping well is pumped at a constant rate of Q until heads
come to steady state, i.e.,
The steady-state heads, h1 and h2, are measured in two
observation wells at different radial distances from the
pumping well r1 and r2
The values are “plugged into” the inverse model to calculate
K (a bulk measure of K over the area stressed by pumping)
)
(t
f
h 

18. Flow Modeling (cont.)
Inverse Modeling: Aquifer Characterization
Indirect solution of flow models
More complex analytical flow models cannot be solved for the
parameters
Curve Matching
or Iteration
This calls for curve matching or iteration in order to calculate the
aquifer parameters
Advantages over steady state solution
gives storage parameters S (or Ss) as well as T (or K)
Pump test does not have to be continued to steady state
Modifications allow the calculation of many other parameters
e.g., Specific yield, aquitard leakage, anisotropy…

19. Flow Modeling (cont.)
Limitations of Analytical Models
Closed form models are well suited to the
characterization of bulk parameters
However, the flexibility of forward modeling
is limited due to simplifying assumptions:
Homogeneity, Isotropy, simple geometry,
simple initial conditions…
Geology is inherently complex:
Heterogeneous, anisotropic, complex
geometry, complex conditions…
This complexity calls for a more
powerful solution to the flow equation  Numerical modeling

20. Numerical Modeling in a Nutshell
A solution of flow equation is approximated on a
discrete grid (or mesh) of points, cells or elements
Within this discretized domain:
1)Aquifer parameters can be set at each cell
within the grid
2)Complex aquifer geometry can be modeled
3)Complex boundary conditions can be
accounted for
Requires detailed knowledge of 1), 2) , and 3)
As compared to analytical modeling, numerical
modeling is:
Well suited to prediction but
More difficult to use for aquifer characterization
Flow Modeling (cont.)
The parameters and variables are specified over the
boundary of the domain (region) being modeled

21. An Introduction to Finite Difference Modeling
Approximate Solutions to the
Flow Equation
Partial derivatives of head represent the
change in head with respect to a
coordinate direction (or time) at a point.e.g., t
h
or
y
h 



h
y
h
y
h1
h2
y1 y2
y
h
y
h





These derivatives can be approximated as
the change in head (h) over a finite
distance in the coordinate direction (y)
that traverses the point
i.e., The component of the hydraulic
gradient in the y direction can be
approximated by the finite difference h/y
The Finite Difference Approximation of Derivatives

22. Finite Difference Modeling (cont.)
Approximation of the second derivative
The second derivative of head with respect to x represents the change
of the first derivative with respect to x
The second derivative can be approximated using two finite differences
centered around x2
This is known as a central difference
h
x
x
ha
ho
xo xb
xa
x
hb
ho-ha
hb-ho
x
x
h
h
y
h




 a
o
x
h
h
y
h




 o
b

23. Finite Difference Modeling (cont.)
Finite Difference Approximation of
1-D, Steady State Flow Equation
 
1-D, Steady State Flow Equation
With external source (Qs)
 
Qs/Ah = R

24. Finite Difference Modeling (cont.)
Physical basis for finite difference approximation
h
x
ha
ho
xo xb
xa
x
hb
ho-ha
hb-ho
x
x
h
h
x
h




 a
o
x
h
h
x
h




 o
b
 
x
h
h
K
z
y
q
z
y
Q i
i








a
o
oa
 
x
h
h
K
z
y
q
z
y
Q o
o








o
b
ob
Koa: average K of cell and K of cell to the left; Kob: average K of cell and K of cell to the right
 
  2
2
b
o
ob
a
o
oa
K
K
K
K
K
K





y
z
x
Ka
Kb
Ko

25. Finite Difference Modeling (cont.)
Inclusion of and external
source
Koa: average K of cell and K of cell to the left; Kob: average K of cell and K of cell to the right

y
z
x
Ka
Kb
Ko
Qs
Qi
Qo

26. Finite Difference Modeling (cont.)
Discretization of the Domain
Divide the 1-D domain into equal cells
of heterogeneous K
… …
h1 h2 h3 hi-1 hn
x x x x x x x
 
 
head
specified
:
and
Constant
2
2
1
n
o
1
i
i
1/2
i
1
-
i
i
1/2
-
i









h
h
x
K
K
K
K
K
K
    
…
hi hi+1
x x
 
Solve for the head at each node gives n
equations and n unknowns
The head at each node is an average of
the head at adjacent cells weighted by
the Ks
ho hn+1
Specified
Head
Specified
Head

27. Finite Difference Modeling (cont.)
2-D, Steady State, Uniform Grid Spacing, Finite
Difference Scheme
Divide the 2-D domain into equally
spaced rows and columns of
heterogeneous K
ha ho hb
hd
hc
x
x
x
 
 
 
  2
2
2
2
d
o
od
c
o
oc
b
o
ob
a
o
oa
K
K
K
K
K
K
K
K
K
K
K
K








Ka
Kc
Kb
Kd
Kd
x x x
Solve for ho

28. Finite Difference Modeling (cont.)
2-D, Steady State, Uniform Grid Spacing, Finite
Difference Scheme
With Source Term
Heterogeneous K
ha ho hb
hd
hc
x
x
x
Ka
Kc
Kb
Kd
Kd
x x
Solve for ho
V=xyz=x2
b

29. ha ho hb
hc
Ka
Kc
Kb
Kd
Finite Difference Modeling (cont.)
Incorporate Transmissivity: Confined Aquifers
multiply by b (aquifer thickness)    
   
   
    2
2
2
2
2
2
2
2
d
d
o
o
d
o
od
c
c
o
o
c
o
oc
b
b
o
o
b
o
ob
a
a
o
o
a
o
oa
b
K
b
K
T
T
T
b
K
b
K
T
T
T
b
K
b
K
T
T
T
b
K
b
K
T
T
T
















x x x x x
Ko Kb
Ka
ba bo bb
Solve for ho
R or Qs

30. ha ho hb
hc
Ka
Kc
Kb
Kd
x x x x x
Ko Kb
Ka
ha ho hb
Finite Difference Modeling (cont.)
Incorporate Transmissivity: Unconfined Aquifers
b depends on saturated thickness which is head (h)
measured relative to the aquifer bottom  
 
 
  2
2
2
2
d
o
od
c
o
oc
b
o
ob
a
o
oa
h
h
h
h
h
h
h
h
h
h
h
h








Solve for ho

31. ha ho hb
hc
Ka
Kc
Kb
Kd
x x x x x
Ko Kb
Ka
ha ho hb
Finite Difference Modeling (cont.)
Incorporate Transmissivity: Unconfined Aquifers
Homogeneous K
Solve for ho

32. Finite Difference Modeling (cont.)
2-D, Steady State, Isotropic, Homogeneous
Finite Difference Scheme
ha ho hb
hd
hc
x
x
x
x x x
Solve for ho

33. Finite Difference Modeling (cont.)
Spreadsheet Implementation
Spreadsheets provide all you need to do basic finite
difference modeling
Interdependent calculations among grids of cells
Iteration control
Multiple sheets for multiple layers, 3-D, or heterogeneous
parameter input
Built in graphics: x-y scatter plots and basic surface plots
A B C D E…
1
2
3
4
…

34. Finite Difference Modeling (cont.)
Spreadsheet Implementation of
2-D, Steady State, Isotropic,
Homogeneous Finite Difference
Type the formula into a
computational cell
Copy that cell into all other interior
computational cell and the references
will automatically adjust to calculate
value for that cell
Note: Boundary cells will be treated
differently
hB3 hC3 hD3
hC4
hC2
A B C D E…
1
2
3
4
5
= (C2+D3+C4+B3)/4

35. Finite Difference Modeling (cont.)
A simple example
This will give a circular
reference error
Set Tools:Options…
Calculation to Manual
Select Tools:Options…
Itteration
SetMaximum Iteration
and Maximum Change
Press F9 to iteratively
calculate
10
A B C D E…
2
3
4
5
10 10
10
10
10
7 5 2
1
1
1
Lake 1
Lake
2
River

36. Basic Finite Difference Design
Discretization and
Boundary Conditions
Grids should be oriented and spaced to
maximize the efficiency of the model
Boundary conditions should represent
reality as closely as possible

37. Basic Finite Difference Design (cont.)
Discretization: Grid orientation
Grid rows and columns should line up with as many rivers,
shorelines, valley walls and other major boundaries as much
as possible

38. Basic Finite Difference Design (cont.)
Discretization: Variable Grid Spacing
Rules of Thumb
Refine grid around areas
of interest
Adjacent rows or columns
should be no more than
twice (or less than half)
as wide as each other
Expand spacing smoothly
Many implementations of
Numerical models allow
Onscreen manipulation of
Grids relative to an imported
Base map

39. Basic Finite Difference Design (cont.)
Boundary Conditions
Any numerical model must be bounded on all sides of
the domain (including bottom and top)
The types of boundaries and mathematical
representation depends on your conceptual model
Types of Boundary Conditions
Specified Head Boundaries
Specified Flux Boundaries
Head Dependant Flux Boundaries

40. Basic Finite Difference Design (cont.)
Specified Head Boundaries
Boundaries along which the heads have been
measured and can be specified in the model
e.g., surface water bodies
They must be in good hydraulic connection
with the aquifer
Must influence heads throughout layer being modeled
Large streams and lakes in unconfined aquifers
with highly permeable beds
Uniform Head Boundaries: Head is uniform in space,
e.g., Lakes
Spatially Varying Head Boundaries: e.g., River
heads can be picked of of a topo map if:
Hydraulic connection with and unconfined aquifer
the streambed materials are more permeable than
the aquifer materials

41. Basic Finite Difference Design (cont.)
Specified Flux Boundaries
Boundaries along which, or cells
within which, inflows or outflows
are set
Recharge due to infiltration (R)
Pumping wells (Qp)
Induced infiltration
Underflow
No flow boundaries
Valley wall of low permeable
sediment or rock
Fault

42. Finite Difference Modeling (cont.)
No Flow Boundary Implementation
A special type of specified flux boundary
Because there are no nodes outside the domain,
the perpendicular node is reflected across the
boundary as and “image node”
hB3
hC4
hA2
A B
C
D E…
1
2
4
5
= (A2 +2*B3 +C4)/4
= (B1+D1+2*C2)/4
A3
C1
E3 = (2*D3+E2 +E4)/4
= (B5+2*C4+D5)/4
C5
hA3
hB3

43. Finite Difference Modeling (cont.)
No Flow Boundary Implementation
Corner nodes have two image nodes
B C D E…
2
4
5
= (2*B1 +2*A2)/4
= (2*D1+2*E2)/4
A1
E1
E5 = (2*D5+2*E4)/4
= (2*A4+2*B5)/4
A5
3

44. Finite Difference Modeling (cont.)
No Flow Boundary Implementation
Combinations of edge and corner points are used
to approximate irregular boundaries

45. Finite Difference Modeling (cont.)
Head Dependent Flux Boundaries
Flow into or out of cell depends on the difference
between the head in the cell and the head on the
other side of a conductive boundary
e.g. 1, Streambed conductance
hs: stage of the stream
ho: Head within the cell
Ksb: K of streambed materials
bsb: Thickness of streambed
w: width of stream
L: length of reach within cell
Csb: Streambed conductance
Based on Darcys law
1-D Flow through streambed
hs
ho
w
L
bsb
Qsb
Qsb

46. Finite Difference Modeling (cont.)
Head Dependent Flux Boundaries
e.g. 2, Flow through aquitard
hc: Head within confined aquifer
Ho: Head within the cell
Kc: K of aquitard
bc: Thickness of aquitard
x2
: Area of cell
Cc: aquitard conductance
Based on Darcys law
1-D Flow through aquitard
ho
hc
x
bc
Qc
Qc
x

47. Case Study
The Layered Modeling Approach
Head, BCs: Uniform Head & No Flow
Streambed Conductance
Stream Stage
Aquitard Conductance
Confined Aquifer Specified Head
Qstreams
Qaquitard
Aquifer Transmissivity: T=K*b
Specified Fluxes
Recharge due to infiltration of precip.
Pumping wells
Specified Flux BC
No Flow
Bound.

48. Finite Difference Modeling (cont.)
3-D Finite Difference Models
Approximate solution to the 3-D flow equation
e.g., 3-D, Steady State, Homogeneous Finite
Difference approximation
3-D Computational Cell
ha ho hb
hd
hc
hf

49. Finite Difference Modeling (cont.)
3-D Finite Difference Models
Requires vertical discretization (or layering) of model
K1
K2
K3
K4

50. Implementing Finite Difference Modeling
Model Set-Up, Sensitivity Analysis,
Calibration and Prediction
Model Set-Up
Develop a Conceptual Model
Collect Data
Develop Mathematical Representation of your System
Model set-up is an Iterative process
Start simple and make sure the model runs after every
added complexity
Make Back-ups

51. Implementation
Anatomy of a Hydrogeological Investigation
and accompanying report
Significance
Define the problem in lay-terms
Highlight the importance of the problem being addressed
Objectives
Define the specific objectives in technical terms
Description of site and general hydrogeology
This is a presentation of your conceptual model

52. Implementation
Anatomy of a Hydrogeological Investigation (cont.)
Methodology
Convert your conceptual model into mathematical models that
will specifically address the Objectives
Determine specifically where you will get the information to
set-up the models
Results
Set up the models, calibrate, and use them to address the
objectives
Conclusions
Discuss specifically, and concisely, how your results achieved
the Objectives (or not)
If not, discuss improvements on the conceptual model and
mathematical representations

53. Developing a Conceptual Model
Settling Pond Example*
Questions to be addressed: (Objectives)
How much flow can Pond 1 receive
without overflowing? Q?
How long will water (contamination)
take to reach Pond 2 on average?v?
How much contaminant mass will enter
Pond 2 (per unit time)?
M?
A company has installed two settling ponds to: (Significance)
Settle suspended solids from effluent
Filter water before it discharges to stream
Damp flow surges
*This is a hypothetical example based on a composite of a few real cases
5000 ft
652
658
0
N
Pond 1
Pond 2

54. Conceptual Model (cont.)
Develop your conceptual model
W
1510
ft
x =186
Pond 1 Pond 2
Outfall
Elev.=
658.74 ft
Elev.=
652.23 ft
Q? v? M?
K
x =186 ft
b=8.56 ft
Water flows between ponds through
the saturated fine sand barrier driven
by the head difference
Sand
Clay
h=6.51 ft
Contaminated
Pond
b
x
Not to scale
Overflow

55. Conceptual Model (cont.)
Develop your mathematical representation (model)
(i.e., convert your conceptual model into a mathematical model)
Formulate reasonable assumptions
Saturated flow (constant hydraulic conductivity)
Laminar flow (a fundamental Darcy’s Law assumption)
Parallel flow (so you can use 1-D Darcy’s law)
Formulate a mathematical representation of your conceptual model
that:
Meets the assumptions and
Addresses the objectives
M = Q C
Q? v? M?

56. Conceptual Model (cont.)
Collect data to complete your Conceptual Model and to
Set up your Mathematical Model
The model determines the data to be collected
Cross sectional area (A = w b)
w: length perpendicular to flow
b: thickness of the permeable unit
Hydraulic gradient (h/x)
h: difference in water level in ponds
x: flow path length, width of barrier
Hydraulic Parameters
K: hydraulic tests and/or laboratory tests
n: estimated from grainsize and/or laboratory tests
Sensitivity analysis
Which parameters influence the results most strongly?
Which parameter uncertainty lead to the most uncertainty in the results?
x
h
A
K
Q




x
h
n
K
v




M = Q C
Q?
v?
M?

57. Implementing Finite Difference Modeling
Testing and Sensitivity Analysis
Adjust parameters and boundary conditions to get realistic
results
Test each parameter to learn how the model reacts
Gain an appreciation for interdependence of parameters
Document how each change effected the head distribution (and
heads at key points in the model)

58. Implementation (cont.)
Calibration
“Fine tune” the model by minimizing the error
Quantify the difference between the calculated and the
measured heads (and flows)
Mean Absolute Error Minimize
Calibration Plot
Allows identification of trouble spots
Calebration of a transient model
requires that the model be calibrated
over time steps to a transient event
e.g., pump test or rainfall episode
Automatic Calibration allows
parameter estimation
e.g., ModflowP
Measured Head
Calculated
Head
x
x
o
o
x
x
x
x
MW28dx
C
a
l
c
u
l
a
t
e
d
=
M
e
a
s
u
r
e
d

59. Implementation (cont.)
Prediction
A well calibrated model can be used to perform
reliable “what if” investigations
Effects of pumping on
Regional heads
Induced infiltration
Inter aquifer flow
Flow paths
Effects of urbanization
Reduced infiltration
Regional use of ground water
Addition and diversion of drainage

60. Case Study
An unconfined sand aquifer in northwest Ohio
Conceptual Model

61. Case Study
An unconfined sand aquifer in northwest Ohio
Surface water hydrology and topography

62. Boundary Conditions