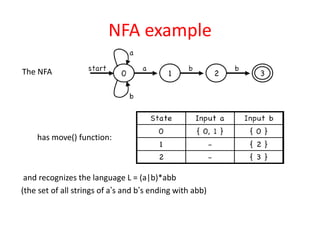
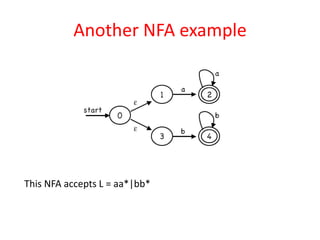
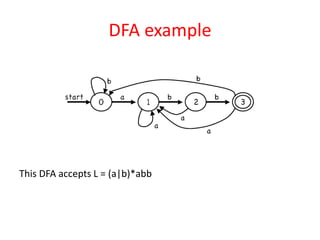
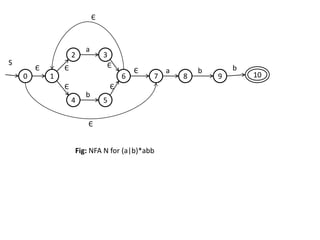
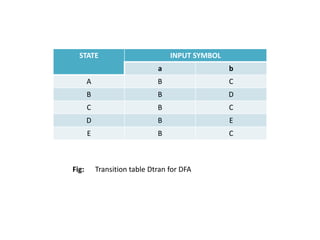
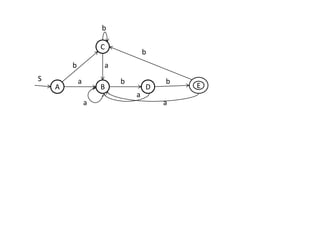
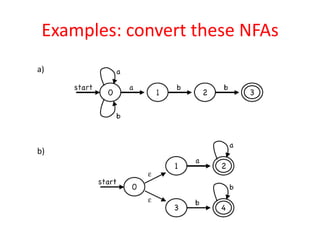
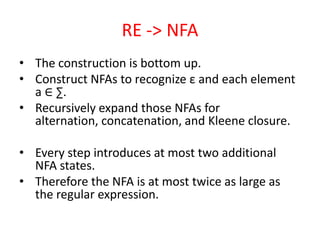
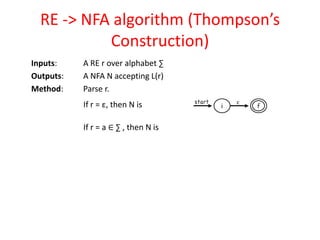
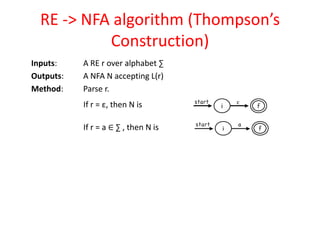
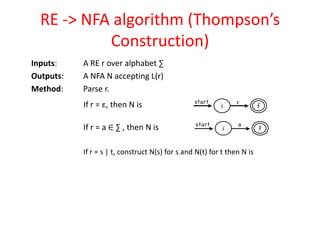
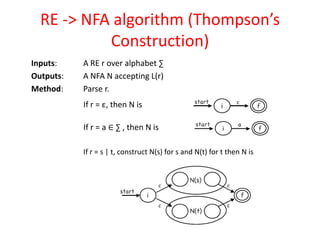
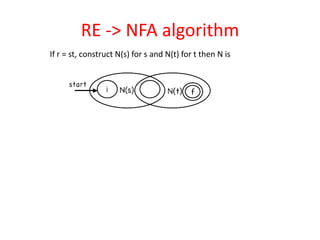
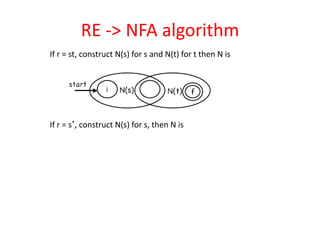
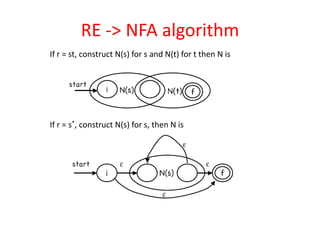
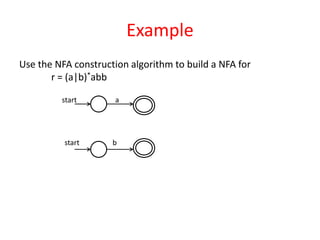
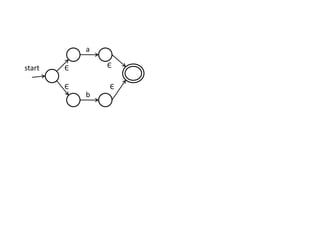
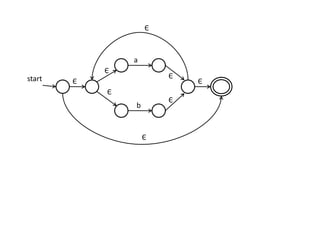
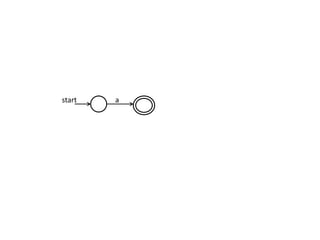
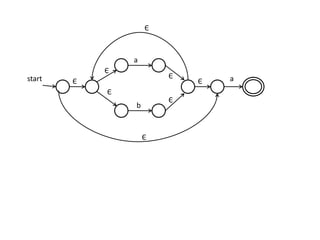
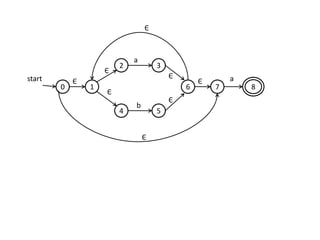
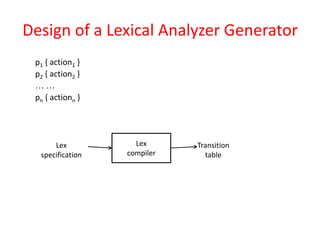
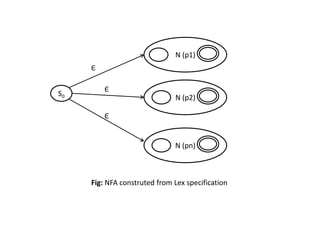
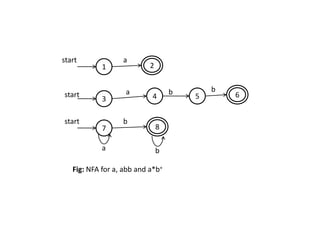
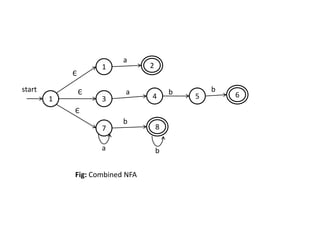
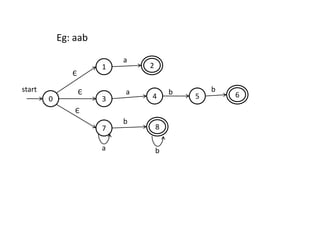
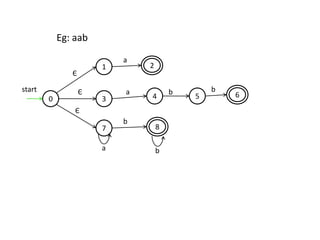
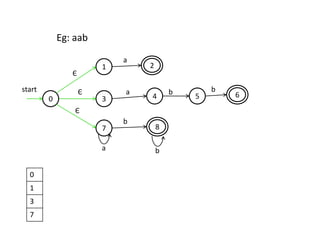
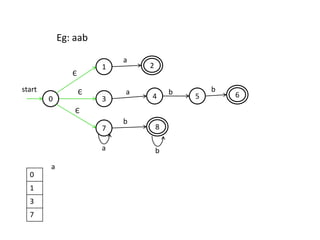
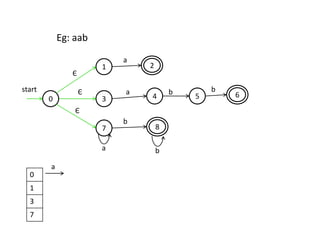
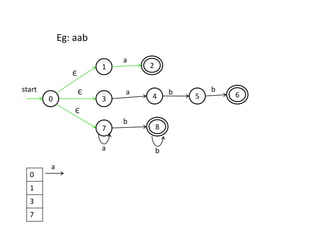
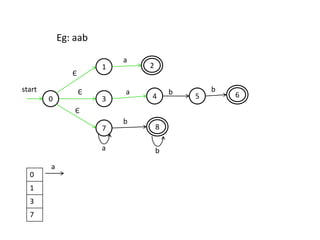
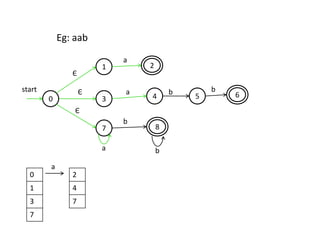
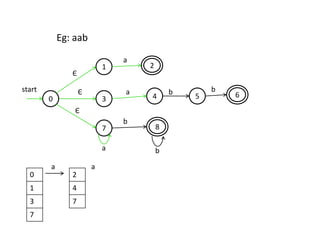
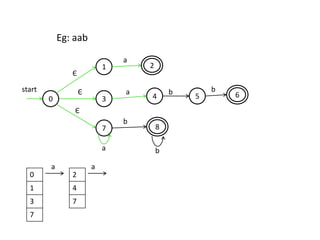
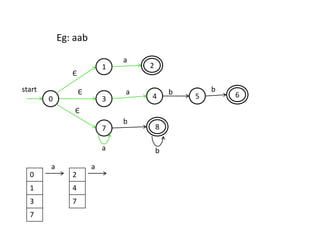
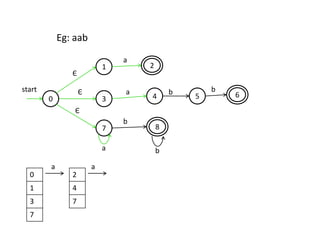
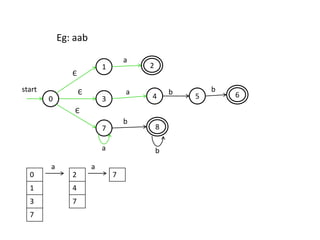
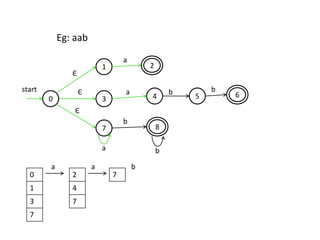
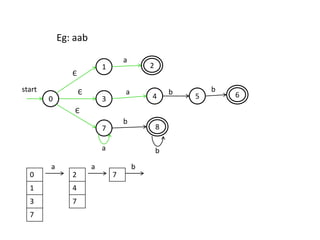
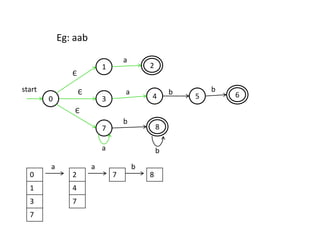
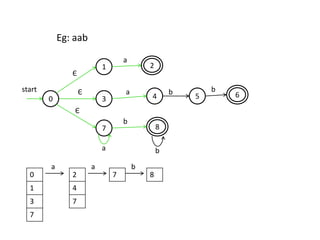
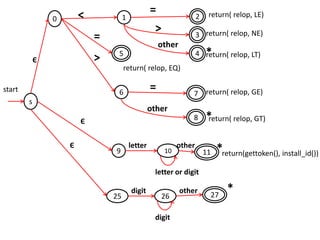
The document discusses finite automata and their application in lexical analysis, focusing on the generation of lexical analyzers from regular expressions. It explains the transformation from regular expressions to nondeterministic finite automata (NFA), and then to deterministic finite automata (DFA), detailing the characteristics and transition functions involved. Additionally, it outlines the construction algorithms for NFAs based on regex syntax and emphasizes their role in recognizing regular languages.

1. Finite Automata for Lexical Analysis

2. Automatic lexical analyzer generation
• How do Lex and similar tools do their job?
– Lex translates regular expressions into transition
diagrams.
– Then it translates the transition diagrams into C
code to recognize tokens in the input stream.
• There are many possible algorithms.
• The simplest algorithm is RE -> NFA -> DFA -> C code.

3. Finite automata (FAs) and regular
languages
• A RECOGNIZER takes language L and string x as
input, and responds YES if x∈L, or NO otherwise.
• The finite automaton (FA) is one class of recognizer.
• A FA is DETERMINISTIC if there is only one possible
transition for each <state,input> pair.
• A FA is NONDETERMINISTIC if there is more than one
possible transition some <state,input> pair.
• BUT both DFAs and NFAs recognize the same class of
languages: REGULAR languages, or the class of
languages that can be written as regular expressions.

4. NFAs
• A NFA is a 5-tuple < S, ∑, move, s0, F >
• S is the set of STATES in the automaton.
• ∑ is the INPUT CHARACTER SET
• move( s, c ) = S is the TRANSITION FUNCTION
specifying which states S the automaton can
move to on seeing input c while in state s.
• s0 is the START STATE.
• F is the set of FINAL, or ACCEPTING STATES

5. NFA example
The NFA
has move() function:
and recognizes the language L = (a|b)*abb
(the set of all strings of a’s and b’s ending with abb)

6. The language defined by a NFA
• An NFA ACCEPTS string x iff there exists a path
from s0 to an accepting state, such that the
edge labels along the path spell out x.
• The LANGUAGE DEFINED BY a NFA N, written
L(N), is the set of strings it accepts.

7. Another NFA example
This NFA accepts L = aa*|bb*

8. Deterministic FAs (DFAs)
The DFA is a special case of the NFA except:
– No state has an ε-transition
– No state has more than one edge leaving it for the
same input character.
The benefit of DFAs is that they are simple to simulate: there is
only one choice for the machine’s state after each input
symbol.

9. DFA example
This DFA accepts L = (a|b)*abb

10. RE -> DFA
• Now we know how to simulate DFAs.
• If we can convert our REs into a DFA, we can
automatically generate lexical analyzers.
• BUT it is not easy to convert REs directly into a
DFA.
• Instead, we will convert our REs to a NFA then
convert the NFA to a DFA.

11. Converting a NFA to a DFA

12. NFA -> DFA
• NFAs are ambiguous: we don’t know what state a NFA is in after observing
each input.
• The simplest conversion method is to have the DFA track the SUBSET of
states the NFA MIGHT be in.
• We need three functions for the construction:
– ε-closure(s): the set of NFA states reachable from NFA state s on ε-
transitions alone.
– ε-closure(T): the set of NFA states reachable from some state s ∈ T on
ε-transitions alone.
– move(T,a): the set of NFA states to which there is a transition on input
a from some NFA state s ∈ T

13. 0 1
2 3
4 5
6 7 8 9 10
S
Є Є
Є
a
Є
Є
Є
b
Є
Є a b b
Fig: NFA N for (a|b)*abb

14. 1) Є-closure (0) = {0,1,2,4,7} = A

15. 1) Є-closure (0) = {0,1,2,4,7} = A
Mark A.

16. 1) Є-closure (0) = {0,1,2,4,7} = A
Mark A.
∑ = {a, b}

17. 1) Є-closure (0) = {0,1,2,4,7} = A
Mark A.
∑ = {a, b}
2) Є-closure (move (A,a)) = Є-closure ( move ( {0,1,2,4,7}, a))

18. 1) Є-closure (0) = {0,1,2,4,7} = A
Mark A.
∑ = {a, b}
2) Є-closure (move (A,a)) = Є-closure ( move ( {0,1,2,4,7}, a))
= Є-closure ({3,8})

19. 1) Є-closure (0) = {0,1,2,4,7} = A
Mark A.
∑ = {a, b}
2) Є-closure (move (A,a)) = Є-closure ( move ( {0,1,2,4,7}, a))
= Є-closure ({3,8})
= {1,2,3,4,6,7,8} = B

20. 1) Є-closure (0) = {0,1,2,4,7} = A
Mark A.
∑ = {a, b}
2) Є-closure (move (A,a)) = Є-closure ( move ( {0,1,2,4,7}, a))
= Є-closure ({3,8})
= {1,2,3,4,6,7,8} = B
3) Є-closure (move (A, b)) = Є-closure ( move( {0,1,2,4,7},b))

21. 1) Є-closure (0) = {0,1,2,4,7} = A
Mark A.
∑ = {a, b}
2) Є-closure (move (A,a)) = Є-closure ( move ( {0,1,2,4,7}, a))
= Є-closure ({3,8})
= {1,2,3,4,6,7,8} = B
3) Є-closure (move (A, b)) = Є-closure ( move( {0,1,2,4,7},b))
= Є-closure ({5})

22. 1) Є-closure (0) = {0,1,2,4,7} = A
Mark A.
∑ = {a, b}
2) Є-closure (move (A,a)) = Є-closure ( move ( {0,1,2,4,7}, a))
= Є-closure ({3,8})
= {1,2,3,4,6,7,8} = B
3) Є-closure (move (A, b)) = Є-closure ( move( {0,1,2,4,7},b))
= Є-closure ({5})
= {1,2,4,5,6,7} = C

23. STATE INPUT SYMBOL
a b
A B C
B B D
C B C
D B E
E B C
Fig: Transition table Dtran for DFA

24. A
C
DB E
S
b
a
a
b
b
b b
a
a
a

25. Examples: convert these NFAs
a)
b)

26. Converting a RE to a NFA

27. RE -> NFA
• The construction is bottom up.
• Construct NFAs to recognize ε and each element
a ∈ ∑.
• Recursively expand those NFAs for
alternation, concatenation, and Kleene closure.
• Every step introduces at most two additional
NFA states.
• Therefore the NFA is at most twice as large as
the regular expression.

28. RE -> NFA algorithm (Thompson’s
Construction)
Inputs: A RE r over alphabet ∑
Outputs: A NFA N accepting L(r)
Method: Parse r.

29. RE -> NFA algorithm (Thompson’s
Construction)
Inputs: A RE r over alphabet ∑
Outputs: A NFA N accepting L(r)
Method: Parse r.
If r = ε, then N is

30. RE -> NFA algorithm (Thompson’s
Construction)
Inputs: A RE r over alphabet ∑
Outputs: A NFA N accepting L(r)
Method: Parse r.
If r = ε, then N is

31. RE -> NFA algorithm (Thompson’s
Construction)
Inputs: A RE r over alphabet ∑
Outputs: A NFA N accepting L(r)
Method: Parse r.
If r = ε, then N is
If r = a ∈ ∑ , then N is

32. RE -> NFA algorithm (Thompson’s
Construction)
Inputs: A RE r over alphabet ∑
Outputs: A NFA N accepting L(r)
Method: Parse r.
If r = ε, then N is
If r = a ∈ ∑ , then N is

33. RE -> NFA algorithm (Thompson’s
Construction)
Inputs: A RE r over alphabet ∑
Outputs: A NFA N accepting L(r)
Method: Parse r.
If r = ε, then N is
If r = a ∈ ∑ , then N is
If r = s | t, construct N(s) for s and N(t) for t then N is

34. RE -> NFA algorithm (Thompson’s
Construction)
Inputs: A RE r over alphabet ∑
Outputs: A NFA N accepting L(r)
Method: Parse r.
If r = ε, then N is
If r = a ∈ ∑ , then N is
If r = s | t, construct N(s) for s and N(t) for t then N is

35. RE -> NFA algorithm
If r = st, construct N(s) for s and N(t) for t then N is

36. RE -> NFA algorithm
If r = st, construct N(s) for s and N(t) for t then N is

37. RE -> NFA algorithm
If r = st, construct N(s) for s and N(t) for t then N is
If r = s*, construct N(s) for s, then N is

38. RE -> NFA algorithm
If r = st, construct N(s) for s and N(t) for t then N is
If r = s*, construct N(s) for s, then N is

39. Example
Use the NFA construction algorithm to build a NFA for
r = (a|b)*abb
start a
start b

40. Є
Є
a
Є
Є
b
start

41. Є
Є
a
Є
Є
b
Єstart
Є
Є
Є

42. start a

43. Є
Є
a
Є
Є
b
Єstart
Є
Є
Є
a

44. 1
2 3
4 5
Є
Є
a
Є
Є
b
6
Є
0
start
Є
Є
Є
7 8
a

45. Design of a Lexical Analyzer Generator
p1 { action1 }
p2 { action2 }
… …
pn { actionn }
Lex
compiler
Lex
specification
Transition
table

46. lexeme
FA
simulator
Transition
table
input buffer

47. S0
N (p1)
N (p2)
N (pn)
Є
Є
Є
Fig: NFA construted from Lex specification

48. For eg:
a
abb
a*b+

49. 1
3
7
2
54 6
8
start
start
start
a
a
a
b
b
b b
Fig: NFA for a, abb and a*b+

50. 1
3
7
2
54 6
8
start
a
a
a
b
b
b b
1
Є
Є
Є
Fig: Combined NFA

51. 1
3
7
2
54 6
8
start
a
a
a
b
b
b b
0
Є
Є
Є
Eg: aab

52. 1
3
7
2
54 6
8
start
a
a
a
b
b
b b
0
Є
Є
Є
Eg: aab

53. 1
3
7
2
54 6
8
start
a
a
a
b
b
b b
0
Є
Є
Є
Eg: aab
0
1
3
7

54. 1
3
7
2
54 6
8
start
a
a
a
b
b
b b
0
Є
Є
Є
Eg: aab
0
1
3
7
a

55. 1
3
7
2
54 6
8
start
a
a
a
b
b
b b
0
Є
Є
Є
Eg: aab
0
1
3
7
a

56. 1
3
7
2
54 6
8
start
a
a
a
b
b
b b
0
Є
Є
Є
Eg: aab
0
1
3
7
a

57. 1
3
7
2
54 6
8
start
a
a
a
b
b
b b
0
Є
Є
Є
Eg: aab
0
1
3
7
a

58. 1
3
7
2
54 6
8
start
a
a
a
b
b
b b
0
Є
Є
Є
Eg: aab
0
1
3
7
2
4
7
a

59. 1
3
7
2
54 6
8
start
a
a
a
b
b
b b
0
Є
Є
Є
Eg: aab
0
1
3
7
2
4
7
a a

60. 1
3
7
2
54 6
8
start
a
a
a
b
b
b b
0
Є
Є
Є
Eg: aab
0
1
3
7
2
4
7
a a

61. 1
3
7
2
54 6
8
start
a
a
a
b
b
b b
0
Є
Є
Є
Eg: aab
0
1
3
7
2
4
7
a a

62. 1
3
7
2
54 6
8
start
a
a
a
b
b
b b
0
Є
Є
Є
Eg: aab
0
1
3
7
2
4
7
a a

63. 1
3
7
2
54 6
8
start
a
a
a
b
b
b b
0
Є
Є
Є
Eg: aab
0
1
3
7
2
4
7
7
a a

64. 1
3
7
2
54 6
8
start
a
a
a
b
b
b b
0
Є
Є
Є
Eg: aab
0
1
3
7
2
4
7
7
a a b

65. 1
3
7
2
54 6
8
start
a
a
a
b
b
b b
0
Є
Є
Є
Eg: aab
0
1
3
7
2
4
7
7
a a b

66. 1
3
7
2
54 6
8
start
a
a
a
b
b
b b
0
Є
Є
Є
Eg: aab
0
1
3
7
2
4
7
7 8
a a b

67. 1
3
7
2
54 6
8
start
a
a
a
b
b
b b
0
Є
Є
Є
Eg: aab
0
1
3
7
2
4
7
7 8
a a b

68. 0 21
6
3
45
7
8
start
< =
>
other
return( relop, LE)
return( relop, NE)
return( relop, LT)
return( relop, EQ)
return( relop, GE)
return( relop, GT)
other
=
*
*
=
>
9 10 11
Є
letter
letter or digit
other
*return(gettoken(), install_id())
25 26 27
digit
digit
other *
Є
s
Є