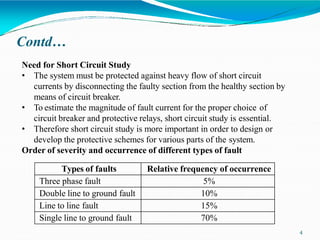
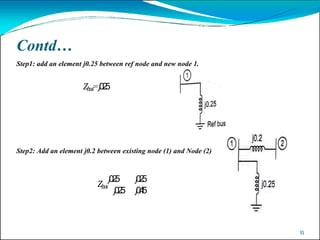
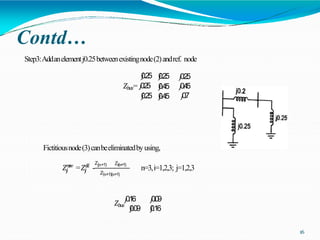
1) The document discusses fault analysis and short circuit studies, which are important for designing protective schemes for power systems. It defines different types of faults like symmetrical, shunt, series, and explains their characteristics. 2) Bus impedance matrix calculation methods like bus building algorithm are explained. The algorithm allows modification of the matrix when network changes without complete rebuilding. 3) An example demonstrates using the bus building algorithm to determine the bus impedance matrix for a sample network. Assumptions and applications of short circuit studies in protection are also summarized.

1. 1
SWAMI PARMANAND COLLEGE OF
ENGINEERING & TECHNOLOGY
SEMINAR
ON
FAULT ANALYSIS
Submitted To:- Submitted By:-
Er. Kapil Sethi Murari Shaw
H.O.D of E.E.E Deptt. Roll No:-1611804
Sem. EEE Branch/ 7th

2. Introduction
2
The fault is called symmetrical fault if the fault current is equal
in all the three phases.
This fault conditions are analyzed on per phase basis using
Thevenin's theorem or bus impedance matrix. The three phase
fault is the only symmetrical fault.
Classification:
Shunt Faults:
Three phase faults
Line to ground fault
Line to line fault
Double line to ground fault

3. Contd….
3
Shunt fault is characterized by minimum voltage and maximum
current.
Series Faults
Open conductor fault
Two open conductor fault.
Series fault is characterized by maximum voltage and minimum
current.
Bolted fault or solid fault
A fault represents a structural network change equivalent with that
caused by the addition of impedance at the place of fault. If the fault
impedance is zero, then the fault is referred as bolted fault or solid fault.

4. Contd…
4
Types of faults Relative frequency of occurrence
Three phase fault 5%
Double line to ground fault 10%
Line to line fault 15%
Single line to ground fault 70%
Need for Short Circuit Study
• The system must be protected against heavy flow of short circuit
currents by disconnecting the faulty section from the healthy section by
means of circuit breaker.
• To estimate the magnitude of fault current for the proper choice of
circuit breaker and protective relays, short circuit study is essential.
• Therefore short circuit study is more important in order to design or
develop the protective schemes for various parts of the system.
Order of severity and occurrence of different types of fault

5. Contd….
5
Fault calculations
The fault condition of a power system can be divided into transient,
subtransient and steady state periods. The currents in the various parts of the
power system and in the fault are different in these periods. The estimation of
these currents for various types of faults at various locations in the system are
commonly referred to as fault calculations.
Assumptions to be made to simplify the short circuit study:
Representing each machine by constant voltage source behind proper
reactances.
Prefault load currents are neglected
Transformer taps are assumed to be nominal.
Shunt elements in the transformer model that accounting for magnetizing
current and core losses are neglected.
Shunt capacitance of the transmission line is ignored.
Series resistance of transmission lines is neglected.

6. Short circuit capacity(SSC).
The short circuit capacity at a bus is defined as the product of the
magnitudes of the prefault bus voltages and post fault current.
Short Circuit MVA(3φ)= 𝑉 𝑝𝑟𝑒𝑓𝑎𝑢𝑙𝑡* 𝐼𝑠𝑐*𝑀𝑉𝐴𝑏
SSC used to determine the dimensions of the bus bar and interrupting
capacity of the circuit breaker.
Direct axis reactance
It is the ratio of induced emf and the steady state RMScurrent.
Subtransient reactance
It is the ratio of induced emf on no load and the subtransient
symmetrical RMS current.
The subtransient reactance can be used to estimate the initial value of
fault current immediately on the occurrence of the fault. The
maximum momentary short circuit current rating of the circuit
breaker used for protection should be less than this faultcurrent.
6

7. Contd…
Transient reactance
It is the ratio of induced emf on no load and the transient
symmetrical RMS current.
′′
𝑋
𝐸𝑔
𝑑 𝐼
′ ′
The transient reactance is used to estimate the transient state fault
current. Most of the circuit breakers open their contacts only
during this period. Therefore a circuit breaker used for fault
clearing, its interrupting short circuit current rating should be
less than transient fault current.
7

8. Bus impedance Matrix
Bus Impedance 𝑍𝑏𝑢𝑠= 𝑌𝑏𝑢𝑠
−1
𝑍𝑏𝑢𝑠=
𝑍21
8
𝑍11 𝑍12
𝑍22
⋮ ⋮
𝑍𝑛1 𝑍𝑛2
…
…
⋱
…
𝑍1𝑛
𝑍2𝑛
⋮
𝑍𝑛𝑛
n*n for n bus system
 The diagonal elements are short circuit driving point impedancesand
off-diagonal elements are short circuit transfer admittances.
 𝑍𝑏𝑢𝑠 is symmetric when 𝑌𝑏𝑢𝑠is symmetric.
 𝑍𝑏𝑢𝑠 is a fullmatrix.
 𝑍𝑏𝑢𝑠 is used for symmetrical and unsymmetrical faultanalysis.
Two methods:
1. Bus building algorithm
2. L-U Factorization of 𝑌𝑏𝑢𝑠

9. Bus building Algorithm for Bus Impedance
Matrix
9
Advantages:
Any modification of the network does not require complete rebuilding of
𝑍𝑏𝑢𝑠.
Easily computerized.
Assume a original 𝑍𝑏𝑢𝑠 matrix with n nodes. It is proposed to add new
elements, one at a time to this network and get the modified 𝑍𝑏𝑢𝑠 matrix.
Modification1: Add an element with impedance Z, connected between the
reference node and a new node (n+1).
Modification2: Add an element, connected between an existing node I and
a new node n+i.
Modification 3: Add an element, connected between an existing node i and
the reference node.
Modification 4: Add an element connected between existing nodes I and j.

10. Contd….
𝑛𝑒
𝑤
𝑍𝑏𝑢𝑠 =
Rule 1: Add an element with impedance Z, connected between the reference
node and a new node (n+1)
Consider an impedance Z is connected between the reference node and the
new node (n+1).
The addition of a bus will increase the order of the bus impedance matrix by
one. The modified 𝑍𝑏𝑢𝑠 matrix is givenby,
𝑍𝑜𝑙𝑑
10
…
⋮ 0
𝑏𝑢𝑠
0
⋯
⋮ 𝑍

11. Contd…
Rule 2: Add an element with impedance Z, connected between an existing
node i and a new node (n+1).
Consider an impedance Z is connected between the existing node I and the
new node (n+1).
The addition of a bus will increase the order of the bus impedance matrix by
one.
The modified 𝑍𝑏𝑢𝑠 matrix is givenby,
𝑏𝑢𝑠
𝑍𝑛𝑒𝑤
=
𝑍𝑜𝑙𝑑
11
𝑏𝑢𝑠
……
⋮
𝑍𝑖
…
𝑖
𝑍𝑇
𝑍 +𝑍𝑖𝑖

12. Contd…
Rule 3: Add an element with impedance Z, connected between an existing
node i and the reference node.
The first step is to add an element in between the existing node I and a
fictitious node (n+1) and obtain the modified 𝑍𝑏𝑢𝑠 matrix of dimension
(n+1)*(n+1).
The second step is connect the fictitious node (n+1) by zero matrix link to
the reference node whose voltage is zero.
To obtain the new modified 𝑍𝑏𝑢𝑠 matrix of dimension n*n by applying
Kron’s reduction to the last row and column using the relation,
𝑗
𝑘𝑏𝑢𝑠
𝑍
𝑚
= 𝑍𝑗𝑘-
𝑍𝑗(𝑛+1) 𝑍𝑘(𝑛+1)
𝑍 𝑛+1 (𝑛+1)
j,k=1,2,….n
12

13. Contd…
Rule 4: Add an element with impedance Z, connected betweenexisting
nodes i and j.
Connect an element Z, connected between two existing buses (i and j),
the new modified 𝑍𝑏𝑢𝑠 matrix is givenby,
Now the size of the matrix becomes (n+1)*(n+1). To obtain the new
modified 𝑍𝑏𝑢𝑠 matrix of dimension n*n by applying Kron’s reduction to
the last row and column using,
𝑗𝑘𝑏𝑢𝑠
𝑍
𝑚
=𝑍𝑗
𝑘
𝑍𝑗(𝑛+1) 𝑍𝑘(𝑛+1)
- 𝑍 𝑛+1 (𝑛+1)
j,k=1,2,….n
13

14. Example:
Using building algorithm method, determine ZBus for the network shown in figure,
where the impedances labeled are shown in per unit.
Solution:
J0.1 and j0.1 are connected in series
Z=j0.2
14

15. Contd…
15
𝑍𝑏
𝑢
𝑠=𝑗
0
.
2
5
𝑍𝑏
𝑢
𝑠
𝑗
0
.
2
5
𝑗
0
.
2
5 𝑗
0
.
4
5
𝑗
0
.
2
5
Step1: add an element j0.25 between ref node and new node 1.
Step2: Add an element j0.2 between existing node (1) and Node (2)

16. Contd…
Step3:Addanelementj0.25betweenexistingnode(2)andref. node
𝑗
0.25
𝑍𝑏𝑢𝑠= 𝑗
0
.2
5
𝑗
0.25
𝑗
0.25
𝑗
0.45
𝑗
0.45
𝑗
0
.2
5
𝑗
0
.4
5
𝑗
0
.
7
Fictitiousnode(3)canbeeliminatedbyusing,
𝑖
𝑗 𝑖
𝑗
𝑛
𝑒
𝑤 𝑜
𝑙
𝑑
𝑍 =𝑍 -
𝑍𝑗
(𝑛+1) 𝑍𝑖(𝑛+1)
𝑍(𝑛+1)(𝑛+1)
n=3,i=1,2,3; j=1,2,3
16
𝑍𝑏𝑢𝑠
𝑗
0
.1
6
𝑗
0.09 𝑗
0.16
𝑗
0
.0
9

17. Contd…
Step4:Addanelementj0.2betweentheexistingnodes(1)and (2).
𝑗
0.16
𝑍𝑏𝑢𝑠= 𝑗0.09
𝑗0.07
𝑗0.09
𝑗0.16
−
𝑗
0.07
𝑗0.07
−𝑗0.07
𝑗0.34
Fictitiousnode(3)canbeeliminatedbyusing,
𝑍𝑖
𝑗 𝑖
𝑗
𝑛𝑒
𝑤 𝑜
𝑙
𝑑
=𝑍 -
𝑍𝑗
(𝑛+1) 𝑍𝑖(𝑛+1)
𝑍(𝑛+1)(𝑛+1)
n=3,i=1,2,3; j=1,2,3
17
𝑍𝑏𝑢𝑠
𝑗0.146
𝑗0.104 𝑗0.146
𝑗0.104

18. Conclusion:
18
The need and assumptions for short circuit study is listed and the z-bus
building algorithm is explained with an example.
References:
1. Hadi Saadat, ‘Power System Analysis’, Tata McGraw Hill Education Pvt. Ltd.,
New Delhi, 21st reprint, 2010.
2. Kundur P., ‘Power System Stability and Control, Tata McGraw Hill Education Pvt.
Ltd., New Delhi, 10th reprint, 2010.
3. Pai M A, ‘Computer Techniques in Power System Analysis’, Tata Mc Graw- Hill
Publishing
Company Ltd., New Delhi, Second Edition, 2007.
4. J. Duncan Glover, Mulukutla S. Sarma, Thomas J. Overbye, ‘ PowerSystem
Analysis & Design’, Cengage Learning, Fifth Edition, 2012.
5. Olle. I. Elgerd, ‘Electric Energy Systems Theory – An Introduction’, Tata McGraw
Hill Publishing Company Limited, New Delhi, Second Edition, 2012.
6. C.A.Gross, “Power System Analysis,” Wiley India, 2011.
7. M.Jeraldin Ahila “Power System Analysis”, Lakshmi Publications, Chennai,
Eleventh Edition 2017.
8. Other web sources