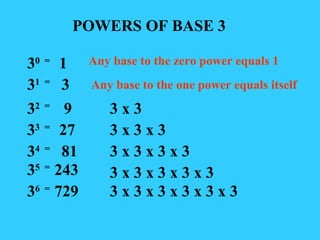
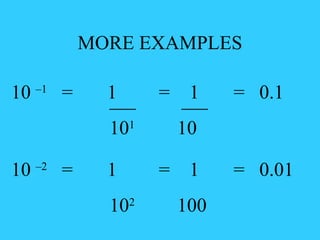The document discusses exponents and properties of exponents. It defines exponents and provides examples of evaluating exponents using multiplication, division, and negative exponents. Specifically, it explains that the base is multiplied when exponents are added, divided when exponents are subtracted, and that a negative exponent is the same as the reciprocal of the positive form with the exponent as the denominator.

1. EXPONENTS Zero and Negative

2. X 2 X TO THE SECOND POWER OR X SQUARED X IS CALLED BASE 2 IS CALLED EXPONENT Use x as a factor 2 times X * X

3. X 3 X TO THE THIRD POWER OR X CUBED X IS CALLED BASE 3 IS CALLED EXPONENT Use x as a factor 3 times X * X *X

4. X 4 X TO THE FOURTH POWER X IS CALLED BASE 4 IS CALLED EXPONENT Use x as a factor 4 times X * X * X * X

5. 3 2 3 TO THE SECOND POWER OR 3 SQUARED Use 3 as a factor 2 times 3 * 3 3 2 = 9

6. 3 3 3 TO THE THIRD POWER OR 3 CUBED Use 3 as a factor 2 times 3 * 3 * 3 3 3 = 27

7. POWERS OF BASE 10 10 0 = 1 10 1 = 10 10 2 = 100 10 3 = 1000 10 4 = 10,000 10 5 = 100,000 10 6 = 1,000,000

8. POWERS OF BASE 2 2 0 = 1 2 1 = 2 2 2 = 4 2 3 = 8 2 4 = 16 2 5 = 32 2 6 = 64 Any base to the zero power equals 1 Any base to the one power equals itself 2 x 2 2 x 2 x 2 2 x 2 x 2 x 2 2 x 2 x 2 x 2 x 2 2 x 2 x 2 x 2 x 2 x 2

9. POWERS OF BASE 3 3 0 = 1 3 1 = 3 3 2 = 9 3 3 = 27 3 4 = 81 3 5 = 243 3 6 = 729 Any base to the zero power equals 1 Any base to the one power equals itself 3 x 3 3 x 3 x 3 3 x 3 x 3 x 3 3 x 3 x 3 x 3 x 3 3 x 3 x 3 x 3 x 3 x 3

10. TRY IT OUT 10 0 = 1 5 0 = 1 2 3 = 8 3 4 = 81 5 3 = 125 2 5 = 32

11. TRY IT OUT 10 3 = 16 0 = 1 6 2 = 36 5 2 = 25 4 3 = 64 7 3 = 343 1000

12. MULTIPLYING EXPONENTS WITH THE SAME BASE

13. X 2 * X 3 = X 5 X * X * X * X* X Keep the base ADD the Exponents

14. (10 2 ) (10 3 ) = 10 5 10 * 10 * 10 * 10* 10 Keep the base ADD the Exponents () () PARENTHESES mean TIMES

15. (Y 3 X 2 ) (Y 4 X 3 ) = Y 7 X 5 ( Y * Y * Y * X * X ) * ( Y * Y* Y * Y * X * X * X) Keep the base ADD the Exponents () () PARENTHESES mean TIMES

16. TRY IT OUT 5 * 5 2 * 5 3 = 5 6 Don’t forget the one exponent is implied X * Y 2 * X 3 * Y = X 4 Y 3 Don’t forget the one exponent is implied

17. TRY IT OUT (XY 3 ) ( X 2 Y 3 ) = X 3 Y 6 Don’t forget the one exponent is implied (X 2 Y 2 Z 3 ) (Y 4 Z 5 ) = X 2 Y 6 Z 8 Don’t forget the one exponent is implied

18. DIVIDING EXPONENTS WITH THE SAME BASE

19. X 5 / X 3 = X 2 Keep the base SUBTRACT the Exponents

20. 10 6 / 10 2 = 10 4 Keep the base SUBTRACT the Exponents

21. Negative Exponents Negative exponents are NOT negative numbers Negative exponents are fractions or decimals Negative exponents are greater than 0 but less than one

22. Examples 10 -3 = 1 10 3 OR 1 1000 OR 0.001

23. Examples 2 -3 = 1 2 3 OR 1 8 OR 0.125

24. Examples 2 -3 = 1 2 3 OR 1 8 OR 0.125 Negative Exponent To Reciprocal To Fraction To Decimal

25. MORE EXAMPLES 10 –1 = 1 = 1 = 0.1 10 1 10 10 –2 = 1 = 1 = 0.01 10 2 100

26. MORE EXAMPLES 10 –3 = 1 = 1 = 0.001 10 3 1000 10 –4 = 1 = 1 = 0.0001 10 4 10000

27. MORE EXAMPLES 10 –5 = 1 = 1 = 0.00001 10 5 100,000 10 –6 = 1 = 1 = 0.000001 10 6 1,000,000

28. Created by: pmastro.weebly.com/uploads/2/8/2/7/.../ exponents .801116. ppt