Download as PDF, PPTX
Uploaded byIsmail M. El-Badawy
Exponential growth
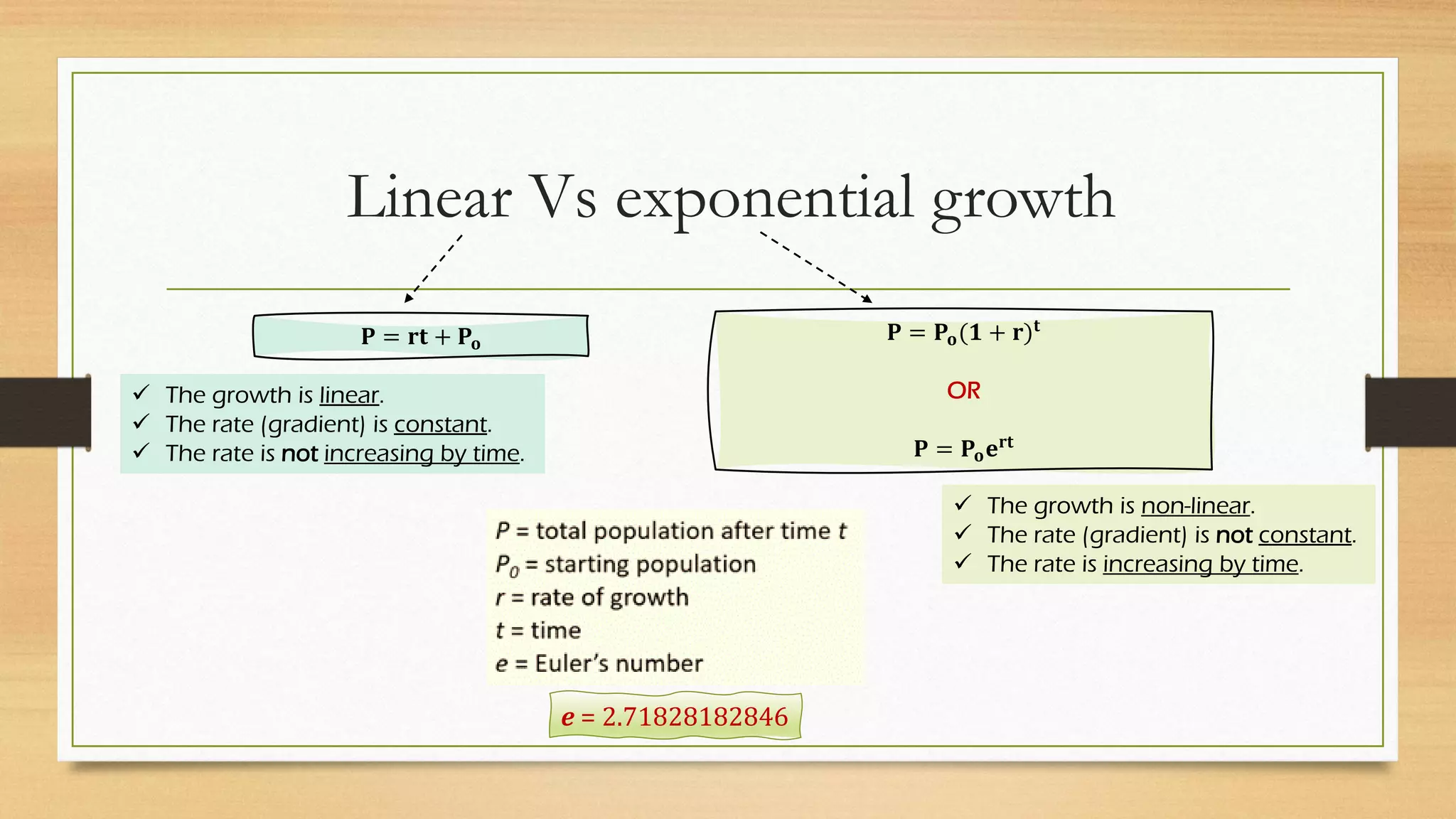
The document discusses the differences between linear and exponential growth, emphasizing that exponential growth features a non-constant rate that increases over time. It uses the population growth of bacteria and the 2009 H1N1 flu outbreak in Japan as case studies to illustrate these concepts and includes equations for calculating growth rates. The text concludes with a comparison of predictive models based on average error rates.
More Related Content
Similar to Exponential growth
Exponential growth
- 1. Exponential growth Prepared by IsmailMohammad El-Badawy ismailelbadawy@gmail.com
- 2. Linear Vs exponentialgrowth 𝐏 = 𝐫𝐭 + 𝐏𝐨 𝐏 = 𝐏𝐨(𝟏 + 𝐫)𝐭 OR 𝐏 = 𝐏𝐨 𝐞 𝐫𝐭 e = 2.71828182846 ✓ The growth is linear. ✓ The rate (gradient) is constant. ✓ The rate is not increasing by time. ✓ The growth is non-linear. ✓ The rate (gradient) is not constant. ✓ The rate is increasing by time.
- 3. Exponential growth • Populationgrowth is a common example of exponential growth. • Consider a population of bacteria, for instance: • It seems plausible that the rate of population growth would be proportional to the size of the population. • After all, the more bacteria there are to reproduce, the faster the population grows. • The figure shows the growth of a population of bacteria with an initial population of 200 bacteria and a rate of growth (growth constant) of 0.02. • Notice that after only 2 hours (120 minutes), the population is 10 times its original size! 200 ✓ The growth is non-linear. ✓ The rate (gradient) is not constant. ✓ The rate is increasing by time. e = 2.71828182846OR 𝐏 = 𝐏𝐨(𝟏 + 𝐫)𝐭
- 4. H1N1 flu outbreak2009 in Japan Time (days) Recorded cases 0 98 25 183 50 326 75 534 100 768 (25, 183) (50, 326) (75, 534) (100, 768) (0, 98) 𝐏 = 𝐏𝐨 𝐞 𝐫𝐭 𝐏 = 𝐏𝐨(𝟏 + 𝐫)𝐭 OR Let’s find the model Rate of change (Δy/Δx) is not fixed ……. That’s why a straight line cannot be used to model the data
- 5. Make r subjectof the formula P = Poert P = Po(1 + r)t
- 6. Make r subjectof the formula P = Poert P Po = ert ln P Po = ln ert ln P Po = rt ln e ln P Po = rt ∴ 𝐫 = 𝟏 𝐭 𝐥𝐧 𝐏 𝐏𝐨 P = Po(1 + r)t P Po = (1 + r)t Log P Po = Log(1 + r)t Log P Po = t Log 1 + r 1 t Log P Po = Log 1 + r 10 1 t log P Po = 1 + r ∴ 𝐫 = 𝟏𝟎 𝟏 𝐭 𝐥𝐨𝐠 𝐏 𝐏 𝐨 −𝟏
- 7. Let’s find themodel Time (days) Recorded cases Growth rate ‘ r ‘ 0 98 - 25 183 50 326 75 534 100 768 𝐫 = 𝟏 𝐭 𝐥𝐧 𝐏 𝐏𝐨 𝐏 = 𝐏𝐨 𝐞 𝐫𝐭
- 8. Let’s find themodel Time (days) Recorded cases Growth rate ‘ r ‘ 0 98 - 25 183 0.025 50 326 0.024 75 534 0.023 100 768 0.021 ✓ Average growth rate = 0.023 𝐫 = 𝟏 𝐭 𝐥𝐧 𝐏 𝐏𝐨 𝐏 = 𝐏𝐨 𝐞 𝐫𝐭 𝐏𝐨
- 9. 98 𝑒0.023𝑡 98 𝐏 =𝟗𝟖 𝐞 𝟎.𝟎𝟐𝟑𝐭 Time (days) Actual cases Predicted cases Error 0 98 25 183 50 326 75 534 100 768
- 10. 98 𝑒0.023𝑡 98 𝐏 =𝟗𝟖 𝐞 𝟎.𝟎𝟐𝟑𝐭 Time (days) Actual cases Predicted cases Error 0 98 98 0 25 183 174.16 8.84 50 326 309.50 16.5 75 534 550.03 -16.03 100 768 977.47 -209.47 𝐀𝐯𝐞𝐫𝐚𝐠𝐞 𝐚𝐛𝐬𝐨𝐥𝐮𝐭𝐞 𝐞𝐫𝐫𝐨𝐫 = 𝟎 + 𝟖. 𝟖𝟒 + 𝟏𝟔. 𝟓 + 𝟏𝟔. 𝟎𝟑 + 𝟐𝟎𝟗. 𝟒𝟕 𝟓 = 𝟓𝟎. 𝟏𝟔
- 11. Let’s find themodel Time (days) Recorded cases Growth rate ‘ r ‘ 0 98 - 25 183 50 326 75 534 100 768 𝐫 = 𝟏𝟎 𝟏 𝐭 𝐥𝐨𝐠 𝐏 𝐏 𝐨 − 𝟏 𝐏 = 𝐏𝐨(𝟏 + 𝐫)𝐭
- 12. Let’s find themodel Time (days) Recorded cases Growth rate ‘ r ‘ 0 98 - 25 183 0.025 50 326 0.024 75 534 0.023 100 768 0.021 ✓ Average growth rate = 0.023 𝐏𝐨 𝐏 = 𝐏𝐨(𝟏 + 𝐫)𝐭 𝐫 = 𝟏𝟎 𝟏 𝐭 𝐥𝐨𝐠 𝐏 𝐏 𝐨 − 𝟏
- 13. 98(1 + 0.023)𝑡 98 𝐏 = 𝟗𝟖(𝟏 + 𝟎. 𝟎𝟐𝟑)𝐭 Time (days) Actual cases Predicted cases Error 0 98 25 183 50 326 75 534 100 768
- 14. 98(1 + 0.023)𝑡 98 𝐏 = 𝟗𝟖(𝟏 + 𝟎. 𝟎𝟐𝟑)𝐭 Time (days) Actual cases Predicted cases Error 0 98 98 0 25 183 173.03 9.97 50 326 305.48 20.52 75 534 539.38 -5.38 100 768 952.33 -184.33 𝐀𝐯𝐞𝐫𝐚𝐠𝐞 𝐚𝐛𝐬𝐨𝐥𝐮𝐭𝐞 𝐞𝐫𝐫𝐨𝐫 = 𝟎 + 𝟗. 𝟗𝟕 + 𝟐𝟎. 𝟓𝟐 + 𝟓. 𝟑𝟖 + 𝟏𝟖𝟒. 𝟑𝟑 𝟓 = 𝟒𝟒. 𝟎𝟒
- 15. Which model shallyou choose ? 98 𝐏 = 𝟗𝟖𝐞 𝟎.𝟎𝟐𝟑𝐭 𝐏 = 𝟗𝟖(𝟏 + 𝟎. 𝟎𝟐𝟑)𝐭 OR Average error 50.16 44.04