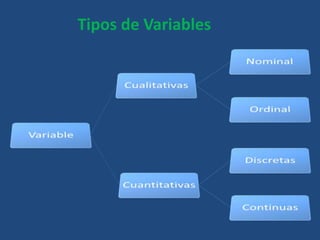
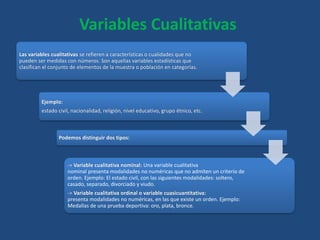
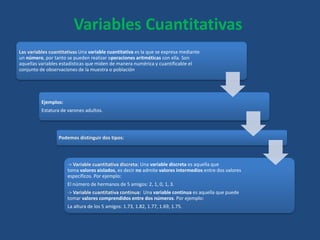
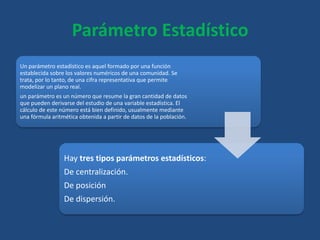
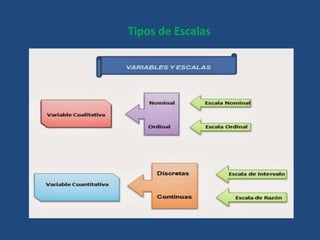
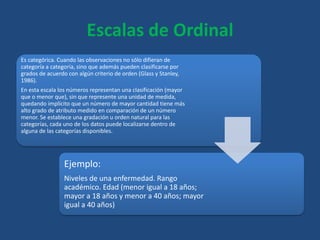
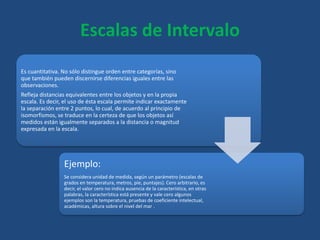
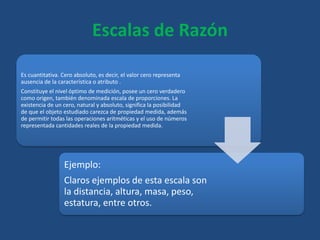
Este documento define conceptos básicos de estadística como variables, población, muestra, parámetros estadísticos, medidas de centralización, posición y dispersión. También explica los tipos de variables cualitativas y cuantitativas, y las escalas de medición nominal, ordinal, de intervalo y razón. Finalmente, incluye definiciones breves de tasa, frecuencia y proporción.

1. REPUBLICA BOLIVARIANA DE VENEZUELA
INSTITUTO UNIVERSITARIO POLITECNICO «SANTIAGO MARIÑO»
SEDE BARCELONA
INGENERIA SISTEMAS
ESTADISTICA I - SV
ESTADISTICA
Bachiller :
Davinson García C.I: 19.184.885
Profesor :
Ramón Aray

2. Definición de Variable
Una variable estadística es la representación matemática de un
carácter de tal manera que podrá tomar tantos valores como
modalidades presente el carácter correspondiente. Una
característica se clasifica como variable si, se encuentra que ésta
toma diferentes valores en los diferentes elementos de la muestra
o población en estudio, por lo tanto NO es constante. En otras
palabras, es una propiedad que puede fluctuar y cuya variación es
susceptible de medirse u observarse.
Ejemplos de variables:
• Presión sanguínea diastólica.
• Masa de niños en edad preescolar.
• Frecuencia cardiaca.
• Estatura de varones adultos.
• Edad de los pacientes de un médico.

3. Tipos de Variables

4. Las variables cualitativas se refieren a características o cualidades que no
pueden ser medidas con números. Son aquellas variables estadísticas que
clasifican el conjunto de elementos de la muestra o población en categorías.
Ejemplo:
estado civil, nacionalidad, religión, nivel educativo, grupo étnico, etc.
Podemos distinguir dos tipos:
-> Variable cualitativa nominal: Una variable cualitativa
nominal presenta modalidades no numéricas que no admiten un criterio de
orden. Ejemplo: El estado civil, con las siguientes modalidades: soltero,
casado, separado, divorciado y viudo.
-> Variable cualitativa ordinal o variable cuasicuantitativa:
presenta modalidades no numéricas, en las que existe un orden. Ejemplo:
Medallas de una prueba deportiva: oro, plata, bronce.
Variables Cualitativas

5. Las variables cuantitativas Una variable cuantitativa es la que se expresa mediante
un número, por tanto se pueden realizar operaciones aritméticas con ella. Son
aquellas variables estadísticas que miden de manera numérica y cuantificable el
conjunto de observaciones de la muestra o población
Ejemplos:
Estatura de varones adultos.
Podemos distinguir dos tipos:
-> Variable cuantitativa discreta: Una variable discreta es aquella que
toma valores aislados, es decir no admite valores intermedios entre dos valores
específicos. Por ejemplo:
El número de hermanos de 5 amigos: 2, 1, 0, 1, 3.
-> Variable cuantitativa continua: Una variable continua es aquella que puede
tomar valores comprendidos entre dos números. Por ejemplo:
La altura de los 5 amigos: 1.73, 1.82, 1.77, 1.69, 1.75.
Variables Cuantitativas

6. Definición de Población
Hace referencia al “universo” o “colectivo” de
referencia sobre el que se hacen las observaciones,
la “n” de la distribución. Aunque en demografía se
use prolijamente el instrumental estadístico, este
uso del término tampoco hace referencia al objeto
de la disciplina demográfica.
Ejemplos de poblacion:
es fácil de ejemplificar en una frase como “al
empezar el siglo XX la humanidad (población=
objeto del análisis) había superado ya los 1000
millones de personas (población= estoc o
volumen alcanzado en un determinado
instante).

7. Definición de Muestra
una muestra es un subconjunto de casos o individuos de una
población estadística.
Las muestras se obtienen con la intención de inferir propiedades
de la totalidad de la población, para lo cual deben ser
representativas de la misma. Para cumplir esta característica la
inclusión de sujetos en la muestra debe seguir una técnica de
muestreo. En tales casos, puede obtenerse una información
similar a la de un estudio exhaustivo con mayor rapidez y menor
coste.
Ejemplos de muestra:
1) se desea realizar un estudio acerca de la estructura por edades de los
habitantes de una ciudad.
característica principal en estudio: la edad.
Universo: Todos los habitantes de la ciudad.
Población: Todas las edades individuales de cada uno de los habitantes de la
ciudad.
muestra: las edades correspondientes a los habitantes de un barrio o sector de la
ciudad.

8. Parámetro Estadístico
Un parámetro estadístico es aquel formado por una función
establecida sobre los valores numéricos de una comunidad. Se
trata, por lo tanto, de una cifra representativa que permite
modelizar un plano real.
un parámetro es un número que resume la gran cantidad de datos
que pueden derivarse del estudio de una variable estadística. El
cálculo de este número está bien definido, usualmente mediante
una fórmula aritmética obtenida a partir de datos de la población.
Hay tres tipos parámetros estadísticos:
De centralización.
De posición
De dispersión.

9. Medidas de Centralización
Nos indican en torno a qué valor (centro) se distribuyen los datos.
La medidas de centralización son:
Media aritmética
La media es el valor promedio de la distribución.
Mediana
La mediana es la puntación de la escala que separa la mitad superior de la distribución y la inferior, es decir
divide la serie de datos en dos partes iguales.
Moda
La moda es el valor que más se repite en una distribución.

10. Medidas de Posición
Las medidas de posición dividen un conjunto de datos en grupos con el mismo número de individuos.
Para calcular las medidas de posición es necesario que los datos estén ordenados de menor a mayor.
La medidas de posición son:
Cuartiles
Los cuartiles dividen la serie de datos en cuatro partes iguales.
Deciles
Los deciles dividen la serie de datos en diez partes iguales.
Percentiles
Los percentiles dividen la serie de datos en cien partes iguales.

11. Medidas de Dispersión
Las medidas de dispersión nos informan sobre cuanto se alejan del centro los valores de la distribución.
Las medidas de dispersión son:
Rango o recorrido
El rango es la diferencia entre el mayor y el menor de los datos de una distribución estadística.
Desviación media
La desviación media es la media aritmética de los valores absolutos de las desviaciones respecto a la media.
Varianza
La varianza es la media aritmética del cuadrado de las desviaciones respecto a la media.
Desviación típica
La desviación típica es la raíz cuadrada de la varianza.

12. Escalas de Medición
El proceso de asignar un valor numérico a una variable se llama
medición. Las escalas de medición sirven para ofrecernos
información sobre las clasificaciones que podemos hacer con
respecto a las variables (discretas o continuas).
Cuando se mide una variable el resultado puede aparecer en uno
de cuatro diversos tipos de escalas de medición; nominal, ordinal,
intervalo y razón.
Conocer la escala a la que pertenece una medición es importante
para determinar el método adecuado para describir y analizar
esos datos..
Ejemplo:
Si evaluamos el rendimiento académico de
estudiantes podemos asignar el valor cero al mínimo
rendimiento imaginable al respecto; al mayor
rendimiento posible podemos atribuirle un valor de
100, 20, 10 o 7 puntos, según resulte más práctico.
Con estos dos valores tendríamos ya marcados los
límites de nuestra escala.

13. Tipos de Escalas

14. Escalas de Nominal
es categórica, consiste en designar o nombrar las observaciones.
Las categorías son mutuamentes excluyentes y colectivamente
exhaustivas. No es posible ordenar las categorías.
Son dicotómicas (no ordenables): sano o enfermo, si o no La
práctica de utilizar números para distinguir entre diversos
diagnósticos médicos constituye una medición sobre una escala
nominal.
Ejemplo:
En el análisis de datos resulta más sencillo asignar a ciertos atributos
“etiquetas” numéricas en lugar de utilizar datos complejos. Por ello
podemos utilizar un “1” para designar a las mujeres y un “2” para designar
a los hombres, sin que ninguno de los números represente más o menos,
solamente con el objetivo de distinguir y organizar datos.
En esta escala cada persona u objeto debe pertenecer a una y solamente
una de las categorías que tienen y el conjunto de estas categorías debe
ser exhaustivo; es decir, tiene que contener a todos los casos posibles.

15. Escalas de Ordinal
Es categórica. Cuando las observaciones no sólo difieran de
categoría a categoría, sino que además pueden clasificarse por
grados de acuerdo con algún criterio de orden (Glass y Stanley,
1986).
En esta escala los números representan una clasificación (mayor
que o menor que), sin que represente una unidad de medida,
quedando implícito que un número de mayor cantidad tiene más
alto grado de atributo medido en comparación de un número
menor. Se establece una gradación u orden natural para las
categorías, cada uno de los datos puede localizarse dentro de
alguna de las categorías disponibles.
Ejemplo:
Niveles de una enfermedad. Rango
académico. Edad (menor igual a 18 años;
mayor a 18 años y menor a 40 años; mayor
igual a 40 años)

16. Escalas de Intervalo
Es cuantitativa. No sólo distingue orden entre categorías, sino
que también pueden discernirse diferencias iguales entre las
observaciones.
Refleja distancias equivalentes entre los objetos y en la propia
escala. Es decir, el uso de ésta escala permite indicar exactamente
la separación entre 2 puntos, lo cual, de acuerdo al principio de
isomorfismos, se traduce en la certeza de que los objetos así
medidos están igualmente separados a la distancia o magnitud
expresada en la escala.
Ejemplo:
Se considera unidad de medida, según un parámetro (escalas de
grados en temperatura, metros, pie, puntajes). Cero arbitrario, es
decir, el valor cero no indica ausencia de la característica, en otras
palabras, la característica está presente y vale cero algunos
ejemplos son la temperatura, pruebas de coeficiente intelectual,
académicas, altura sobre el nivel del mar .

17. Escalas de Razón
Es cuantitativa. Cero absoluto, es decir, el valor cero representa
ausencia de la característica o atributo .
Constituye el nivel óptimo de medición, posee un cero verdadero
como origen, también denominada escala de proporciones. La
existencia de un cero, natural y absoluto, significa la posibilidad
de que el objeto estudiado carezca de propiedad medida, además
de permitir todas las operaciones aritméticas y el uso de números
representada cantidades reales de la propiedad medida.
Ejemplo:
Claros ejemplos de esta escala son
la distancia, altura, masa, peso,
estatura, entre otros.

18. Sumatoria: también conocido como operación de
suma o notación sigma, es un operador matemático que permite
representar sumas de muchos sumandos, n o incluso infinitos
sumandos. Se expresa con la letra griega sigma ( , Σ), y se define
como:
Razón:La Razón es el cociente entre dos
números, en el que ninguno o sólo algunos
elementos del numerador están incluidos en el
denominador. El rango es de 0 a infinito.
Ejemplos:Suponga que el peso de cuatro piezas fundidas de
metal son 2.0, 2.1, 2.3 y 2.5 kg. El orden(ordinal) y la diferencia
(intervalo) en los pesos puede ser comparado. Así, el
incremento de peso de 2.0 a 2.1 es de 0.1 kg, el cual es el
mismo que el que existe entre 2.3 y 2.4 kg. Tambien, cuando
comparamos los pesos de 2.0 a 2.4 kg, se encuentra una razón
significativa: el peso de una pieza de metal de 2.4 kg es un 20%
más pesada que una que pese 2.0 kg. Existe un cero natural o
real para la escala, así 0kg implica no peso.

19. TASA
La tasa mide la magnitud de cambio de un parámetro por unidad de cambio de otro. Es un
tipo especial de razón o de proporción que incluye una medida de tiempo en el
denominador
En las tasas usadas en epidemiología, la magnitud Y del numerador es el número de sujetos
con una determinada característica y la magnitud X del denominador es el tiempo.
Por tanto, la Tasa es una medida de cambio que permite pedir el “ritmo” de aparición de un
evento
Al ser difícil el cálculo de la “tasa instantánea”, normalmente se habla de “tasa media”.
Frecuencia es la cantidad de veces que se repite un
suceso en un rango de un espacio muestral dado.
Por ejemplo, una profesora en su informe anual,
señalará que para el curso de 35 alumnos, la
frecuencia de notas es la siguiente.
Proporción es una igualdad entre dos razones , y aparece
frecuentemente en notación fraccionaria.Por ejemplo:
2 = 6
5 15
Para resolver una proporción, debemos multiplicar cruzado para
formar una ecuación. Por ejemplo: 2/5 = 6/5 =
152 · 15 = 6 · 530 = 30

20. Bibliografía
http://www.ditutor.com/estadistica/estadistica.html.
http://estadisticaparaadministracion.blogspot.com/2012/05/de-los-
datos-variables-cualitativa.html.
http://dv.ujaen.es/docencia/ilias.php?ref_id=85771&from_page=270
98&obj_id=33271&cmd=layout&cmdClass=illmpresentationgui&cmd
Node=9i&baseClass=ilLMPresentationGUI
http://www.educarchile.cl/ech/pro/app/detalle?ID=141885
http://www.vitutor.com/estadistica/descriptiva/a_7.html
https://es.wikipedia.org/wiki/Parámetro_estadístico
sameens.dia.uned.es/Trabajos6/Trabajos_Publicos/Trab.../Razon.htm