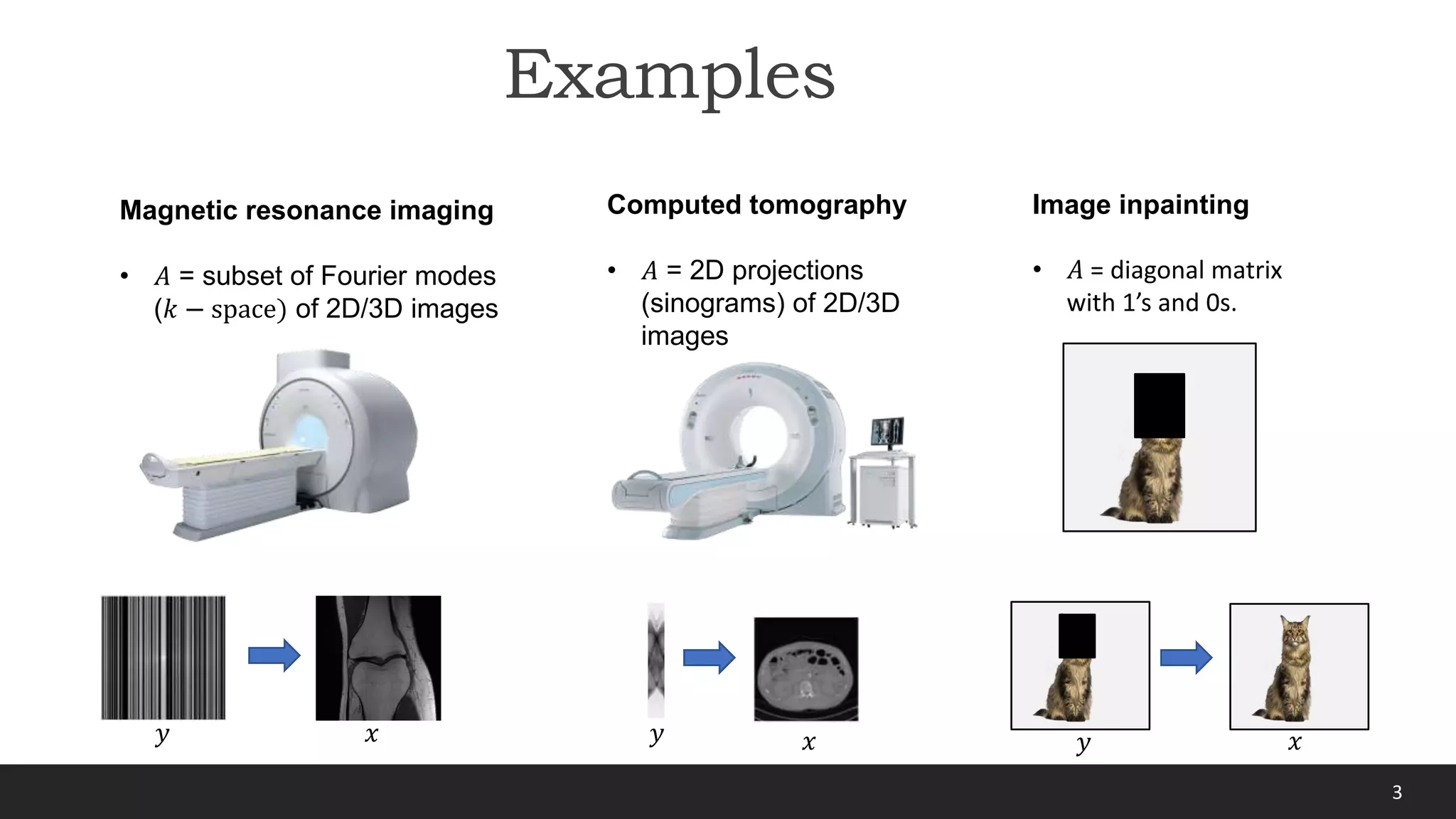
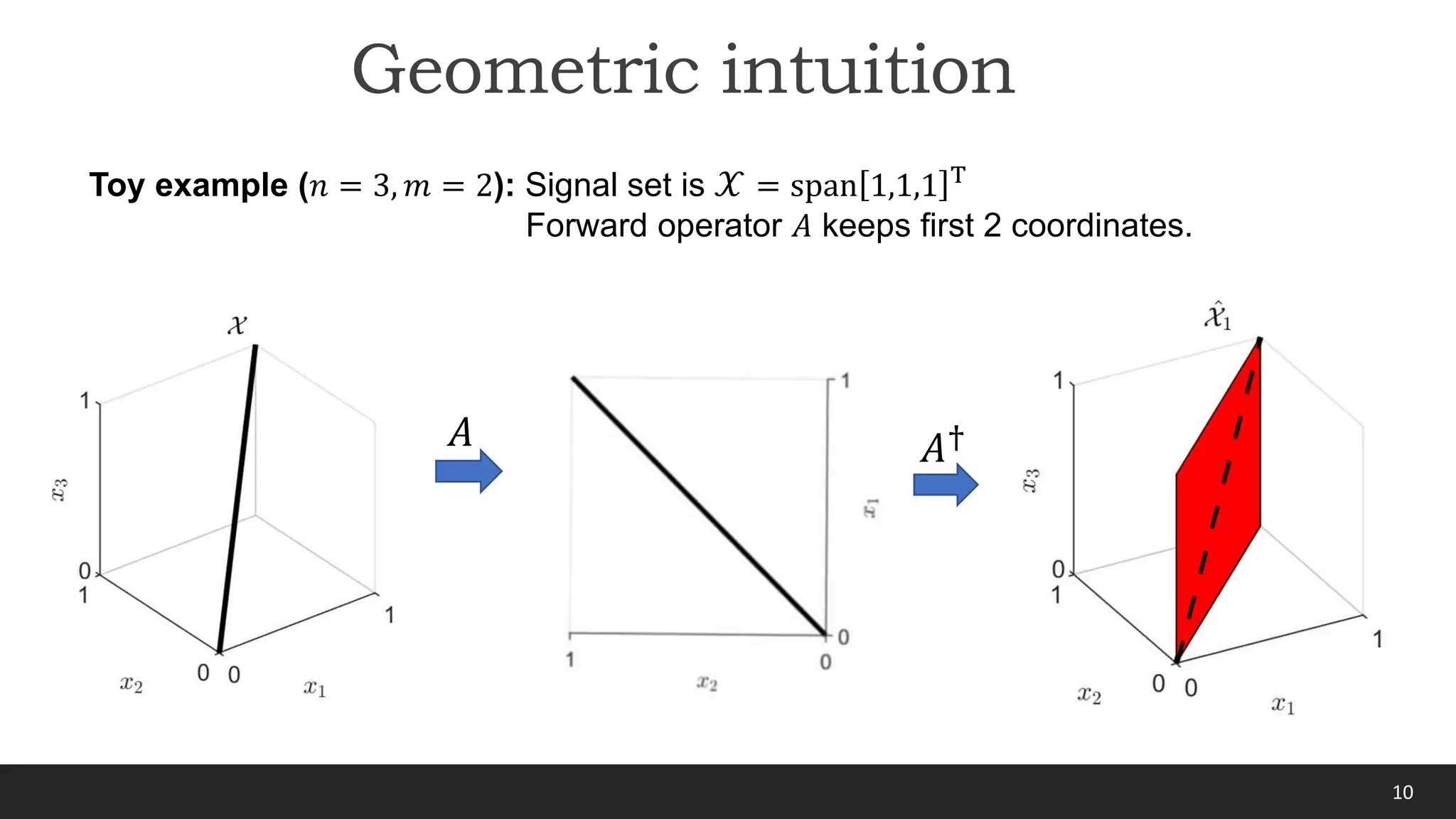
1) The document discusses equivariant imaging, a method for learning to solve inverse problems from measurements alone without ground truth data.
2) It introduces the concept of exploiting symmetries in natural signals to learn the inversion function from multiple related measurement operators.
3) A key innovation is an unsupervised loss function that enforces the learned inversion to be equivariant to the underlying signal symmetries, allowing training from noisy measurements without clean signals.





![7
Advantages:
• State-of-the-art reconstructions
• Once trained, 𝒇 is easy to evaluate
Learning approach
x8 accelerated MRI [Zbontar et al., 2019]
Deep network
(34.5 dB)
Ground-truth
Total variation
(28.2 dB)](https://image.slidesharecdn.com/enslcolloquium-220224220243/75/Equivariant-Imaging-7-2048.jpg)














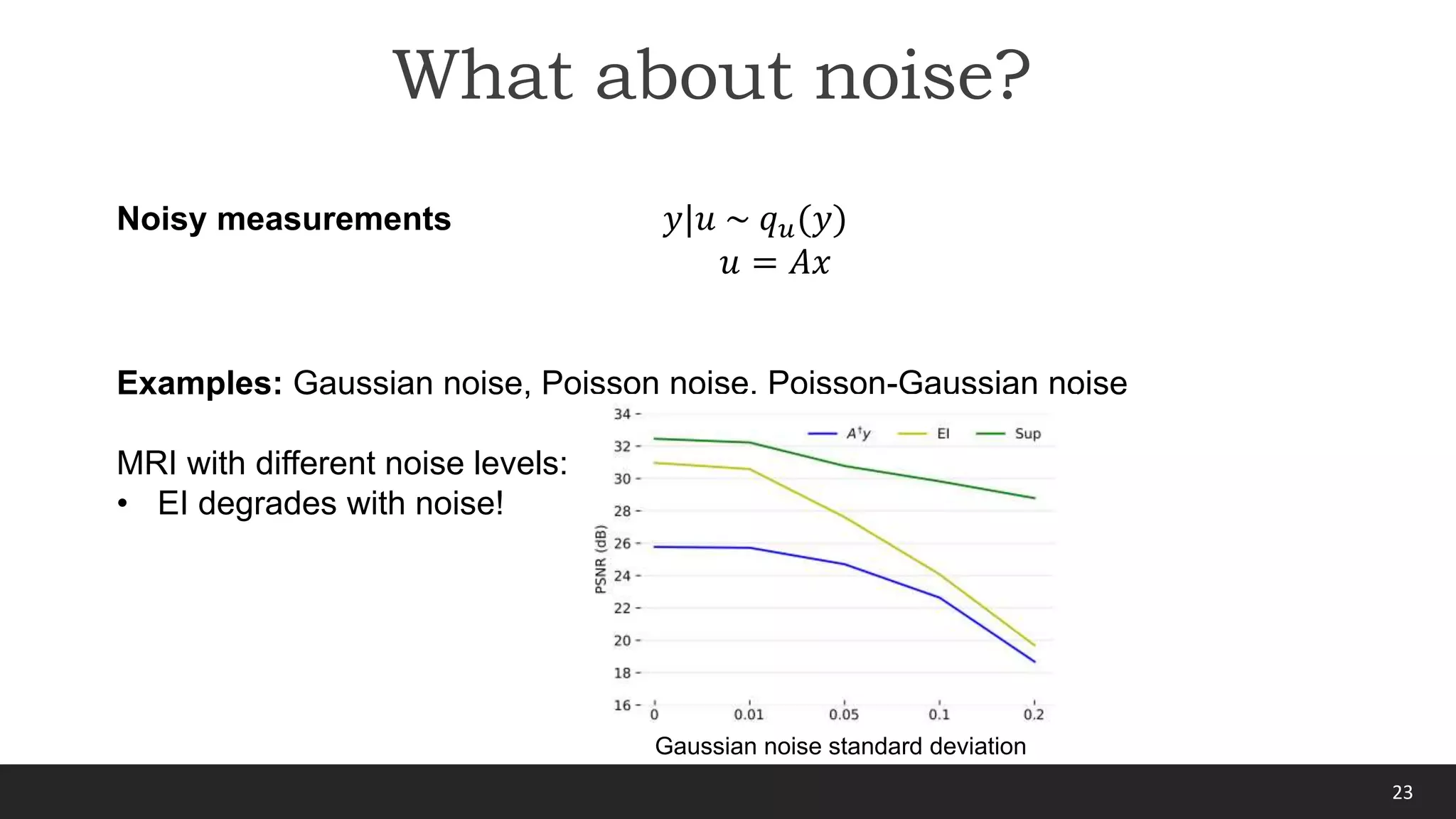

![25
Gaussian noise 𝑦 ∼ 𝒩(𝑢, 𝐼𝜎2)
ℒ𝑆𝑈𝑅𝐸 𝑓 =
𝑖
𝑦𝑖 − 𝐴𝑓 𝑦𝑖
2
− 𝜎2𝑚 + 2𝜎2div(𝐴 ∘ 𝑓)(𝑦𝑖)
where div ℎ(𝑥) = 𝑗
𝛿ℎ𝑗
𝛿𝑥𝑗
is approximated with a Monte Carlo estimate which only
requires evaluations of ℎ [Ramani, 2008]
Theorem [Stein, 1981] Under mild differentiability conditions on the function 𝐴 ∘ 𝑓,
the following holds
Handling noise via SURE
𝔼𝑦,𝑢 ℒ𝑀𝐶 𝑓 = 𝔼𝑦 ℒ𝑆𝑈𝑅𝐸 𝑓](https://image.slidesharecdn.com/enslcolloquium-220224220243/75/Equivariant-Imaging-25-2048.jpg)








![34
Papers
[1] “Equivariant Imaging: Learning Beyond the Range Space” (2021), Chen, Tachella and Davies, ICCV 2021
[2] “Robust Equivariant Imaging: a fully unsupervised framework for learning to image from noisy and partial
measurements” (2021), Chen, Tachella and Davies, Arxiv
[3] “Sampling Theorems for Unsupervised Learning in Inverse Problems” (2022), Tachella, Chen and Davies, to appear.](https://image.slidesharecdn.com/enslcolloquium-220224220243/75/Equivariant-Imaging-34-2048.jpg)
