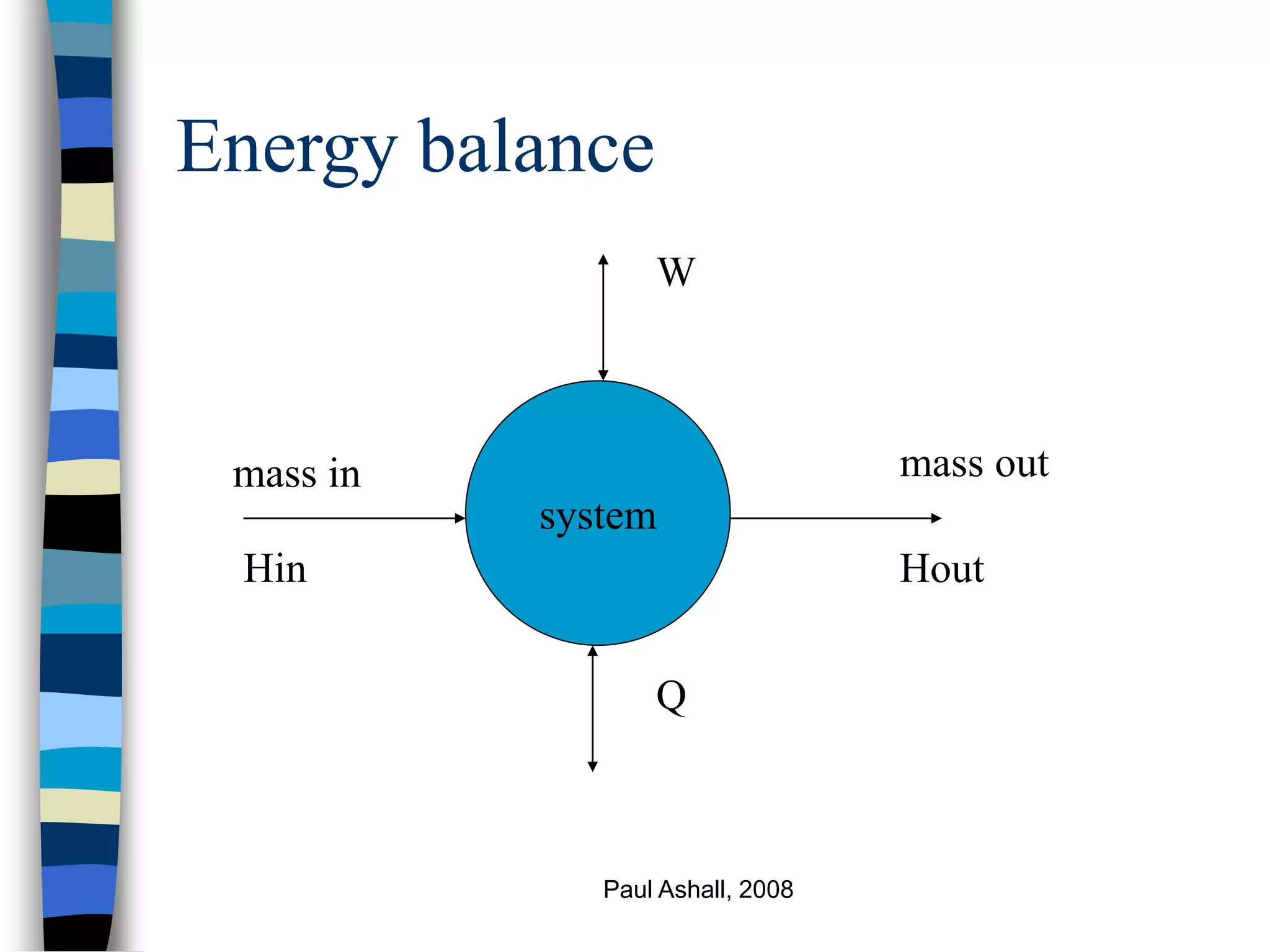
This document discusses energy balances and their application in chemical processes. It covers the first law of thermodynamics, forms of energy, and the conventions used in energy balances. Equations for enthalpy, mechanical energy, and heat capacity are presented. Methods are described for performing energy balances on systems involving phase changes, chemical reactions, and other processes. Key data sources for thermochemical properties are also listed.

1. Paul Ashall, 2008
Module 9001
Energy Balance
Paul Ashall, 2008

2. Paul Ashall, 2008
 Concerned with energy changes and
energy flow in a chemical process.
 Conservation of energy – first law of
thermodynamics i.e. accumulation of
energy in a system = energy input –
energy output

3. Paul Ashall, 2008
Forms of energy
 Potential energy (mgh)
 Kinetic energy (1/2 mv2)
 Thermal energy – heat (Q) supplied to or removed
from a process
 Work energy – e.g. work done by a pump (W) to
transport fluids
 Internal energy (U) of molecules
m – mass (kg)
g – gravitational constant, 9.81 ms-2
v – velocity, ms-1

4. Paul Ashall, 2008
Energy balance
system
mass in
Hin
mass out
Hout
W
Q

5. Paul Ashall, 2008
IUPAC convention
- heat transferred to a system is +ve and
heat transferred from a system is –ve
- work done on a system is+ve and work
done by a system is -ve

6. Paul Ashall, 2008
Steady state/non-steady state
 Non steady state -
accumulation/depletion of energy in
system

7. Paul Ashall, 2008
Uses
 Heat required for a process
 Rate of heat removal from a process
 Heat transfer/design of heat exchangers
 Process design to determine energy
requirements of a process
 Pump power requirements (mechanical
energy balance)
 Pattern of energy usage in operation
 Process control
 Process design & development
 etc

8. Paul Ashall, 2008
Enthalpy balance
 p.e., k.e., W terms = 0
 Q = H2 – H1 or Q = ΔH
, where H2 is the total enthalpy of output
streams and H1is the total enthalpy of
input streams, Q is the difference in
total enthalpy i.e. the enthalpy (heat)
transferred to or from the system

9. Paul Ashall, 2008
continued
 Q –ve (H1>H2), heat removed from
system
 Q +ve (H2>H1), heat supplied to
system.

10. Paul Ashall, 2008
Example – steam boiler
Two input streams: stream 1- 120 kg/min.
water, 30 deg cent., H = 125.7 kJ/kg;
stream 2 – 175 kg/min, 65 deg cent, H=
272 kJ/kg
One output stream: 295 kg/min. saturated
steam(17 atm., 204 deg cent.), H =
2793.4 kJ/kg

11. Paul Ashall, 2008
continued
Ignore k.e. and p.e. terms relative to enthalpy
changes for processes involving phase
changes, chemical reactions, large
temperature changes etc
Q = ΔH (enthalpy balance)
Basis for calculation 1 min.
Steady state
Q = Hout – Hin
Q = [295 x 2793.4] – [(120 x 125.7) + (175 x 272)]
Q = + 7.67 x 105 kJ/min

12. Paul Ashall, 2008
Steam tables
 Enthalpy values (H kJ/kg) at various P,
T

13. Paul Ashall, 2008
Enthalpy changes
 Change of T at constant P
 Change of P at constant T
 Change of phase
 Solution
 Mixing
 Chemical reaction
 crystallisation

14. Paul Ashall, 2008
Latent heats (phase changes)
 Vapourisation (L to V)
 Melting (S to L)
 Sublimation (S to V)

15. Paul Ashall, 2008
Mechanical energy balance
 Consider mechanical energy terms only
 Application to flow of liquids
ΔP + Δ v2 + g Δh +F = W
ρ 2
where W is work done on system by a pump
and F is frictional energy loss in system (J/kg)
ΔP = P2 – P1; Δ v2 = v2
2 –v1
2; Δh = h2 –h1
 Bernoulli equation (F=0, W=0)

16. Paul Ashall, 2008
Example - Bernoulli eqtn.
Water flows between two points 1,2. The
volumetric flow rate is 20 litres/min.
Point 2 is 50 m higher than point 1. The
pipe internal diameters are 0.5 cm at
point 1 and 1 cm at point 2. The
pressure at point 2 is 1 atm..
Calculate the pressure at point 2.

17. Paul Ashall, 2008
continued
ΔP/ρ + Δv2/2 + gΔh +F = W
ΔP = P2 – P1 (Pa)
Δv2 = v2
2 – v1
2
Δh = h2 - h1 (m)
F= frictional energy loss (mechanical energy
loss to system) (J/kg)
W = work done on system by pump (J/kg)
ρ = 1000 kg/m3

18. Paul Ashall, 2008
continued
Volumetric flow is 20/(1000.60) m3/s
= 0.000333 m3/s
v1 = 0.000333/(π(0.0025)2) = 16.97 m/s
v2 = 0.000333/ (π(0.005)2) = 4.24 m/s
(101325 - P1)/1000 + [(4.24)2 – (16.97)2]/2 + 9.81.50 = 0
P1 = 456825 Pa (4.6 bar)

19. Paul Ashall, 2008
Sensible heat/enthalpy
calculations
 ‘Sensible’ heat – heat/enthalpy that must be
transferred to raise or lower the temperature of a
substance or mixture of substances.
 Heat capacities/specific heats (solids, liquids,
gases,vapours)
 Heat capacity/specific heat at constant P, Cp(T) =
dH/dT or ΔH = integral Cp(T)dT between limits T2 and
T1
 Use of mean heat capacities/specific heats over a
temperature range
 Use of simple empirical equations to describe the
variation of Cp with T

20. Paul Ashall, 2008
continued
e.g. Cp = a + bT + cT2 + dT3
,where a, b, c, d are coefficients
ΔH = integralCpdT between limits T2, T1
ΔH = [aT + bT2 + cT3 + dT4]
2 3 4
Calculate values for T = T2, T1 and subtract
Note: T may be in deg cent or K - check units for Cp!

21. Paul Ashall, 2008
Example
Calculate the enthalpy required to heat a
stream of nitrogen gas flowing at 100
mole/min., through a gas heater from 20
to 100 deg. cent.
(use mean Cp value 29.1J mol-1 K-1 or Cp
= 29 + 0.22 x 10-2T + 0.572 x 10-5T2 –
2.87 x 10-9 T3, where T is in deg cent)

22. Paul Ashall, 2008
Heat capacity/specific heat data
 Felder & Rousseau pp372/373 and Table B10
 Perry’s Chemical Engineers Handbook
 The properties of gases and liquids, R. Reid et al, 4th
edition, McGraw Hill, 1987
 Estimating thermochemical properties of liquids part
7- heat capacity, P. Gold & G.Ogle, Chem. Eng.,
1969, p130
 Coulson & Richardson Chem. Eng., Vol. 6, 3rd
edition, ch. 8, pp321-324
 ‘PhysProps’

23. Paul Ashall, 2008
Example – change of phase
A feed stream to a distillation unit contains an equimolar
mixture of benzene and toluene at 10 deg cent.The
vapour stream from the top of the column contains
68.4 mol % benzene at 50 deg cent. and the liquid
stream from the bottom of the column contains 40
mol% benzene at 50 deg cent.
[Need Cp (benzene, liquid), Cp (toluene, liquid), Cp
(benzene, vapour), Cp (toluene, vapour), latent heat
of vapourisation benzene, latent heat of vapourisation
toluene.]

24. Paul Ashall, 2008
Energy balances on systems
involving chemical reaction
 Standard heat of formation (ΔHo
f) – heat of
reaction when product is formed from its
elements in their standard states at 298 K, 1
atm. (kJ/mol)
aA + bB cC + dD
-a -b +c +d (stoichiometric
coefficients, νi)
ΔHo
fA, ΔHo
fB, ΔHo
fC, ΔHo
fD (heats of formation)
ΔHo
R = c ΔHo
fC + d ΔHo
fD - a ΔHo
fA - bΔHo
fB

25. Paul Ashall, 2008
Heat (enthalpy) of reaction
 ΔHo
R –ve (exothermic reaction)
 ΔHo
R +ve (endothermic reaction)

26. Paul Ashall, 2008
Enthalpy balance equation -
reactor
Qp = Hproducts – Hreactants + Qr
Qp – heat transferred to or from process
Qr – reaction heat (ζ ΔHo
R), where ζ is
extent of reaction and is equal to [moles
component,i, out – moles component i,
in]/ νi

27. Paul Ashall, 2008
system
Qr
Hreactants
Hproducts
Qp
+ve
-ve
Note: enthalpy values must be calculated with reference to a
temperature of 25 deg cent

28. Paul Ashall, 2008
Energy balance techniques
 Complete mass balance/molar balance
 Calculate all enthalpy changes between
process conditions and standard/reference
conditions for all components at start (input)
and finish (output).
 Consider any additional enthalpy changes
 Solve enthalpy balance equation

29. Paul Ashall, 2008
Energy balance techniques
 Adiabatic temperature: Qp = 0

30. Paul Ashall, 2008
Examples
 Reactor
 Crystalliser
 Drier
 Distillation

31. Paul Ashall, 2008
References
 The Properties of Gases and Liquids, R.
Reid
 Elementary Principles of Chemical
Processes, R.M.Felder and
R.W.Rousseau