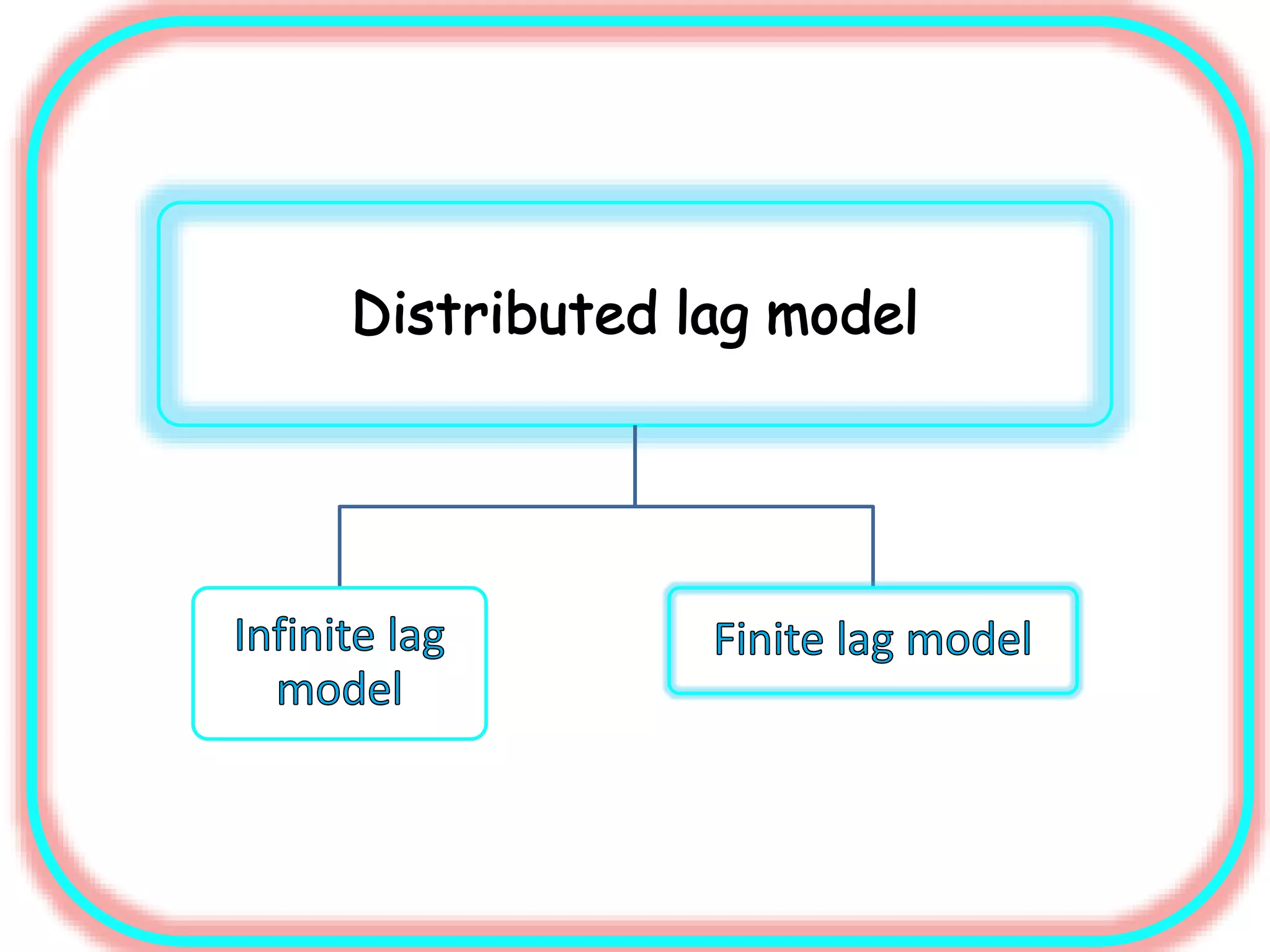
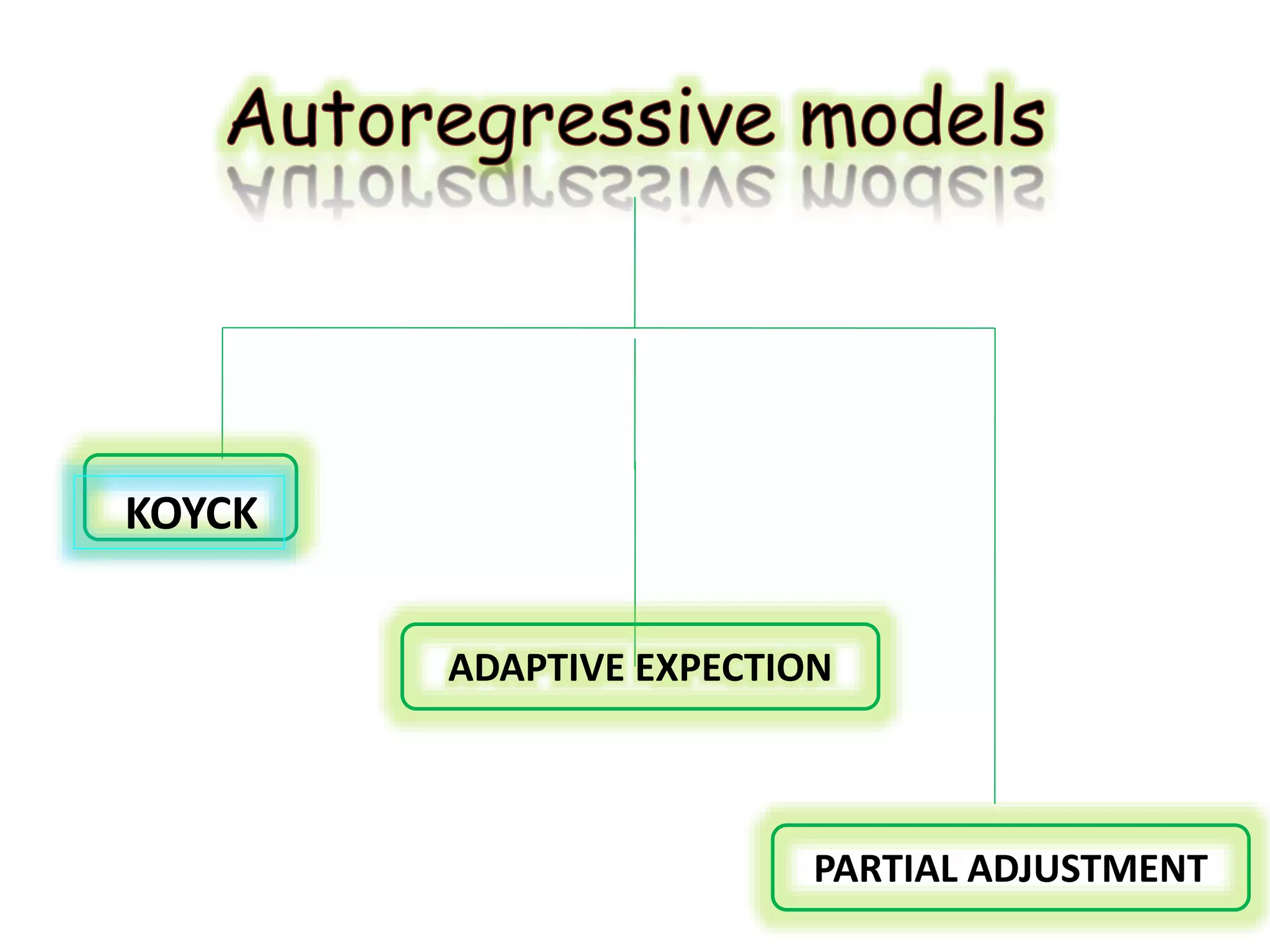
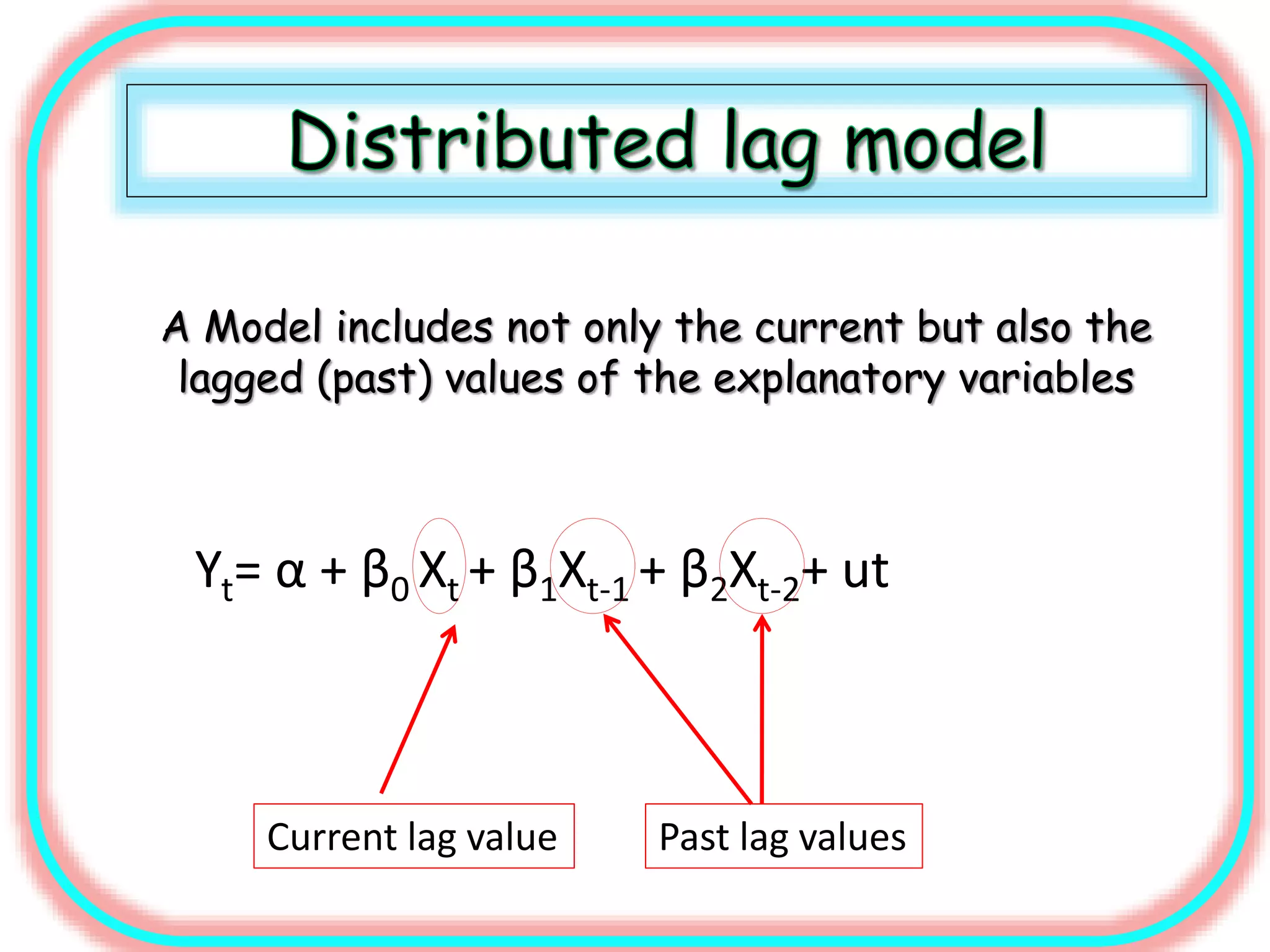
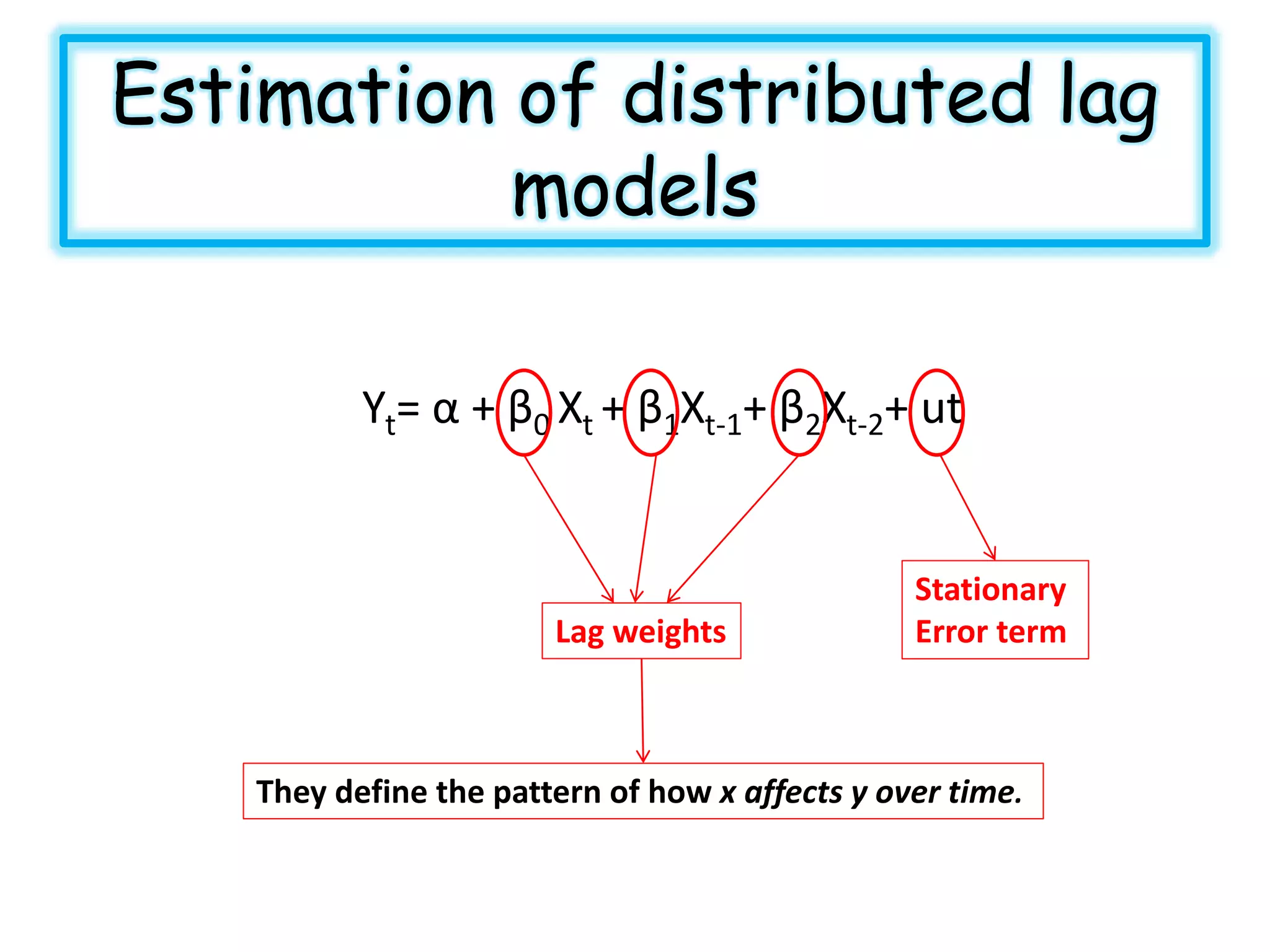
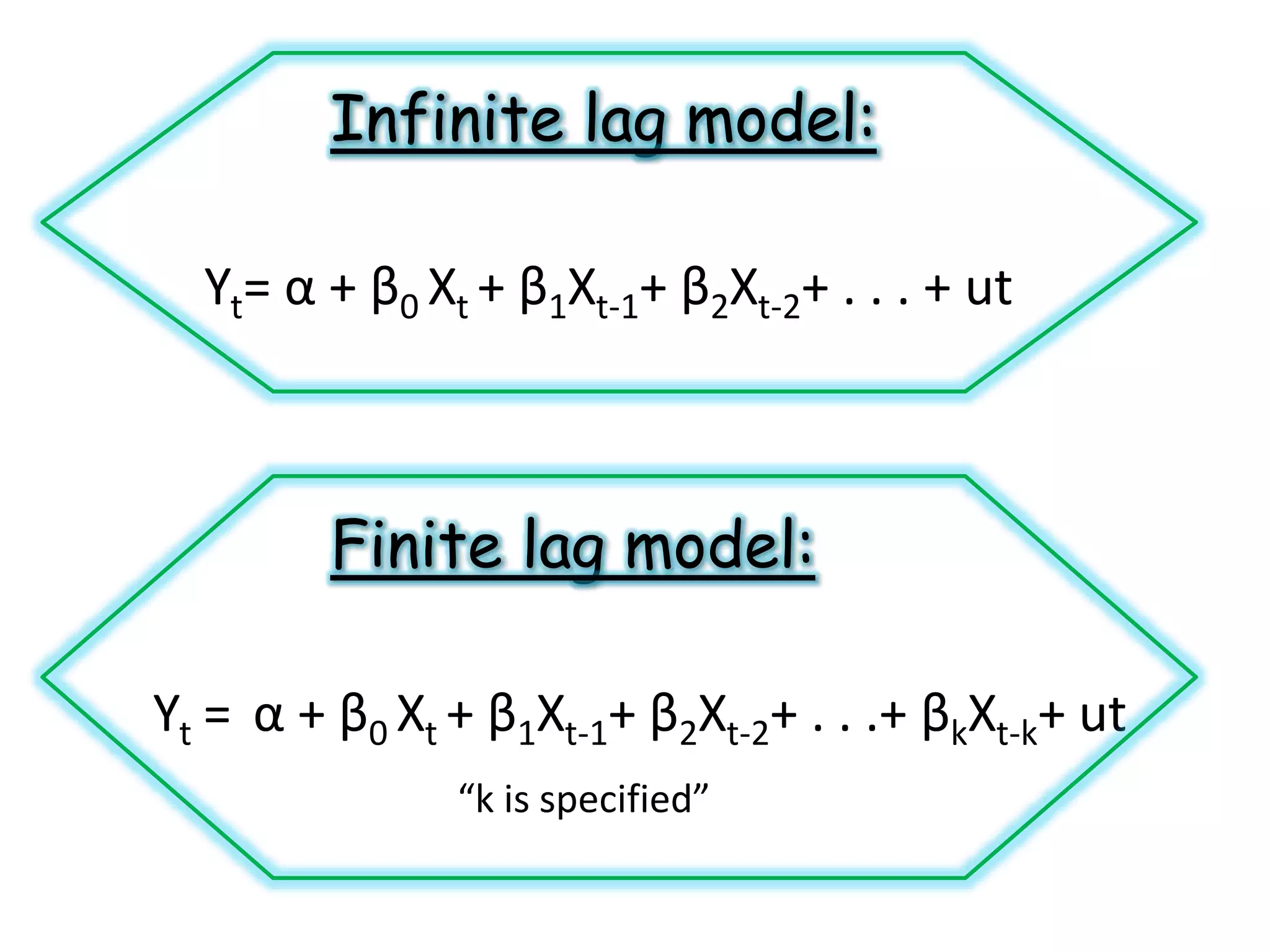
The document discusses the role of lags in economic models. Lags refer to past values of variables that are used to predict current or future values. Models with lags are used to capture delayed effects, where a change in one variable impacts another variable after some time. Specifically, the document discusses: 1) Distributed lag models which include current and past lagged values of explanatory variables to predict a dependent variable. 2) Models with lagged dependent variables to capture partial adjustment effects, where changes in a variable adjust gradually over time rather than immediately. 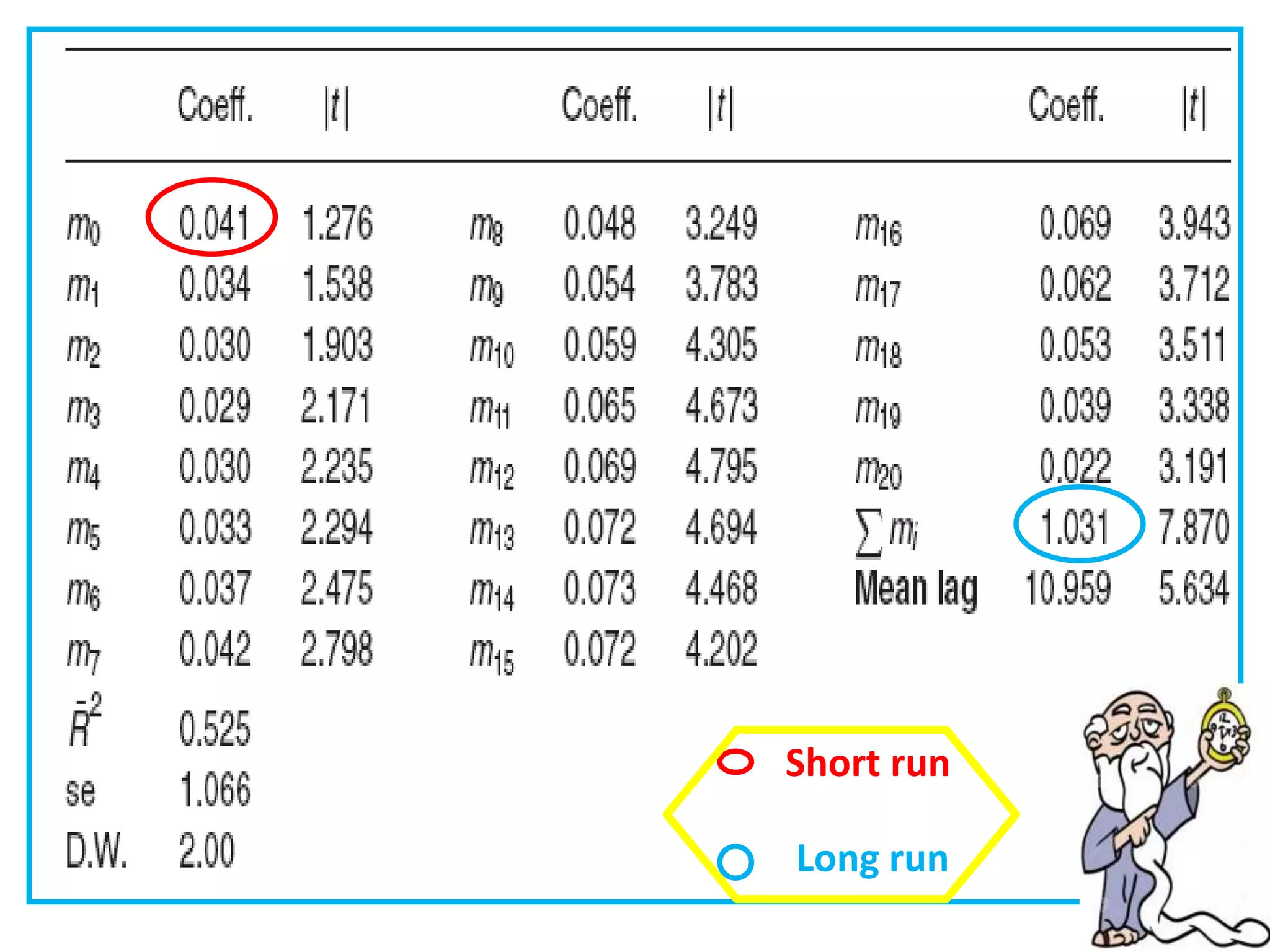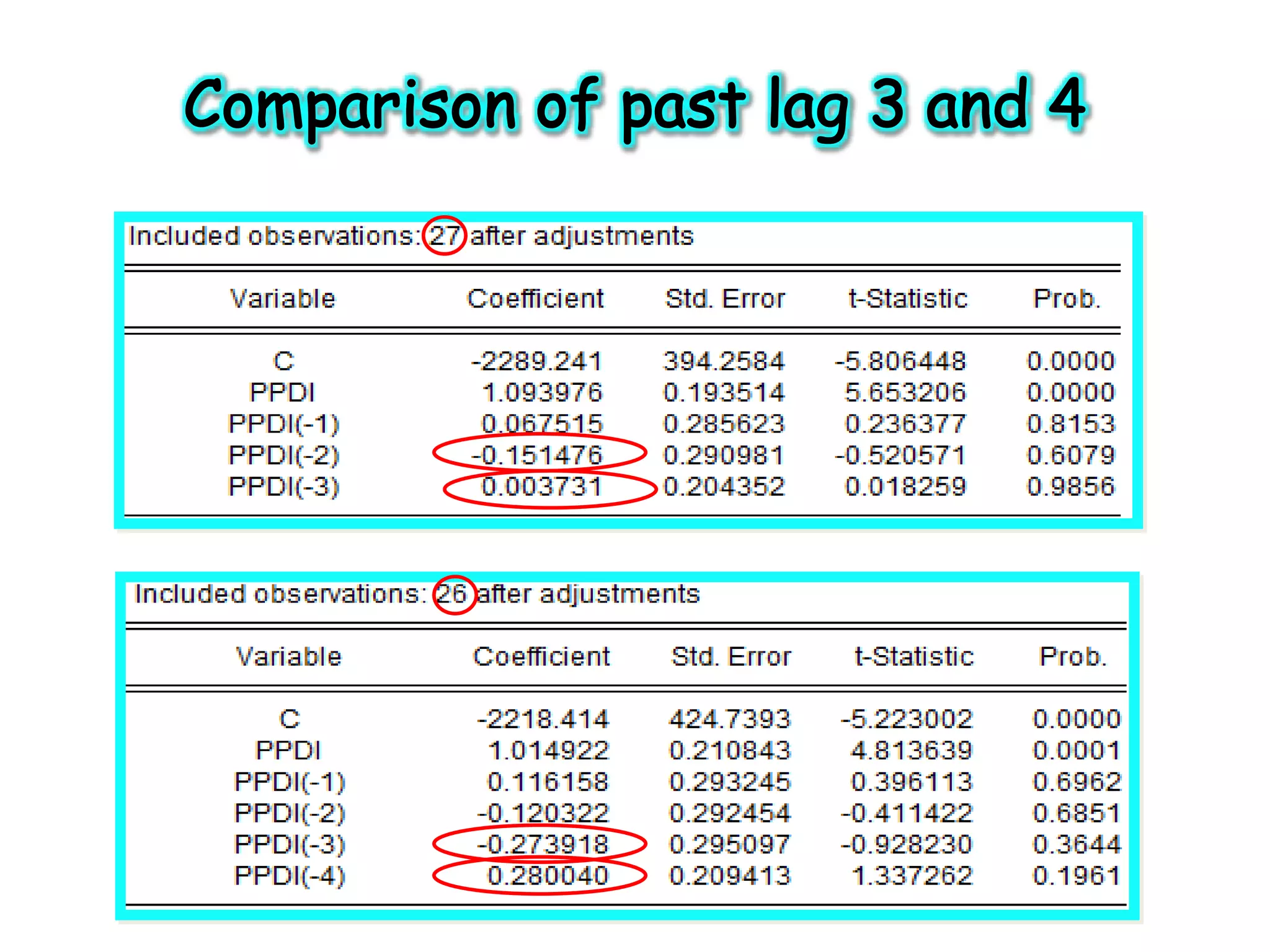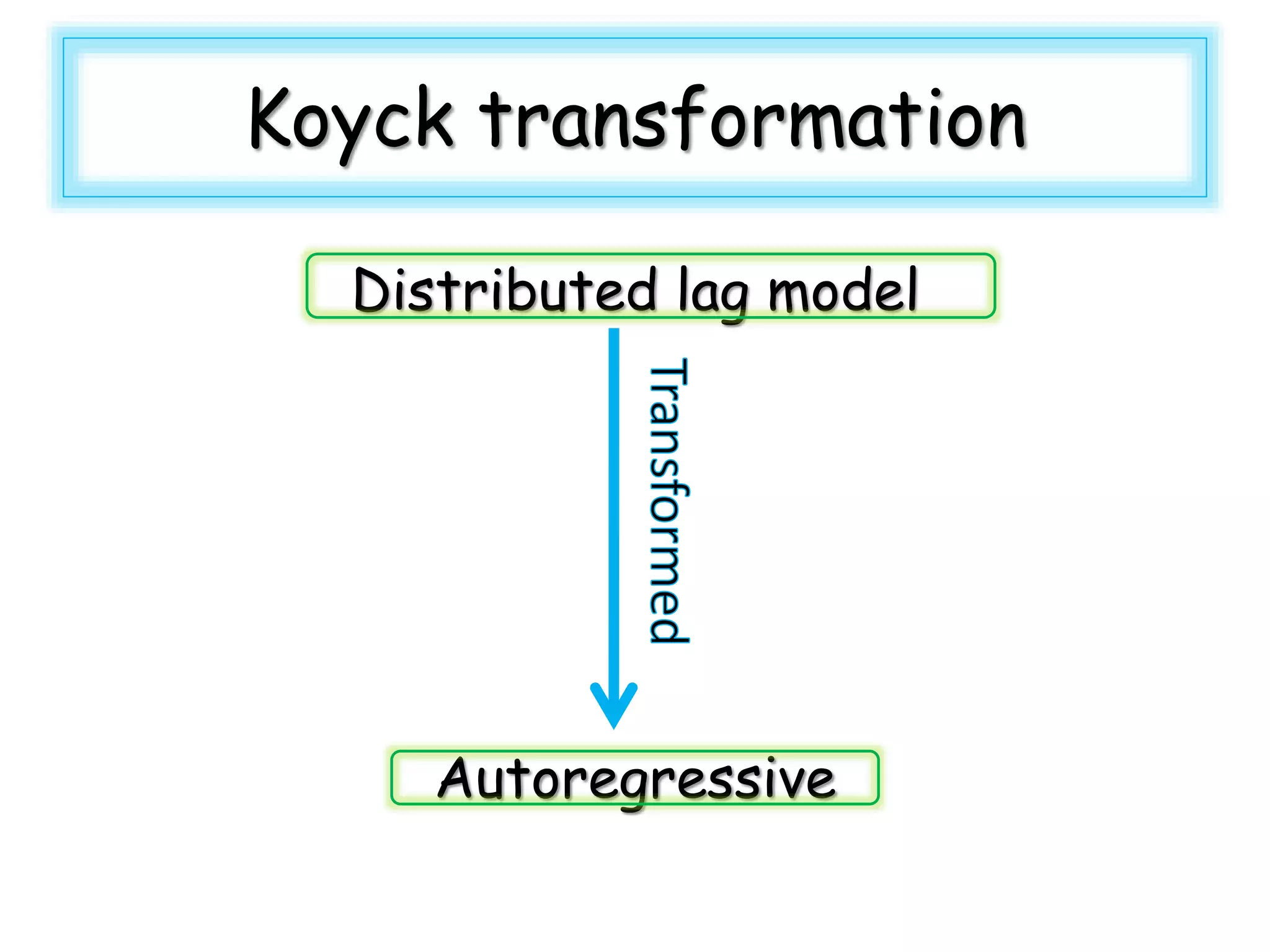3) The Koyck transformation allows estimating the long run impact of a variable from the lag structure in these partial adjustment models. Lags are widely used

2. Two sided Relationship

6. A Model includes not only the current but also the
lagged (past) values of the explanatory variables
Past lag valuesCurrent lag value
Yt= α + β0 Xt + β1Xt-1 + β2Xt-2+ ut

7. The model which includes one or more lagged values of
the dependent variable among its
explanatory variables
Lagged value ofDependent variable
Yt = α + βXt + λ Yt-1 + u

8. What are the role of lags in
Economics

11. Yt = constant + 0.4Xt +0.3Xt-1+0.2Xt-2
Result

12. SHORT RUN
Yt = constant + 0.4Xt +0.3Xt-1+0.2Xt-2
The consumption of Current year of increment

13. LONG RUN
Yt = constant + 0.4Xt +0.3Xt-1+0.2Xt-2
0.9
Sum of the consumption of over all period

14. LINK B/W MONEY AND PRICE

15. Short run
Long run

16. Lag b/w R&D Expenditure And
Productivity

17. Economists have used two rather different styles of research
in their attempts
• To assess the contribution of research and development
(R&D) expenditures.
• For economic growth

18. Paul R. Krugman
(Princeton University)
By
Maurice Obstfeld
(University of California, Berkeley)
B Marc J. Melitz
(Harvard University)

19. The J curve shows the effect of a devaluation of a currency on the net
export (exports minus imports). When the devaluation takes place
at t the net export falls from A to B, since the level of import is
unchanged, but the currency is worth less. As time goes on the net
export will gradually change since consumers buy less imported
goods, and other countries buy more goods from the country due
to the lower real price. At C the net export break even. With time
the net export will find equilibrium

23. Technological reasons

24. Old Computers

25. Alternate of computers: laptop

26. Institutional reasons
1 3 7
Years

27. Estimation of distributed lag
models
Yt= α + β0 Xt + β1Xt-1+ β2Xt-2+ ut
Lag weights
They define the pattern of how x affects y over time.
Stationary
Error term

29. Infinite lag model:
Yt= α + β0 Xt + β1Xt-1+ β2Xt-2+ . . . + ut
Finite lag model:
Yt = α + β0 Xt + β1Xt-1+ β2Xt-2+ . . .+ βkXt-k+ ut
“k is specified”

31. *
*
Since we are using the 1 past lag value so number of observation reduced from 30 to 29
No +ve autocorrelation

33. Interpretation summary
 Short run 1.142786 or a unit change in PPDI on average the PPCE will
increase up to 1.142 units
 Long run 1.142786+(-0.144730)0.99805
 Durbin Watson  no positive autocorrelation
 Observation 1 past lag value include so observation reduce from 30 to 29.
 R square define up to 99.08% effect of PPDI on PPCE.
 % of a total impact of a unit change in PPDI on PPCE :
1st year:1.1427/0.99805 11.4%
2nd year:0.14473/0.998011.44%

39. • Maximum length of the lags.
• Fewer degree of freedom left
• Data mining (big data)
• Multicolinearity

40. Koyck approach
Adjustment of speed
slow 01
β0= βk λk
(k=0,1…)(0<λ<1)
(The higher the value of λ the
lower the speed of adjustment,
and the lower the value of λ the
greater the speed of adjustment)
fast
0.0

41. Koyck transformation
Distributed lag model
Autoregressive

42. 1) Yt = α+ β0 Xt + βo λ Xt-1+ βo λ Xt-2+ . . . +ut (For Infinite lag)
Koyck lag by one period :
2) Yt-1 = α+ β0 Xt-1+ β0 λ Xt-2+ β0 λ2 Xt-3 . . . +ut-1
Multiply by λ :
3) λ Yt-1 = λ α+ λ β0 Xt-1+ β0 λ2 Xt-2+ β0 λ3 Xt-3 . . . +ut-1
Subtracting the 1st and 3rd equation :
Yt = α(1 − λ) + β0 Xt + λYt−1 + vt
We get koyck transformed equation

44. ADAPTIVE EXPECTION
PARTIAL ADJUSTMENT
KOYCK

47. Yt = α(1 − λ) + β0 Xt + λYt−1 + vt
PPCEt = -1242.169 + 0.6033PPDIt + 0.4106PCEt−1 + vt
Rate of adjustment  1 - λ  1- 0.4106
RATE of adjustment  0.589
 Short run : current year consumption of increment
Short run  0.6033
 Long run:
Long run = coeff αt-1 /1- λ  1.0237

48. Yt = α (1 − λ) + β0 Xt + λ Yt−1 + vt
PPCEt = -1242.169 + 0.6033PPDIt + 0.4106PCEt−1 + vt
Median lag: median lag(time required) for 1st half
 Median lag = log(2)/log λ  log(2)/log (0.4106)  0.776
(on average with a unit change in income the median lag(time required) for 1st half is 0.776)
Mean lag: effect of change in in dependent to be felt on dependent variable
 Mean lag = λ /1- λ  0.4106/0.5894  0.6966
(on average ,for the effect of change in ppdi to be felt on ppce)

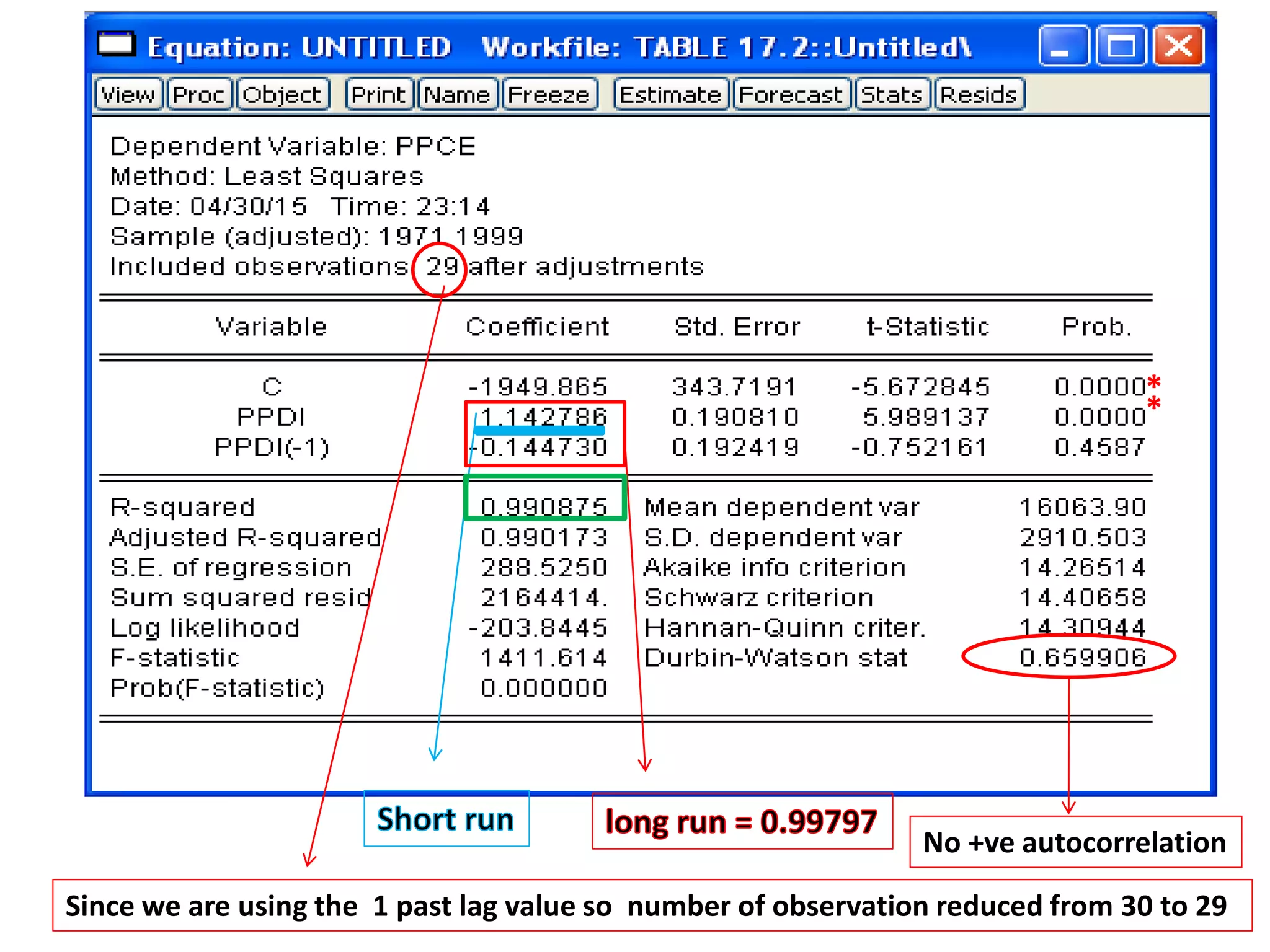
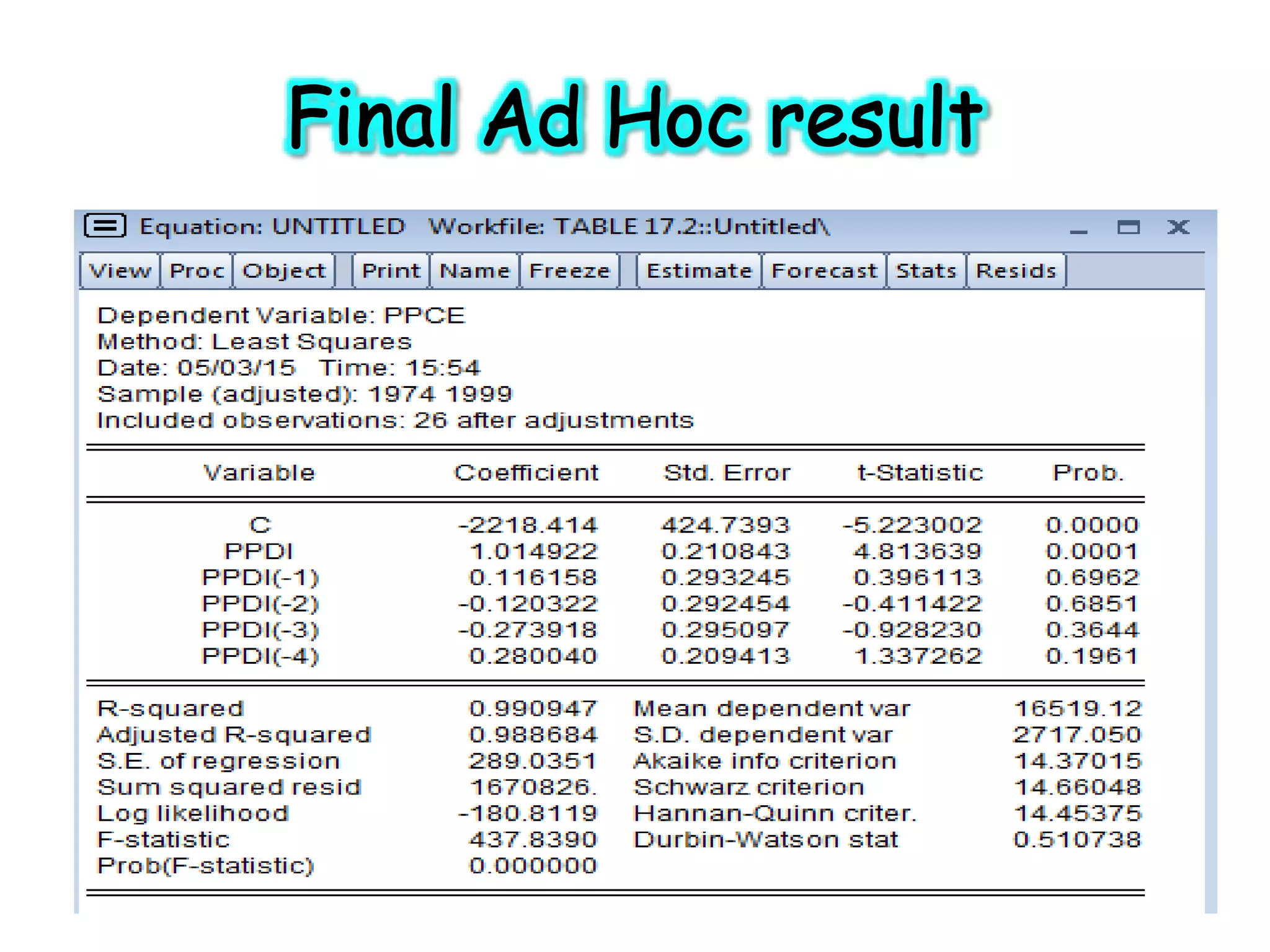
49.  Durbin h test  (1-d/2)[n/1-n{var(αt-1 )} ]1/2
Durbin h test  (0.4972) [(30/1-30(0.239) ]1/2
Durbin h test  5.1191
( Durbin h ~ Norm distribution , As h value exceed ±3 , so the probability is highly significant
Decision:
There is a positive autocorrelation ,
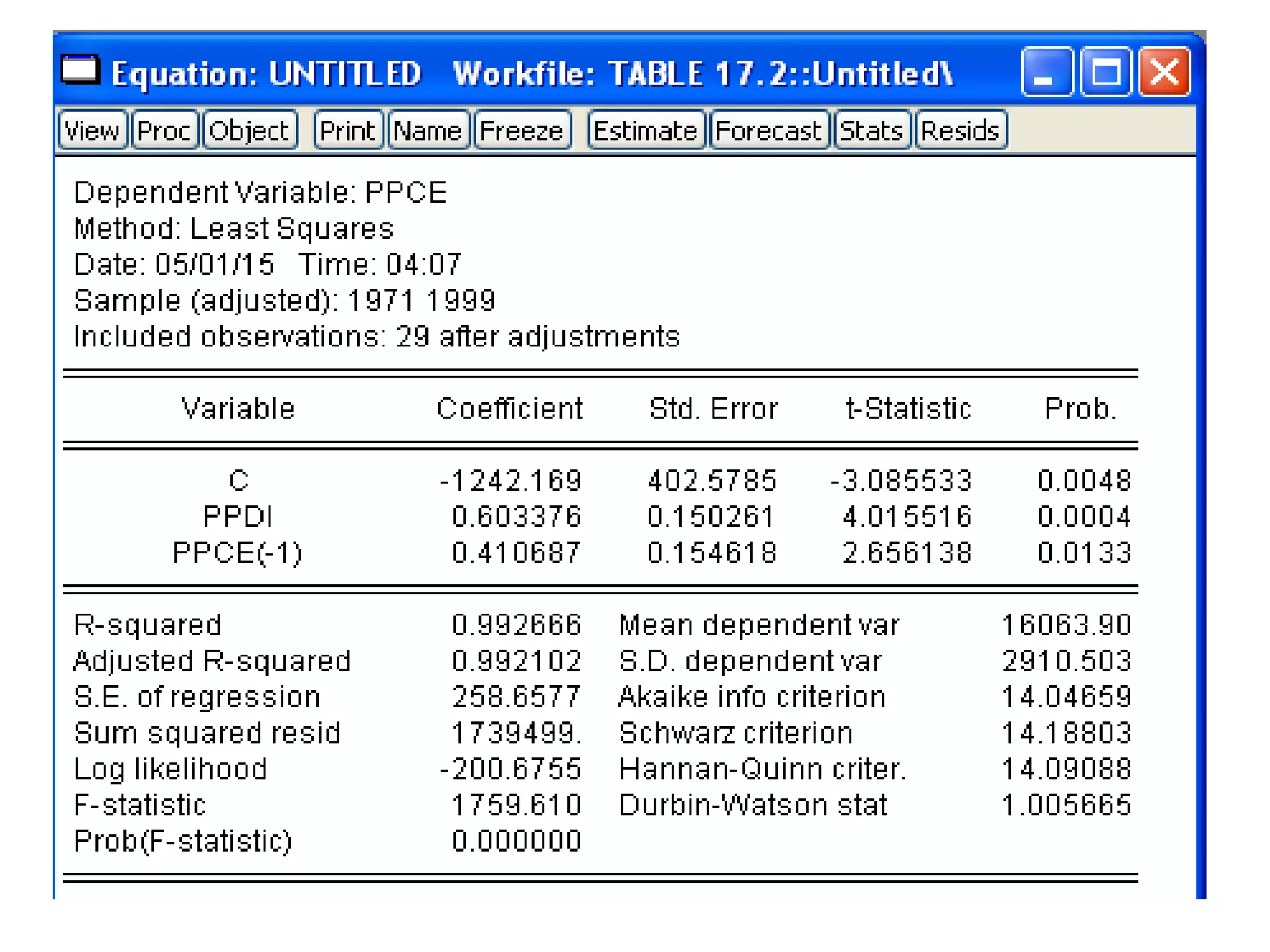
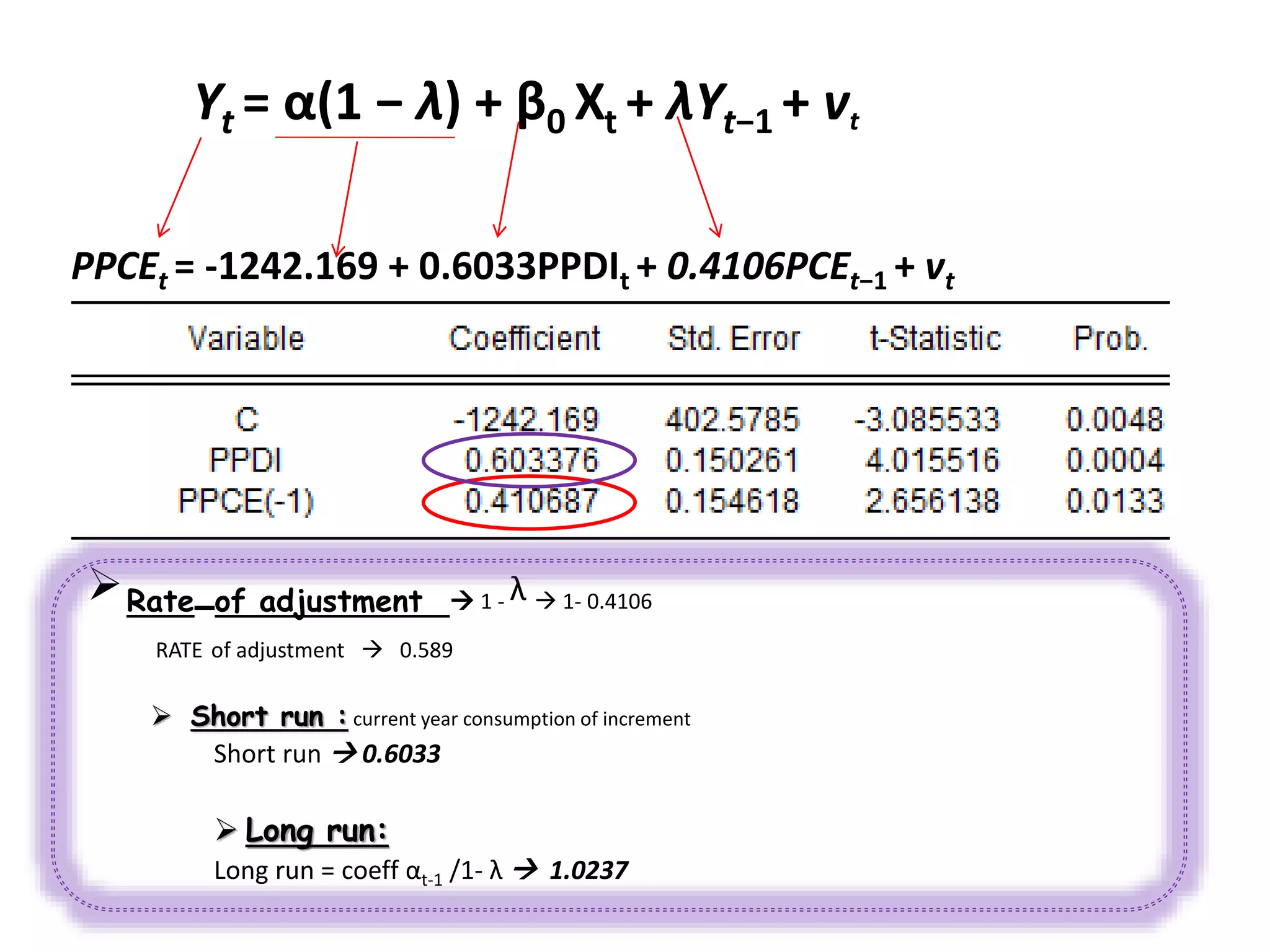
Yt = α (1 − λ) + β0 Xt + λ Yt−1 + vt
PPCEt = -1242.169 + 0.6033PPDIt + 0.4106PCEt−1 + vt