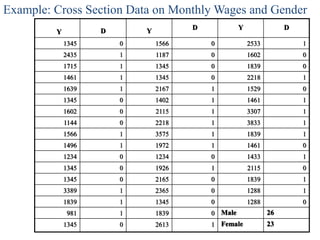
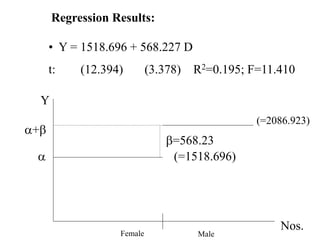
Dummy variables allow qualitative or categorical variables to be included in regression models. They take values of 0 and 1 to indicate absence or presence of a characteristic. The document discusses different types of dummy variable models including ANOVA models with all dummy explanatory variables and ANCOVA models with both dummy and quantitative variables. It provides an example of an ANOVA model to examine gender discrimination in wages. Coefficients on dummy variables represent differences in intercepts between categories. Interactive dummy variable models allow examination of effects that vary across categories of two or more qualitative variables, such as differences in wages between gender-race groups. Choice of reference categories does not change overall conclusions.

1. Dummy Variable
Regression Models

2. What is Dummy Variable?
• Variables that are essentially qualitative in
nature (or) variables that are not readily
quantifiable
• Examples: gender, marital status, race,
colour, religion, nationality, geographical
location, political/policy changes, party
affiliation

3. Other Names for Dummy Variable
Indicator variables
Binary variables
Categorical variables
Dichotomous variables
Qualitative variables

4. Why Dummy Variable Regression?
• To include qualitative variables as an
explanatory variable in the regression
model
• Example: If we want to see whether gender
discrimination has any influence on
earnings, apart from other factors

5. How to quantify qualitative aspect?
• By constructing artificial variables that take
on values of 1 or 0 (zero)
• 1 indicates presence of that attribute
• 0 indicates absence of that attribute
• Example:
(1) Gender = 1 if the respondent is female
= 0 if the respondent is male
(2) Time = 1 if war time; 0 if peacetime
• Here variables with values 1 and 0 are
called dummy variables

6. Types of Dummy Variable Models
(1) Analysis of Variance (ANOVA) Model: All
explanatory variables are dummy variables
(2) Analysis of Covariance (ANCOVA) Model:
Mix of quantitative and qualitative
explanatory variables

7. ANOVA Model
• Suppose we want to measure impact of
GENDER on wages/employee compensation
• In particular, we are interested to know
whether female employees are
discriminated against their male
counterparts
• Gender is not strictly quantifiable

8. • Hence, we describe gender using dummy
variable
D = 1 if male respondent
= 0 if female respondent [reference group]
Let the regression model as
Yi =  +  D + ui (1)
(where Y-Monthly salary)

9. • This specification helps us to see whether
gender makes difference in salary.
• Interpretation of model (1):
• Taking expectation of (1) on both sides, we get
• Mean salary of male as
E (Yi/D=1) =  + 
• Mean salary of female as
E (Yi/D=0) = 

10. • Note, mean salary of female is given by
intercept 
• Coefficient  tells by how much mean salary
of male workers differ from mean salary of
female workers (or) simply difference in
average salary between men & women -
called differential intercept coefficient
•  is attached to category which is assigned
dummy variable value of 1 (here male)

11. • Intercept () belongs to the category for
which zero dummy variable value is assigned
(here female)
• The category which is assigned zero dummy is
known as benchmark/control/reference
category
• Intercept value represents mean value of
benchmark category
• All comparisons (with ) are made in relation
to benchmark category

12. • Hypothesis testing:
• Done in the usual way
• H0 :  = 0 [No gender discrimination in salary
determination/no statistically significant
difference in salaries between males and
females]
• H1 :   0 [Gender discrimination is present in
salary determination]
• Use t – statistics
• If  is significantly different from zero, we can
accept alternate hypothesis

13. Example: Cross Section Data on Monthly Wages and Gender
Y D Y D Y D
1345 0 1566 0 2533 1
2435 1 1187 0 1602 0
1715 1 1345 0 1839 0
1461 1 1345 0 2218 1
1639 1 2167 1 1529 0
1345 0 1402 1 1461 1
1602 0 2115 1 3307 1
1144 0 2218 1 3833 1
1566 1 3575 1 1839 1
1496 1 1972 1 1461 0
1234 0 1234 0 1433 1
1345 0 1926 1 2115 0
1345 0 2165 0 1839 1
3389 1 2365 0 1288 1
1839 1 1345 0 1288 0
981 1 1839 0 Male 26
1345 0 2613 1 Female 23

14. Regression Results:
• Y = 1518.696 + 568.227 D
t: (12.394) (3.378) R2=0.195; F=11.410
Female Male
 (=1518.696)
+
=568.23
(=2086.923)
Y
Nos.

15. • Results show mean salary of female workers
is about Rs.1519
• Mean salary of male workers is increased by
Rs.568 (i.e. 1519 + 568 = 2087)
• t statistics reveal that mean salary of male is
statistically significantly higher by about
Rs.568

16. Does conclusion of model change if we
interchange dummy values?
Suppose Yi =  +  D + ui
where Y = Hourly wage
D = Gender (1= Male; 0 – Female)
Now, if we interchange dummy values as (1= Female; 0-
Male), it will not change overall conclusion of original
model (see figure)
Only change is, now “otherwise” category has become
benchmark category and all comparisons are made in
relation to this category
• Hence, choice of benchmark category () is strictly up to
the researcher

17. Extension of ANOVA Model
• Can be extended to include more than one
qualitative variable
Yi =  + 1 D1 + 2 D2 + ui
where Y = Hourly wage
D1= Marital status (1= married; 0 - otherwise)
D2= Region of residence (1= south; 0 – otherwise)
Which is the benchmark category here?
Unmarried, non-south residence

18. • Mean hourly wages of benchmark category is 
• Mean wages of those who are married is  + 1
• Mean wages of those who live in south is  + 2

20. ANCOVA Model
• Consists a mixture of qualitative and
quantitative explanatory variables
• Suppose, in our original model (1) we include
number of years of experience as an additional
variable
• Now we can raise one more question: between
2 employees with same experience, is there a
gender difference in wages?

21. • We can express regression model as
Yi = 1 + 2 D +  Xi + ui
where D is dummy; Xi is experience variable
• Now, mean salary of male is
E (Yi/D=1,X) = 1 + 2 +  Xi
• Mean salary of female is
E (Yi/D=0,X) = 1 +  Xi
• Slope is same for both categories (male &
female), only intercept differs
Slope

22. What does common slope mean?
• 2 measures average difference in salary between
male and female, given the same level of experience
• If we take a female and male with same levels of
experience, 1 + 2 represents salary of male, on
average, and 1 salary of female on average
• Note that since we controlled for experience in the
regression, the wage differential can’t be explained by
different average levels of experience between male
and female

23. • Hence, we can conclude that wage differential is
due to gender factor

24. Diagrammatic Explanation
X
Y
1 + Xi
1+2+Xi
Constant Term 1 – intercept for base group;
1 + 2 – intercept for male; and
2 measures the difference in intercept
1
2
1+2
Slope

25. Regression Estimation Results:
Y (Cap) = 1366.267 + 525.632 D +19.807 X
(8.534) (3.114) 1.456)
R2=0.48; F = 6.901
Intercept for female (base) Group 1 =1366.27. It
measures mean salary of female
Intercept for male Group, 1 + 2 = 1891.90. It
measures mean salary of male, of which 525.63 (2) is
average difference in salary between male and female
 (i.e. 19.81) – as no. of years of experience goes up
by 1 year, on average, a workers (male or female)
salary goes up by Rs.19.81

26. 2 – difference in intercept is 525.63 and is
statistically significant at 5% level.
Therefore, we can reject the null hypothesis
of no gender differential

27. Example: Several qualitative variables, with
some having more than two category:
• Example: Consumption function analysis.
• Suppose there are three qualitative factors:
gender, age of household head and education
level of head.
• Define dummy variables as:
D1 = 1 if male and =0 otherwise
D2 = 1 if age <25 and =0 otherwise
D3 = 1 if age between 25 and 50 and =0 otherwise
D4 = 1 if high school education and =0 otherwise
D5= 1 if H.sc., degree and above and =0 otherwise

28. Base or Reference Groups:
Regression Model:
Ct =  +  Yt + 1D1+ 2D2 + 3D3 + 4D4 + 5D5 + ut
- intercept for female head of household
- intercept term if age of head is above 50 years
- intercept term if head’s education is below high school
In short  represents female head of household aged above
50 years and with below high school education

29. Differential intercepts or mean
compensation for other groups:
 + 1- for male household head
 + 2 – for age is less than 25 years
 + 3 - for age between 25 and 50 years
 + 4 – for high school education
 + 5 –for above high school education
If the household head is male with age 40 years and
high school education, what is the intercept?
 + 1+ 3+ 4

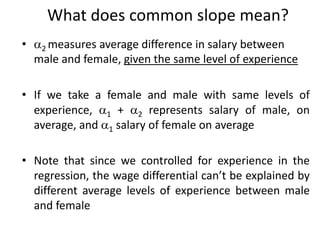
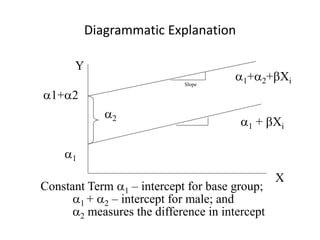
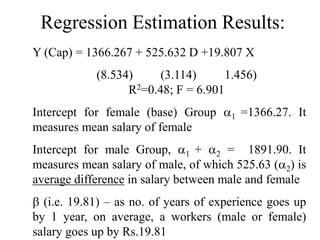
30. Interactions Involving Dummy Variables
• Consider the following model:
Yi = 1 + 2 D2i + 3 D3i +  Xi + ui ----- (1)
Yi = Hourly wage
Xi = Education (years of schooling)
D2 = 1 if female, 0 if male [GENDER]
D3 = 1 if black, 0 if white [RACE]
Note that in this model dummy variables are
interactive in nature. How?

31. • Here, if mean salary is higher for female than for
male, this is so whether they (female) are black or
white
• Similarly, if mean salary is lower for black, this is so
whether they (black) are male or female
• Implication: Effect of D2 and D3 on Y may not be
simply additive as in (1) but multiplicative as below
Male Female Black White
Black White Black White Male Female Male Female
Gender Race

32. Yi = 1 + 2 D2i + 3 D3i + 4 (D2iD3i) +  Xi + ui -- (2)
Eq (2) includes explicitly interaction between GENDER &
RACE, i.e. D2iD3i
2 – differential effect of being a female (gender alone)
3 – differential effect of being a black (race alone)
4 – differential effect of being a black female (g & r)
1 – Male white (base category)
Note: While running (2), simply multiply D2iD3i values
Eq (2) is a different way of finding wage differentials
across all gender-race combinations

33. In other words interactive model (eq.2) allows us
to obtain estimated wage differential among all 4
groups (male, female, black & white). How?
(i) Black Female (Yi/D2i=1, D3i=1, Xi)
1 + 2 + 3 + 4
(ii) Black Male (Yi/D2i=0, D3i=1, Xi)
1 + 3
(iii) White Male (Yi/D2i=0, D3i=0, Xi)
1
(iv) White Female (Yi/D2i= 1, D3i=0, Xi)
1 + 2

34. Male Female Married (M) Unmarried (UM)
M UM M UM Male Female Male Female
Gender Marital status