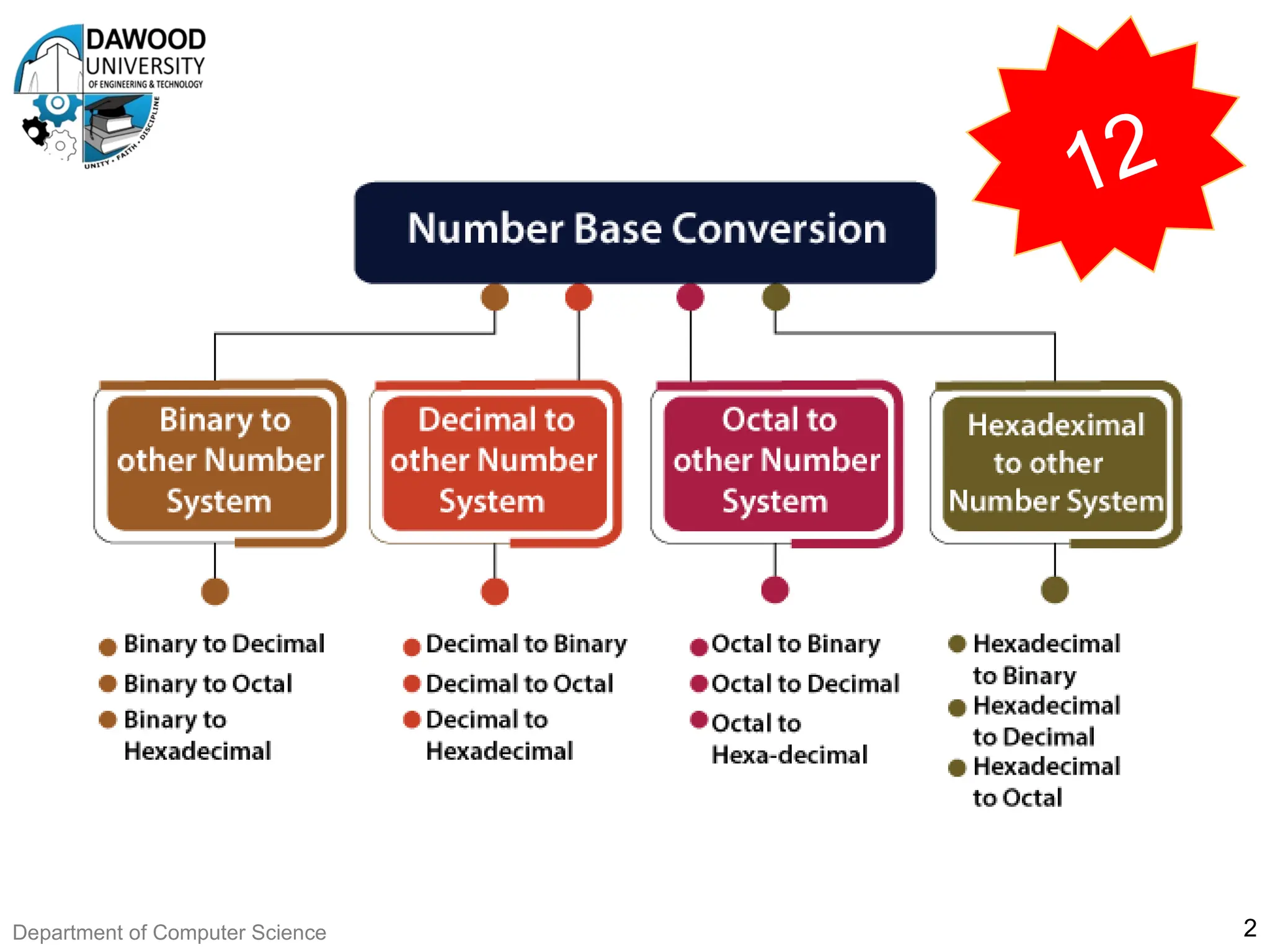
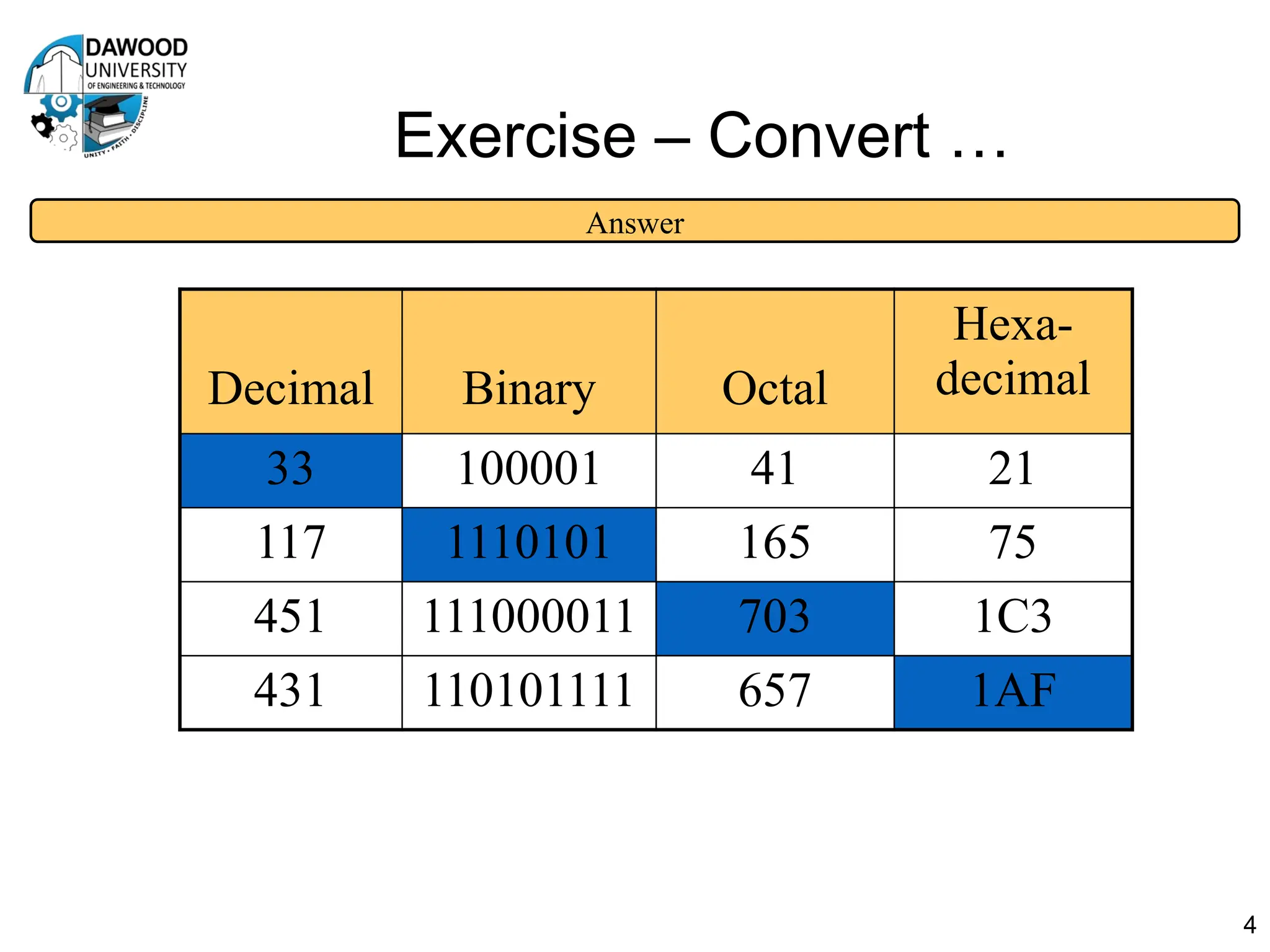
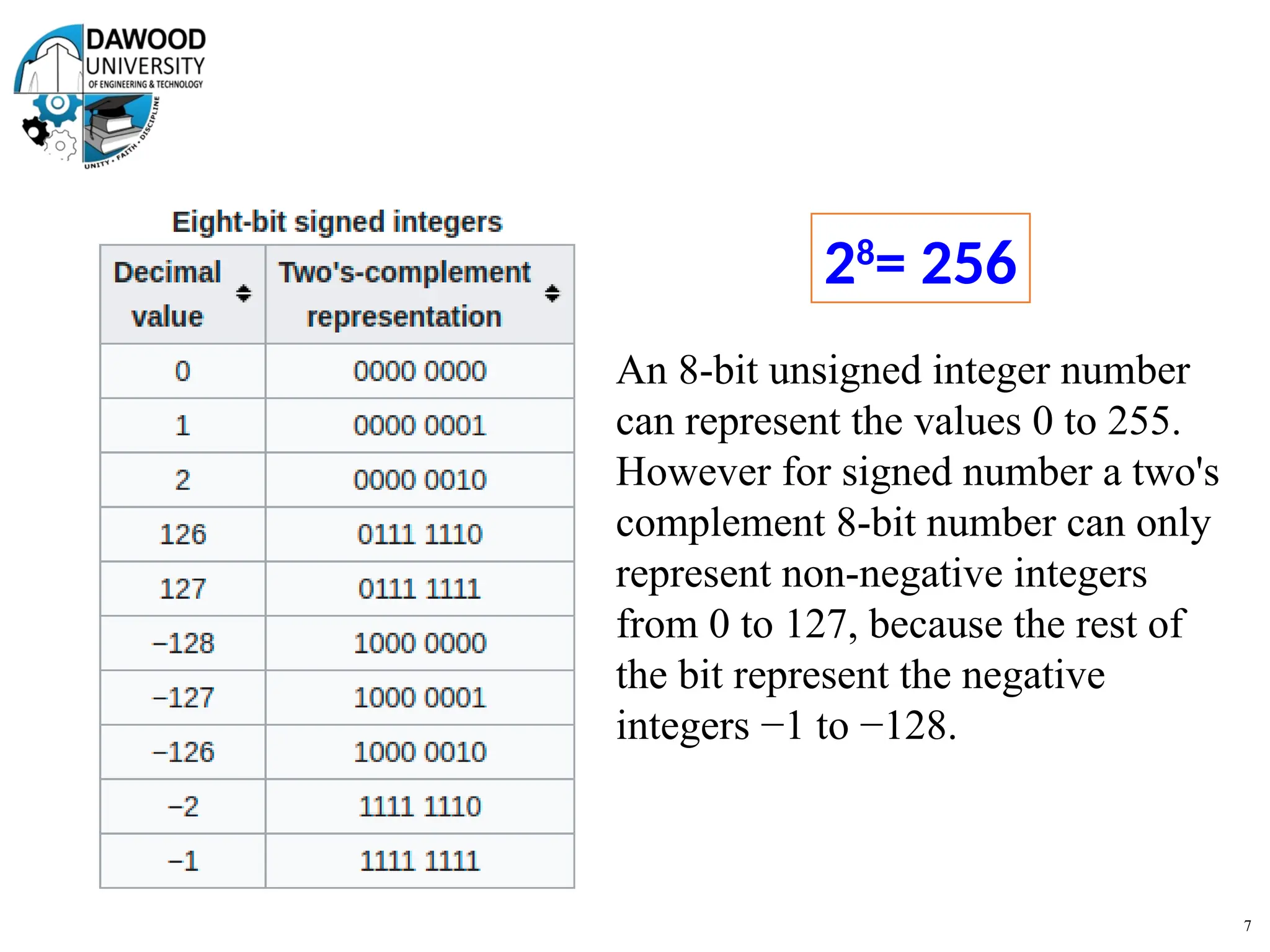
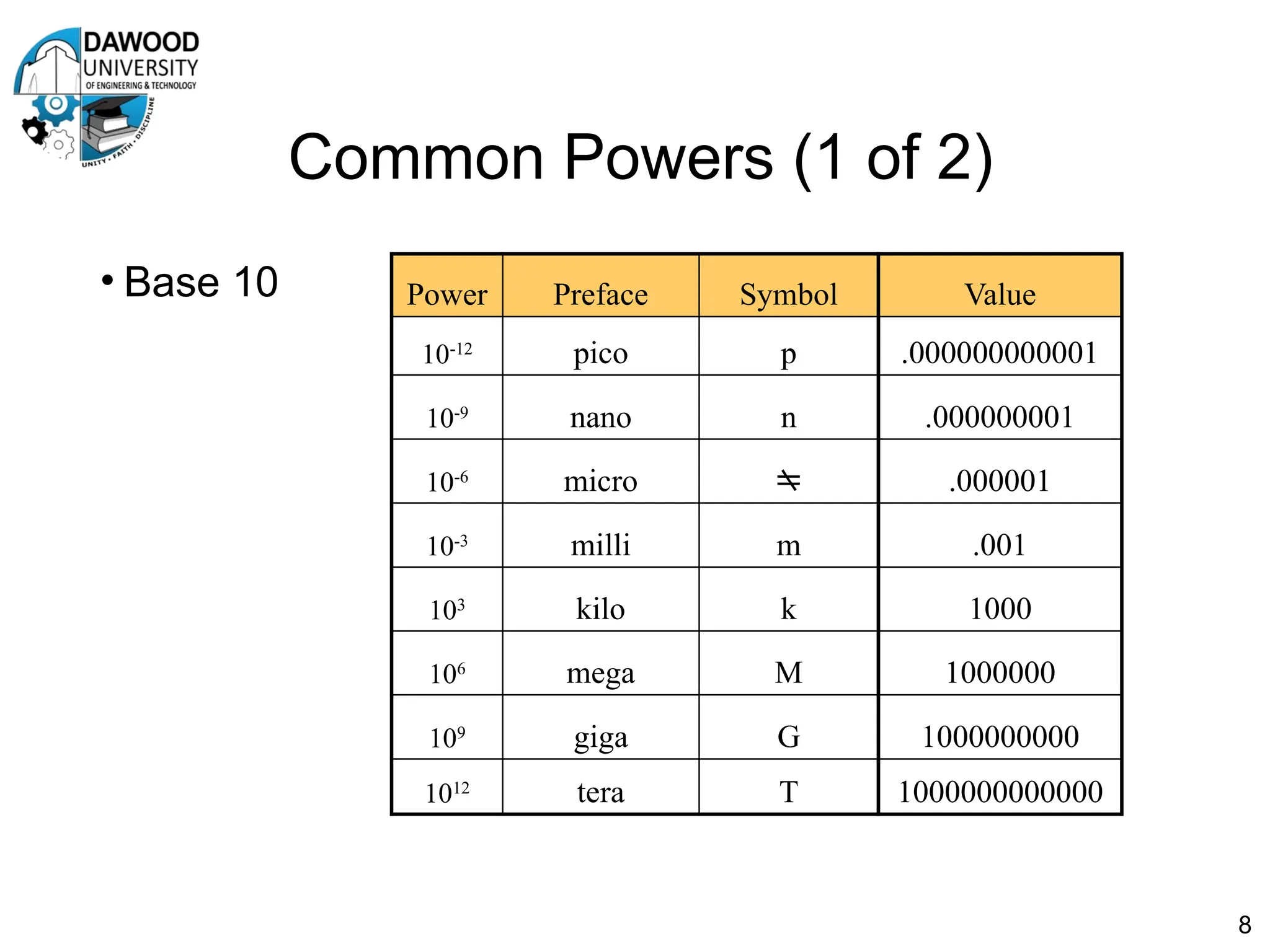
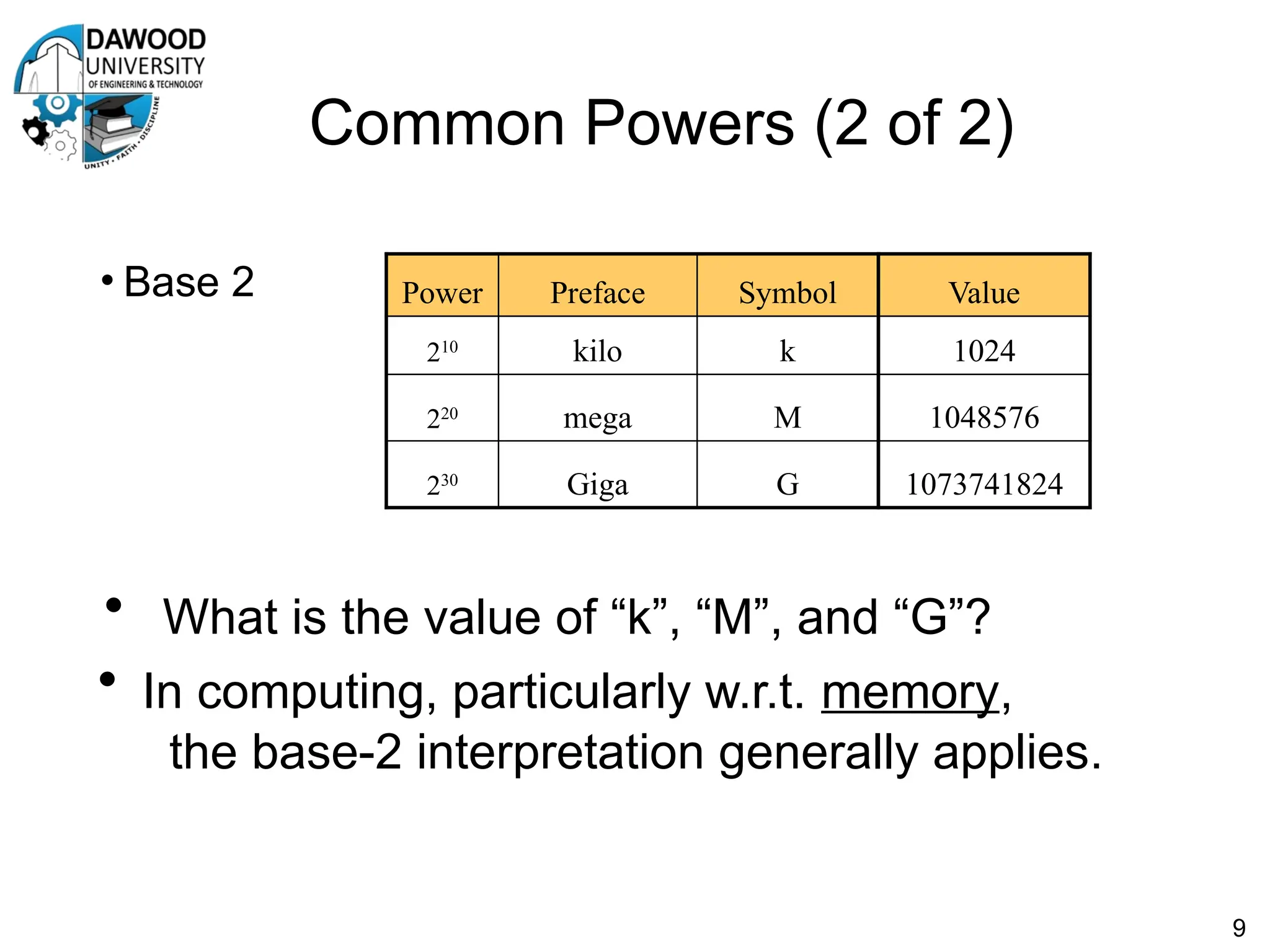
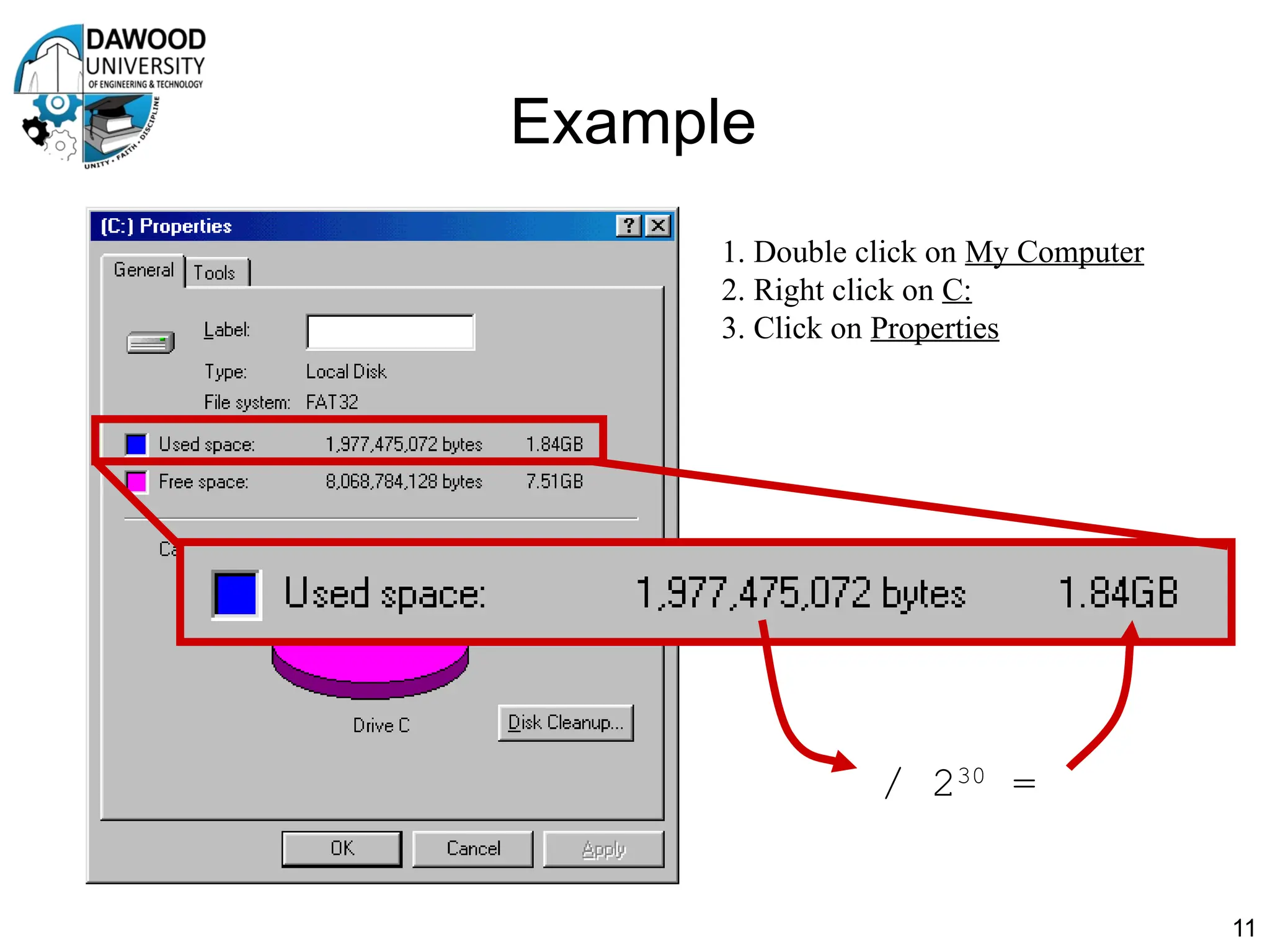
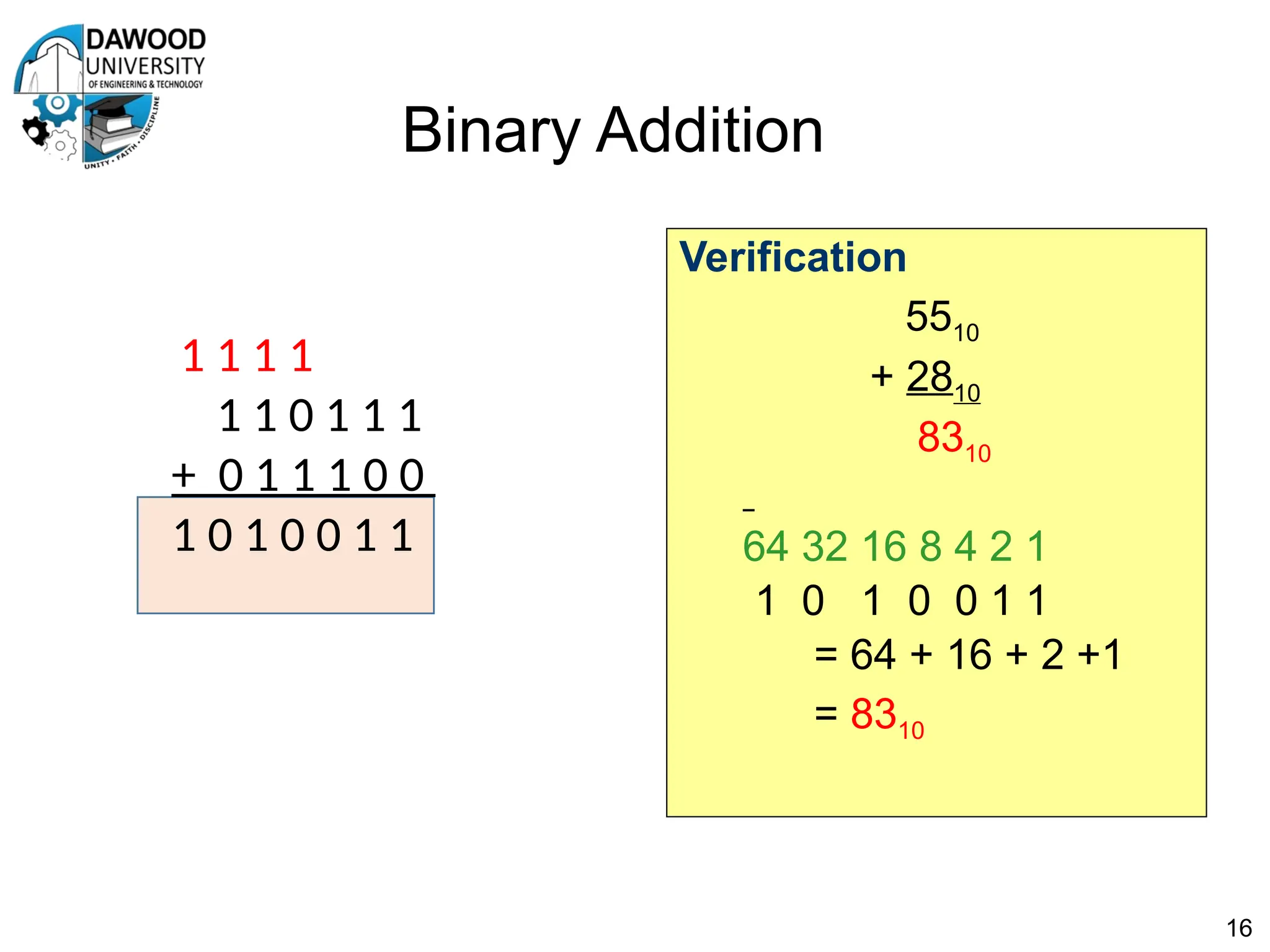
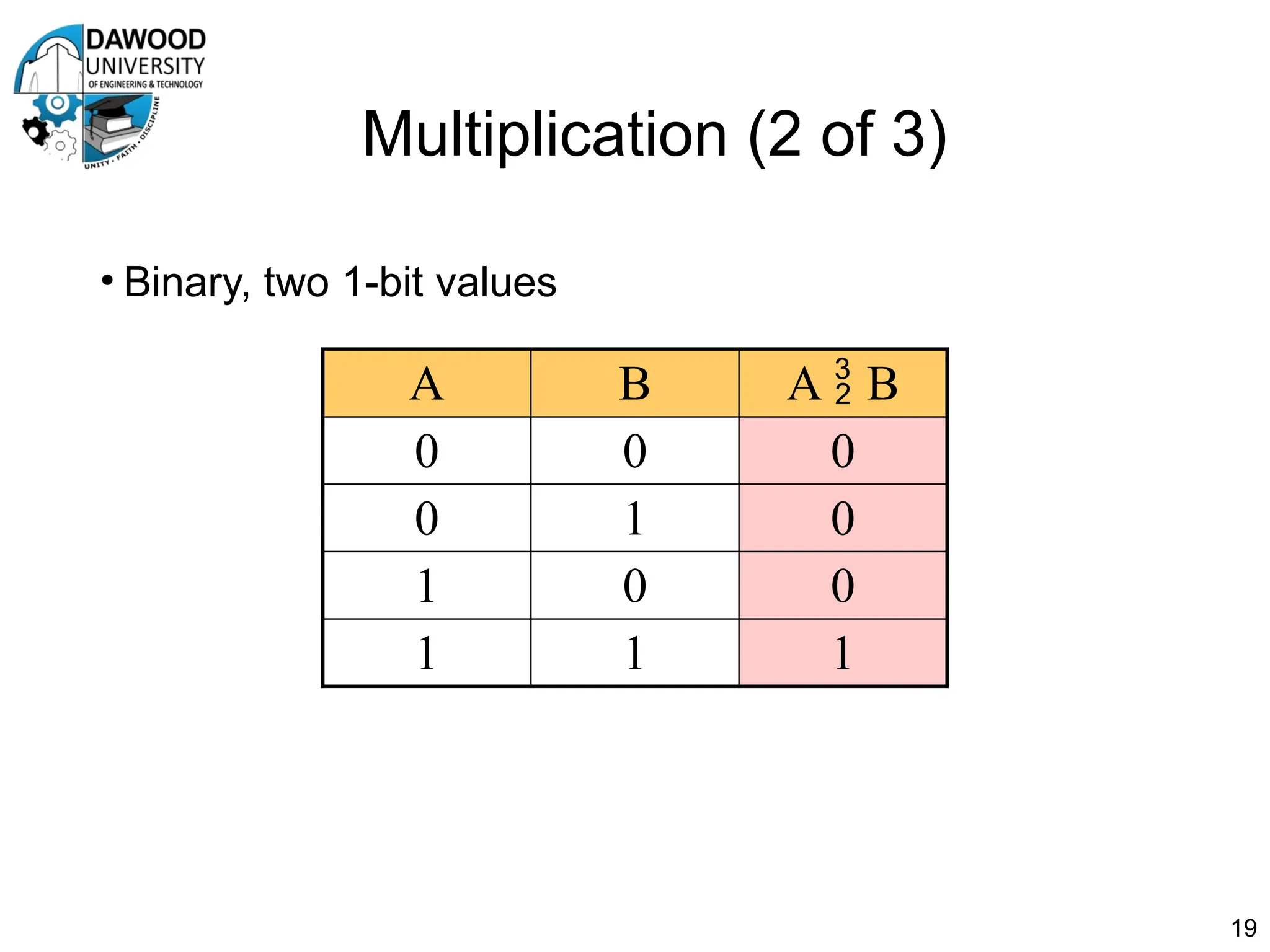
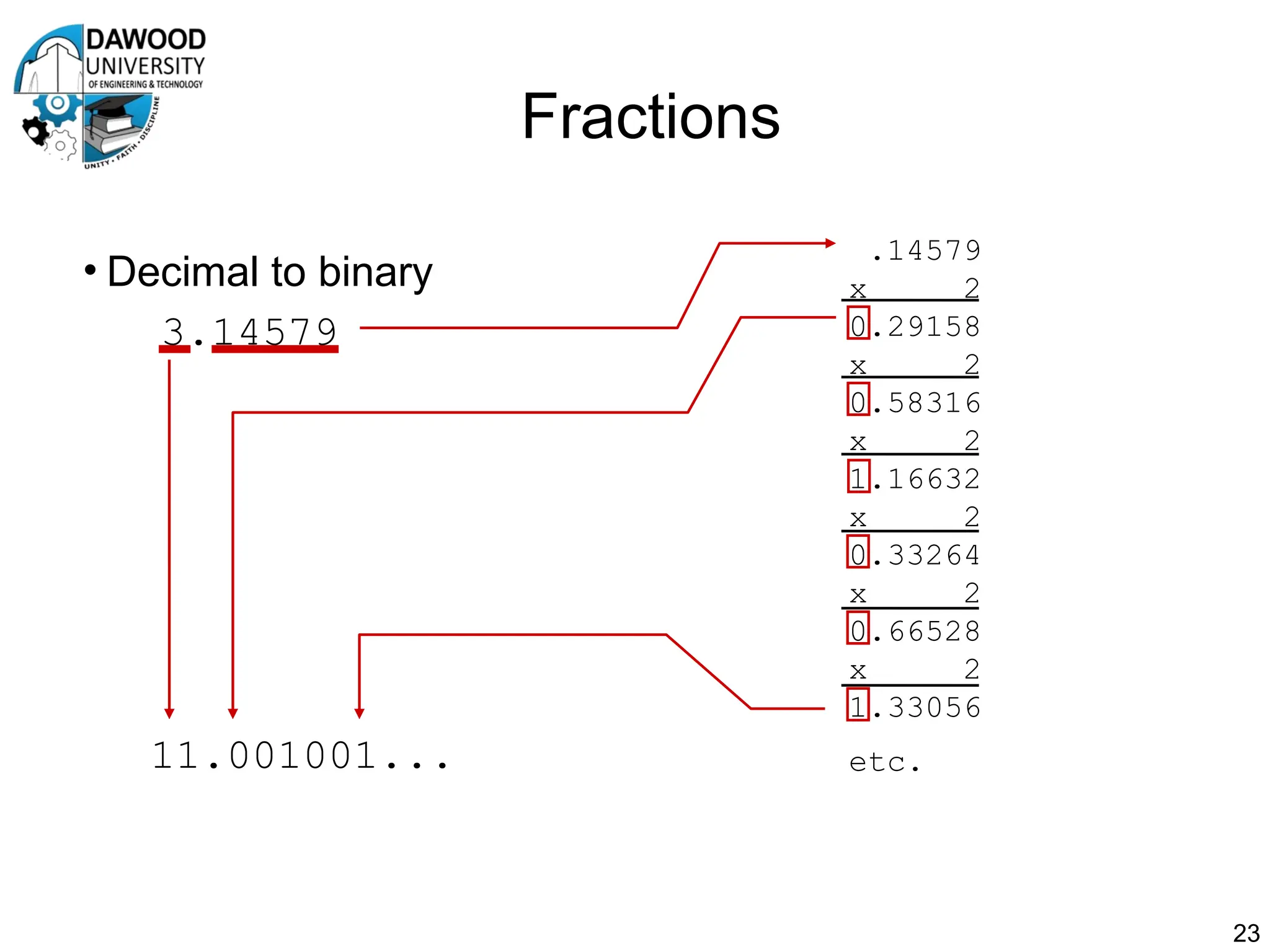
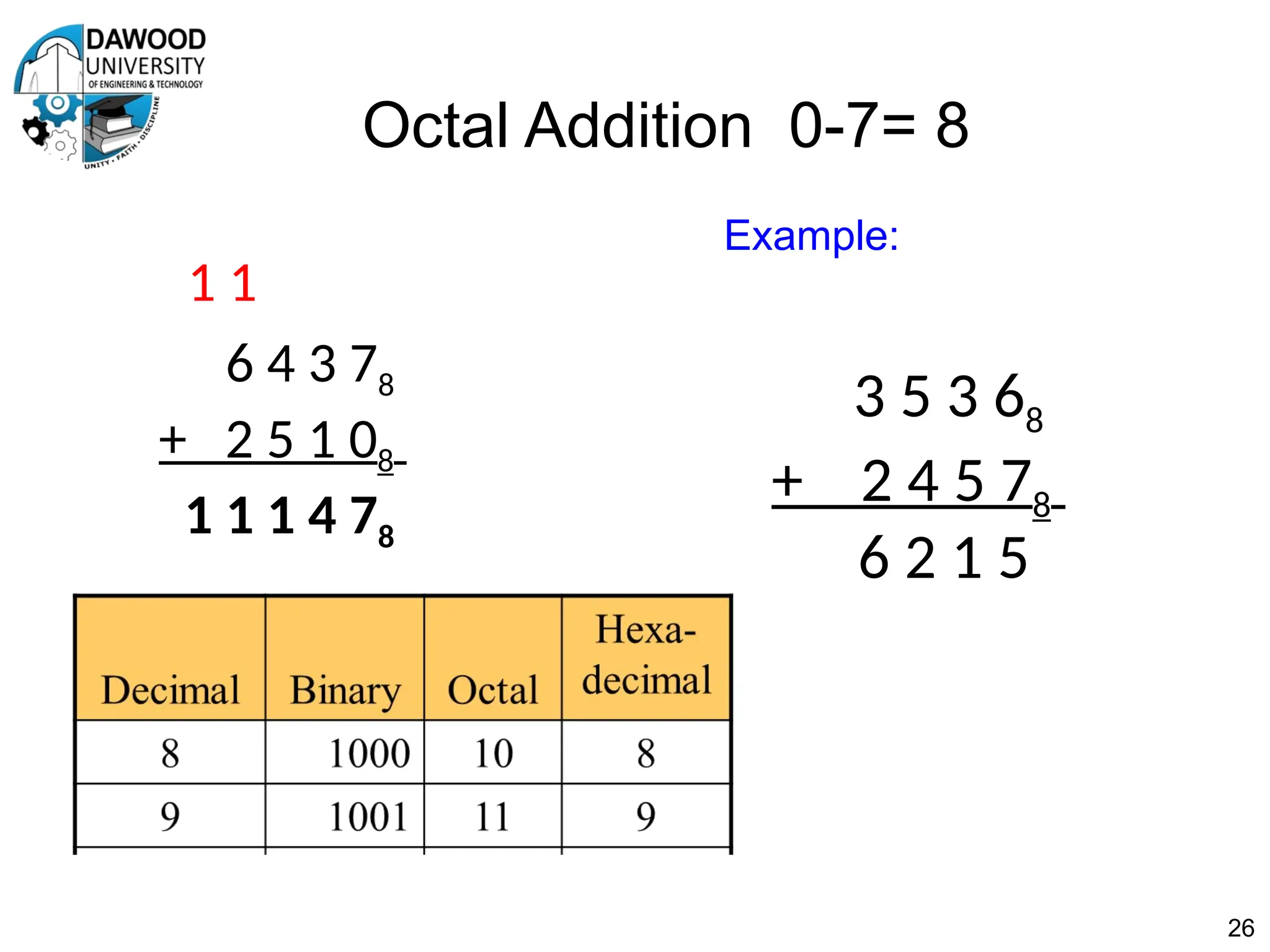
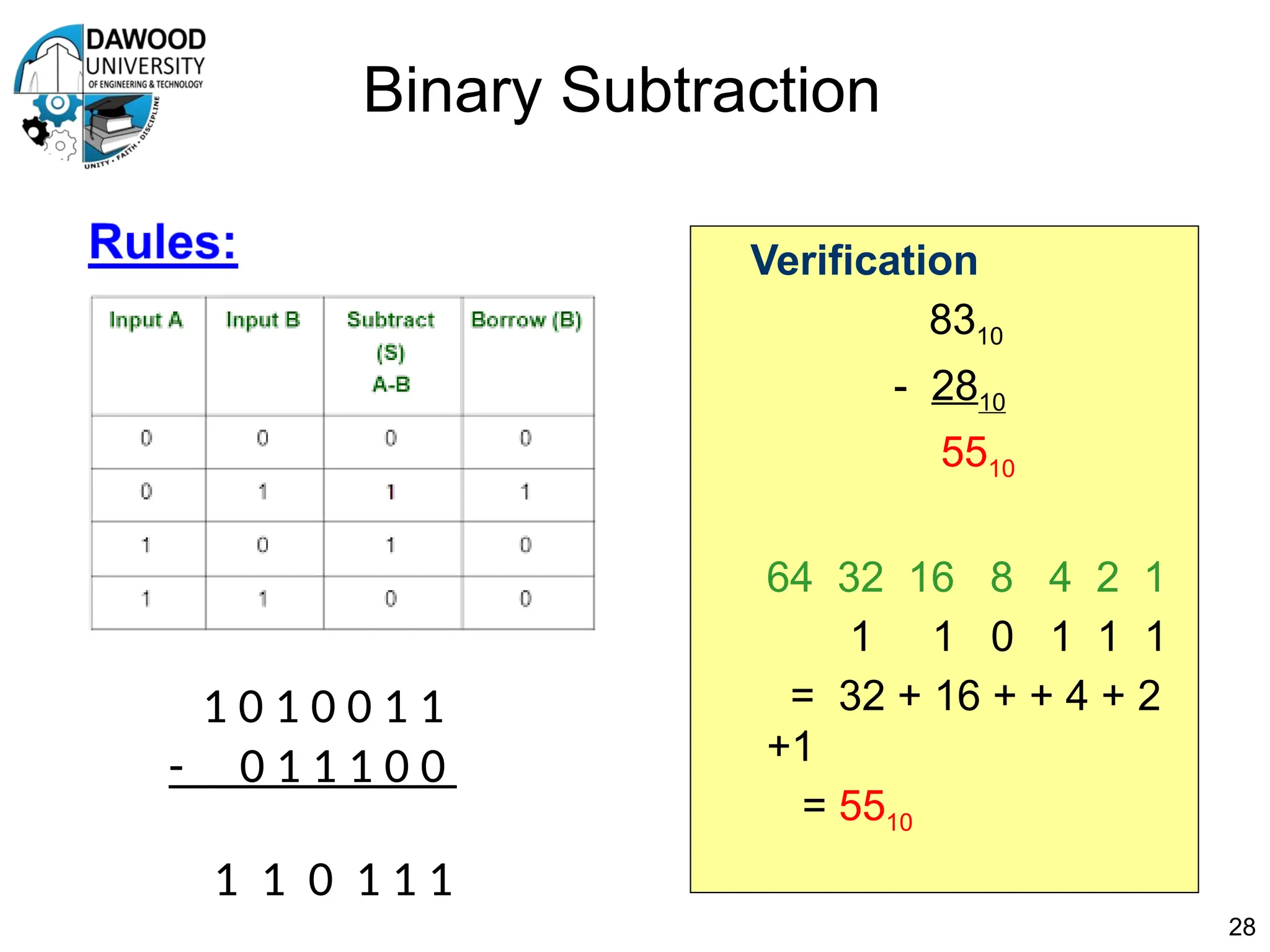
The document is a lecture notes outline focused on numbering systems (binary, octal, hexadecimal) and arithmetic operations, including conversion exercises and examples for binary addition, subtraction, and multiplication. It introduces key concepts such as two's complement representation and the different ranges of signed and unsigned numbers. Various arithmetic operations, including addition and multiplication in different numeral systems, are covered with quizzes and exercises for practice.

1. Easy Approach:
Numbering Systems
And Arithmetic Operations On Hex,
Binary, And Octal
Lecture-03
Teacher: Dr. Syed Ali Asgher
Email: alisyed5@duet.edu.pk

2. 2
12
Department of Computer Science

3. Exercise – Convert ...
3
Don’t use a calculator!
Decimal Binary Octal
Hexa-
decimal
33
1110101
703
1AF
Skip answer Answer
Department of Computer Science

4. Exercise – Convert …
4
Decimal Binary Octal
Hexa-
decimal
33 100001 41 21
117 1110101 165 75
451 111000011 703 1C3
431 110101111 657 1AF
Answer

5. What is the two’s complement?
A two's-complement system is a system in which
negative numbers are represented by the two's
complement of the absolute value.
5

6. Example
Suppose we're working with 8 bit and suppose we want to find how -28 would
be expressed in two's complement notation. First we write out 28 in binary
form.
0 0 0 1 1 1 0 0
1 1 1 0 0 1 0 0
1 1 1 0 0 0 1 1
Then we invert the digits. 0 becomes 1, 1 becomes
0.
Then we add 1.
That is how one would write -28 in 8 bit binary.
6

7. 7
An 8-bit unsigned integer number
can represent the values 0 to 255.
However for signed number a two's
complement 8-bit number can only
represent non-negative integers
from 0 to 127, because the rest of
the bit represent the negative
integers −1 to −128.
28
= 256

8. Common Powers (1 of 2)
• Base 10
8
Power Preface Symbol
10-12 pico p
10-9
nano n
10-6 micro 
10-3
milli m
103 kilo k
106 mega M
109 giga G
1012 tera T
Value
.000000000001
.000000001
.000001
.001
1000
1000000
1000000000
1000000000000

9. Common Powers (2 of 2)
• Base 2
9
Power Preface Symbol
210
kilo k
220 mega M
230
Giga G
Value
1024
1048576
1073741824
• What is the value of “k”, “M”, and “G”?
• In computing, particularly w.r.t. memory,
the base-2 interpretation generally applies.

10. 10

11. Example
11
/ 230
=
1. Double click on My Computer
2. Right click on C:
3. Click on Properties

12. Review – multiplying powers
• For common bases, add powers
12
26
 210
= 216
= 65,536
or…
26
 210
= 64  210
= 64k
ab
 ac
= ab+c

13. Arithmetic Operations on Hex,
Binary, Octal
13

14. Binary Addition
Rules:
• 0 + 0 = 0
• 0 + 1 = 1
• 1 + 0 = 1
• 1 + 1 = 2 = 102 = 0 with 1 to carry
• 1 + 1 + 1 = 3 = 112 = 1 with 1 to carry
14

15. Binary Addition
• Two n-bit values
• Add individual bits
• Propagate carries
• E.g.,
15
10101 21
+ 11001 + 25
101110 46
1
1

16. Binary Addition
1 1 1 1
1 1 0 1 1 1
+ 0 1 1 1 0 0
1 0 1 0 0 1 1
16
Verification
5510
+ 2810
8310
64 32 16 8 4 2 1
1 0 1 0 0 1 1
= 64 + 16 + 2 +1
= 8310

17. Binary Addition
Example Verification
1 0 0 1 1 1
+ 0 1 0 1 1 0 + ___
1 1 1 1 0 1
128 64 32 16 8
4 2 1
=
=
17

18. Multiplication (1 of 3)
• Decimal (just for fun)
18
35
x 105
175
000
35
3675

19. Multiplication (2 of 3)
• Binary, two 1-bit values
19
A B A  B
0 0 0
0 1 0
1 0 0
1 1 1

20. Multiplication (3 of 3)
• Binary, two n-bit values
• As with decimal values
• E.g.,
20
1110
x 1011
1110
1110
0000
1110
10011010

21. Fractions
• Decimal to decimal (just for fun)
21
3.14 => 4 x 10-2
= 0.04
1 x 10-1
= 0.1
3 x 100
= 3
3.14

22. Fractions
• Binary to decimal
22
10.1011 => 1 x 2-4
= 0.0625
1 x 2-3
= 0.125
0 x 2-2
= 0.0
1 x 2-1
= 0.5
0 x 20
= 0.0
1 x 21
= 2.0
2.6875

23. Fractions
• Decimal to binary
23
3.14579
.14579
x 2
0.29158
x 2
0.58316
x 2
1.16632
x 2
0.33264
x 2
0.66528
x 2
1.33056
etc.
11.001001...

24. Exercise – Convert ...
24
Don’t use a calculator!
Decimal Binary Octal
Hexa-
decimal
29.8
101.1101
3.07
C.82
Skip answer Answer

25. Decimal Addition
111
3758
+ 4657
8 4 1 5
25
What is going on?
1 1 1 (carry)
3 7 5 8
+ 4 6 5 7
14 11 15
- 10 10 10 (subtract the base)
8 4 1 5

26. Octal Addition 0-7= 8
1 1
6 4 3 78
+ 2 5 1 08
1 1 1 4 78
26
Example:
3 5 3 68
+ 2 4 5 78
6 2 1 5

27. Hexadecimal Addition
1 1 Example:
7 C 3 916
+ 3 7 F 216
B 4 2 B16
27
8 A D 416
+ 5 D 616
9 0 A A

28. Binary Subtraction
1 0 1 0 0 1 1
- 0 1 1 1 0 0
1 1 0 1 1 1
28
Verification
8310
- 2810
5510
64 32 16 8 4 2 1
1 1 0 1 1 1
= 32 + 16 + + 4 + 2
+1
= 5510

29. Exercise
Hexadecimal:
650E + 08C1 =
4A6 + 1B3 =
4A6 – 1B3 =
Octal:
162 + 537 =
29
Website: https://madformath.com/calculators/digital-systems/

30. Solutions
HD
650E + 08C1 = 6DCF
4A6 + 1B3 = 659
4A6 – 1B3 = 2F3
OCTAL
162 + 537 = 721
30