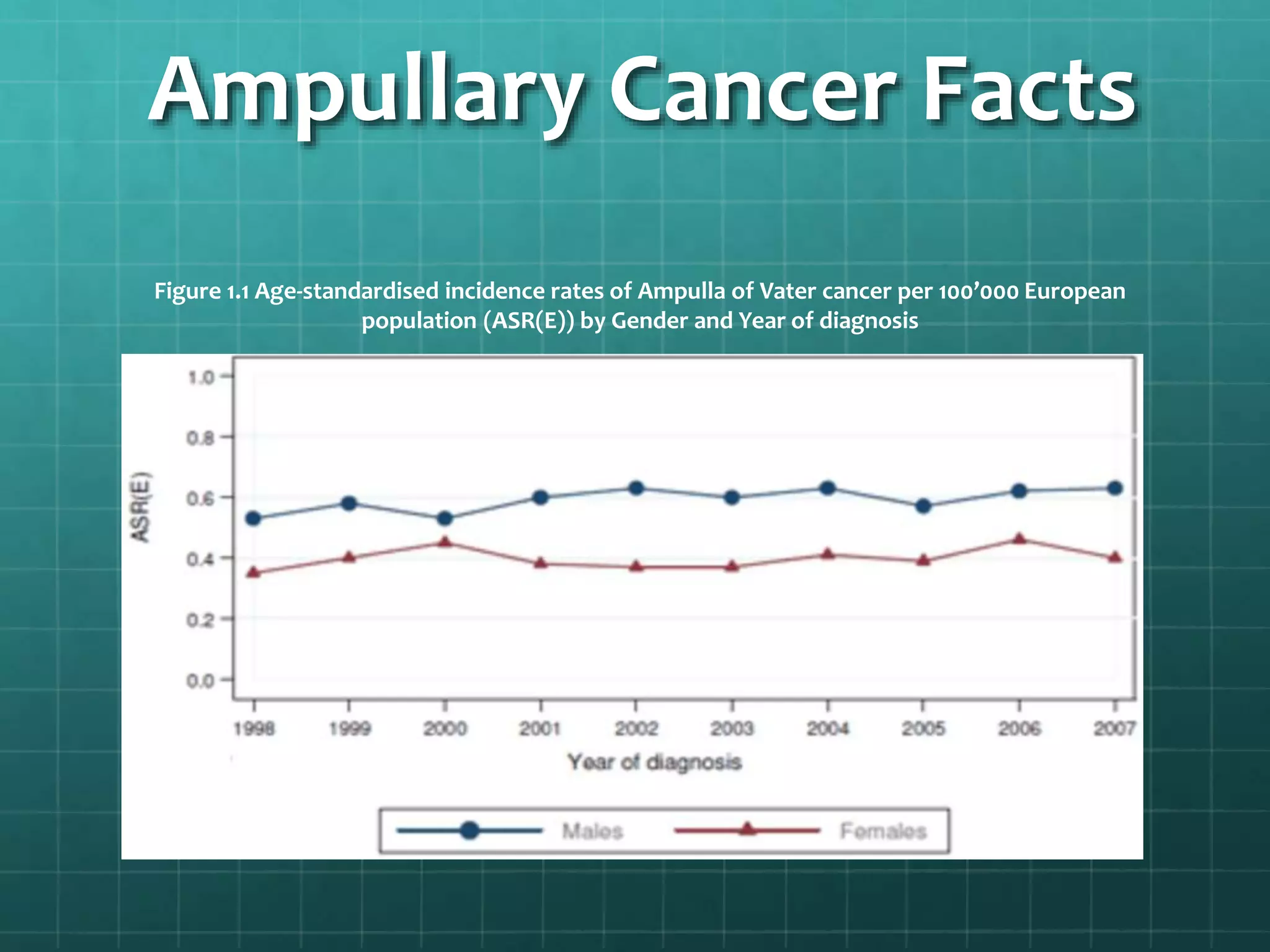
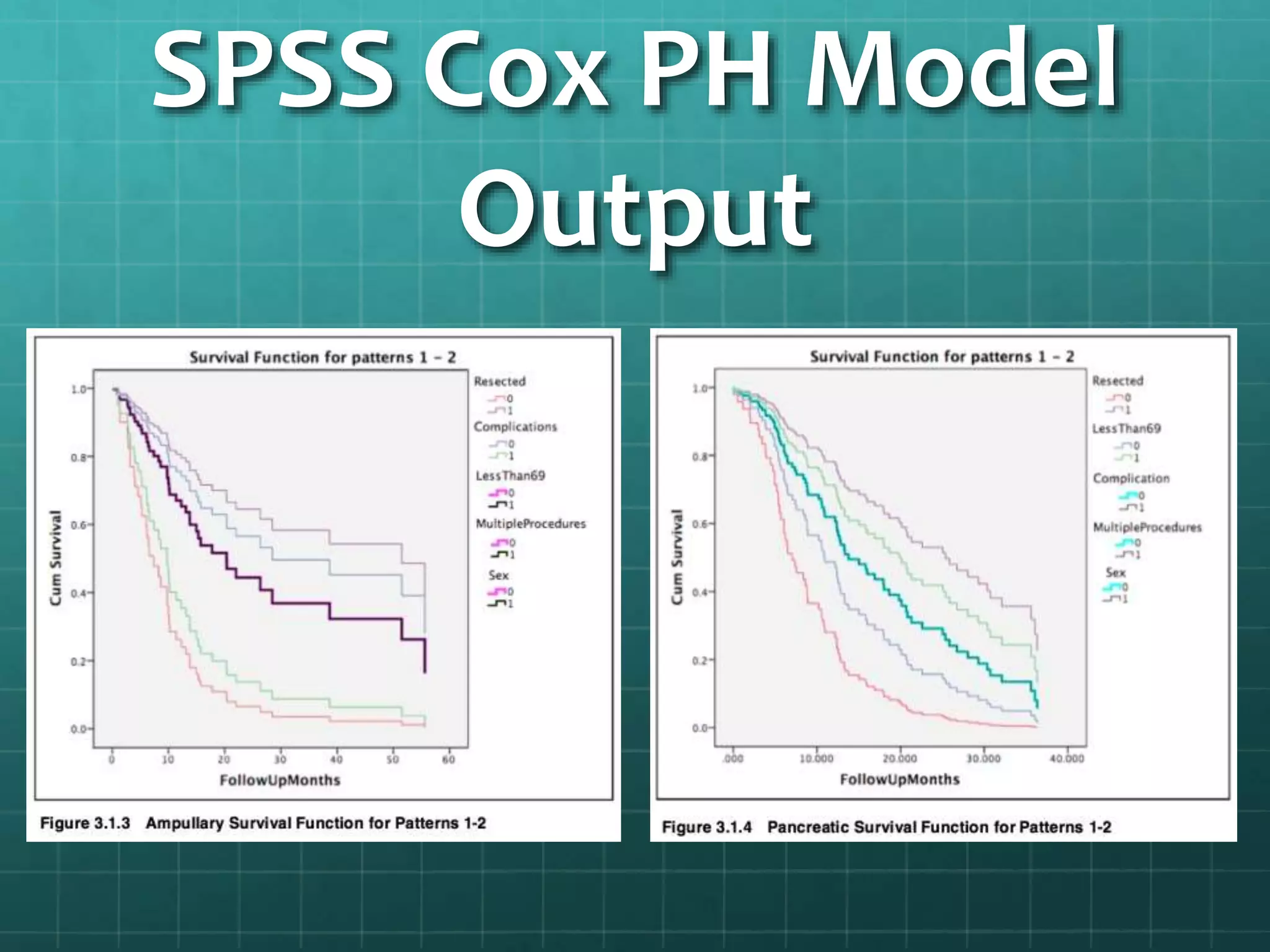
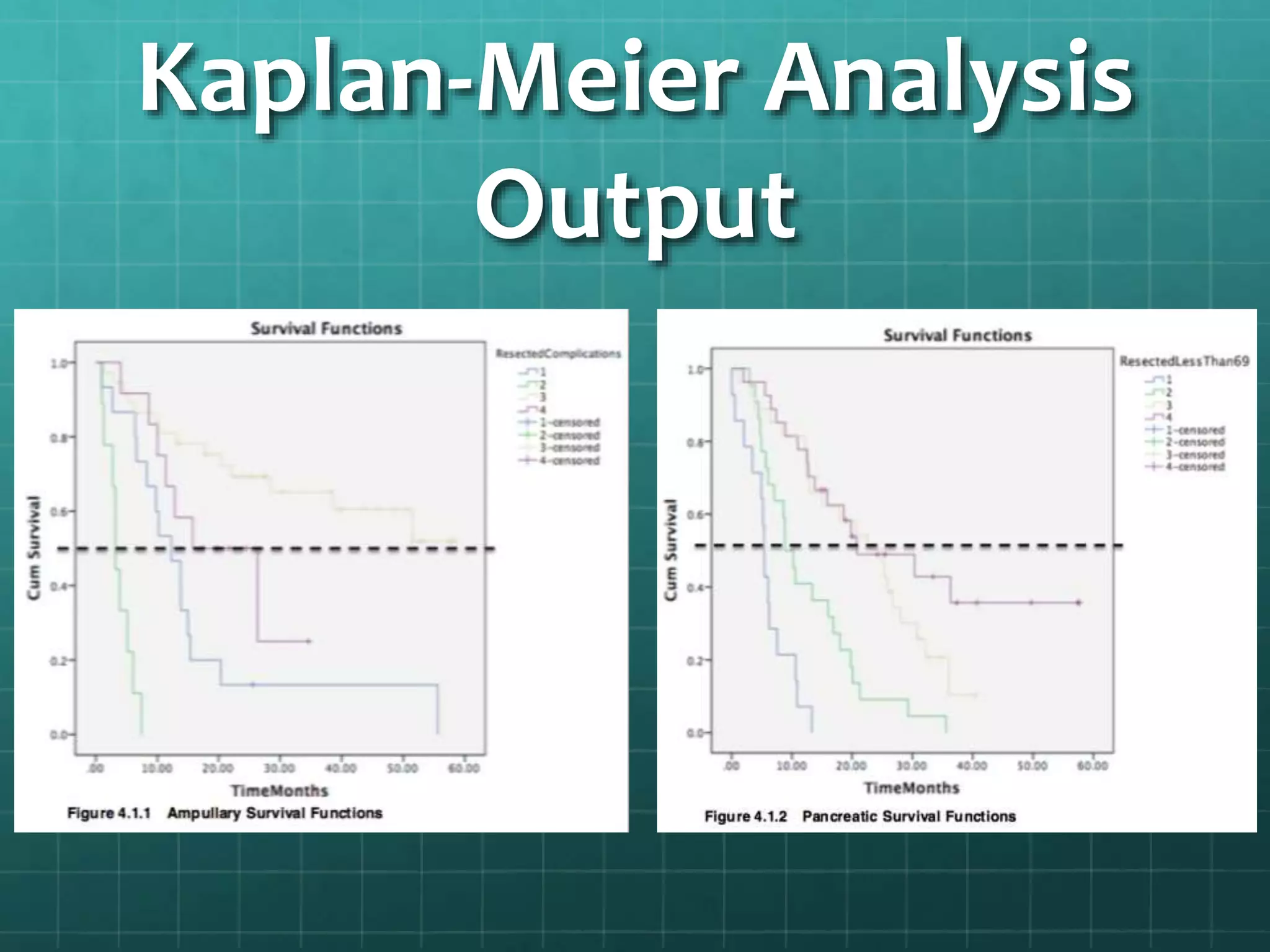
This document summarizes a study analyzing mortality rates of cancer patients. It used SPSS software and the Cox Proportional Hazard Model to analyze how variables like being "resected" and being "less than 69" affected mortality rates for ampullary and pancreatic cancer patients. The results found "resected" and "less than 69" significantly impacted survival rates. Kaplan-Meier analysis confirmed these findings and showed a 20.053% difference in survival rates between groups. The conclusion was that the null hypothesis that no variables impact mortality rates was rejected.