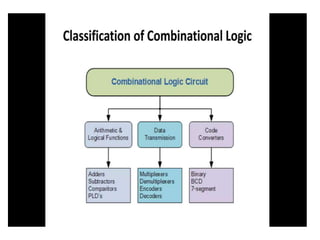
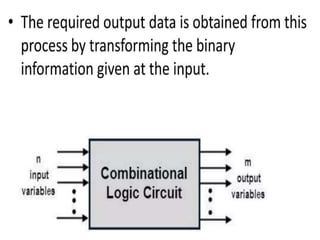
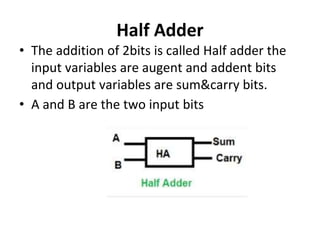
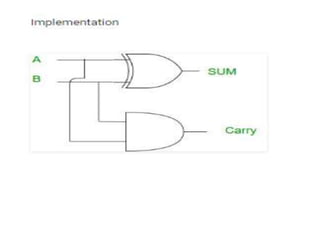
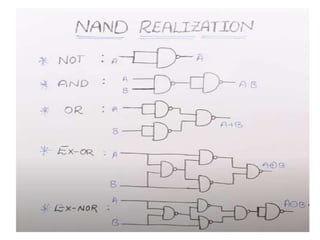
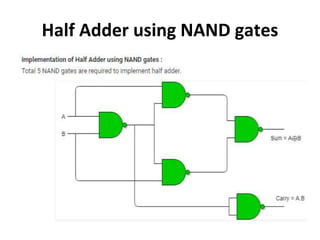
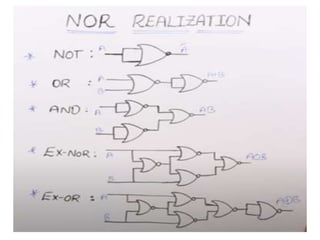
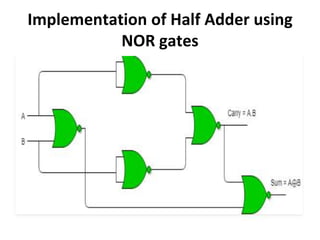
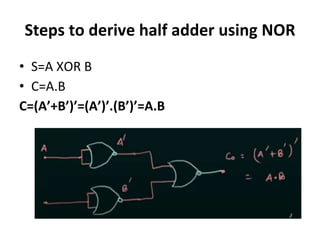
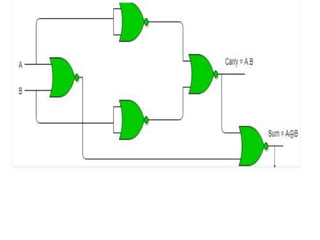
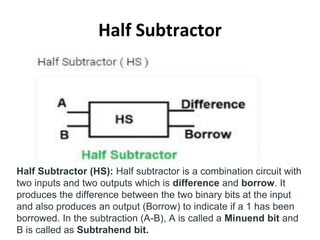
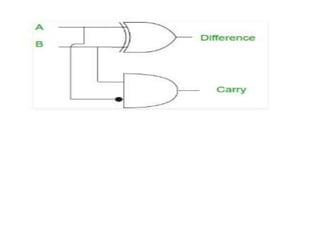
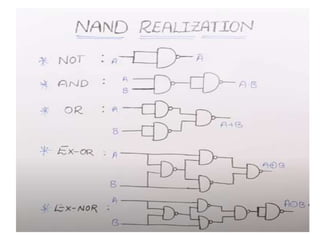
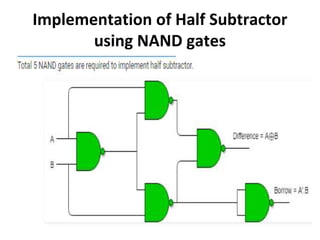
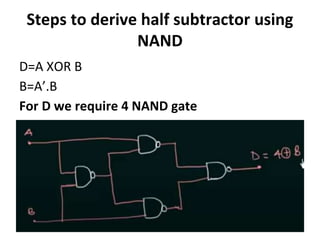
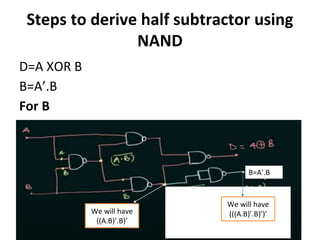
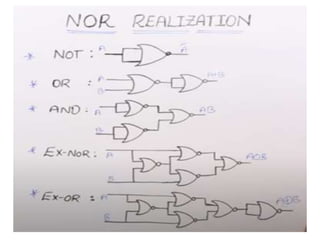
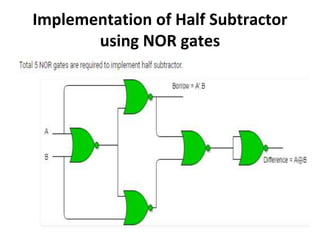
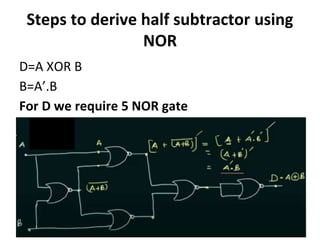
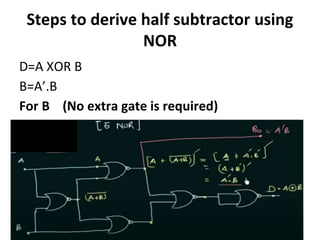
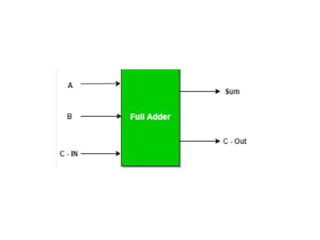
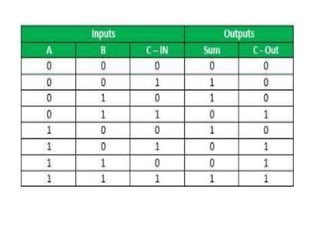
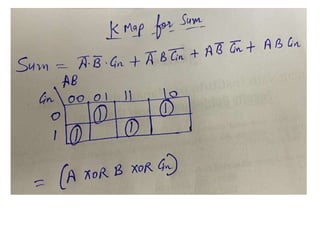
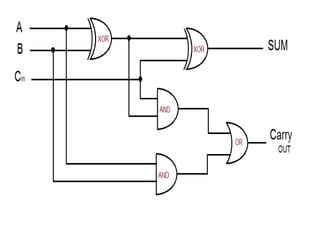
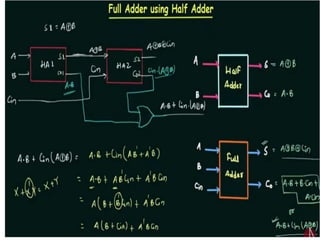
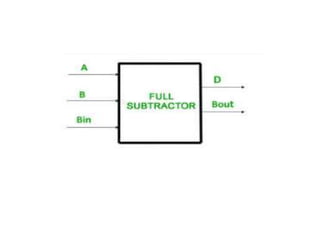
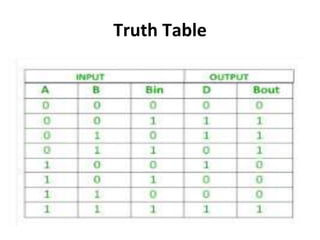
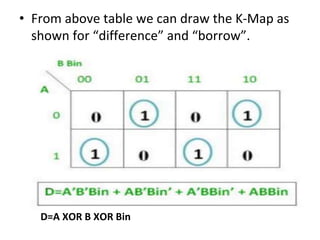
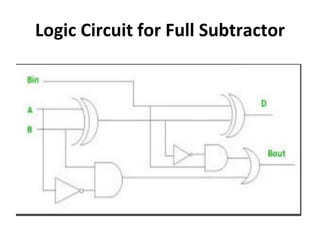
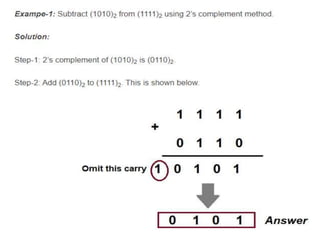
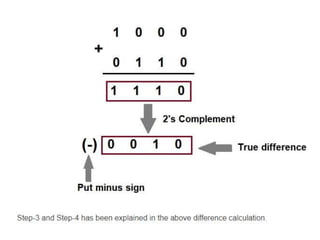
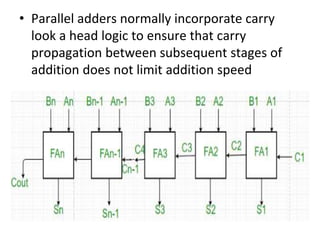
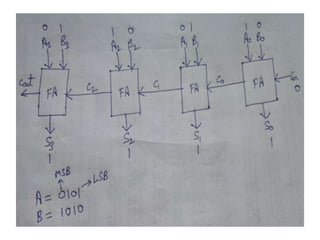
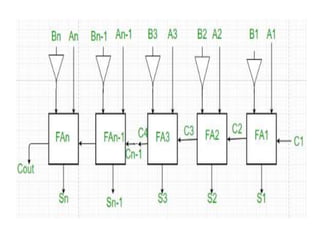
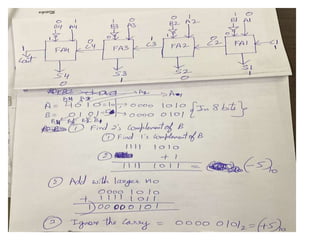
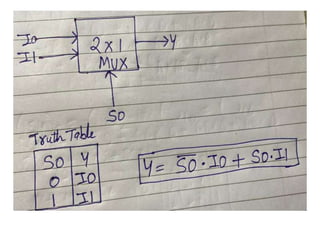
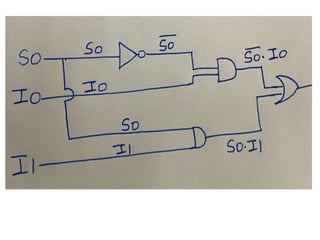
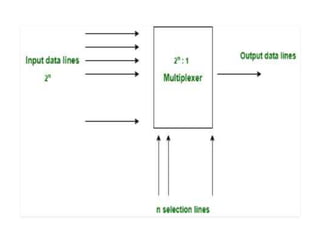
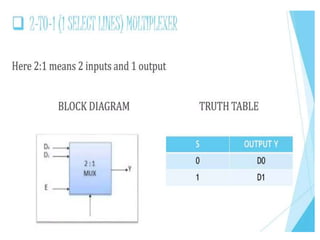
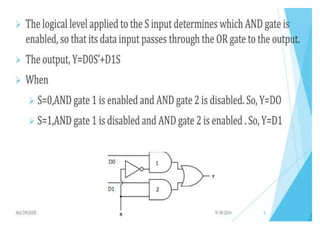
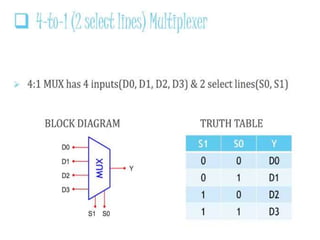
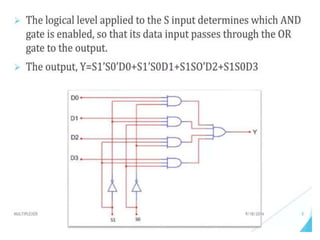
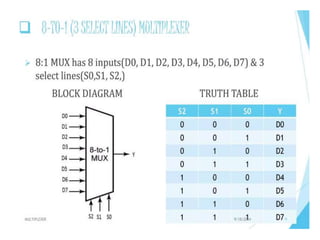
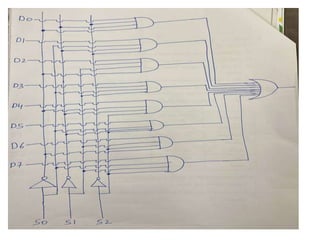
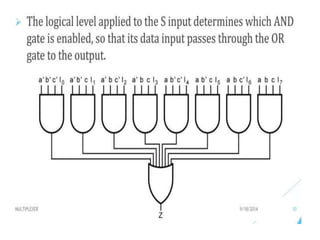
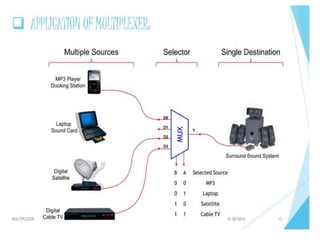
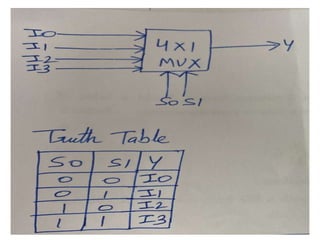
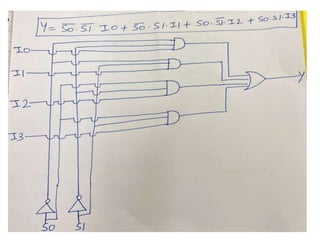
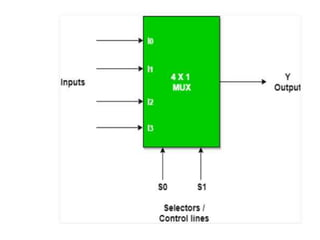
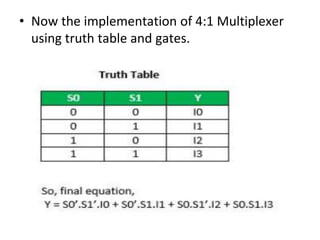
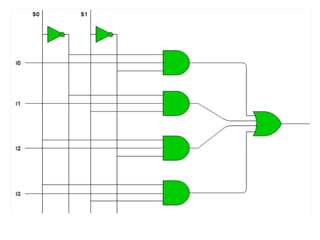
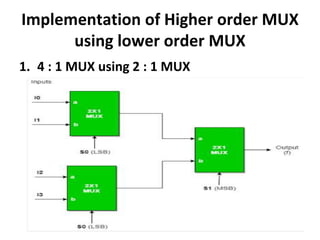
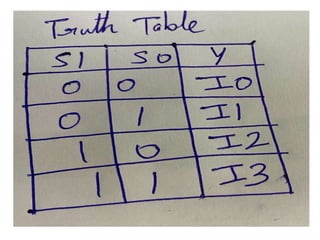
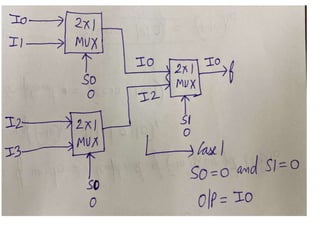
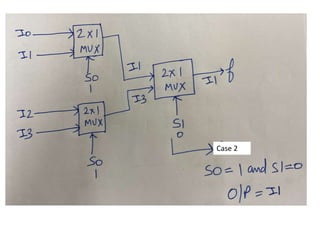
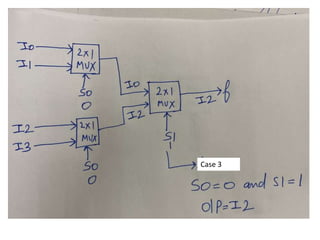
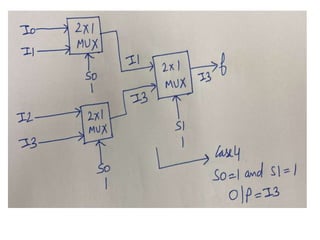
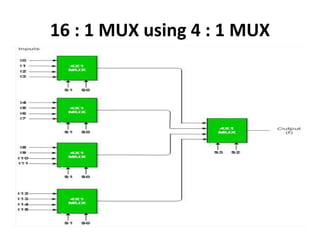
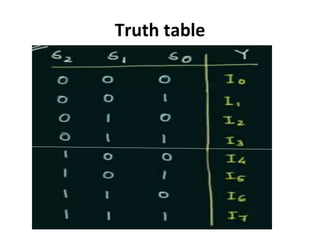
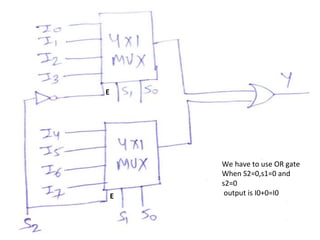
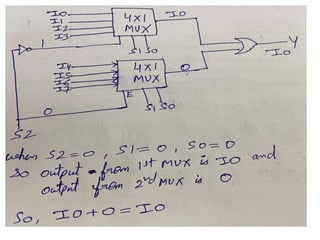
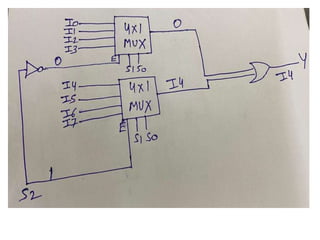
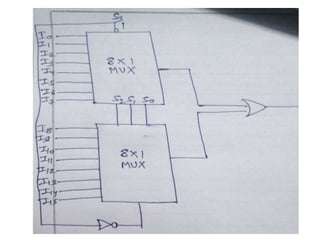
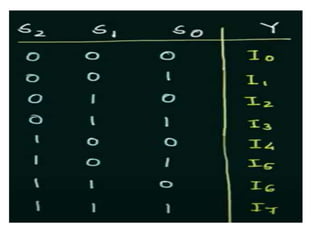
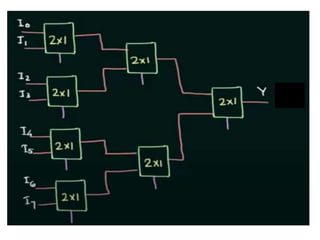
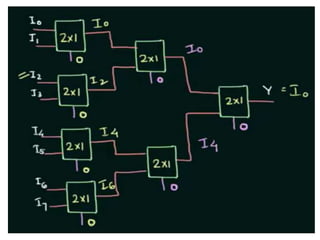
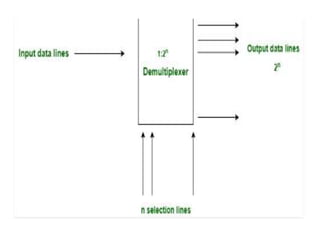
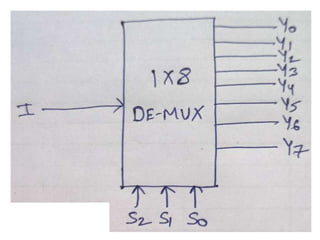
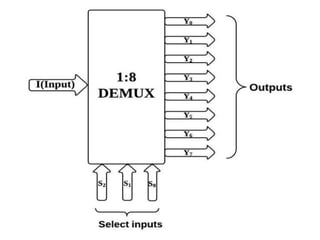
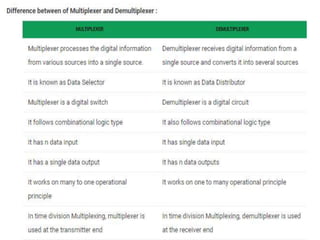
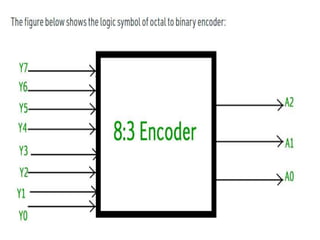
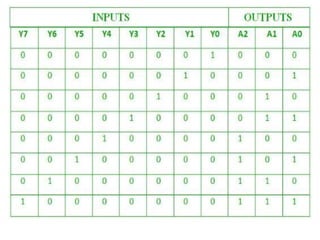
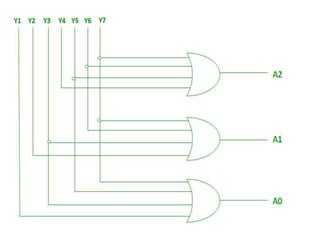
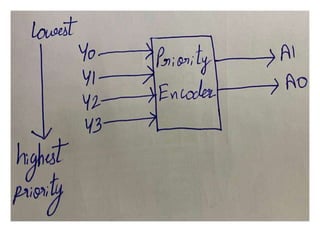
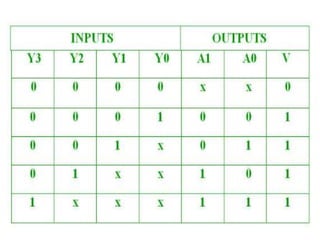
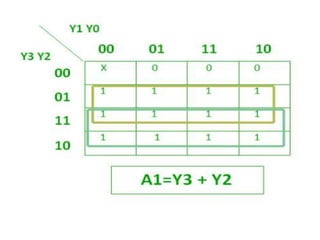
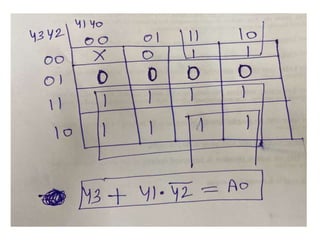
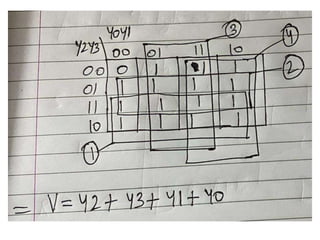
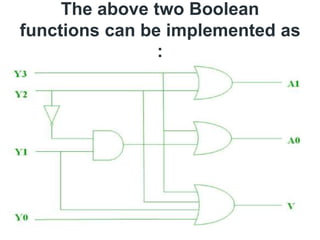
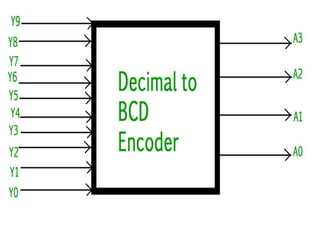
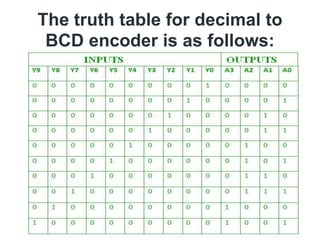
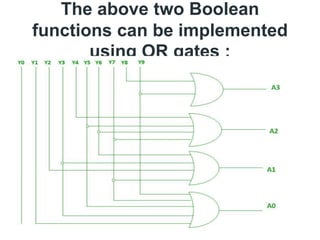
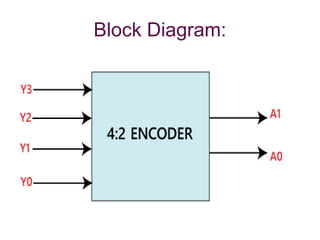
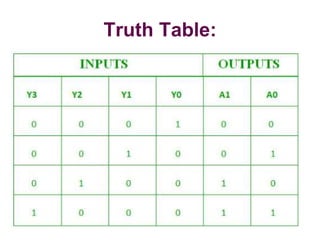
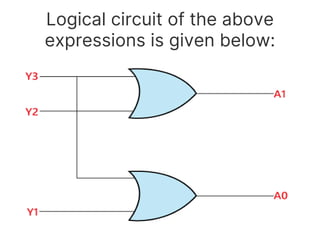
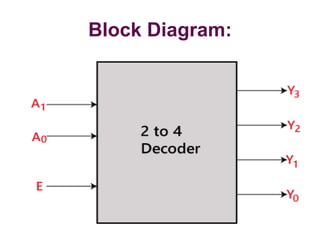
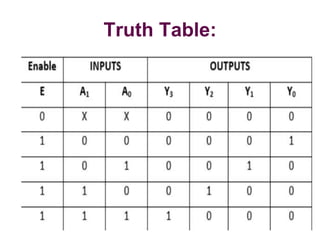
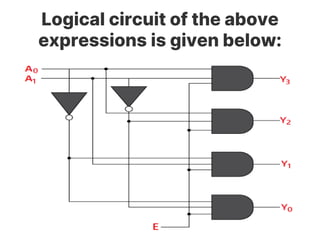
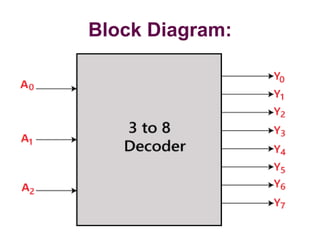
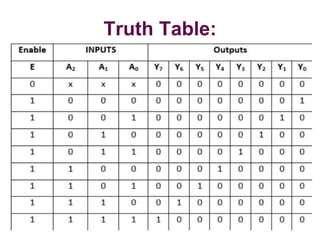
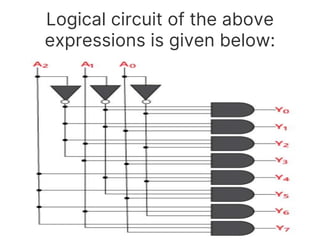
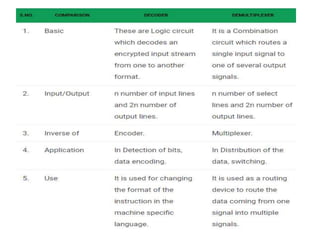
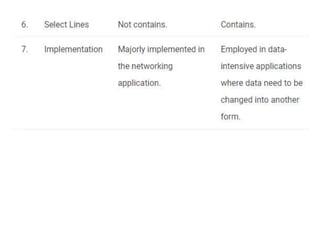
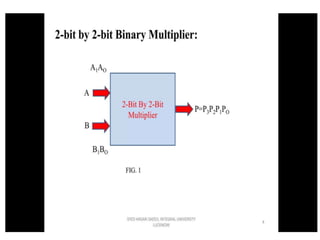
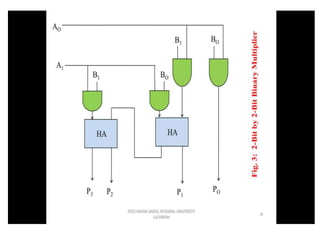
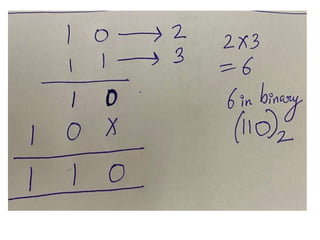
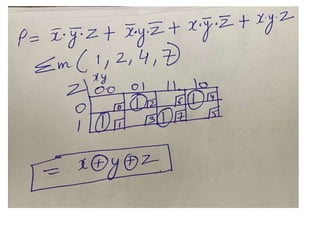
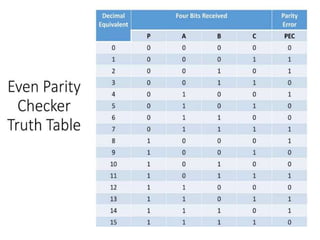
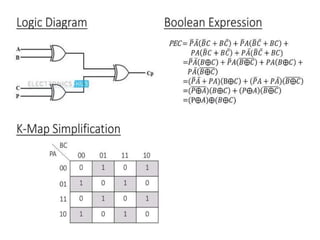
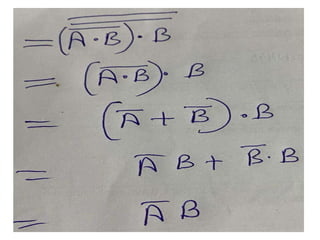The document discusses various digital logic circuits including half adders, full adders, parallel adders, subtractors, multiplexers, demultiplexers, encoders, and decoders. It explains the basic concepts and provides examples of implementing 1-bit, 2-bit, 4-bit, and 8-bit versions of these circuits using logic gates like AND, OR, and NOT. Implementation of higher order multiplexers and decoders using lower order building blocks is also covered.

1. Unit 2

6. Half Adder
• The addition of 2bits is called Half adder the
input variables are augent and addent bits
and output variables are sum&carry bits.
• A and B are the two input bits

9. 2018
Implement half adder circuit using NAND gate
only

11. Half Adder using NAND gates

13. Implementation of Half Adder using
NOR gates

14. Steps to derive half adder using NOR
• S=A XOR B
• C=A.B
C=(A’+B’)’=(A’)’.(B’)’=A.B

15. For Sum
S=A XOR B =A’B+AB’
We can write the same equation as
EX-NOR= (A’B’+AB)’=A’B+AB’
XOR’=EX-NOR

18. Half Subtractor
Half Subtractor (HS): Half subtractor is a combination circuit with
two inputs and two outputs which is difference and borrow. It
produces the difference between the two binary bits at the input
and also produces an output (Borrow) to indicate if a 1 has been
borrowed. In the subtraction (A-B), A is called a Minuend bit and
B is called as Subtrahend bit.

22. Implementation of Half Subtractor
using NAND gates

23. Steps to derive half subtractor using
NAND
D=A XOR B
B=A’.B
For D we require 4 NAND gate

24. Steps to derive half subtractor using
NAND
D=A XOR B
B=A’.B
For B
B=A’.B
We will have
((A.B)’.B)’
We will have
(((A.B)’.B)’)’

27. Implementation of Half Subtractor
using NOR gates

28. Steps to derive half subtractor using
NOR
D=A XOR B
B=A’.B
For D we require 5 NOR gate

29. Steps to derive half subtractor using
NOR
D=A XOR B
B=A’.B
For B (No extra gate is required)

30. Full Adder
• Full Adder is the adder which adds three
inputs and produces two outputs.
• The first two inputs are A and B and the third
input is an input carry as C-IN.
• The output carry is designated as C-OUT and
the normal output is designated as S which is
SUM.
• A full adder logic is designed in such a manner
that can take eight inputs together to create a
byte-wide adder and cascade the carry bit
from one adder to the another.

34. Logical Expression for SUM

35. Logical Expression for C-OUT:
Cin(A’B+AB’)+AB(Cin’+Cin)
Cin(A XOR B)+AB

39. Full Subtractor
• A full subtractor is a combinational
circuit that performs subtraction of two bits,
one is minuend and other is subtrahend,
taking into account borrow of the previous
adjacent lower minuend bit.
• This circuit has three inputs and two outputs.
The three inputs A, B and Bin, denote the
minuend, subtrahend, and previous borrow,
respectively.
• The two outputs, D and Bout represent the
difference and output borrow, respectively.

41. Truth Table

42. • From above table we can draw the K-Map as
shown for “difference” and “borrow”.
D=A XOR B XOR Bin

43. Logical expression for borrow

44. Logic Circuit for Full Subtractor

50. Method of 2’s Complement
Subtraction

51. Subtraction of Smaller Number from
Larger Number
• To subtract a smaller number from a larger
number using 2’s complement subtraction,
following steps are to be followed:
• Step-1: Determine the 2’s complement of the
smaller number
• Step-2: Add this to the larger number.
• Step-3: Omit the carry. Note that, there is
always a carry in this case

54. Subtraction of Larger Number
from Smaller Number
• To subtract a larger number from a smaller
number using 2’s complement subtraction,
following steps are to be followed:
• Step-1: Determine the 2’s complement of the
smaller number
• Step-2: Add this to the larger number.
• Step-3: There is no carry in this case. The
result is in 2’s complement form and is
negative.
• Step-4: To get answer in true form, take 2’s
complement and change its sign.

55. 1000 in decimal = 8
1010 in decimal = 12
8-12=-4
1010
1’s complement of 1010=0101
1’s complement+1=2’s complement
0101+1=0110

58. Parallel Adder
• A single full adder performs the addition of two one bit
numbers and an input carry.
• But a Parallel Adder is a digital circuit capable of
finding the arithmetic sum of two binary numbers that
is greater than one bit in length by operating on
corresponding pairs of bits in parallel.
• It consists of full adders connected in a chain where
the output carry from each full adder is connected to
the carry input of the next higher order full adder in
the chain.
• A n bit parallel adder requires n full adders to
perform the operation. So for the two-bit number,
two adders are needed while for four bit number, four
adders are needed and so on.

59. • Parallel adders normally incorporate carry
look a head logic to ensure that carry
propagation between subsequent stages of
addition does not limit addition speed

60. • As shown in the figure, firstly the full adder FA1
adds A1 and B1 along with the carry C1 to
generate the sum S1 (the first bit of the output
sum) and the carry C2 which is connected to the
next adder in chain.
• Next, the full adder FA2 uses this carry bit C2 to
add with the input bits A2 and B2 to generate the
sum S2(the second bit of the output sum) and the
carry C3 which is again further connected to the
next adder in chain and so on.
• The process continues till the last full adder FAn
uses the carry bit Cn to add with its input An and
Bn to generate the last bit of the output along
last carry bit Cout.

61. 2019
• Design a 4 bit parallel adder/subtractor with
controlled inverter and explain its working.
(6 marks)

62. Example
A = 0101
B= 1010
+___________
Sum = 1111
___________
Carry = 0

64. Parallel Subtractor
• A Parallel Subtractor is a digital circuit capable
of finding the arithmetic difference of two
binary numbers that is greater than one bit in
length by operating on corresponding pairs of
bits in parallel.
• The parallel subtractor can be designed in
several ways including combination of half
and full subtractors, all full subtractors or all
full adders with subtrahend complement
input.

67. • As shown in the figure, the parallel binary
subtractor is formed by combination of all full
adders with subtrahend complement input.
• This operation considers that the addition of
minuend along with the 2’s complement of the
subtrahend is equal to their subtraction.
• Firstly the 1’s complement of B is obtained by the
NOT gate and 1 can be added through the carry
to find out the 2’s complement of B. This is
further added to A to carry out the arithmetic
subtraction.
• The process continues till the last full adder FAn
uses the carry bit Cn to add with its input An and
2’s complement of Bn to generate the last bit of
the output along last carry bit Cout.

68. Example

69. Advantages of parallel Adder/Subtractor –
• The parallel adder/subtractor performs the
addition operation faster as compared to
serial adder/subtractor.
• Time required for addition does not depend
on the number of bits.
• The output is in parallel form i.e all the bits
are added/subtracted at the same time.
• It is less costly.

70. Disadvantages of parallel Adder/Subtractor –
• Each adder has to wait for the carry which is
to be generated from the previous adder in
chain.
• The propagation delay( delay associated with
the travelling of carry bit) is found to increase
with the increase in the number of bits to be
added.

71. Multiplexers

87. 2016
Explain 4:1 multiplexer with equation and
gates(5 marks)

91. • Now the implementation of 4:1 Multiplexer
using truth table and gates.

93. • Multiplexer can act as universal combinational
circuit.
• All the standard logic gates can be
implemented with multiplexers.

94. Implementation of Higher order MUX
using lower order MUX
1. 4 : 1 MUX using 2 : 1 MUX

98. Case 2

99. Case 2

100. Case 3

104. • In general, to implement B : 1 MUX using A : 1
MUX , one formula is used to implement the
same.
B / A = K1,
K1/ A = K2,
K2/ A = K3
• ………………
• KN-1 / A = KN = 1 (till we obtain 1 count of MUX).
• Example : 4:1 using 2:1 requires
4/2=2
2/2=1
2+1=3 MUX

105. 16 : 1 MUX using 4 : 1 MUX

106. • To implement 16: 1 MUX using 4 : 1 MUX
Using the above formula, we can obtain the
same.
16 / 4 = 4
4/ 4 = 1 (till we obtain 1 count of MUX)
Hence, total number of 4 : 1 MUX are required
to implement 16 : 1 MUX = 4 + 1 = 5.
• First level we need 4 MUX and second level
we need 1

107. Implementing 8X1 MUX using 4X1
MUX (Special Case)
• To implement 8: 1 MUX using 4 : 1 MUX
Using the above formula, we can obtain the
same.
8 / 4 = 2
2/ 4 = 0.5
• We cannot use 2.5 mux so we will use
different approach
• Using enable which will implement

108. Truth table

109. We have to use OR gate
When S2=0,s1=0 and
s2=0
output is I0+0=I0
E
E

113. How a 16:1 MUX can be designed
using two 8:1 MUX and one OR gate
S3 S2 S1 s0
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0

114. S3 S2 S1 s0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
How a 16:1 MUX can be designed
using two 8:1 MUX and one OR gate

115. Implementing 16X1 MUX using 8X1
MUX
• To implement 16: 1 MUX using 8 : 1 MUX
Using the above formula, we can obtain the
same.
16/8 = 2
2/ 8 = 0.5
• We cannot use 2.5 mux so we will use
different approach
• Using enable which will implement which will
enable and disable the circuit

117. Implementing 8X1 MUX using 2X1
MUX
• To implement 16: 1 MUX using 2 : 1 MUX
Using the above formula, we can obtain the
same.
8/ 2=4 (at level 1)
4/2=2 (at level 2)
2/2=1 (at level 3)
Total Number of multiplexer : 4+2+1=7

121. Demultiplexer
• Demultiplexer is a data distributor which
takes a single input and gives several outputs.
• In demultiplexer we have 1 input and
2n output lines where n is the selection line.

124. 2019
• Design a 1:8 DMUX circuit.

125. Design a 1:8 DMUX circuit

129. 2019
• What is encoder? Discuss the design of 8:3
(octal to binary encoder)

130. Encoders
• An Encoder is a combinational circuit that
performs the reverse operation of Decoder.
• It has maximum of 2^n input lines and ‘n’
output lines, hence it encodes the
information from 2^n inputs into an n-bit
code.
• It will produce a binary code equivalent to the
input, which is active High.
• Therefore, the encoder encodes 2^n input
lines with ‘n’ bits.

131. 8 : 3 Encoder (Octal to Binary) –
• The 8 to 3 Encoder or octal to Binary
encoder consists of 8 inputs : Y7 to Y0
and 3 outputs : A2, A1 & A0.
• Each input line corresponds to each octal
digit and three outputs generate
corresponding binary code

134. The above three Boolean functions A2, A1 and A0 can be implemented
using four input OR gates :

136. Priority Encoder
• A 4 to 2 priority encoder has 4 inputs : Y3,
Y2, Y1 & Y0 and 2 outputs : A1 & A0.
• Here, the input, Y3 has the highest
priority, whereas the input, Y0 has
the lowest priority.
• In this case, even if more than one input is
‘1’ at the same time, the output will be the
(binary) code corresponding to the input,
which is having higher priority

144. The above two Boolean
functions can be implemented as
:

145. Decimal to BCD Encoder
• The decimal to binary encoder usually
consists of 10 input lines and 4 output
lines.
• Each input line corresponds to the each
decimal digit and 4 outputs correspond to the
BCD code.
• This encoder accepts the decoded decimal
data as an input and encodes it to the BCD
output which is available on the output lines.
• The figure below shows the logic symbol of
decimal to BCD encoder :

147. The truth table for decimal to
BCD encoder is as follows:

148. Logical expression for A3, A2,
A1 and A0 :

149. The above two Boolean
functions can be implemented
using OR gates :

150. 4 to 2 line Encoder:
• In 4 to 2 line encoder, there are total of
four inputs, i.e., Y0, Y1, Y2, and Y3, and
two outputs, i.e., A0 and A1.
• In 4-input lines, one input-line is set to
true at a time to get the respective
binary code in the output side.
• Below are the block diagram and the
truth table of the 4 to 2 line encoder.

151. Block Diagram:

152. Truth Table:

153. The logical expression of the
term A0 and A1 is as follows

154. Logical circuit of the above
expressions is given below:

155. Binary Decoder
• A decoder is a combinational circuit that
converts binary information from n input
lines to a maximum of 2^n unique output
lines.

156. 2 to 4 line decoder:
• In the 2 to 4 line decoder, there is a total
of three inputs, i.e., A0, and A1 and E and
four outputs, i.e., Y0, Y1, Y2, and Y3.
• For each combination of inputs, when the
enable 'E' is set to 1, one of these four
outputs will be 1.
• The block diagram and the truth table of
the 2 to 4 line decoder are given below.

157. Block Diagram:

158. Truth Table:

159. The logical expression of the
term Y0, Y1, Y2, and Y3 is as
follows:

160. Logical circuit of the above
expressions is given below:

161. 3 to 8 line decoder:
• The 3 to 8 line decoder is also known
as Binary to Octal Decoder. In a 3 to 8
line decoder, there is a total of eight
outputs, i.e., Y0, Y1, Y2, Y3, Y4, Y5, Y6, and
Y7 and three inputs, i.e., A0, A1, and A2.
• This circuit has an enable input 'E'. Just
like 2 to 4 line decoder, when enable 'E' is
set to 1, one of these four outputs will be
1.
• The block diagram and the truth table of
the 3 to 8 line encoder are given below.

162. Block Diagram:

163. Truth Table:

165. Logical circuit of the above
expressions is given below:

176. 2017
• Draw the logic diagram of parity checker and
generator/checker. Explain its operation with
the help of truth table.(6.5 marks)

185. Parity Checker
• There are two types of parity checkers based
on the type of parity has to be checked.
• Even parity checker checks error in the
transmitted data, which contains message bits
along with even parity.
• Similarly, odd parity checker checks error in
the transmitted data, which contains message
bits along with odd parity.

186. 2018
Explain even parity and odd parity. Design a
circuit for even parity generator for 3 bit
message.(5.5 marks)