Документ представляет собой методическое пособие для учителей математики, посвященное теме уравнений и неравенств. Он включает в себя цели, задачи и содержание курса, а также советы по подготовке учащихся к государственной итоговой аттестации. Пособие также содержит методические рекомендации по организации уроков и материал для самостоятельной работы с нестандартными задачами.

1. УПРАВЛЕНИЕ ОБРАЗОВАНИЯ
АДМИНИСТРАЦИИ ГОРОДА МАКЕЕВКИ
МАКЕЕВСКИЙ УЧЕБНО-МЕТОДИЧЕСКИЙ ЦЕНТР
МАКЕЕВСКИЙ ЛИЦЕЙ №2 «ПРЕСТИЖ»
В МИРЕ УРАВНЕНИЙ И НЕРАВЕНСТВ
Методическое пособие для учителей

2. 4
УПРАВЛЕНИЕ ОБРАЗОВАНИЯ
АДМИНИСТРАЦИИ ГОРОДА МАКЕЕВКИ
МАКЕЕВСКИЙ УЧЕБНО-МЕТОДИЧЕСКИЙ ЦЕНТР
МАКЕЕВСКИЙ ЛИЦЕЙ №2 «ПРЕСТИЖ»
В МИРЕ УРАВНЕНИЙ И НЕРАВЕНСТВ
Методическое пособие для учителей
2015

3. 5
В мире уравнений и неравенств. Методическое пособие для учителей.
И.Н. Сапрыкина – Макеевка. Макеевский лицей №2 «Престиж». 2015 – 32 с.
Одобрено научно-методическим советом Макеевского учебно-
методического центра (Протокол № 4 (28) от 28.08.2015)
Предлагаемое пособие содержит материал к подготовке поурочных
планов к урокам по теме «Уравнения. Неравенства»
Пособие интересно образцами рассуждений, примерами выполнения
заданий
Пособие предназначено для учителей математики.

4. 6
ОГЛАВЛЕНИЕ
1. Пояснительная записка………………………………………………6
2. Решение задач с использованием свойств функции……………….9
3. О решении текстовых задач по математике………………………..25
4. Литература……………………………………………………………34

5. 7
Пояснительная записка
Материалы государственной итоговой аттестации, проведённой в 2014-
2015 учебном году, содержали уравнения и неравенства, методы, решения
которых не рассматриваются в основном курсе обучения математике.
Способов решения уравнений множество, и выпускник базовой и полной
средней школы должен владеть значительным их количеством. Предлагаю
своим коллегам при подготовке к ГИА распределить материал для
повторения либо как индивидуальные занятия, либо за счёт уроков
повторения.
Курс "В мире уравнений и неравенств" направлен на углубленное
изучение отдельных разделов основного курса математики и
предусматривает изучение нестандартных методов решения, а также
составления задач путем применения исследовательской деятельности.
Программа курса основывается преимущественно на методах активного
обучения (творческих, исследовательских, проектных), предусматривает
полноту и завершенность содержательных линий.
Цель курса:
Сформировать у учащихся навыки решения заданий повышенной
сложности:
 уравнения высших степеней разными способами (умение выбрать
наиболее рациональный из них);
 уравнений и неравенств, содержащих модули;
 уравнений и неравенств, содержащих радикалы;
 уравнений и неравенств, содержащих параметры;
 искусственные приемы решения уравнений.
Задачи курса:
 интеграция знаний по разнообразию методов решения уравнений
и неравенств;
 помощь в самоопределении учащихся путем погружения в
ситуацию самостоятельного выбора индивидуальной образовательной
траектории;
 активизация познавательной деятельности школьников;
 повышение информационной и коммуникативной
компетентности учащихся;
 поощрение самостоятельной работы учащихся с научной
литературой;

6. 8
 обеспечение педагогических условий для расцвета личности
школьника, его творческого потенциала;
 подготовка к успешной сдаче ГИА по математике.
Требования к уровню подготовленности учащихся:
В результате изучения курса учащиеся должны уметь:
 решать нестандартные уравнения и неравенства, используя
специальные математические методы;
 решать сюжетные задачи;
 производить прикидку и оценку результатов вычислений;
 при вычислениях сочетать устные и письменные приемы,
использовать приемы, рационализирующие вычисления;
 работать с различными источниками информаций;
 обосновывать свою точку зрения;
 демонстрировать личные достижения.
План курса
№ Наименование тем курса Количество
часов
1Алгебраические уравнения и неравенства 6
2Уравнения и неравенства, содержащие радикалы, степени,
модули
6
3Способ замены неизвестных при решении уравнений 6
4Решение уравнений и неравенств с использованием свойств,
входящих в них функций
6
5Текстовые задачи алгебры и их решение с помощью
уравнений и неравенств
6
6Творческая мастерская 4
ВСЕГО: 34 часа

7. 9
Содержание курса
ТЕМА 1. Алгебраические уравнения и неравенства (6ч)
Решение уравнений и неравенств с использованием разложения на
множители. Числа Ферма.
Метод неопределенных коэффициентов при решении алгебраических
уравнений.
Метод введения параметров.
Комбинирование различных способов решения. Неопределенные
уравнения.
Уравнения четвертой степени с дополнительными условиями.
Некоторые искусственные способы решения алгебраических уравнений:
 угадывание корня уравнения с последующим обоснованием;
 использование симметричности уравнений;
 использование суперпозиции функции;
 исследование уравнений на промежутках действительной оси.
Решение алгебраических неравенств. Обобщенный метод интервалов.
ТЕМА 2. Уравнения и неравенства, содержащие радикалы, степени,
модули (6ч)
Решение уравнений и неравенств, содержащих неизвестную под знаком
корня. Возведение в степень.
Умножение уравнения или неравенства на функцию.
Решение уравнений, содержащих несколько модулей. Использование
свойств абсолютной величины.
ТЕМА 3. Способ замены неизвестных при решении уравнений (6ч)
Решение рациональных уравнений методом замены неизвестных.
Решение дробно - рациональных уравнений разных видов методом
замены неизвестного.
Решение иррациональных уравнений различных видов разными
способами.
Метод сведения решения иррациональных уравнений к решению
тригонометрического уравнения.
Решение некоторых уравнений сведением их к решению систем
уравнений относительно новых неизвестных.
ТЕМА 4. Решение уравнений и неравенств с использованием
свойств, входящих в них функций (6ч)

8. 10
Использование ограниченности функции при решении уравнений и
неравенств.
Использование свойств синуса и косинуса при решении
тригонометрических уравнений.
Использование числовых неравенств при решении уравнений.
Применение производной. Использование монотонности функции при
решении уравнений и неравенств. Использование наибольшего и
наименьшего значений функции.
Применение теоремы Лагранжа для решения нестандартных уравнений
и неравенств.
ТЕМА 5. Текстовые задачи алгебры и их решение с помощью
уравнений и неравенств (6ч).
Решение задач на:
 дроби и проценты;
 смеси и сплавы;
 движение;
 работу;
 арифметическую и геометрическую прогрессии;
 числа.
Итоговый тест.
ТЕМА 6. Творческая мастерская.
Составление и решение заданий по всему курсу.
Работа над итоговым проектом.
Индивидуальные и групповые консультации по темам проектов.
Защита проектов.
РЕШЕНИЕ ЗАДАЧ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ
ФУНКЦИИ
Не всякое уравнение f(x) = g(x) или неравенство в результате
преобразований или с помощью удачной замены переменной может быть
сведено к уравнению или неравенству того или иного стандартного вида, для
которого существует определенный алгоритм решения. В таких случаях
иногда оказывается полезным использовать некоторые свойства функций,
такие как монотонность, периодичность, ограниченность, четность и др.
2.1 Использование монотонности функции

9. 11
Функция f (x) называется возрастающей на промежутке D, если для
любых чисел x1 и x2 из промежутка D таких, что x1 < x2 , выполняется
неравенство f (x1 ) < f (x2 ).
Функция f (x) называется убывающей на промежутке D, если для любых
чисел x1 и x2 из промежутка D таких, что x1 < x2 , выполняется неравенство f
(x1 ) > f (x2 ).
На показанном на рисунке 1 графике
Рисунок 1
Функция y = f (x), , возрастает на каждом из промежутков [a; x1 )
и (x2 ; b] и убывает на промежутке (x1 ; x2 ). Обратите внимание, что функция
возрастает на каждом из промежутков [a; x1 ) и (x2 ; b], но не на объединении
промежутков
Если функция возрастает или убывает на некотором промежутке, то она
называется монотонной на этом промежутке.
Заметим, что если f – монотонная функция на промежутке D (f (x)), то
уравнение f (x) = const не может иметь более одного корня на этом
промежутке.
Действительно, если x1 < x2 – корни этого уравнения на промежутке D
(f(x)), то f (x1 ) = f (x2 ) = 0, что противоречит условию монотонности.
Перечислим свойства монотонных функций (предполагается, что все
функции определены на некотором промежутке D).
· Сумма нескольких возрастающих функций является возрастающей
функцией.

10. 12
· Произведение неотрицательных возрастающих функций есть
возрастающая функция.
· Если функция f возрастает, то функции cf (c > 0) и f + c также
возрастают, а функция cf (c < 0) убывает. Здесь c – некоторая константа.
· Если функция f возрастает и сохраняет знак, то функция убывает.
· Если функция f возрастает и неотрицательна, то fn
где n N, также
возрастает.
· Если функция f возрастает и n – нечетное число, то f также возрастает.
· Композиция g (f (x)) возрастающих функций f и g также возрастает.
Аналогичные утверждения можно сформулировать и для убывающей
функции.
Точка a называется точкой максимума функции f, если существует такая
ε-окрестность точки a, что для любого x из этой окрестности выполняется
неравенство f (a) ≥ f (x).
Точка a называется точкой минимума функции f, если существует такая
ε-окрестность точки a, что для любого x из этой окрестности выполняется
неравенство f (a) ≤ f (x).
Точки, в которых достигается максимум или минимум функции,
называются точками экстремума.
В точке экстремума происходит смена характера монотонности
функции. Так, слева от точки экстремума функция может возрастать, а
справа – убывать. Согласно определению, точка экстремума должна быть
внутренней точкой области определения.
Если для любого (x ≠ a) выполняется неравенство f (x) ≤ f (a) ,
то точка a называется точкой наибольшего значения функции на множестве
D:
Если для любого (x ≠ b) выполняется неравенство f (x) > f (b)
, то точка b называется точкой наименьшего значения функции на множестве
D.
Точка наибольшего или наименьшего значения функции на множестве D
может быть экстремумом функции, но не обязательно им является.
Точку наибольшего (наименьшего) значения непрерывной на отрезке
функции следует искать среди экстремумов этой функции и ее значений на
концах отрезка.

11. 13
Решение уравнений и неравенств с использованием свойства
монотонности основывается на следующих утверждениях.
1. Пусть f(х) — непрерывная и строго монотонная функция на
промежутке Т , тогда уравнение f(x) = С, где С — данная константа, может
иметь не более одного решения на промежутке Т.
2. Пусть f(x) и g(х) — непрерывные на промежутке T функции, f(x)
строго возрастает, а g(х) строго убывает на этом промежутке, тогда
уравнение f(х) = =g(х) может иметь не более одного решения на промежутке
Т. Отметим, что в качестве промежутка T могут быть бесконечный
промежуток (-∞;+∞) , промежутки (а;+∞), (-∞; а), [а;+∞), (-∞; b], отрезки,
интервалы и полуинтервалы.
Пример 2.1.1 Решите уравнение
. [28] (1)
Решение. Очевидно, что х ≤ 0 не может являться решением данного
уравнения, так как тогда . Для х > 0 функция
непрерывна и строго возрастает, как произведение двух непрерывных
положительных строго возрастающих для этих х функций f(x) = х
и . Значит, в области х > 0 функция принимает
каждое свое значение ровно в одной точке. Легко видеть, что х = 1 является
решением данного уравнения, следовательно, это его единственное решение.
Ответ: {1}.
Пример 2.1.2 Решите неравенство
. (2)
Решение. Каждая из функций у = 2x
, у = 3x
, у = 4х
непрерывная и строго
возрастающая на всей оси. Значит, такой же является и исходная
функция . Легко видеть, что при х = 0 функция
принимает значение 3. В силу непрерывности и строгой монотонности этой
функции при х > 0 имеем , при х < 0 имеем .
Следовательно, решениями данного неравенства являются все х < 0.
Ответ: (-∞; 0).
Пример 2.1.3 Решите уравнение
. (3)

12. 14
Решение. Область допустимых значений уравнения (3) есть
промежуток . На ОДЗ функции и
непрерывны и строго убывают, следовательно, непрерывна и убывает
функция . Поэтому каждое свое значение функция h(x)
принимает только в одной точке. Так как , то х = 2 является
единственным корнем исходного уравнения.
Ответ: {2}.
2.2 Использование ограниченности функции
При решении уравнений и неравенств свойство ограниченности снизу
или сверху функции на некотором множестве часто играет определяющую
роль.
Если существует число C такое, что для любого выполняется
неравенство f (x) ≤ C, то функция f называется ограниченной сверху на
множестве D (рисунок 2).
Рисунок 2
Если существует число c такое, что для любого выполняется
неравенство f (x) ≥ c, то функция f называется ограниченной снизу на
множестве D (рисунок 3).

13. 15
Рисунок 3
Функция, ограниченная и сверху, и снизу, называется ограниченной на
множестве D. Геометрически ограниченность функции f на множестве D
означает, что график функции y = f (x), лежит в полосе c ≤ y ≤ C
(рисунок 4).
Рисунок 4
Если функция не является ограниченной на множестве, то говорят, что
она не ограничена.
Примером функции, ограниченной снизу на всей числовой оси, является
функция y = x2
. Примером функции, ограниченной сверху на множестве (–∞;

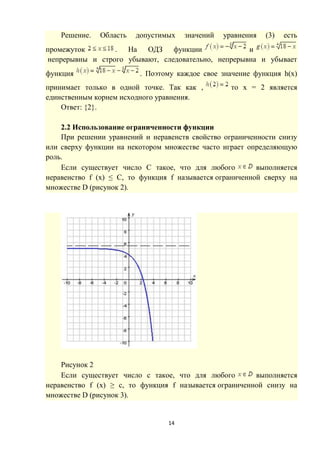
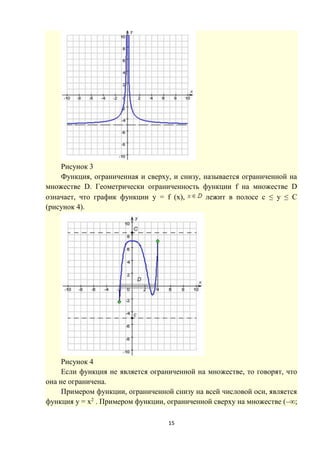
14. 16
0) является функция y = 1/x. Примером функции, ограниченной на всей
числовой оси, является функция y = sin x.
Пример 2.2.1 Решите уравнение
sin(x3
+ 2х2
+ 1) = х2
+ 2х + 2. (4)
Решение. Для любого действительного числа х имеем sin(x3
+ 2х2
+ 1) ≤
1, х2
+ 2х + 2 = (x + 1)2
+1 ≥ 1. Поскольку для любого значения х левая часть
уравнения не превосходит единицы, а правая часть всегда не меньше
единицы, то данное уравнение может иметь решение только при .
При , , т.е. при уравнение
(4) так же корней не имеет .
Ответ: Ø.
Пример 2.2.2 Решите уравнение
. (5)
Решение. Очевидно, что х = 0, х = 1, х = -1 являются решениями данного
уравнения. Для нахождения других решений в силу нечетности функции f(х)
= = x3
- x - sinπx достаточно найти его решения в области х > 0, х ≠ 1,
поскольку если x0 > 0 является его решением, то и (-x0 ) также является его
решением.
Разобьем множество х > 0, х ≠ 1, на два промежутка: (0; 1) и (1; +∞)
Перепишем начальное уравнение в виде x3
- x = sinπx. На промежутке (0;
1) функция g(х) = x3
- x принимает только отрицательные значения,
поскольку х3
< < х, а функция h(x) = sinπx только положительные.
Следовательно, на этом промежутке уравнение не имеет решений.
Пусть х принадлежит промежутку (1; +∞). Для каждого из таких
значений х функция g(х) = х3
- х принимает положительные значения,
функция h(x) = sinπxпринимает значения разных знаков, причем на
промежутке (1; 2] функция h(x) = sinπx неположительна. Следовательно, на
промежутке (1; 2] уравнение решений не имеет.
Если же х > 2, то |sinπx| ≤ 1, x3
- x = x(x2
- 1) > 2∙3 = 6, а это означает, что
и на промежутке (1; +∞) уравнение также не имеет решений.
Итак, x = 0, x = 1 и x = -1 и только они являются решениями исходного
уравнения.
Ответ: {-1; 0; 1}.
Пример 2.2.3 Решите неравенство

15. 17
. (6)
Решение. ОДЗ неравенства есть все действительные x, кроме x = -1.
Разобьем ОДЗ неравенства на три множества: -∞ < x < -1, -1 < x ≤ 0, 0 < x <
+∞ и рассмотрим неравенство на каждом из этих промежутков.
Пусть -∞ < x < -1. Для каждого из этих x имеем g(x) = < 0, а f(x) =
2x
> 0. Следовательно, все эти x являются решениями неравенства.
Пусть -1 < x ≤ 0. Для каждого из этих x имеем g(x) = 1 - , а f(x) =
2x
≤ 1. Следовательно, ни одно из этих x не является решением данного
неравенства.
Пусть 0 < x < +∞. Для каждого из этих x имеем g(x) = 1 - ,
a . Следовательно, все эти x являются решениями исходного
неравенства.
Ответ: .
2.3 Использование периодичности функции
Функция f (x) называется периодической с периодом T ≠ 0, если
выполняются два условия:
· если , то x + T и x – T также принадлежат области определения D
(f (x));
· для любого выполнено равенство
f (x + T) = f (x).
Поскольку то из приведенного определения следует, что
Если T – период функции f (x), то очевидно, что каждое число nT,
где , n ≠ 0, также является периодом этой функции.
Наименьшим положительным периодом функции называется
наименьшее из положительных чисел T, являющихся периодом данной
функции.

16. 18
График периодической функции
График периодической функции обычно строят на промежутке [x0 ; x0 +
T), а затем повторяют на всю область определения.
Хорошим примером периодических функций могут служить
тригонометрические функции y = sin x, y = cos x (период этих функций равен
2π), y = tg x (период равен π) и другие. Функция y = const также является
периодической. Для нее периодом является любое число T ≠ 0.
В заключение отметим свойства периодических функций. [19]
· Если f (x) – периодическая функция с периодом T, то функция
g (x) = A · f (kx + b)
где k ≠ 0 также является периодической с периодом .
· Пусть функции f1 (x) и f2 (x) определены на всей числовой оси и
являются периодическими с периодами T1 > 0 и T2 > 0. Тогда если то
функция периодическая с периодом T, равным
наименьшему общему кратному чисел T1 и T2.
Пример 2.4.1 Функция периодическая с периодом T = 5. Известно,
что . Найдите

17. 19
Решение. Преобразуем отдельно каждое слагаемое:
Тогда
Ответ: 2.
Пример 2.4.2 [24] Найдите период функции
Решение. Преобразуем данное выражение:
имеет период ;
имеет период .
Тогда функция имеет период
Ответ: π.
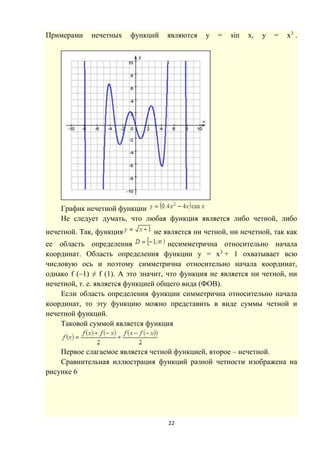
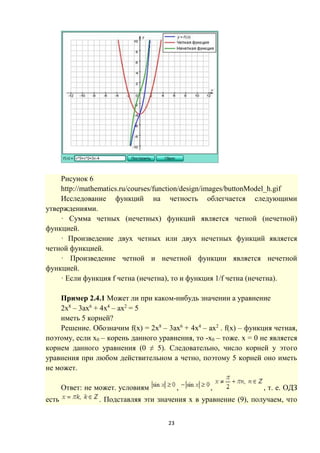
Пример 2.4.3 Пусть - периодическая функция с периодом 3 такая,
что
; .
Решите уравнение:
(7)
График функции на множестве [0;3) изображен на рисунке 3:

18. 20
Рисунок 5
Т.к. 3 - период функции , то , тогда
уравнение (7) примет вид , рассмотрим два случая.
1) пусть , т.е. , тогда уравнение примет вид:
, значит и значит
,
2) пусть то , тогда уравнение примет вид:
; итак
,

19. 21
т.е. , .
Ответ: .
2.4 Использование четности функции
Функция f (x) называется четной, если для любого выполняются
равенства:
1) ,
2) f (–x) = f (x).
График четной функции на всей области определения симметричен
относительно оси OY. Примерами четных функций могут служить y = cos x,
y = |x|, y = x2
+ |x|
График четной функции
Функция f (x) называется нечетной, если для любого выполняются
равенства:
1) ,
2) f (–x) = –f (x).
Иными словами функция называется нечетной, если ее график на всей
области определения симметричен относительно начала координат.

20. 22
Примерами нечетных функций являются y = sin x, y = x3
.
График нечетной функции
Не следует думать, что любая функция является либо четной, либо
нечетной. Так, функция не является ни четной, ни нечетной, так как
ее область определения несимметрична относительно начала
координат. Область определения функции y = x3
+ 1 охватывает всю
числовую ось и поэтому симметрична относительно начала координат,
однако f (–1) ≠ f (1). А это значит, что функция не является ни четной, ни
нечетной, т. е. является функцией общего вида (ФОВ).
Если область определения функции симметрична относительно начала
координат, то эту функцию можно представить в виде суммы четной и
нечетной функций.
Таковой суммой является функция
Первое слагаемое является четной функцией, второе – нечетной.
Сравнительная иллюстрация функций разной четности изображена на
рисунке 6

21. 23
Рисунок 6
http://mathematics.ru/courses/function/design/images/buttonModel_h.gif
Исследование функций на четность облегчается следующими
утверждениями.
· Сумма четных (нечетных) функций является четной (нечетной)
функцией.
· Произведение двух четных или двух нечетных функций является
четной функцией.
· Произведение четной и нечетной функции является нечетной
функцией.
· Если функция f четна (нечетна), то и функция 1/f четна (нечетна).
Пример 2.4.1 Может ли при каком-нибудь значении а уравнение
2x8
– 3аx6
+ 4x4
– аx2
= 5
иметь 5 корней?
Решение. Обозначим f(x) = 2х8
– 3ах6
+ 4х4
– ах2
. f(x) – функция четная,
поэтому, если x0 – корень данного уравнения, то -x0 – тоже. x = 0 не является
корнем данного уравнения (0 ≠ 5). Следовательно, число корней у этого
уравнения при любом действительном а четно, поэтому 5 корней оно иметь
не может.
Ответ: не может. условиям , , , т. е. ОДЗ
есть . Подставляя эти значения х в уравнение (9), получаем, что

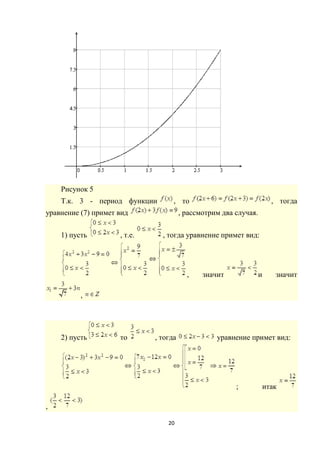
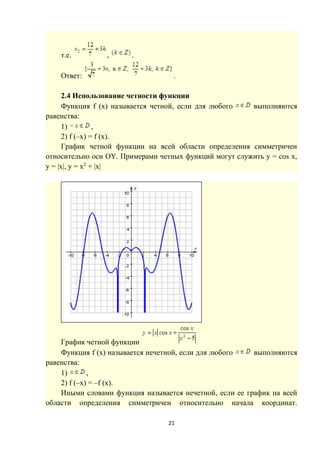
22. 24
его левая и правая части равны 0, а это означает, что все ,
являются его решениями.
Ответ:
Пример 2.5.3 Решите неравенство
. (10)
Решение. ОДЗ неравенства (10) есть все х, удовлетворяющие
условию . Ясно, что х = 1 не является решением неравенства (10). Для
х из промежутка имеем , а . Следовательно, все х из
промежутка являются решениями неравенства (10).
Ответ: .
Пример 2.5.4 [26] Решите неравенство
. (11)
Решение. ОДЗ неравенства (11) есть все х из промежутка .
Разобьем это множество на два промежутка и .
Для х из промежутка имеем , .
Следовательно, на этом промежутке, и поэтому
неравенство (11) не имеет решений на этом промежутке.
Пусть х принадлежит промежутку , тогда и .
Следовательно, для таких х, и, значит, на этом промежутке
неравенство (11) также не имеет решений.
Итак, неравенство (11) решений не имеет.
Ответ: Ø.
2.5 Использование ОДЗ функции
Область определения функции - это множество всех допустимых
действительных значений аргумента x (переменной x), при которых
функция определена. Область определения иногда еще называют
областью допустимых значений функции (ОДЗ). Для нахождения ОДЗ
функции нужно проанализировать данное соответствие и установить
встречающиеся запретные операции (деление на нуль, возведение в

23. 25
рациональную степень отрицательного числа, логарифмические операции
над отрицательными числами и т. п.).
Иногда знание ОДЗ позволяет доказать, что уравнение (или
неравенство) не имеет решений, а иногда позволяет найти решения
уравнения (или неравенства) непосредственной подстановкой чисел из ОДЗ.
Пример 2.5.1 Решите уравнение
. (8)
Решение. ОДЗ этого уравнения состоит из всех х, одновременно
удовлетворяющих условиям и , т. е. ОДЗ есть пустое
множество. Этим решение уравнения и завершается, так как установлено, что
ни одно число не может являться решением, т. е. что уравнение не имеет
корней.
Ответ: Ø.
Пример 2.5.2 Решите уравнение
. (9)
Решение. ОДЗ этого уравнения состоит из всех x, одновременно
удовлетворяющих условиям , , , т. е. ОДЗ
есть . Подставляя эти значения х в уравнение (9), получаем, что
его левая и правая части равны 0, а это означает, что все ,
являются его решениями.
Ответ:
Пример 2.5.3 Решите неравенство
. (10)
Решение. ОДЗ неравенства (10) есть все х, удовлетворяющие
условию . Ясно, что х = 1 не является решением неравенства (10). Для
х из промежутка имеем , а . Следовательно, все х из
промежутка являются решениями неравенства (10).
Ответ: .
Пример 2.5.4 [26] Решите неравенство
. (11)
Решение. ОДЗ неравенства (11) есть все х из промежутка .
Разобьем это множество на два промежутка и .

24. 26
Для х из промежутка имеем , .
Следовательно, на этом промежутке, и поэтому
неравенство (11) не имеет решений на этом промежутке.
Пусть х принадлежит промежутку , тогда и .
Следовательно, для таких х, и, значит, на этом промежутке
неравенство (11) также не имеет решений.
Итак, неравенство (11) решений не имеет.
Ответ: Ø.
О решении текстовых задач по математике
Одним из вопросов методики преподавания математики является вопрос
формирования у учащихся умений и навыков решения текстовых задач.
Задачи являются материалом для ознакомления учащихся с новыми
понятиями, для развития логического мышления, формирования
межпредметных связей. Задачи позволяют применять знания, полученные
при изучении математики, при решении вопросов, которые возникают в
жизни человека. Этапы решения задач являются формами развития
мыслительной деятельности.
Для решения текстовых задач применяются три основных метода:
арифметический, алгебраический и комбинированный. Рассмотрим каждый
из этих методов.
I. Арифметический метод.
Первым этапом решения задач арифметическим методом является
разбор условия задачи и составление плана её решения. Этот этап решения
задачи сопровождается максимальной мыслительной деятельностью.
Вторым этапом является решение задачи по составленному плану. Этот
этап решения проводится учащимися без особых затруднений и в
большинстве случаев носит тренировочный характер.
Третьим важным этапом решения задачи является проверка решения
задачи. Она проводится по условию задачи. Пренебрежение проверкой при
решении задачи, замена её проверкой ответов снижает роль решения задачи в
процессе развития логического мышления учащихся.
При решении текстовых задач арифметическим методом у учащихся
вырабатываются определённые умения и навыки, которые в процессе
дальнейшего обучения должны совершенствоваться и закрепляться.

25. 27
При арифметическом методе решения задач формируются 56 основных
умений и навыков. Из них 38 умений и навыков приобретаются при решении
задач как арифметическим, так и алгебраическим методами.
К ним относятся следующие умения и навыки:
1. Краткая запись условия задачи.
2. Изображение условия задачи с помощью рисунка.
3. Логические приёмы мышления: наблюдение и сравнение, анализ
и синтез, абстрагирование и конкретизация, обобщение и ограничение,
умозаключения индуктивного и дедуктивного характера и умозаключения
по аналогии.
4. Выполнение арифметических действий над величинами
(числами).
5. Изменение (увеличение или уменьшение) величины (числа) в
несколько раз
6. Нахождение разностного сравнения величин (чисел).
7. Нахождение кратного сравнения величин (чисел).
8. Использование свойств изменения результатов действий в
зависимости от изменения компонентов.
9. Изменение (увеличение или уменьшение) величины (числа) на
несколько единиц величины (числа).
10. Нахождение дроби от величины (числа).
11. Нахождение величины (числа) по данной её (его) дроби.
12. Нахождение процентов данной величины (данного числа).
13. Нахождение величины (числа) по её (его) проценту.
14. Нахождение процентного отношения двух величин (чисел).
15. Составление пропорций.
16. Понятие прямой и обратной пропорциональной зависимости
величин (чисел).
17. Понятие производительности труда.
18. Определение производительности труда при совместной работе.
19. Определение части работы, выполненной в течение некоторого
промежутка времени.
20. Определение скорости движения.
21. Определение пути, пройденного телом.
22. Определение времени движения тела.
23. Понятие о собственной скорости (скорости в стоячей воде)
движения тела по воде.

26. 28
24. Нахождение пути, пройденного двумя телами при встречном
движении.
25. Нахождение скорости движения тела по течению и против
течения реки.
26. Нахождение времени прохождения телом единицы пути при
заданной скорости движения.
27. Нахождение скорости сближения тел, движущихся в одном
направлении, и скорости удаления.
28. Нахождение скорости сближения или скорости удаления тел,
движущихся в противоположных направлениях или при встречном
движении.
29. Нахождение части пути, пройденного телом за определённое
время, когда известно время прохождения всего пути.
30. Нахождение количества вещества, содержащегося в растворе,
смеси, сплаве.
31. Нахождение концентрации, процентного содержания.
32. Нахождение стоимости товара, акции.
33. Нахождение цены товара, акции.
34. Нахождение прибыли.
35. Нахождение количества вредных веществ в воде, воздухе.
36. Нахождение себестоимости продукции.
37. Расчёт начислений банка на вклады.
38. Проверка решения задачи по условию.
Умения и навыки, которые формируются в процессе решения задач
только арифметическим методом, можно разбить на две группы. К первой
группе относятся умения и навыки, которые необходимы для дальнейшего
изучения математики.
К первой группе относятся следующие умения и навыки:
1. Перевод календарного времени в арифметическое число.
2. Перевод арифметического числа в календарное время.
3. Нахождение времени предыдущего события.
4. Нахождение времени последующего события.
5. Нахождение промежутка времени между двумя событиями.
Все умения и навыки этой группы формируются в процессе решения
задач на вычисление времени, т.е. тех задач, которые нет смысла решать
алгебраически.

27. 29
Вторая группа – это те умения и навыки, без знания которых можно
решить все текстовые задачи алгебраическим методом, и в дальнейшем их
незнание не будет пробелом в математическом образовании учащихся.
Ко второй группе относятся следующие умения и навыки:
1. Введение понятия "часть".
2. Выполнение действий сложения и вычитания частей.
3. Выполнение умножения и деления части на число.
4. Приём уравнивания большего числа с меньшим и меньшего с
большим.
5. Приём уравнивания прибавлением к меньшему числу и
вычитанием из большего числа их полуразности.
6. Определение числа частей, составляющих данное число.
7. Введение понятий условной единицы.
8. Нахождение дроби условной единицы и её частей.
9. Сравнение частей величин.
10. Сложение и вычитание частей единицы.
11. Метод исключения неизвестного посредством замены одной
величины другой.
12. Решение задач методом предположения.
13. Составление плана решения задачи.
Эти умения и навыки, несомненно, представляют интерес. Но почти все
из них можно отнести к числу умений и навыков, формирующихся у
учащихся при решении нестандартных задач. Решение таких задач следует
проводить систематически наряду с решением стандартных текстовых задач.
II. Алгебраический метод.
Под алгебраическим методом решения задач понимается такой метод
решения, когда неизвестные величины находятся в результате решения
уравнения или системы уравнений, решения неравенства или системы
неравенств, составленных по условию задачи. Иногда алгебраическое
решение задачи бывает очень сложным.
При решении задач алгебраическим методом основная мыслительная
деятельность сосредотачивается на первом этапе решения задачи: на разборе
условия задачи и составлении уравнений или неравенств по условию задачи.
Вторым этапом является решение составленного уравнения или системы
уравнений, неравенства или системы неравенств.
Третьим важным этапом решения задач является проверка решения
задачи, которая проводится по условию задачи.

28. 30
При алгебраическом методе решения формируются 55 основных умений
и навыков.
Отличными от тех, которые формируются при арифметическом их
решении, являются следующие:
1. Введение неизвестного.
2. Введение двух неизвестных.
3. Введение трёх и более неизвестных.
4. Выполнение действий сложения и вычитания неизвестных.
5. Выполнение действий умножения и деления неизвестных.
6. Запись зависимости между величинами с помощью букв и чисел.
7. Решение линейных уравнений.
8. Решение линейных неравенств.
9. Решение квадратных уравнений и неравенств.
10. Решение дробно-рациональных уравнений и неравенств.
11. Решение систем уравнений и систем неравенств.
12. Составление одного уравнения (неравенства) с двумя
неизвестными.
13. Решение уравнения (неравенства) с двумя неизвестными.
14. Выбор значений неизвестных по условию задачи.
15. Составление уравнений с параметром по условию текстовой
задачи.
16. Решение уравнений с параметром.
17. Исследовательская работа.
В связи с внедрением в школьную программу элементов высшей
математики, с ускоренным развитием и внедрением во все сферы
вычислительной математики большое значение имеет формирование у
учащихся не отдельных специфических навыков, а тех умений и навыков,
которые имеют дальнейшее приложение. К числу этих умений и навыков
относятся умения и навыки, которые формируются в процессе решения задач
алгебраическим методом.
III. Комбинированный метод.
Этот метод получается в результате включения в алгебраический метод
решения задач решение, в котором часть неизвестных величин определяется
с помощью решения уравнения или системы уравнений, неравенств или
систем неравенств, а другая часть – арифметическим методом. В этом случае
решение текстовых задач значительно упрощается.

29. 31
При решении текстовых задач учащимся могут помочь несколько
простых и общих советов, а также приведённые ниже примеры решения
задач.
Совет 1. Не просто прочитайте, а тщательно изучите условие задачи.
Попытайтесь полученную информацию представить в другом виде – это
может быть рисунок, таблица или просто краткая запись условия задачи.
Совет 2. Выбор неизвестных.
В задачах "на движение" – это обычно скорость, время, путь. В задачах
“на работу” - производительность и т.д.
Не надо бояться большого количества неизвестных или уравнений.
Главное, чтобы они соответствовали условию задачи и можно было
составить соответствующую “математическую модель” (уравнение,
неравенство, система уравнений или неравенств).
Совет 3. Составление и решение “математической модели”.
При составлении “математической модели” (уравнения, неравенства,
системы уравнений или неравенств) ещё раз внимательно прочитайте
условие задачи. Проследите за тем, что соответствует каждой фразе текста
задачи в полученной математической записи и чему в тексте задачи
соответствует каждый “знак” полученной записи (сами неизвестные,
действия над ними, полученные уравнения, неравенства или их системы).
Очень важно не только составить уравнение, неравенство, систему
уравнений или неравенств, но и решить составленное.
Если решение задачи не получается, то нужно ещё раз прочитать и
проанализировать задачу (заданный текст и полученную запись).
Иногда по условию задачи достаточно отыскать не сами неизвестные, а
их комбинации. Например, не x и y, а x+y, x/y, 1/x и т.п.
Если кажется, что получилось правильное, но очень сложное
выражение, то попробуйте ввести другие неизвестные, может быть, изменив
их количество, чтобы получилась более простая модель.
Иногда неизвестные в задачах выражаются только целыми числами,
тогда при решении задач нужно использовать свойства целых чисел.
Совет 4. Решение сложной текстовой задачи – процесс творческий.
Иной раз требуется вернуться к самому началу задачи, учитывая и
анализируя уже полученные результаты.
При решении задач короткую запись задачи можно сделать с помощью
рисунка или таблицы.
Таблица является универсальным средством и позволяет решать
большое количество идейно близких задач.

30. 32
Можно выделить семь вопросов, которые дают верное направление
решению задач разных типов.
Вопросы к задаче с комментариями к ним:
1. О каком процессе идёт речь? Какими величинами
характеризуется этот процесс? (Количество величин соответствует числу
столбцов таблицы).
2. Сколько процессов в задаче? (Количество процессов
соответствует числу строк в таблице).
3. Какие величины известны? Что надо найти? (Таблица
заполняется данными задачи; ставится знак вопроса).
4. Как связаны величины в задаче? (Вписать основные формулы,
выяснить связи и соотношения величин в таблице).
5. Какую величину (величины) удобно выбрать в качестве
неизвестной или неизвестных? (Клетки в таблице заполняются в
соответствии с выбранными неизвестными).
6. Какие условия используются для составления “модели”?
(Выписать полученную “модель”)
7. Легко ли решить полученное? (Если решить сложно, ввести
новые переменные, использовать другие соотношения).
Пример решения задачи.
Задача. Расстояние между двумя городами скорый поезд проходит на 4
часа быстрее товарного и на 1 час быстрее пассажирского. Найти скорости
товарного и скорого поездов, если известно, что скорость товарного поезда
составляет 5/8 от скорости пассажирского и на 50 км/ч меньше скорости
скорого.
Решение (черновик).
Отвечаем на вопросы, поэтапно составляя таблицу.
1. Речь идёт о процессе движения, которое характеризуется тремя
величинами: расстояние, скорость, время (3 столбца таблицы).
2. В задаче 3 процесса: движение скорого, пассажирского и товарного
поездов (3 строчки таблицы).
Можно составить “скелет” таблицы.
Величины
Процессы
Расстояние (км) Скорость (км/ч) Время (ч)
Скорый поезд с с с
Пассажирский с с с

31. 33
поезд
Товарный поезд с с с
3. Заполняем таблицу в соответствии с условиями задачи
4. Вводим неизвестные величины: x, км/ч – скорость товарного поезда, y,
ч – время движения скорого поезда.
5. Составим “модель”.
(x+50)y = 8/5 x(y+1)
8/5 x(y+1) = x(y+4)
6. Решаем эту систему. Из первого уравнения находим у. Из второго
уравнения находим х.
Решение задачи (чистовик).
Пусть х, км/ч – скорость товарного поезда (х>0), у, ч – время движения
скорого поезда (у>0).
Составляем таблицу.
Величины
Процессы
Расстояние
(км)
Скорость
(км/ч)
Время (ч)
Скорый поезд (х+50)у х+50 ?
у
Пассажирски
й поезд
8/5 х(у+1) 8/5 х у+1
Товарный
поезд
х(у+4) х ?
у+4
По условию задачи поезда прошли одно и то же расстояние. Получаем
систему уравнений
8/5 х(у+1) = х(у+4)
(х+50)у = х(у+4).
По условию задачи х>0, тогда
8(у+1) = 5(у+4)
(х+50)у = х(у+4),
3у = 12
(х+50)у = х(у+4),
у = 4
х+50 = 2х,
у = 4
х = 50.
Полученные значения неизвестных удовлетворяют условию х>0, у>0,
значит удовлетворяют условию задачи.

32. 34
50 км/ч – скорость товарного поезда.
50+50 = 100 (км/ч) – скорость скорого поезда.
Проверка по условию задачи.
50 км/ч – скорость товарного поезда,
4+4 = 8 (ч) – время движения товарного поезда.
50*8 = 400 (км) – расстояние, которое прошёл товарный поезд.
50*8/5 = 80 (км/ч) – скорость пассажирского поезда.
4+1 = 5 (ч) – время движения пассажирского поезда.
80*5 = 400 (км) – расстояние, которое прошёл пассажирский поезд.
4 ч – время движения скорого поезда.
50+50 = 100 (км/ч) – скорость скорого поезда.
100*4 = 400 (км) – расстояние, которое прошёл скорый поезд.
Каждый поезд прошёл одно и то же расстояние.
Задача решена верно.
Ответ: 50 км/ч, 100 км/ч.
Аналогично можно решать задачи “на работу”, “наполнение бассейна”.
Решение текстовых задач способствует, с одной стороны, закреплению
на практике приобретённых умений и навыков, с другой стороны, развитию
логического мышления учащихся.
Наблюдается активизация их мыслительной деятельности работы. При
правильной организации работы у учащихся развивается активность,
наблюдательность, находчивость, сообразительность, смекалка, развивается
абстрактное мышление, умение применять теорию к решению конкретных
задач.

33. 35
Литература.
1. Виленкин Н.Я. и др. За страницами учебника математики:
Арифметика. Алгебра. Геометрия: Кн. Для учащихся 10-11 кл.
общеобразоват. учреждений. - М.: Просвещение: АО "Учеб. лит.", 1996.
2. Высоцкий И.Р. и др. Единый государственный экзамен 2010.
Универсальные материалы для подготовки учащихся (ФИПИ-М.: Интеллект-
Центр, 2010) .
3. Водинчар М.И. и др. Решение задач на смеси, растворы и сплавы
методом уравнений. Математика в школе 2001г № 4.
4. Кац М. Проценты. Старшекласснику и абитуриенту М.: Математика
( приложение к газете " Первое сентября" № 20. 2004г).
5. Олехник С.Н. и др. Нестандартные методы решения уравнений и
неравенств. - М.: Изд-во Московского университета, 1991.Кочагин В.В. ЕГЭ
2010. Математика: репетитор - М.: Эксмо, 2009.
6. Симонов А.С. Сложные проценты. Математика в школе 1998г № 5.
7. Тырымов А.А. Математика для поступающих в вузы. Часть 2.
Способы решений основных типов задач, предлагаемых на письменных
экзаменах. Системы уравнений и неравенств, задачи на составление
уравнений. - Волгоград: Учитель, 2000.
8. Хазанкин Р.Г. и др. Математическая подготовка и развитие
школьников в условиях ЕГЭ. - Уфа: НОУ "Уральский РЭК", 2004.
9. Цыпкин А.Г., Пинский А.И. Справочное пособие по методам решения
задач по математике. - М.: Наука. Главная редакция физико-математической
литературы, 1983.

34. 36