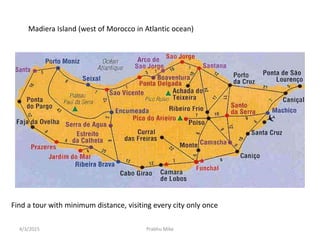
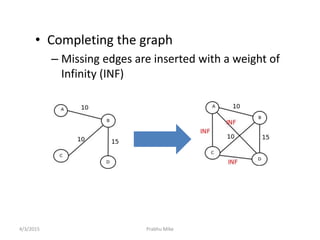
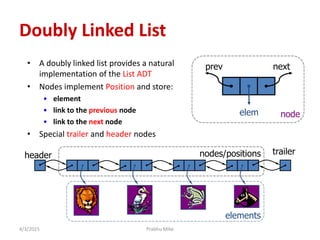
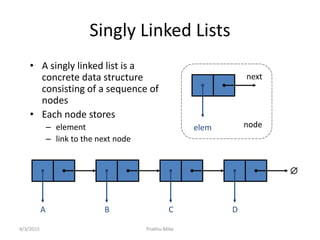
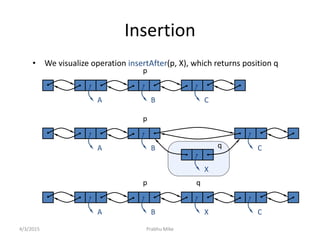
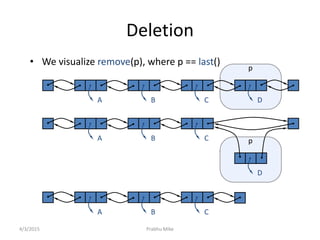
The document discusses the traveling salesman problem (TSP) and algorithms for solving it. It begins by defining the TSP as finding the shortest route to visit all cities in a set only once and return to the starting point. It then provides examples of applications that can be modeled as TSP problems, such as planning a mechanical arm route or circuit manufacturing process. The document proceeds to explain how genetic algorithms can be applied to the TSP, outlining the key steps of evolution and crossover. It concludes by discussing doubly linked lists and their advantages for implementing linked list data structures.

1. DATA STRUCTURES &
ALGORITHMS
R.PRABHU
132912
B-SEC
4/3/2015 Prabhu Mike

2. Introduction
Definition:
Given a set of cities and the distance between each
possible pair, the Travelling Salesman Problem is to
find the best possible way of ‘visiting all the cities
exactly once and returning to the starting point’
4/3/2015 Prabhu Mike

3. The Traveling Salesman
• Computer scientists call the problem of
finding an optimal path between n points the
traveling salesman problem (TSP)
• The TSP is a famous problem
– first posed by Irish mathematician
W. R. Hamilton in the 19th century
– intensely studied in
operations research and
other areas since 1930
This tour of 13,500 US cities was
generated by an advanced algorithm that
used several “tricks” to limit the number of
possible tours
http://www.tsp.gatech.edu/
Required 5 “CPU-years”
4/3/2015 Prabhu Mike

4. A genetic algorithm for a computationally demanding problem
The Traveling Salesman
• Maps and Tours
• Exhaustive Search
• Random Search
• The Genetic Algorithm
• Crossovers
4/3/2015 Prabhu Mike

5. Find a tour with minimum distance, visiting every city only once
Madiera Island (west of Morocco in Atlantic ocean)
4/3/2015 Prabhu Mike

6. Applications of TSP
• Even in its purest form the TSP, has several applications such
as planning, logistics, and the manufacture of microchips.
• Slightly modified, it appears as a sub-problem in many areas,
such as DNA sequencing.
• In these applications, the concept city represents, for example,
customers, soldering points, or DNA fragments
• The concept distance represents travelling times or cost, or a
similarity measure between DNA fragments.
• As TSP is a NP hard problem it is often used as a benchmark
for optimization techniques.
4/3/2015 Prabhu Mike

7. Applications of TSP
Mechanical arm
• When a mechanical arm is used to fasten the nuts for assembling parts, it
moves through each nut in proper order and returns to the initial position.
• The most economical travelling route will enable the mechanical arm to
finish its work within the shortest time.
Integrated circuit
• Inserting electrical elements in the manufacturing of integrated circuits
consumes certain energy when moving from one electrical element to the
other during manufacturing.
• We need to arrange the manufacturing order to minimize the energy
consumption.
In both these cases, TSP is required to be solved as a sub-problem.
4/3/2015 Prabhu Mike

8. Genetic Algorithms for TSP
Genetic algorithm has many steps in it
Evolution
• finding out good members from the population
Cross Over
• combining two parent members to form two new
different members(children) with similar characteristics
as parents.
• Some of newly formed members are altered randomly
• Keeps them from becoming identical and converging to
a local minima
4/3/2015 Prabhu Mike

9. • Completing the graph
– Missing edges are inserted with a weight of
Infinity (INF)
4/3/2015 Prabhu Mike

10. 4/3/2015
Doubly-Linked Lists
It is a way of going both directions in
a linked list, forward and reverse.
 Many applications require a quick
access to the predecessor node of some
node in list.
Prabhu Mike

11. 4/3/2015
Advantages over Singly-linked Lists
• Quick update operations:
such as: insertions, deletions at both ends (head
and tail), and also at the middle of the list.
• A node in a doubly-linked list store two
references:
• A next link; that points to the next node in the list,
and
• A prev link; that points to the previous node in the
list.
Prabhu Mike

12. 4/3/2015
Doubly Linked List
• A doubly linked list provides a natural
implementation of the List ADT
• Nodes implement Position and store:
• element
• link to the previous node
• link to the next node
• Special trailer and header nodes
prev next
elem
trailerheader nodes/positions
elements
node
Prabhu Mike

13. A linked list as
an array of records
• What are the advantages of using linked
lists?
(1) Dynamic memory allocation
(2) Efficient insertion-deletion (for sorted lists)
• Can we implement a linked list without
dynamic memory allocation ?
4/3/2015 Prabhu Mike

14. Prabhu Mike
Singly Linked Lists
• A singly linked list is a
concrete data structure
consisting of a sequence of
nodes
• Each node stores
– element
– link to the next node
next
elem node
A B C D

4/3/2015

15. Prabhu Mike
Insertion
• We visualize operation insertAfter(p, X), which returns position q
A B X C
A B C
p
A B C
p
X
q
p q
4/3/2015

16. Prabhu Mike
Insertion Algorithm
Algorithm insertAfter(p,e):
Create a new node v
v.setElement(e)
v.setPrev(p){link v to its predecessor}
v.setNext(p.getNext()) {link v to its successor}
(p.getNext()).setPrev(v) {link p’s old successor to v}
p.setNext(v) {link p to its new successor, v}
return v {the position for the element e}
4/3/2015

17. Prabhu Mike
Deletion
• We visualize remove(p), where p == last()
A B C D
p
A B C
D
p
A B C
4/3/2015

18. Prabhu Mike
Deletion Algorithm
Algorithm remove(p):
t = p.element {a temporary variable to hold the
return value}
(p.getPrev()).setNext(p.getNext()) {linking out p}
(p.getNext()).setPrev(p.getPrev())
p.setPrev(null) {invalidating the position p}
p.setNext(null)
return t
4/3/2015

19. Thank
you..
4/3/2015 Prabhu Mike