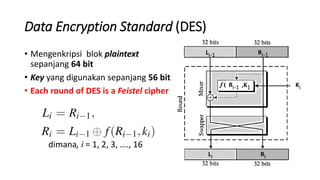
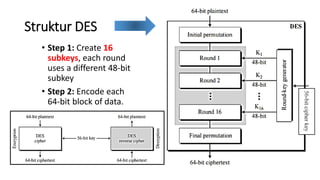
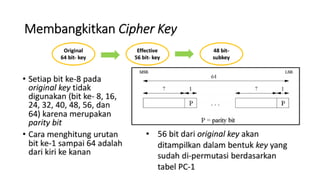
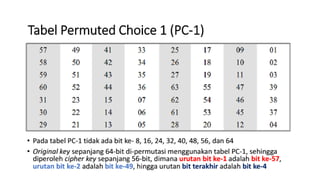
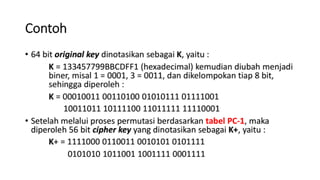
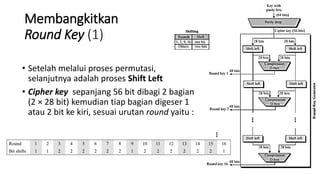
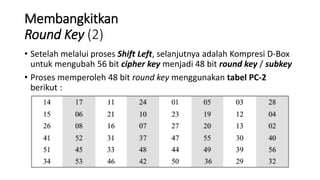
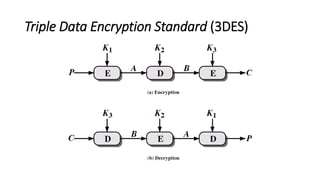
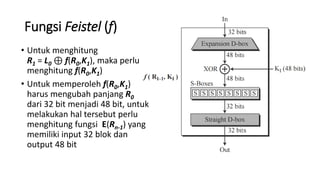
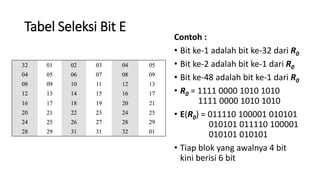
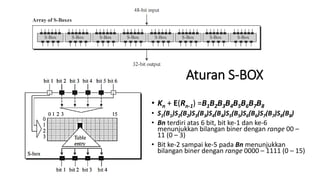
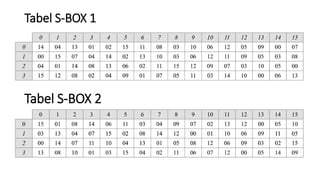
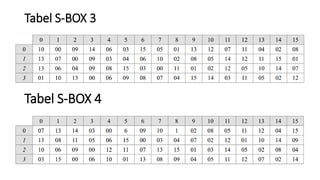
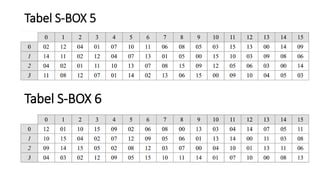
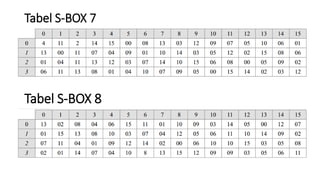
1. Data Encryption Standard (DES) adalah algoritma enkripsi blok yang mengenkripsi blok plaintext sepanjang 64 bit menggunakan key 56 bit. 2. DES bekerja berdasarkan struktur Feistel cipher dimana plaintext dibagi menjadi dua bagian dan dioperasikan secara berulang menggunakan subkey yang dihasilkan dari key utama. 3. Proses enkripsi DES terdiri atas inisial permutasi, pemisahan plaintext, operasi XOR, S-box, dan permutasi akhir

1. Data Encryption Standard (DES)

2. Data Encryption Standard (DES)
• Mengenkripsi blok plaintext
sepanjang 64 bit
• Key yang digunakan sepanjang 56 bit
• Each round of DES is a Feistel cipher
dimana, i = 1, 2, 3, …., 16
Li-1
Ri-1 ,K1
Ri-1
Li Ri
Ki

3. Struktur DES
• Step 1: Create 16
subkeys, each round
uses a different 48-bit
subkey
• Step 2: Encode each
64-bit block of data.

7. Membangkitkan
Round Key (1)
• Setelah melalui proses permutasi,
selanjutnya adalah proses Shift Left
• Cipher key sepanjang 56 bit dibagi 2 bagian
(2 × 28 bit) kemudian tiap bagian digeser 1
atau 2 bit ke kiri, sesuai urutan round yaitu :

8. Cipher key (K+) 56 bit dibagi menjadi 2 bagian yaitu Cn dan Dn, dimana 1 ≤ n ≤ 16
K+ = 1111000 0110011 0010101 0101111 0101010 1011001 1001111 0001111
C0 = 1111000011001100101010101111 D0 = 0101010101100110011110001111
C1 = 1110000110011001010101011111
D1 = 1010101011001100111100011110
C2 = 1100001100110010101010111111
D2 = 0101010110011001111000111101
C3 = 0000110011001010101011111111
D3 = 0101011001100111100011110101
C4 = 0011001100101010101111111100
D4 = 0101100110011110001111010101
C5 = 1100110010101010111111110000
D5 = 0110011001111000111101010101
C6 = 0011001010101011111111000011
D6 = 1001100111100011110101010101
C7 = 1100101010101111111100001100
D7 = 0110011110001111010101010110
C8 = 0010101010111111110000110011
D8 = 1001111000111101010101011001
C9 = 0101010101111111100001100110
D9 = 0011110001111010101010110011
C10 = 0101010111111110000110011001
D10 = 1111000111101010101011001100
C11 = 0101011111111000011001100101
D11 = 1100011110101010101100110011
C12 = 0101111111100001100110010101
D12 = 0001111010101010110011001111
C13 = 0111111110000110011001010101
D13 = 0111101010101011001100111100
C14 = 1111111000011001100101010101
D14 = 1110101010101100110011110001
C15 = 1111100001100110010101010111
D15 = 1010101010110011001111000111
C16 = 1111000011001100101010101111
D16 = 0101010101100110011110001111

9. Membangkitkan
Round Key (2)
• Setelah melalui proses Shift Left, selanjutnya adalah Kompresi D-Box
untuk mengubah 56 bit cipher key menjadi 48 bit round key / subkey
• Proses memperoleh 48 bit round key menggunakan tabel PC-2
berikut :

10. • Hasil dari proses Shift Left yaitu Cn dan Dn selanjutnya diubah
menjadi subkey Kn sepanjang 48 bit, menggunakan tabel PC-2.
C1D1 = 1110000 1100110 0101010 1011111 1010101 0110011 0011110 0011110
K1 = 000110 110000 001011 101111 111111 000111 000001 110010
K2 = 011110 011010 111011 011001 110110 111100 100111 100101
K3 = 010101 011111 110010 001010 010000 101100 111110 011001
K4 = 011100 101010 110111 010110 110110 110011 010100 011101
K5 = 011111 001110 110000 000111 111010 110101 001110 101000
K6 = 011000 111010 010100 111110 010100 000111 101100 101111
K7 = 111011 001000 010010 110111 111101 100001 100010 111100
K8 = 111101 111000 101000 111010 110000 010011 101111 111011
K9 = 111000 001101 101111 101011 111011 011110 011110 000001
K10 = 101100 011111 001101 000111 101110 100100 011001 001111
K11 = 001000 010101 111111 010011 110111 101101 001110 000110
K12 = 011101 010111 000111 110101 100101 000110 011111 101001
K13 = 100101 111100 010111 010001 111110 101011 101001 000001
K14 = 010111 110100 001110 110111 111100 101110 011100 111010
K15 = 101111 111001 000110 001101 001111 010011 111100 001010
K16 = 110010 110011 110110 001011 000011 100001 011111 110101

11. Proses Enkripsi 64 Bit Plaintext
• Permutasi awal
• Membagi plaintext menjadi 2, bagian kiri Li dan bagian kanan Ri,
dimana, i = 1, 2, 3, …., 16
• Bagian Kanan Ri-1 menjadi bagian kiri Li
• Menghitung fungsi Feistel (f) dengan input bagian kanan Ri-1 dan
subkey Kn, dimana n = 1, 2, 3, …., 16
• Operasi XOR antara bagian kiri Li-1 dan fungsi Feistel (f), kemudian
menjadi bagian kanan Ri
• Permutasi akhir

12. Initial Permutation (IP)
• Plaintext sepanjang 64 bit di-permutasi
berdasarkan tabel IP
• Pada tabel IP bit ke-1 adalah bit ke-58
dari plaintext, bit ke-2 adalah bit ke-50
dari plaintext, hingga bit terakhir adalah
bit ke-7 dari plaintext
• Bila M adalah plaintext, yaitu :
M = 0123456789ABCDEF
M = 0000 0001 0010 0011 0100 0101
0110 0111 1000 1001 1010 1011
1100 1101 1110 1111
• M di-permutasi menjadi IP
IP = 1100 1100 0000 0000 1100 1100
1111 1111 1111 0000 1010 1010
1111 0000 1010 1010

13. Membagi Plaintext Menjadi 2 Bagian
• Blok IP dibagi menjadi 2 yaitu bagian kiri L0 32 bit dan bagian
kanan R0 32 bit
• IP = 1100 1100 0000 0000 1100 1100 1111 1111 L0
1111 0000 1010 1010 1111 0000 1010 1010 R0
• L0 = 1100 1100 0000 0000 1100 1100 1111 1111
R0 = 1111 0000 1010 1010 1111 0000 1010 1010
L1 = R0 = 1111 0000 1010 1010 1111 0000 1010 1010
• Bagian kanan R0 akan diletakkan pada bagian kiri L1 tanpa perubahan
dimana, i = 1, 2, 3, …., 16

14. Fungsi Feistel (f)
• Untuk menghitung
R1 = L0 ⊕ f(R0,K1), maka perlu
menghitung f(R0,K1)
• Untuk memperoleh f(R0,K1)
harus mengubah panjang R0
dari 32 bit menjadi 48 bit, untuk
melakukan hal tersebut perlu
menghitung fungsi E(Rn-1) yang
memiliki input 32 blok dan
output 48 bit

15. Tabel Seleksi Bit E
Contoh :
• Bit ke-1 adalah bit ke-32 dari R0
• Bit ke-2 adalah bit ke-1 dari R0
• Bit ke-48 adalah bit ke-1 dari R0
• R0 = 1111 0000 1010 1010
1111 0000 1010 1010
• E(R0) = 011110 100001 010101
010101 011110 100001
010101 010101
• Tiap blok yang awalnya 4 bit
kini berisi 6 bit

16. Operasi XOR antara Rn-1 dan K1
• Untuk memperoleh nilai dari fungsi Feistel maka perlu dihitung
Kn ⊕ E(Rn-1)
• Contoh :
K1 = 000110 110000 001011 101111111111 000111 000001 110010
E(R0) = 011110 100001 010101 010101 011110 100001 010101 010101
K1 ⊕ E(R0) = 011000 010001 011110 111010 100001 100110 010100 100111
• Hasil dari operasi XOR diatas adalah 8 blok yang terdiri atas 6 bit tiap
blok , kemudian perlu diubah agar menjadi 8 blok yang terdiri atas 4
bit tiap bloknya, menggunakan tabel S-Box

17. Aturan S-BOX
• Kn + E(Rn-1) =B1B2B3B4B5B6B7B8
• S1(B1)S2(B2)S3(B3)S4(B4)S5(B5)S6(B6)S7(B7)S8(B8)
• Bn terdiri atas 6 bit, bit ke-1 dan ke-6
menunjukkan bilangan biner dengan range 00 –
11 (0 – 3)
• Bit ke-2 sampai ke-5 pada Bn menunjukkan
bilangan biner dengan range 0000 – 1111 (0 – 15)

18. Tabel S-BOX 1
Tabel S-BOX 2

19. Tabel S-BOX 3
Tabel S-BOX 4

20. Tabel S-BOX 5
Tabel S-BOX 6

21. Tabel S-BOX 7
Tabel S-BOX 8

22. Contoh
• K1 ⊕ E(R0) = 011000 010001 011110 111010 100001 100110 010100 100111
S1(B1) S2(B2) S3(B3) S4(B4) S5(B5) S6(B6) S7(B7) S8(B8)
Misalkan S1(B1) = 011000, bit ke-1 adalah 0 dan bit ke-6 adalah 0, maka
desimalnya adalah 00 =0. Sedangkan bit ke-2 hingga 5 adalah 1100,
maka desimalnya adalah 12. Maka dapat kita lihat pada tabel S-Box 1,
diperoleh nilai desimal 5, yang mana binernya adalah 0101
Sehingga,
S1(B1) S2(B2) S3(B3) S4(B4) S5(B5) S6(B6) S7(B7) S8(B8)
0101 1100 1000 0010 1011 0101 1001 0111

23. Tabel Permutasi P
• Proses terakhir untuk memperoleh nilai fungsi feistel yaitu :
f = P(S1(B1)S2(B2)...S8(B8))
• Permutasi P menggunakan tabel permutasi, dimana inputnya adalah
32 bit dan outputnya adalah 32 bit

24. Perhitungan Fungsi Feistel
f = P(S1(B1)S2(B2)...S8(B8))
S1(B1)S2(B2)S3(B3)S4(B4)S5(B5)S6(B6)S7(B7)S8(B8)
0101 1100 1000 0010 1011 0101 1001 0111
f = 0010 0011 0100 1010 1010 1001 1011 1011
= 1100 1100 0000 0000 1100 1100 1111 1111
⊕ 0010 0011 0100 1010 1010 1001 1011 1011
= 1110 1111 0100 1010 0110 0101 0100 0100
R1 = L0 ⊕ f(R0,K1),

25. Proses Selanjutnya
• Pada putaran ke-2 adalah L2 = R1 dan R2 =L1 ⊕ f(R1, K2)
• Demikian seterusnya hingga putaran ke-16
• Pada putaran ke-16 yaitu blok L16 dan R16 akan ditukar posisinya
sehingga menjadi R16L16
• Kemudian dilakukan permutasi akhir berdasarkan tabel permutasi IP-1

26. Tabel Permutasi IP-1
L16 = 0100 0011 0100 0010
0011 0010 0011 0100
R16 = 0000 1010 0100 1100
1101 1001 1001 0101
R16L16 = 00001010 01001100
11011001 10010101
01000011 01000010
00110010 00110100
IP-1 = 10000101 11101000 00010011
01010100 00001111 00001010
10110100 00000101
IP-1 = 85E813540F0AB405.

27. Hasil Proses Enkripsi
• Plaintext M = 0123456789ABCDEF
• Original key K = 133457799BBCDFF1
• Ciphertext C = 85E813540F0AB405
• Untuk proses dekripsi adalah kebalikan dari proses enkripsi,
langkahnya sama seperti enkripsi, tetapi urutan subkey yang
digunakan terbalik
• Bila enkripsi subkey 1 untuk round 1 hingga subkey 16 untuk round 16
• Bila dekripsi subkey 16 untuk round 1 hingga subkey 1 untuk round 16

28. Triple Data Encryption Standard (3DES)