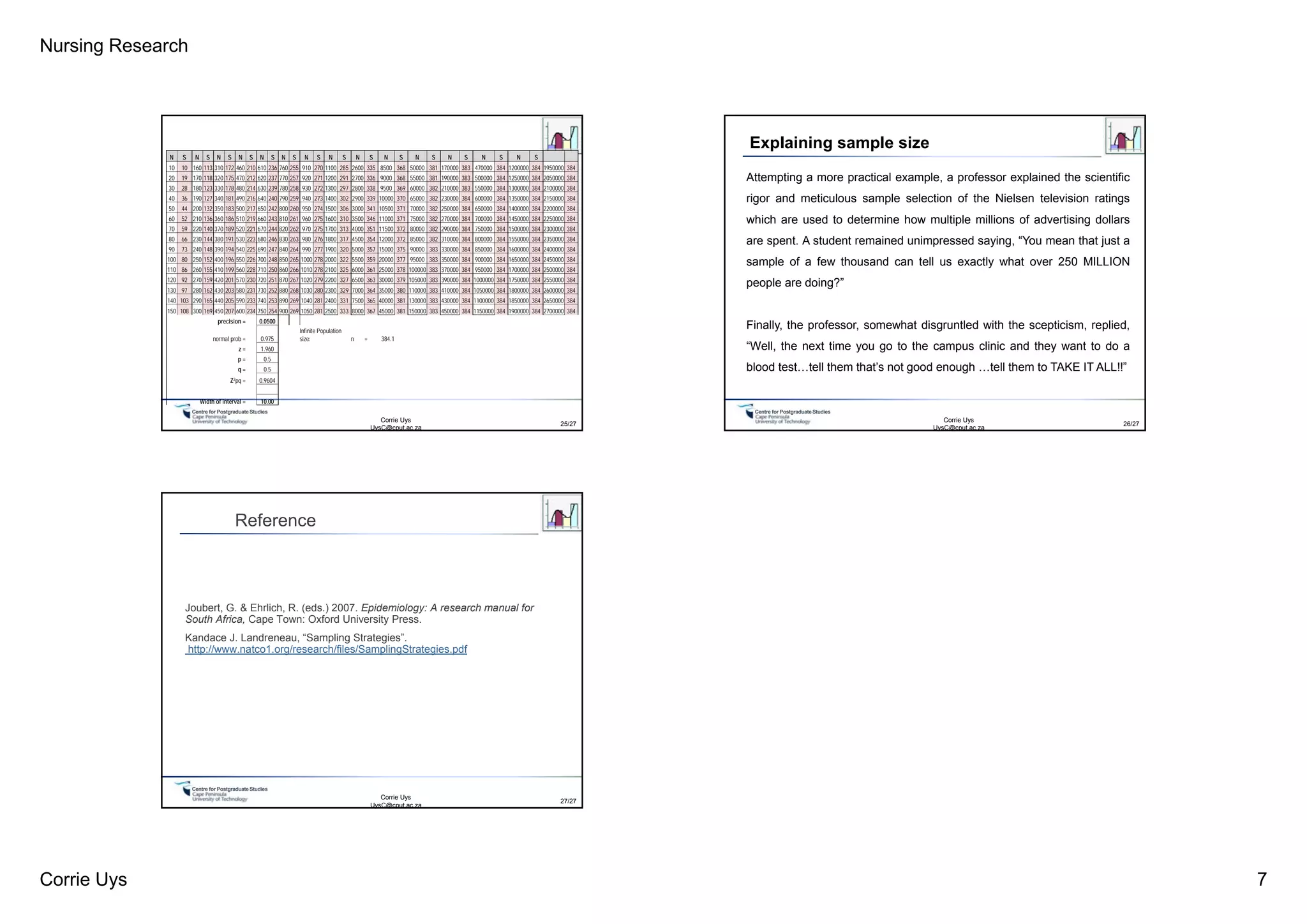
This document discusses various methods for collecting data and sampling strategies in nursing research. It begins by defining key terms like census, sample survey, experiment, and observational study as different data collection methods. It then covers advantages and disadvantages of these methods. The document primarily focuses on explaining different sampling strategies, including probability and non-probability techniques. It discusses considerations for calculating appropriate sample sizes and provides an example of a sample size calculation. Overall, the document provides an overview of collecting evidence and sampling in nursing research.