1. Introduction to Algorithms 1.1 What is an Algorithm? An algorithm is a finite set of instructions that, if followed, accomplishes a particular task. It is a well-defined procedure that takes some input, performs a sequence of computational steps, and produces an output. 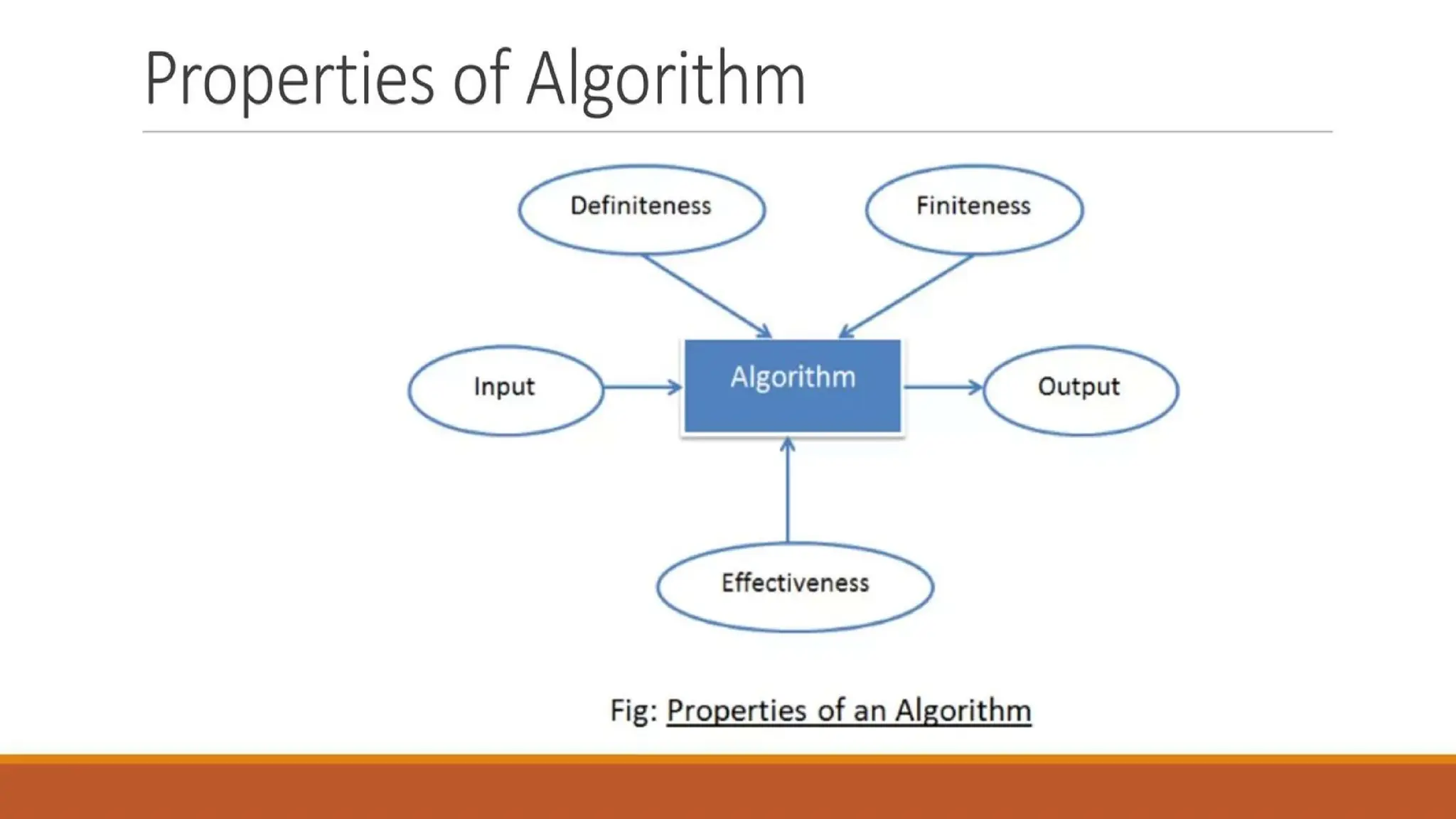Formally: “An algorithm is a step-by-step procedure for solving a problem in a finite amount of time.” 1.2 Characteristics of an Algorithm For a procedure to qualify as an algorithm, it must satisfy the following properties: Finiteness – The algorithm must terminate after a finite number of steps. Definiteness – Each step of the algorithm must be clear and unambiguous. Input – An algorithm should have zero or more inputs. Output – An algorithm should produce at least one output. Effectiveness – Every step of the algorithm must be basic enough to be carried out by a computer in a finite amount of time. 2. Importance of Algorithm Analysis Writing an algorithm is not enough; we also need to evaluate its efficiency. With large datasets, the efficiency of an algorithm plays a crucial role in execution speed and resource usage. 2.1 Why Analyze Algorithms? To choose the best algorithm for solving a problem. To compare algorithms based on time and space requirements. To understand the scalability of the algorithm as input size grows. 3. Algorithm Design Goals When designing an algorithm, the following goals are kept in mind: Correctness – Algorithm should solve the problem accurately. Efficiency – It should use minimum resources (time and memory). Readability & Simplicity – Easy to understand, maintain, and implement. Scalability – Should handle larger inputs without breaking down. Generality – Should be applicable to different types of inputs. 4. Algorithm Analysis 4.1 Types of Analysis Worst Case Analysis Maximum time taken on any input of size n. Guarantees performance in the worst scenario. Example: In Linear Search, worst case is when the element is not present. Best Case Analysis Minimum time taken on any input of size n. Example: In Linear Search, best case is when the first element matches. Average Case Analysis Expected time over all possible inputs. Often provides a realistic measure. 4.2 Asymptotic Notations Asymptotic analysis describes the running time of an algorithm in terms of input size n for large inputs. Big-O Notation (O) Represents the upper bound of the growth rate. Example: Linear Search → O(n). 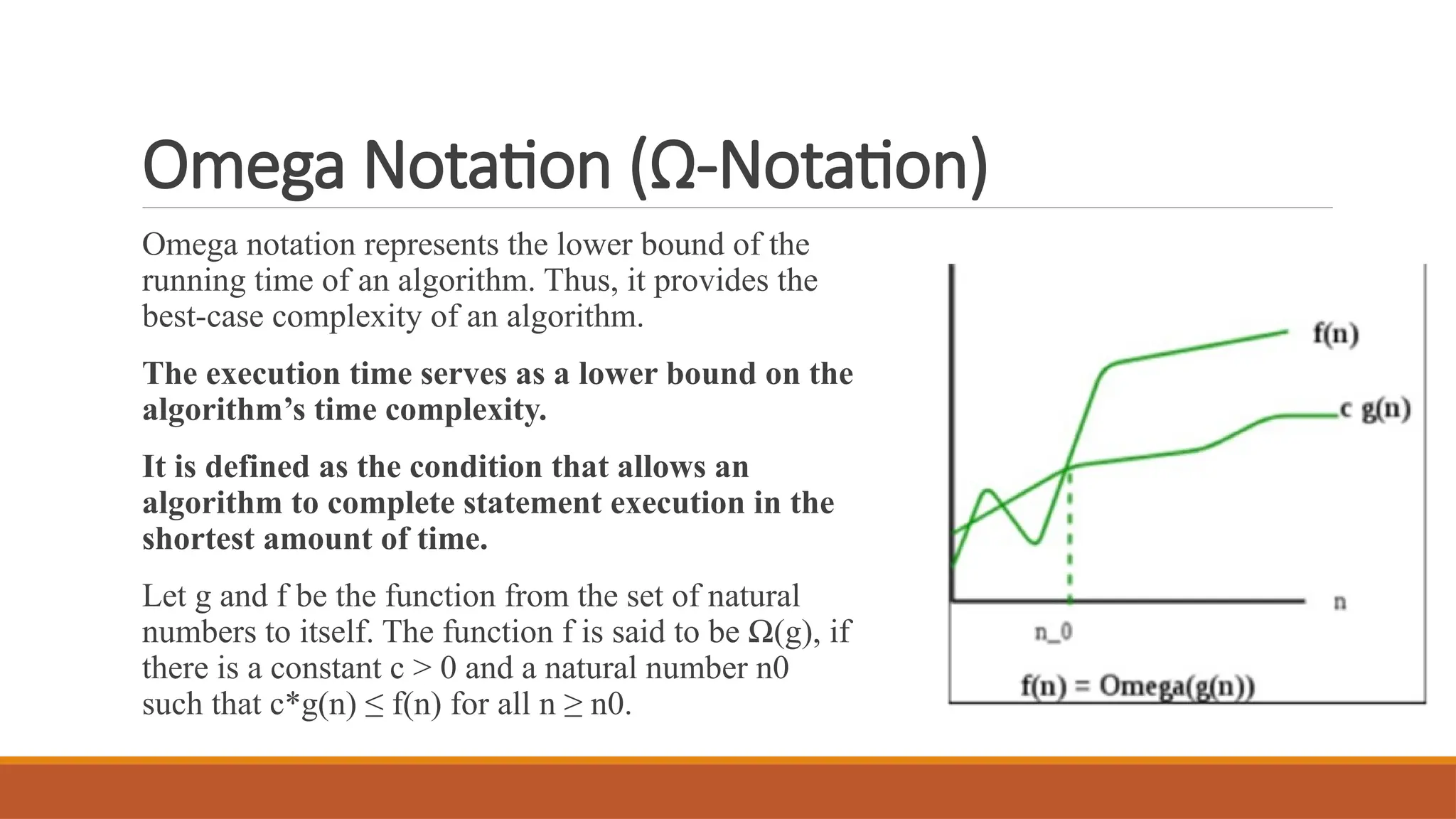Omega Notation (Ω) Represents the lower bound of the growth rate. Example: Linear Search → Ω(1). Theta Notation (Θ) Represents the tight bound (both upper and lower). Example: Linear Search → Θ(n). 5. Growth of Functions The efficiency of an algorithm is influenced by how its running time grows with input size. Some common growth rates: Constant → O(1) Logarithmic → O(log n) Linear → O(n) Linearithmic → O(n log n) Quadratic → O(n²) Cubic → O(n³) Exponential → O(2^n) Factorial → O(n!) 6. Recurrence Relations Many rec

1. DESIGN AND ANALYSIS OF
ALGORITHM (BCS503) -
INTROUCTION
MR. ABHAY CHAUDHARY
DEPARTMENT OF COMPUTER SCIENCE AND ENGINEERING
NITRA TECHNICAL CAMPUS

21. Growth of Functions
Growth of Functions describes how the time or space requirements of an
algorithm
grow with the size of the input. The growth rate helps in understanding the
efficiency of
an algorithm.
Examples:
• Polynomial Growth: O(n2) - Example: Bubble Sort algorithm.
• Exponential Growth: O(2n) - Example: Recursive Fibonacci algorithm.

22. Asymptotic Notations
Asymptotic Notations are type of notation that allow you to analyze an algorithm’s running
time by identifying its behaviour as its input size grows. This is also referred to as an
algorithm’s growth rate.
We can compare space and time complexity using asymptotic analysis. It compares two
algorithms based on changes in their performance as the input size is increased or decreased.
There are mainly three asymptotic notations we use for the analysis of algorithms.
They are:
1. Big-O Notation (O-notation)
2. Omega Notation (Ω-notation)
3. Theta Notation (Θ-notation)

23. Big-O Notation (O-notation)
Big-O notation represents the upper bound of the running time of an
algorithm. Therefore, it gives the worst-case complexity of an algorithm.
•It is the most widely used notation for Asymptotic analysis.
•It specifies the upper bound of a function.
•The maximum time required by an algorithm or the worst-case time
complexity.
•It returns the highest possible output value(big-O) for a given input.
•Big-Oh (Worst Case): It is defined as the condition that allows an algorithm
to complete statement execution in the longest amount of time possible.
If f(n) describes the running time of an algorithm, f(n) is O(g(n)) if there
exist a positive constant C and n_0 such that, 0 ≤ f(n) ≤ cg(n) for all n ≥ n_0.

24. Omega Notation (Ω-Notation)
Omega notation represents the lower bound of the
running time of an algorithm. Thus, it provides the
best-case complexity of an algorithm.
The execution time serves as a lower bound on the
algorithm’s time complexity.
It is defined as the condition that allows an
algorithm to complete statement execution in the
shortest amount of time.
Let g and f be the function from the set of natural
numbers to itself. The function f is said to be Ω(g), if
there is a constant c > 0 and a natural number n0
such that c*g(n) ≤ f(n) for all n ≥ n0.

25. Theta Notation (Θ-Notation)
Theta notation encloses the function from above and
below. Since it represents the upper and the lower
bound of the running time of an algorithm, it is used for
analyzing the averagecase complexity of an algorithm.
Theta (Average Case) you add the running times for
each possible input combination and take the average in
the average case.
Let g and f be the function from the set of natural
numbers to itself. The function f is said to be Θ(g), if
there are constants c1, c2 > 0 and a natural number n0
such that c1* g(n) ≤ f(n) ≤ c2 * g(n) for all n ≥ n0