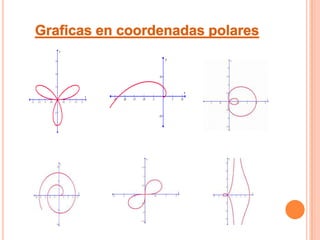
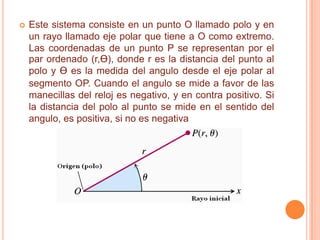
Un sistema de coordenadas define la posición de puntos en un espacio geométrico a través de valores como distancia y ángulo desde un origen. Las coordenadas polares usan un ángulo y distancia para definir puntos en un plano. Aunque las cartesianas son comunes, las polares permiten expresar curvas de forma más simple. Las coordenadas polares de un punto P son el par ordenado (r,θ), donde r es la distancia al polo y θ es el ángulo desde el eje polar. El área de una región polar se calcula integrando la función r

2.  Un sistema de coordenadas es un conjunto de valores
que permiten definir univocamente la posicion de
cualquier punto de un espacio geometrico respecto de
un punto denominado origen. El conjunto de ejes,
puntos o planos que confluyen en el origen y a partir de
los cuales se calculan las coordenadas de cualquier
punto, constituyen lo que se denomina sistema de
referencia.

3.  Las coordenadas polares son un sistema que define la
posicion de un punto en un espacio bidimensional
consistente en un angulo y una distancia.
 En muchos casos es util utilizar las coordenadas
cartesianas para definir una funcion en el plano o en el
espacio. En ocasiones es conveniente usar otros
sistemas de las mismas. Por ejemplo, en el plano
podemos usar las coordenadas polares, que permiten
expresar ciertas curvas en forma mucho mas simple que
las ecuaciones que ligan sus coordenadas cartesianas.
En el espacio, en lugar de usar las cartesianas, podemos
usar las coordenadas cilíndricas o esféricas.

4.  Este sistema consiste en un punto O llamado polo y en
un rayo llamado eje polar que tiene a O como extremo.
Las coordenadas de un punto P se representan por el
par ordenado (r,Ɵ), donde r es la distancia del punto al
polo y Ɵ es la medida del angulo desde el eje polar al
segmento OP. Cuando el angulo se mide a favor de las
manecillas del reloj es negativo, y en contra positivo. Si
la distancia del polo al punto se mide en el sentido del
angulo, es positiva, si no es negativa

5.  La grafica de una ecuación polar r = f(Ɵ) es el conjunto de
puntos (x,y) para los cuales x = r cos Ɵ , y = r sen Ɵ y r = f (Ɵ).
En otros terminos, la grafica de una ecuacion polar es una
grafica en el plano xy de todos los puntos cuyas coordenadas
polares satisfacen la ecuacion dada.
 La clave para dibujar las mismas de una ecuacion polar, es
mantener siempre presente que representan las coordenadas
polares.
 Con estos conceptos basicos de localizacion de puntos en el
sistema de coordenadas polares, podemos graficar funciones y
no solo puntos. En este tipo de funciones la variable
independiente es Ɵ y la dependiente es r, asi que las funciones
son del tipo r = r(Ɵ). El metodo para graficar estas funciones es
el siguiente, primero graficamos la funcion r = r(Ɵ) en
coordenadas rectangulares y a partir de esa grafica trazamos la
correspondiente en polares. Guiandonos con la dependencia
de r con respecto a Ɵ.

7.  En la figura se observa que la superficie de un sector
circular de radio r viene dada por:
 la funcion dada por r= f(q), donde f es continua y no
negativa en el intervalo [ a , b ] . La region limitada por
la grafica para hallar el area de esta region, partimos el
intervalo [ a , b ] en n subintervalos iguales a=q<q
< q <........< q < q = b

8.  A continuacion aproximamos el area de la region por la
suma de las mismas de los n sectores,
 Luego de haber notado el teorema anterior, podemos
decir que usar la formula para hallar el area de una
region limitada por la grafica de una funcion continua no
negativa. Sin embargo, no es necesariamente valida si f
toma valores positivos y negativos en el intervalo [ a , b
].
 Algunas veces lo mas dificil a la hora de hallar el
area de una region polar es determinar los limites de
integracion. Un buen dibujo de la region puede ayudar
mucho en estos casos.