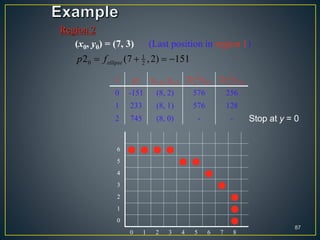
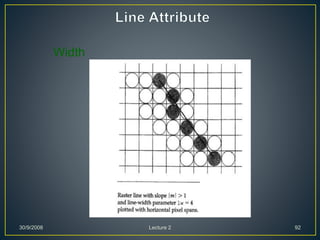
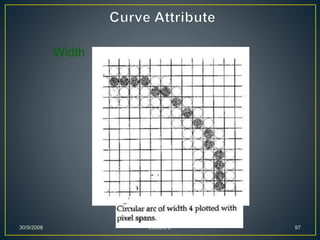
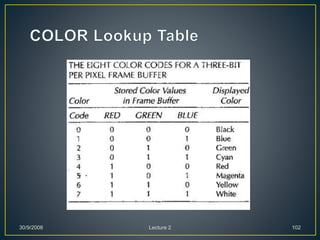
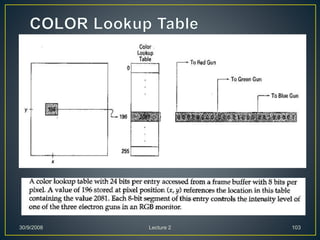
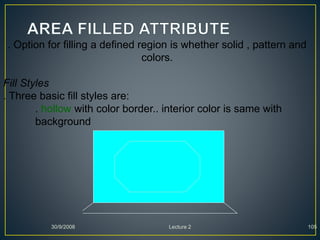
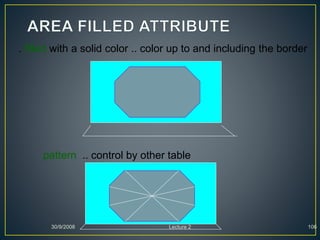
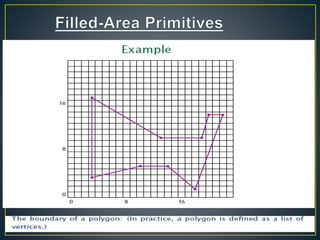
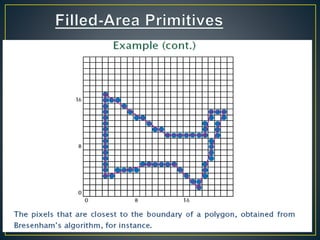
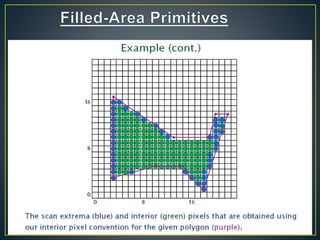
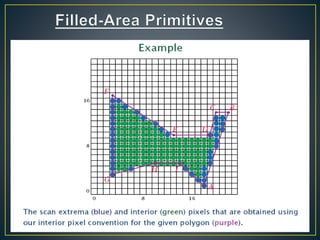
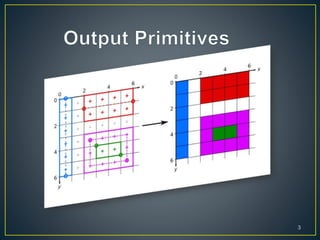
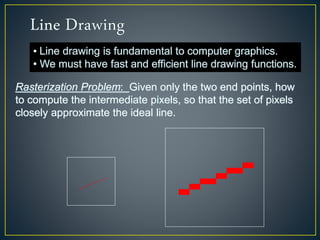
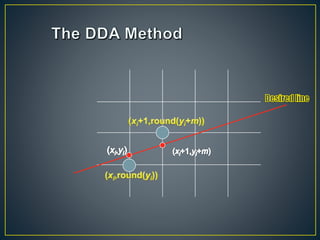
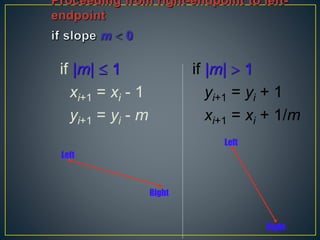
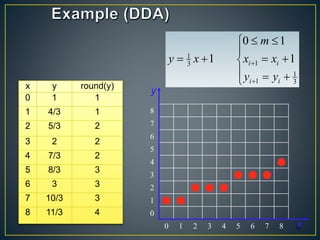
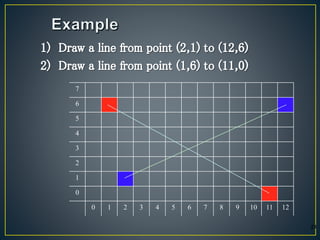
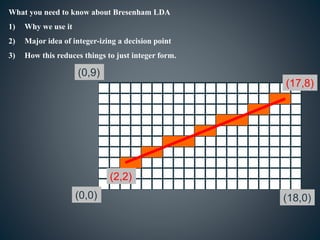
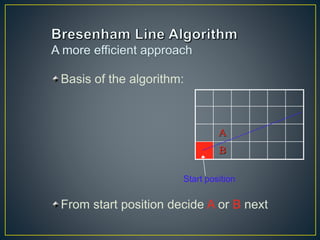
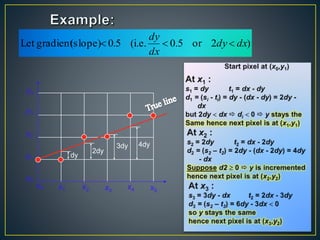
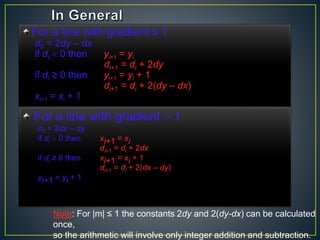
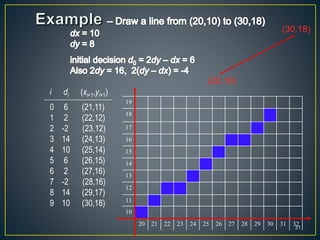
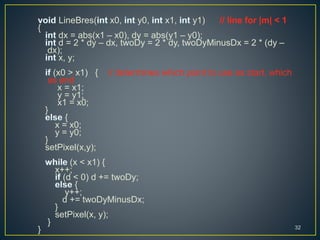
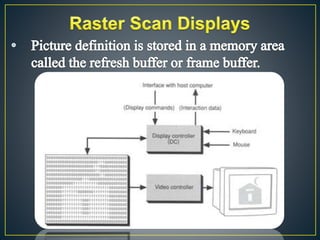
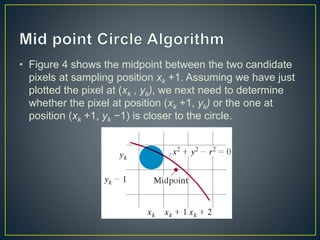
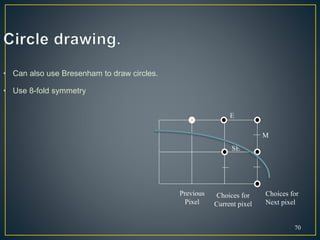
The document describes various computer graphics output primitives and algorithms for drawing them, including lines, circles, and filled areas. It discusses line drawing algorithms like DDA, Bresenham's, and midpoint circle algorithms. These algorithms use incremental integer calculations to efficiently rasterize primitives by determining the next pixel coordinates without performing floating point calculations at each step. The midpoint circle algorithm in particular uses a "circle function" and incremental updates to its value to determine whether the next pixel is inside or outside the circle boundary.

1. 1
 Unit - 1
Father of Computer Graphics
Ivan Sutherland

2. Output Primitives
Line Drawing Algorithms
DDA Algorithm
Midpoint Algorithm
Bersenhem’s Algorithm
Circle Drawing Algorithms
Midpoint Circle Algorithm
Antialiasing
Fill-Area Algorithms
2

3. 3

4. Describes the geometry of objects and –
typically referred to as geometric
primitives.
Examples: point, line, text, filled region,
images, quadric surfaces, spline curves
Each of the output primitives has its own
set of attributes.
The basic objects out of which a graphics
display is created are called Output
Primitives

5. • Points
• Attributes: Size, Color.
glPointSize(p);
glBegin(GL_POINTS);
glVertex2d(x1, y1);
glVertex2d(x2, y2);
glVertex2d(x3, y3);
glEnd()

6. • Lines
• Attributes: Color, Thickness, Type
glLineWidth(p);
glBegin(GL_LINES);
glVertex2d(x1, y1);
glVertex2d(x2, y2);
glVertex2d(x3, y3);
glVertex2d(x4, y4);
glEnd()

7. Output Primitive Attributes
Point Size
Color
Line Thickness (1pt, 2pt …)
Type (Dashed, Dotted, Solid)
Color
7

8. 8

9. Rasterization Problem: Given only the two end points, how
to compute the intermediate pixels, so that the set of pixels
closely approximate the ideal line.

10. • The digital differential analyser
(DDA) algorithm takes an
incremental approach in order to
speed up scan conversion
• Simply calculate yk+1 based on
yk
The original differential
analyser was a physical
machine developed by
Vannevar Bush at MIT in the
1930’s in order to solve
ordinary differential equations.

11. m
x
y



x y
0 1
1 4
2 7
3 10
4 13
5 16
my
x 1



i.e. y = 3x + 1 m = 3
Do not use
y = 3x + 1
to calculate y.
Use m

12. Uses differential equation of the line : m
If slope then increment x in steps of 1
pixel and find corresponding y-values.
If slope then increment y in steps of 1
pixel and find corresponding x-values.








 
 
 
 
step through in x step through in y

17. if |m|  1
xi+1 = xi - 1
yi+1 = yi - m
if |m|  1
yi+1 = yi + 1
xi+1 = xi + 1/m
Left
Right
Left
Right

18. 










3
1
1
13
1
1
10
1
ii
ii
yy
xx
m
xy
x y round(y)
0 1 1
1 4/3 1
2 5/3 2
3 2 2
4 7/3 2
5 8/3 3
6 3 3
7 10/3 3
8 11/3 4
18
8
7
6
5
4 
3   
2   
1  
0
0 1 2 3 4 5 6 7 8
y
x

19. 









)(
1
1
83
3
1
1
1
ii
ii
xx
yy
m
xy
y x round(x
)
8 0 0
7 1/3 0
6 2/3 1
5 1 1
4 4/3 1
3 5/3 2
2 2 2
1 7/3 2
0 8/3 3
19
8 
7 
6 
5 
4 
3 
2 
1 
0 
0 1 2 3 4 5 6 7 8
y
x

20. 20

21. 7
6
5
4
3
2
1
0
0 1 2 3 4 5 6 7 8 9 10 11 12
21

22. p
p
p
n
nx
x
1

22

23. yp = mxp
yk = y0 + round(kyp)
pk = (kxp)(2y) – round(kyp)(2x) + 2y – x
4
4
18
4
1415


 px
23

24. Jack Bresenham worked for
27 years at IBM before
entering academia.
Bresenham developed his
famous algorithms at IBM
in the early 1960s

25. What you need to know about Bresenham LDA
1) Why we use it
2) Major idea of integer-izing a decision point
3) How this reduces things to just integer form.
(17,8)
(2,2)
(0,0) (18,0)
(0,9)

26. Basis of the algorithm:
From start position decide A or B next
A
B
Start position

27. o For a given value of x
o One pixel lies at distance above the line, and
o One pixel lies at distance below the line
True line

28. If di  0, then closest pixel is below true line (si
smaller)
If di  0, then closest pixel is above true line (ti
smaller)
We must calculate the new values for as we move
along the line.

29. )2or5.0(i.e.0.5(slope)gradientLet dxdy
dx
dy

29
3dy
2dy
dy
4dy
x1 x2 x3
x4 x5
x0
y0
y1
y2
y3
y5

30. For a line with gradient ≤ 1
d0 = 2dy – dx
if di  0 then yi+1 = yi
di+1 = di + 2dy
if di ≥ 0 then yi+1 = yi + 1
di+1 = di + 2(dy – dx)
xi+1 = xi + 1
For a line with gradient  1
d0 = 2dx – dy
if di  0 then xi+1 = xi
di+1 = di + 2dx
if di ≥ 0 then xi+1 = xi + 1
di+1 = di + 2(dx – dy)
yi+1 = yi + 1
Note: For |m| ≤ 1 the constants 2dy and 2(dy-dx) can be calculated
once,
so the arithmetic will involve only integer addition and subtraction.

31. 19
18
17
16
15
14
13
12
11
10
20 21 22 23 24 25 26 27 28 29 30 31 32
31
(20,10)
(30,18)
i di (xi+1,yi+1)
0 6 (21,11)
1 2 (22,12)
2 -2 (23,12)
3 14 (24,13)
4 10 (25,14)
5 6 (26,15)
6 2 (27,16)
7 -2 (28,16)
8 14 (29,17)
9 10 (30,18)

32. LineBres( x0, y0, x1, y1) // line for |m| < 1
{
dx = abs(x1 – x0), dy = abs(y1 – y0);
d = 2 * dy – dx, twoDy = 2 * dy, twoDyMinusDx = 2 * (dy –
dx);
x, y;
(x0 > x1) { // determines which point to use as start, which
as end
x = x1;
y = y1;
x1 = x0;
}
{
x = x0;
y = y0;
}
setPixel(x,y);
(x < x1) {
x++;
(d < 0) d += twoDy;
{
y++;
d += twoDyMinusDx;
}
setPixel(x, y);
}
} 32

33. • Special cases can be handled separately
• Horizontal lines (y = 0)
• Vertical lines (x = 0)
• Diagonal lines (|x| = |y|)
• directly into the frame-buffer without processing
them through the line-plotting algorithms.
33

35. • Raster:
• Pixel:
• Scan Line:

39. • Refresh buffer frame buffer:
intensity

40. “painted”
scan line

41. • Intensity range for pixel positions
depends on the capability of the
raster system.
• A black-and-white system: each
screen point is either on or off, so
only one bit per pixel is needed to
control the intensity of screen
positions.

42. • On a black-and-white system
with one bit per pixel, the frame
buffer is called bitmap.
• For system with multiple bits per
pixel, the frame buffer is called
pixmap.

43. • Sometimes, refresh rates
are described in unit of
cycles per second, or Hertz
(HZ)

44. • Refreshing on raster scan
displays is carried out at
the rate 60 to 80 frame per
second.

45. • Horizontal retrace: The return
to the left of the screen, after
refreshing each scan line.

46. Vertical retrace: At the end of each frame
(displayed in 1/80th to 1/60th of a second)
the electron beam returns to the top left
corner of the screen to begin the next
frame.

47. A final stage in the implementation
procedures for line segments and other
objects is to set the frame-buffer color
values.
scan-conversion algorithms generate pixel
positions at successive unit intervals,
incremental operations can also be used to
access the frame buffer efficiently at each
step of the scan-conversion process.

48. •suppose the frame buffer array is addressed in row major
order and that pixel positions are labeled from (0, 0) at the
lower-left screen corner to (x max , y max ) at the top-right
corner.
• For a bilevel system (one bit per pixel), the frame-buffer bit
address for pixel position ( x , y ) is calculated as

49. Moving across a scan line, we can calculate the frame-buffer address for the
pixel at ( x + 1, y ) as the following offset from the address for position ( x , y ):
Stepping diagonally up to the next scan line from ( x , y ),we get to the frame-buffer
address of ( x + 1, y + 1) with the calculation
where the constant x max + 2 is precomputed once for all line segments.
Each of the address calculations involves only a single integer addition.

50. Methods for implementing these procedures depend on the capabilities of a
particular system and the design requirements of the software package.
With systems that can display a range of intensity values for each pixel, frame-
buffer address calculations include pixel width (number of bits), as well as the
pixel screen location.

51. • Line
• Defined by two endpoint coordinates
(one line segment)
glBegin(GL_LINES );
glVertex2i( 180, 15 );
glVertex2i( 10, 145 );
glEnd();
• If several vertices, a line is drawn between the first and
second, then a separate one between the third and the fourth,
etc. (isolated vertices are not drawn).

52. • Polyline
• Defined by line connecting all the points
glBegin(GL_LINE_STRIP );
glVertex2i( 180, 15 );
glVertex2i( 10, 145 );
glVertex2i( 100, 20 );
glVertex2i( 30, 150 );
glEnd();
• Draws a line between vertex 1 and vertex 2
then between vertex 2 and vertex 3
then between vertex 3 and vertex 4.

53. • Polyline
• In addition to GL_LINE_STRIP, adds a line between the last
vertex and the first one
glBegin(GL_LINE_LOOP );
glVertex2i( 180, 15 );
glVertex2i( 10, 145 );
glVertex2i( 100, 20 );
glVertex2i( 30, 150 );
glEnd();
• Draws a line between vertex 1 and vertex 2
then between vertex 2 and vertex 3
then between vertex 3 and vertex 4
then between vertex 4 and vertex 1.

54. • A circle is defined as the set of points that are all at a given
distance r from a center point (xc, yc).
• For any circle point (x, y), this distance is expressed by the
Equation
(x − xc)2 + (y − yc)2 = r 2
• We calculate the points by stepping along the x-axis in unit
steps from xc-r to xc+r and calculate y values as

55. • There are some problems with this approach:
1. Considerable computation at each step.
2. Non-uniform spacing between plotted pixels as in this
Figure.

56. • Problem 2 can be removed using the polar form:
x = xc + r cos θ
y = yc + r sin θ
• using a fixed angular step size, a circle is plotted with
equally spaced points along the circumference.

57. • Problem 1 can be overcome by considering the
symmetry of circles as in Figure 3.
• But it still requires a good deal of computation time.
• Efficient Solutions
• Midpoint Circle Algorithm

58. • To apply the midpoint method, we define a circle function:
• Any point (x,y) on the boundary of the circle with radius r
satisfies the equation fcircle(x, y)= 0.

59. • If the points is in the interior of the circle, the circle
function is negative.
• If the point is outside the circle, the circle function is
positive.
• To summarize, the relative position of any point (x,y) can
be determined by checking the sign of the circle function:

60. • The circle function tests in (3) are performed for the mid
positions between pixels near the circle path at each
sampling step. Thus, the circle function is the decision
parameter in the midpoint algorithm, and we can set up
incremental calculations for this function as we did in the
line algorithm.

61. • Figure 4 shows the midpoint between the two candidate
pixels at sampling position xk +1. Assuming we have just
plotted the pixel at (xk , yk), we next need to determine
whether the pixel at position (xk +1, yk) or the one at
position (xk +1, yk −1) is closer to the circle.

62. • Our decision parameter is the circle function (2)
evaluated at the midpoint between these two pixels:

63. • If pk < 0, this midpoint is inside the circle and the pixel on
scan line yk is closer to the circle boundary.
• Otherwise, the midpoint is outside or on the circle
boundary, and we select the pixel on scan line yk −1.
• Successive decision parameters are obtained using
incremental calculations.

64. • We obtain a recursive expression for the next decision parameter by
evaluating the circle function at sampling position xk+1 +1 = xk + 2
• where yk+1 is either yk or yk-1,depending on the sign of pk.

65. • Increments for obtaining pk+1 are either
• 2xk+1 +1 (if pk is negative) or
• 2xk+1 +1− 2yk+1 (if pk is positive)
• Evaluation of the terms 2xk+1 and 2yk+1 can also be
done incrementally as:

66. • At the start position (0, r), these two terms (2x, 2y) have
the values 0 and 2r, respectively.
• Each successive value is obtained by adding 2 to the
previous value of 2x and subtracting 2 from the previous
value of 2y.

67. • The initial decision parameter is obtained by evaluating
the circle function at the start position (x0 , y0)=(0, r):

68. • If the radius r is specified as an integer, we can simply
round p0 to
• since all increments are integers.

69. • As in Bresenham’s line algorithm, the midpoint method
calculates pixel positions along the circumference of a
circle using integer additions and subtractions, assuming
that the circle parameters are specified in screen
coordinates. We can summarize the steps in the midpoint
circle algorithm as follows.

70. 70
• Can also use Bresenham to draw circles.
• Use 8-fold symmetry
Choices for
Next pixel
M
E
SE
Previous
Pixel
Choices for
Current pixel

71. 71
• Implicit form for a circle is:
)32(chosenisEIf
)522(chosenisSEIf


poldnew
ppoldnew
xdd
yxdd
• Functions are linear equations in terms of (xp,yp)
–Termed point of evaluation
222
)()(),( ryyxxyxf cc 

72. 72
• Explicit form of line
• Inefficient, difficult to control.
• Parametric form of line.
• Express line in terms of parameter t
• DDA algorithm
• Implicit form of line
• Only need to test for ‘side’ of line.
• Bresenham algorithm.
• Can also draw circles.

73. • Ellipse – A modified circle whose radius varies from a
maximum value in one direction (major axis) to a
minimum value in the perpendicular direction (minor
axis).
73
P=(x,y)F1
F2
d1
d2
 The sum of the two distances d1 and d2, between the
fixed positions F1 and F2 (called the foci of the ellipse)
to any point P on the ellipse, is the same value, i.e.
d1 + d2 = constant

74. • Expressing distances d1 and d2 in terms of the focal
coordinates F1 = (x1, x2) and F2 = (x2, y2), we have:
• Cartesian coordinates:
• Polar coordinates:
2 2 2 2
1 1 2 2( ) ( ) ( ) ( ) constantx x y y x x y y       
22
1c c
x y
x x y y
r r
   
     
   
74
ry
rx
cos
sin
c x
c y
x x r
y y r


 
 

75. • Symmetry between quadrants
• Not symmetric between the two octants of a
quadrant
• Thus, we must calculate pixel positions along the
elliptical arc through one quadrant and then we
obtain positions in the remaining 3 quadrants by
symmetry
75
(x, y)(-x, y)
(x, -y)(-x, -y)
rx
ry

76. • Decision parameter:
2 2 2 2 2 2
( , )ellipse y x x yf x y r x r y r r  
0 if ( , ) is inside the ellipse
( , ) 0 if ( , ) is on the ellipse
0 if ( , ) is outside the ellipse
ellipse
x y
f x y x y
x y


 

76
1
Slope = -1
rx
ry 2 2
2
2
2
y
x
r xdy
Slope
dx r y
  

77. • Starting at (0, ry) we take unit steps in the x direction
until we reach the boundary between region 1 and
region 2. Then we take unit steps in the y direction
over the remainder of the curve in the first quadrant.
• At the boundary
• therefore, we move out of region 1 whenever
77
1
Slope = -1
rx
ry 2
2 2
1 2 2y x
dy
r x r y
dx
   
2 2
2 2y xr x r y

78. yi 
yi-1
xi xi+1 xi+2
78
Midpoint
Assuming that we have just plotted the pixels at (xi , yi).
The next position is determined by:
1
2
2 2 2 2 2 21
2
1 ( 1, )
( 1) ( )
i ellipse i i
y i x i x y
p f x y
r x r y r r
  
    
If p1i < 0 the midpoint is inside the ellipse  yi is closer
If p1i ≥ 0 the midpoint is outside the ellipse  yi – 1 is

79. At the next position [xi+1 + 1 = xi + 2]
OR
where yi+1 = yi
or yi+1 = yi – 1
79
1
1 1 1 2
2 2 2 2 2 21
1 2
1 ( 1, )
( 2) ( )
i ellipse i i
y i x i x y
p f x y
r x r y r r
  

  
    
2 2 2 2 2 21 1
1 1 2 21 1 2 ( 1) ( ) ( )i i y i y x i ip p r x r r y y 
         

80. Decision parameters are incremented by:
Use only addition and subtraction by obtaining
At initial position (0, ry)
80
2 2
1
2 2 2
1 1
2 if 1 0
2 2 if 1 0
y i y i
y i y x i i
r x r p
increment
r x r r y p

 
  
 
  
2 2
2 and 2y xr x r y
2
2 2
2 2 2 2 21 1
0 2 2
2 2 21
4
2 0
2 2
1 (1, ) ( )
y
x x y
ellipse y y x y x y
y x y x
r x
r y r r
p f r r r r r r
r r r r


     
  

81. Over region 2, step in the negative y direction and midpoint
is taken between horizontal pixels at each step.
81
yi 
yi-1
xi xi+1 xi+2
Midpoint
Decision parameter:
1
2
2 2 2 2 2 21
2
2 ( , 1)
( ) ( 1)
i ellipse i i
y i x i x y
p f x y
r x r y r r
  
    
If p2i > 0 the midpoint is outside the ellipse  xi is closer
If p2i ≤ 0 the midpoint is inside the ellipse  xi + 1 is

82. At the next position [yi+1 – 1 = yi – 2]
OR
where xi+1 = xi
or xi+1 = xi + 1
82
1
1 1 12
2 2 2 2 2 21
1 2
2 ( , 1)
( ) ( 2)
i ellipse i i
y i x i x y
p f x y
r x r y r r
  

  
    
2 2 2 2 21 1
1 1 2 22 2 2 ( 1) ( ) ( )i i x i x y i ip p r y r r x x 
         

83. Decision parameters are incremented by:
At initial position (x0, y0) is taken at the last
position selected in region 1
83
2 2
1
2 2 2
1 1
2 if 2 0
2 2 if 2 0
x i x i
y i x i x i
r y r p
increment
r x r y r p

 
  
 
  
1
0 0 02
2 2 2 2 2 21
0 02
2 ( , 1)
( ) ( 1)
ellipse
y x x y
p f x y
r x r y r r
  
    

84. 1. Input rx, ry, and ellipse center (xc, yc), and obtain the
first point on an ellipse centered on the origin as
(x0, y0) = (0, ry)
2. Calculate the initial parameter in region 1 as
3. At each xi position, starting at i = 0, if p1i < 0, the
next point along the ellipse centered on (0, 0) is (xi +
1, yi) and
otherwise, the next point is (xi + 1, yi – 1) and
84
2 2 21
0 41 y x y xp r r r r  
2 2
1 11 1 2i i y i yp p r x r   
2 2 2
1 1 11 1 2 2i i y i x i yp p r x r y r     
2 2
2 2y xr x r y

85. 4. (x0, y0) is the last position calculated in region 1.
Calculate the initial parameter in region 2 as
5. At each yi position, starting at i = 0, if p2i > 0, the next
point along the ellipse centered on (0, 0) is (xi, yi – 1) and
otherwise, the next point is (xi + 1, yi – 1) and
Use the same incremental calculations as in region 1.
Continue until y = 0.
6. For both regions determine symmetry points in the other
three quadrants.
7. Move each calculated pixel position (x, y) onto the
elliptical path centered on (xc, yc) and plot the coordinate
values 85
2 2 2 2 2 21
0 0 022 ( ) ( 1)y x x yp r x r y r r    
2 2
1 12 2 2i i x i xp p r y r   
2 2 2
1 1 12 2 2 2i i y i x i xp p r x r y r     

86. 86
i pi xi+1, yi+1 2ry
2xi+1 2rx
2yi+1
0 -332 (1, 6) 72 768
1 -224 (2, 6) 144 768
2 -44 (3, 6) 216 768
3 208 (4, 5) 288 640
4 -108 (5, 5) 360 640
5 288 (6, 4) 432 512
6 244 (7, 3) 504 384
rx = 8 , ry = 6
2ry
2x = 0 (with increment 2ry
2 = 72)
2rx
2y = 2rx
2ry (with increment -2rx
2 = -128)
Region 1
(x0, y0) = (0, 6)
2 2 21
0 41 332y x y xp r r r r    
Move out of region 1 since
2ry
2x > 2rx
2y

87. 6    
5  
4 
3 
2 
1 
0 
0 1 2 3 4 5 6 7 8
87
i pi xi+1, yi+1 2ry
2xi+1 2rx
2yi+1
0 -151 (8, 2) 576 256
1 233 (8, 1) 576 128
2 745 (8, 0) - -
Region 2
(x0, y0) = (7, 3) (Last position in region 1)
1
0 22 (7 ,2) 151ellipsep f   
Stop at y = 0

88. • Definition
• Line Attribute
• Curve Attribute
• COLOR AND GRAY SCALE LEVEL
• AREA FILLED ATTRIBUTE
• Text and Characters
30/9/2008 Lecture 2 88

89. 30/9/2008 Lecture 2 89
Definition
Parameter that affects the way a primitive will be
displayed
Line Attribute
. Type
. Width
. Color
. Pen & Brush

90. 30/9/2008 Lecture 2 90
Type
. Solid
. Dotted – very short dash with spacing equal
to
or greater than dash itself
. Dashed – displayed by generating an
interdash spacing
Pixel count for the span and interspan length is
specified
by the mask . Ex. 111100011110001111
Note : Fixed pixel with dashes can produce unequal length

91. 30/9/2008 Lecture 2 91
Width
. Specify in pixels and proportion of a standard line width.
. Thicker line can be produced by.
. Adding extra pixel vertically when |m| < 1
. Adding extra pixel horizontally when |m| > 1
. Issues:
. Line have different thickness on the slope
. Problem with
. End of the line
. Joining the two lines (polygon)

92. 30/9/2008 Lecture 2 92
Width

93. 30/9/2008 Lecture 2 93

94. 30/9/2008 Lecture 2 94

95. Pen and Brush
. The selected “pen” or “brush” determine the way a line will be drawn.
. Pens and brushes have size, shape, color and pattern attribute.
. Pixel mask is applied in both of them.
30/9/2008 Lecture 2 95

96. Similar to line : type + width
Thicker curves can be produced by:
1. Plotting additional pixel
2. Filling the space between two concentric circles.
3. Using thicker pen or brush
30/9/2008 Lecture 2 96

97. 30/9/2008 Lecture 2 97
Width

98. Color
Colors are represented by colors codes which are
positive integers.
Color information is stored in frame buffer or in
separate table and use pixel values as index to the
color table.
Two ways to store color information :
1. Direct
2. Indirect
30/9/2008 Lecture 2 98

99. Direct
30/9/2008 Lecture 2 99

100. Indirect
30/9/2008 Lecture 2 100

101. Exercise:
What is the size of frame buffer required for the following cases:
Case 1 (Direct): Resolution of 1024 * 1024 with 24 bits per
pixel
Case 2 (Indirect): Same resolution with 8 bit per pixel that
indexed out of 16 million available colors
Conclusion
CLUT is good for storage but cant give a very high resolution picture.
30/9/2008 Lecture 2 101

102. 30/9/2008 Lecture 2 102

103. 30/9/2008 Lecture 2 103

104. .Apply for monitor that have no color
.Shades of grey (white->light grey->dark grey->black)
.Color code mapped onto grayscale codes
.2 bits can give 4 level of grayscale
.8 bits per pixel will allow 256 combination
.Dividing the actual code with 256 will give range of 0 and 1
Ex:
Color code in color display is 118
To map to nearest grayscale then
118/256 = 0.45
 light gray
30/9/2008 Lecture 2 104

105. 30/9/2008 Lecture 2 105
. Option for filling a defined region is whether solid , pattern and
colors.
Fill Styles
. Three basic fill styles are:
. hollow with color border.. interior color is same with
background

106. 30/9/2008 Lecture 2 106
. filled with a solid color .. color up to and including the border
pattern .. control by other table

107. 30/9/2008 Lecture 2 107

108. 30/9/2008 Lecture 2 108
. Color-Blended Fill Region
-Soft-fill
- P = tF + (1-t)B where 0 < t < 1
If t < 0.5 , background color contributes more to
the interior color of the region than does the fill
color.

109. 30/9/2008 Lecture 2 109

110. 30/9/2008 Lecture 2 110

111. 30/9/2008 Lecture 2 111

112. 30/9/2008 Lecture 2 112

113. 30/9/2008 Lecture 2 113

114. 30/9/2008 Lecture 2 114
Text and Characters
•Very important output primitive
• Many pictures require text
• Two general techniques used
– Bitmapped (raster)
– Stroked (outline)

115. 30/9/2008 Lecture 2 115
Each character represented (stored) as a 2-D array
– Each element corresponds to a pixel in a
rectangular “character cell”
– Simplest: each element is a bit (1=pixel on, 0=pixel
off)
00111000
01101100
11000110
11000110
11111110
11000110
11000110
00000000

116. 30/9/2008 Lecture 2 116
Each character represented (stored) as
a series of line segments
– sometimes as more complex primitives
Parameters needed to draw each stroke
– endpoint coordinates for line segments

117. 30/9/2008 Lecture 2 117
Characteristics of Bitmapped Characters
• Each character in set requires same amount of
memory to store
• Characters can only be scaled by integer scaling
factors
• "Blocky" appearance
• Difficult to rotate characters by arbitrary angles
• Fast (BitBLT)
Characteristics of Stroked Characters
• Number of stokes (storage space) depends on
complexity of character
• Each stroke must be scan converted more time to
display
• Easily scaled and rotated arbitrarily
• – just transform each stroke

118. 30/9/2008 Lecture 2 118
When each function reference a single attribute that specify exact
how primitive to be displayed ; then its called
individual (unbundled attribute).
.Bundled attributes is where a set of attributes value can be chos
by specifying the appropriate index table.
.The table for each primitive that defines group of attribute values
called bundled table.
.Attribute that can be bundled are:
. Bundled Line Attribute
. Bundled Area-Fill Attribute
. Bundled Text Attribute
. Bundled Marker Attribute