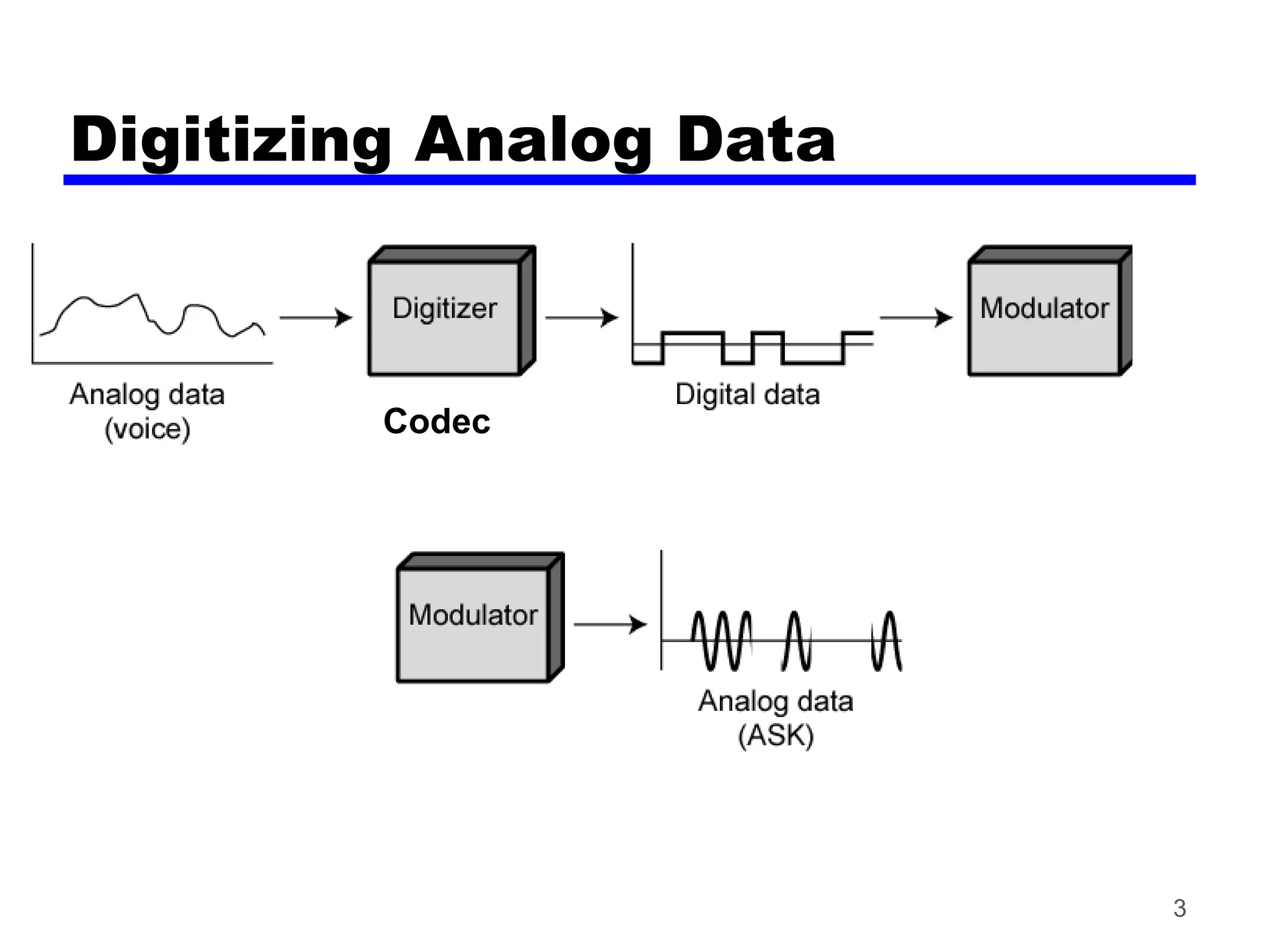
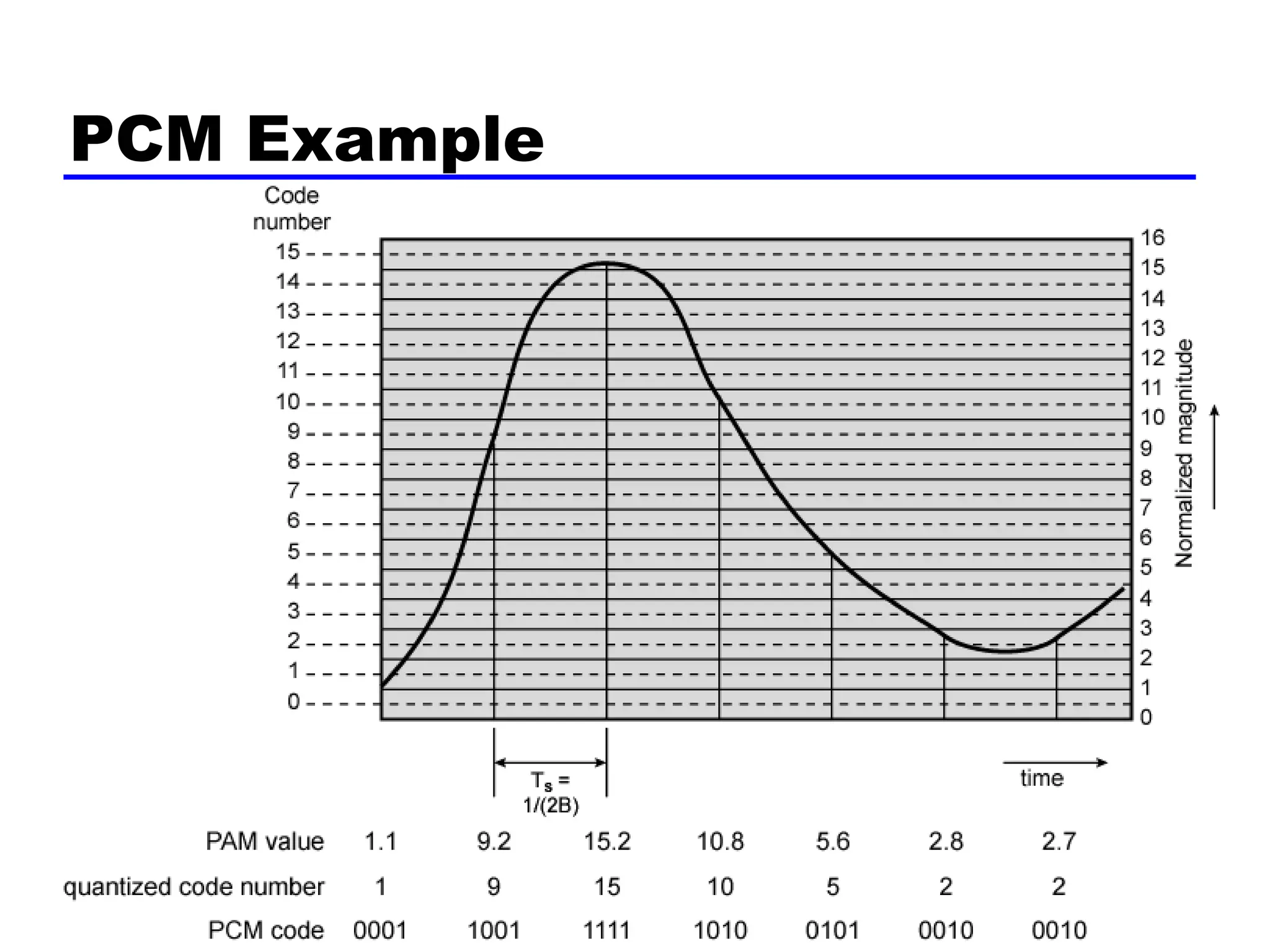
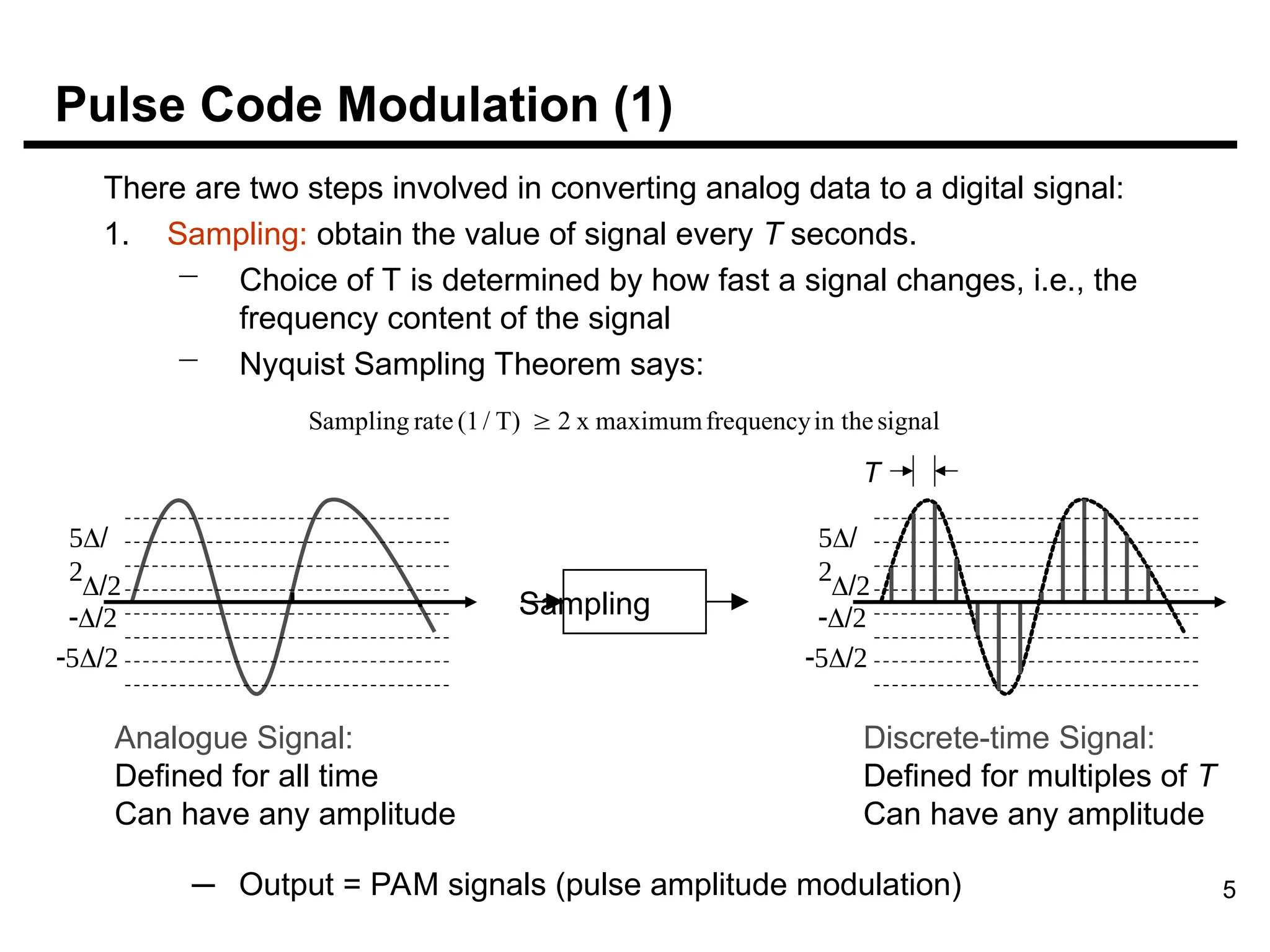
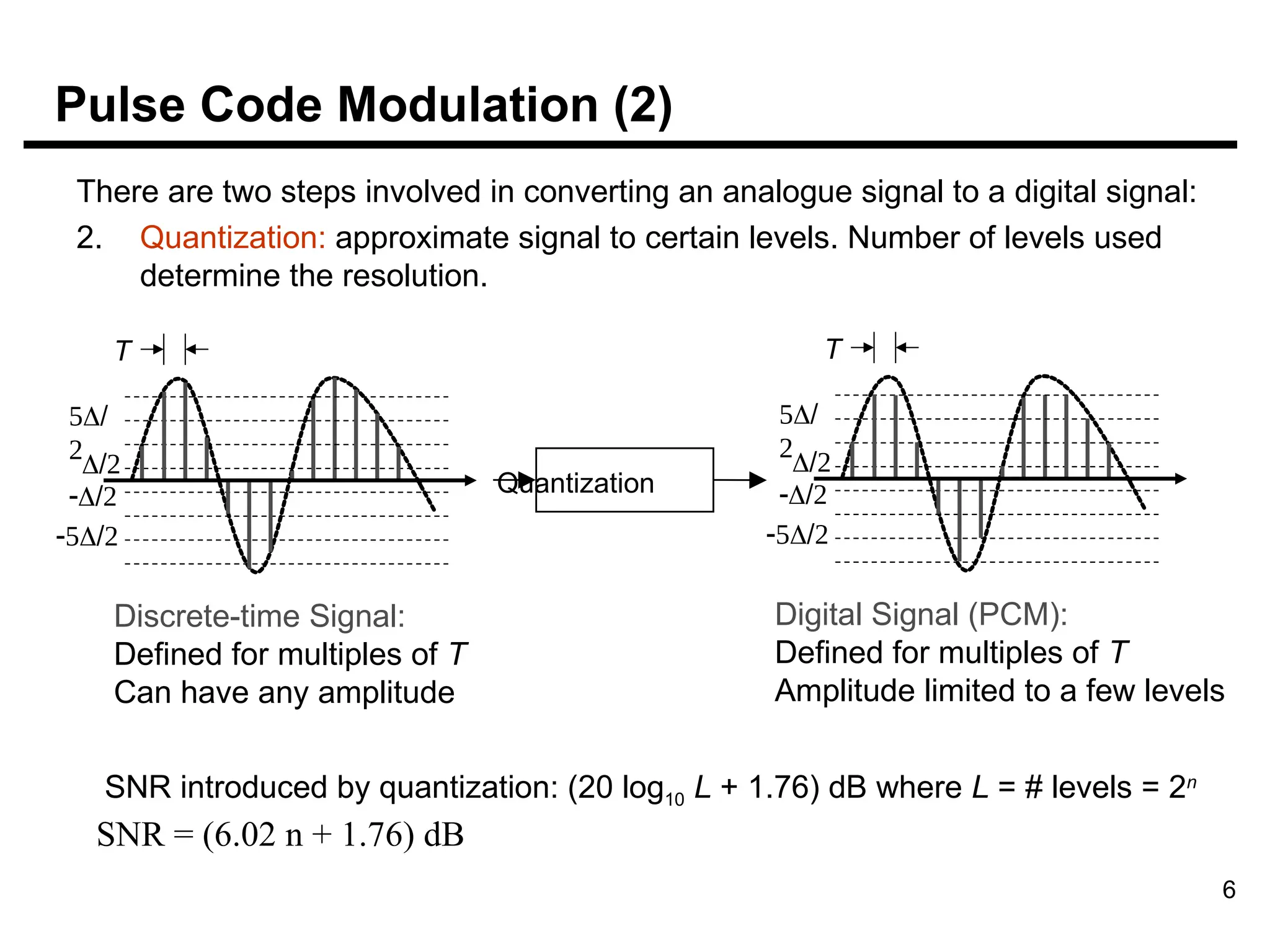
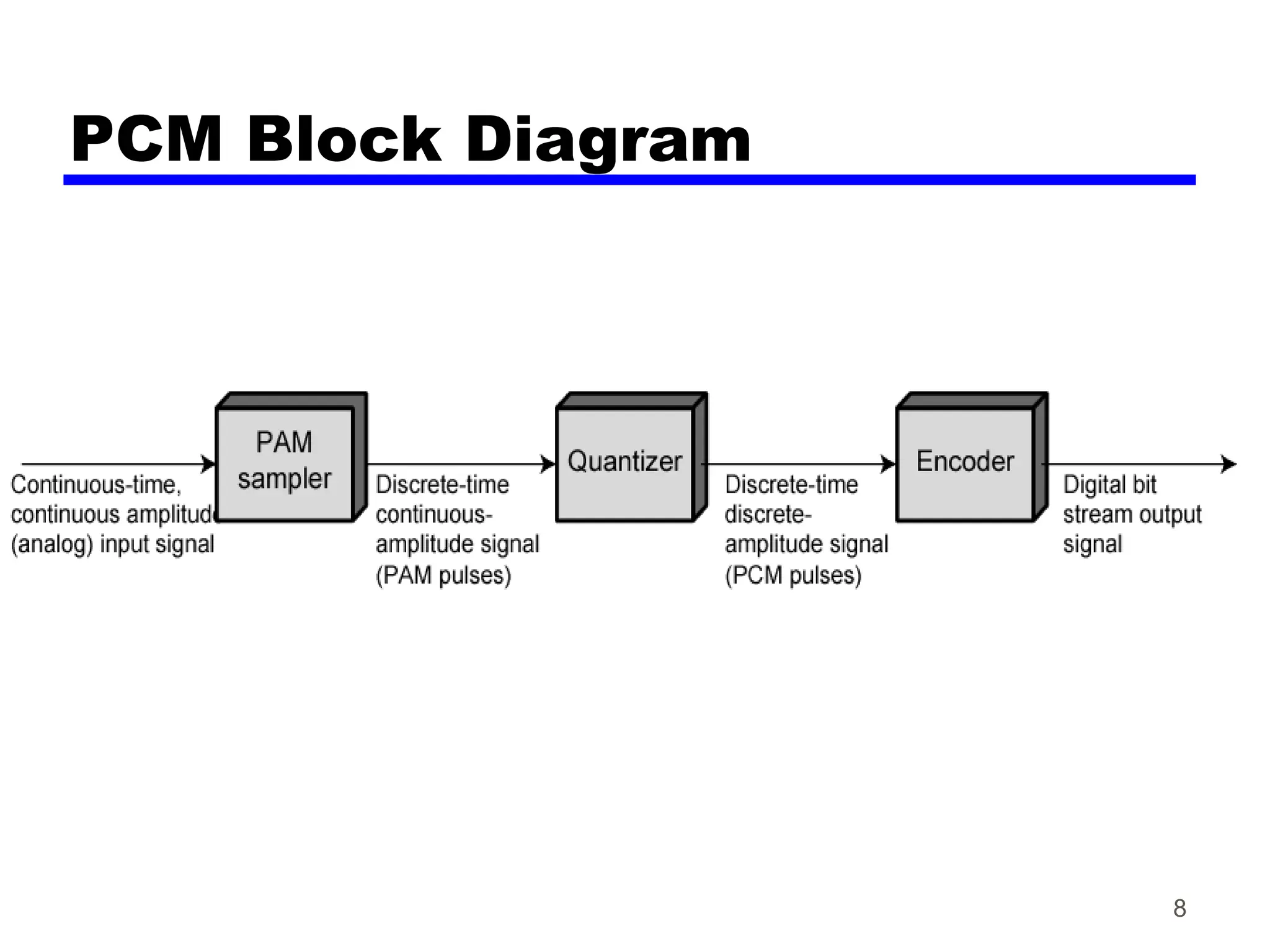
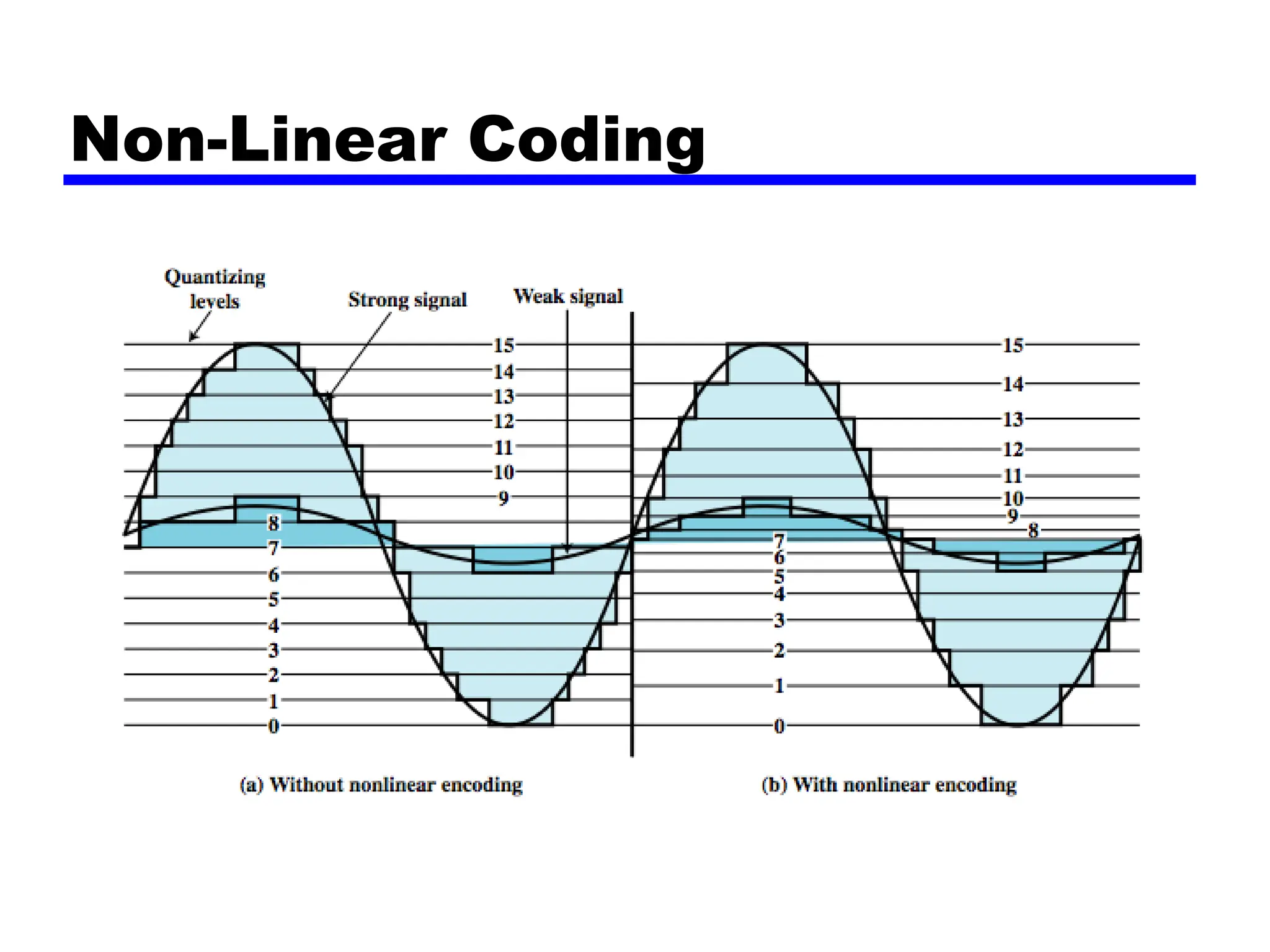
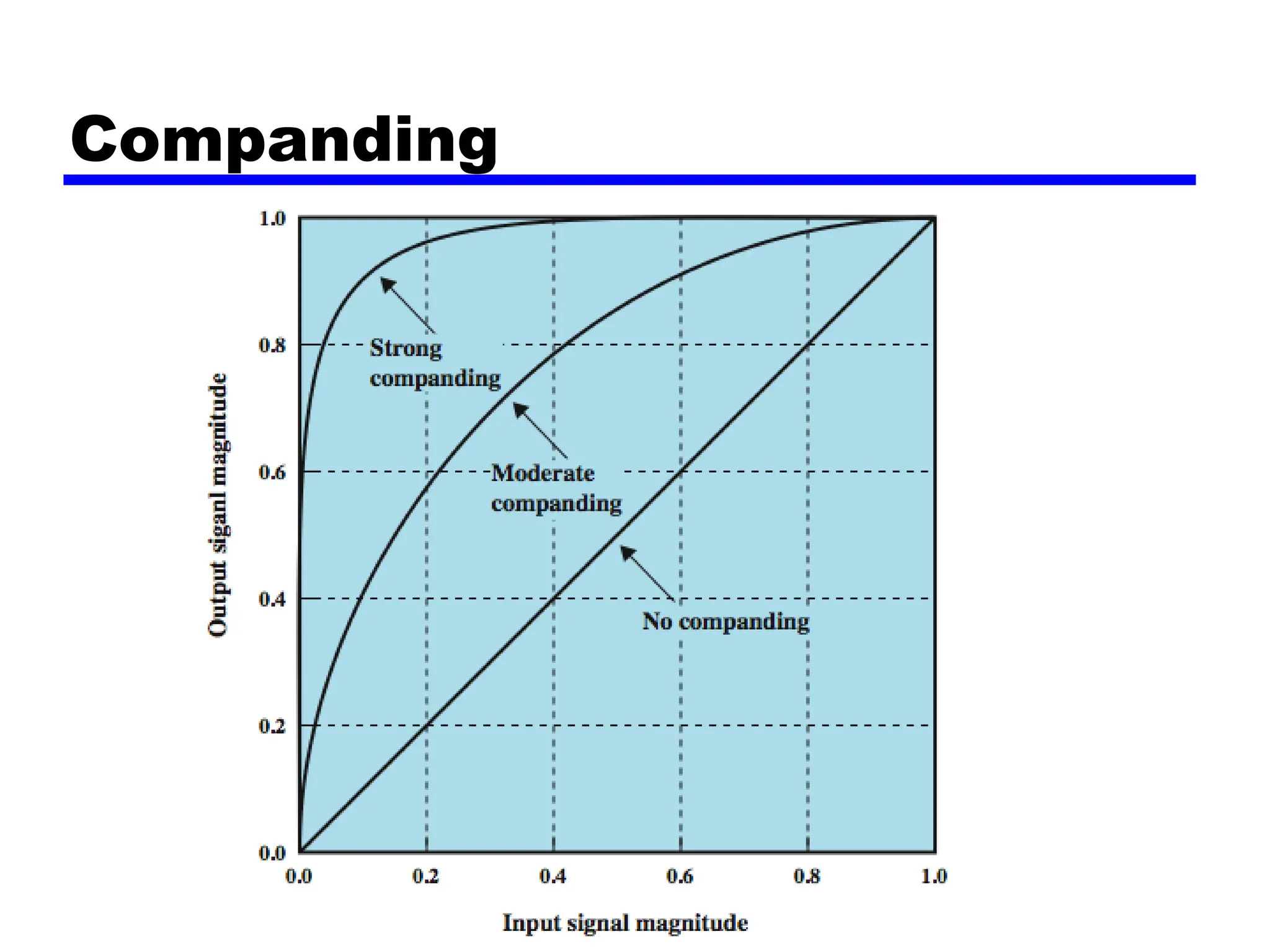
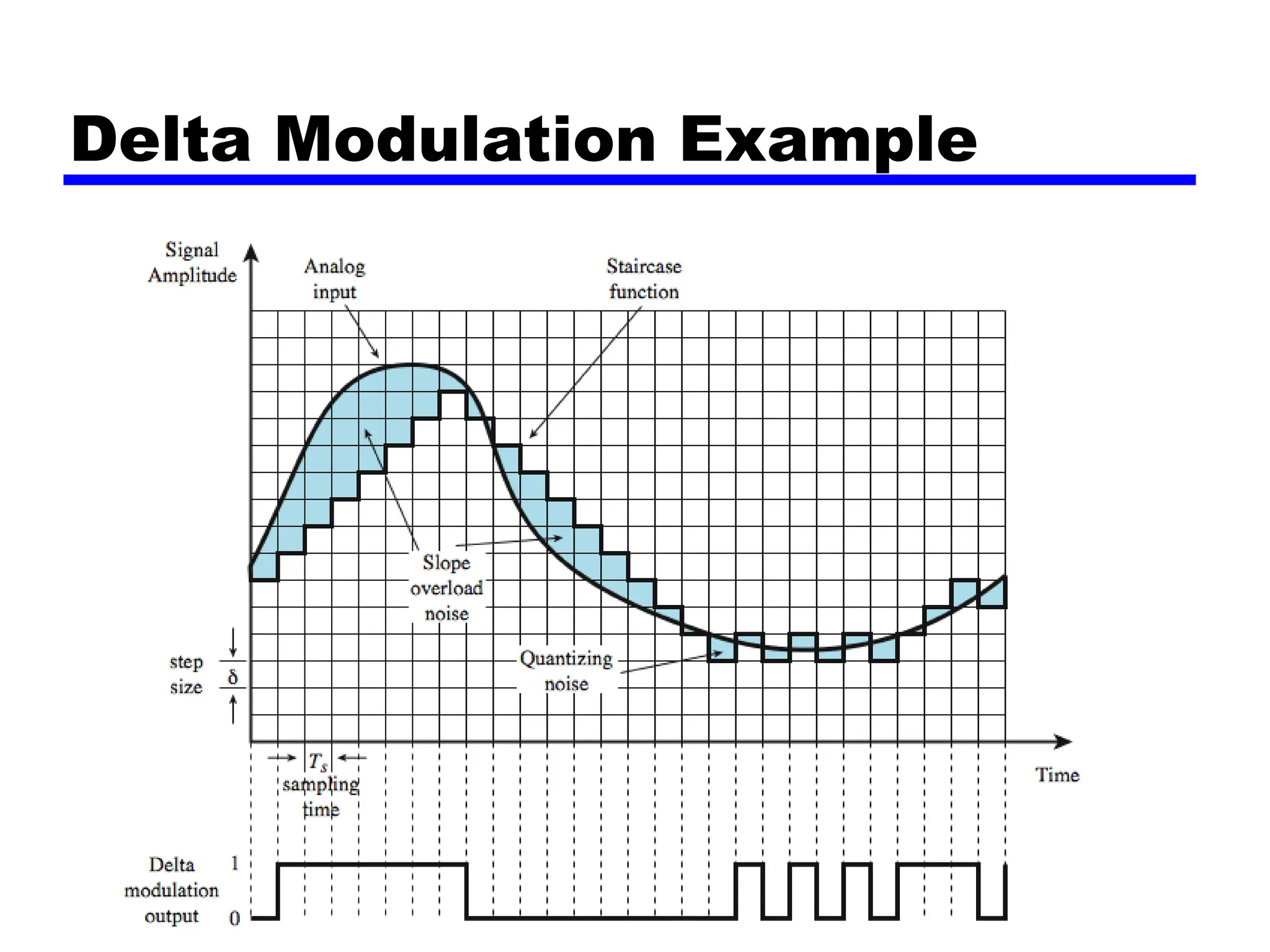
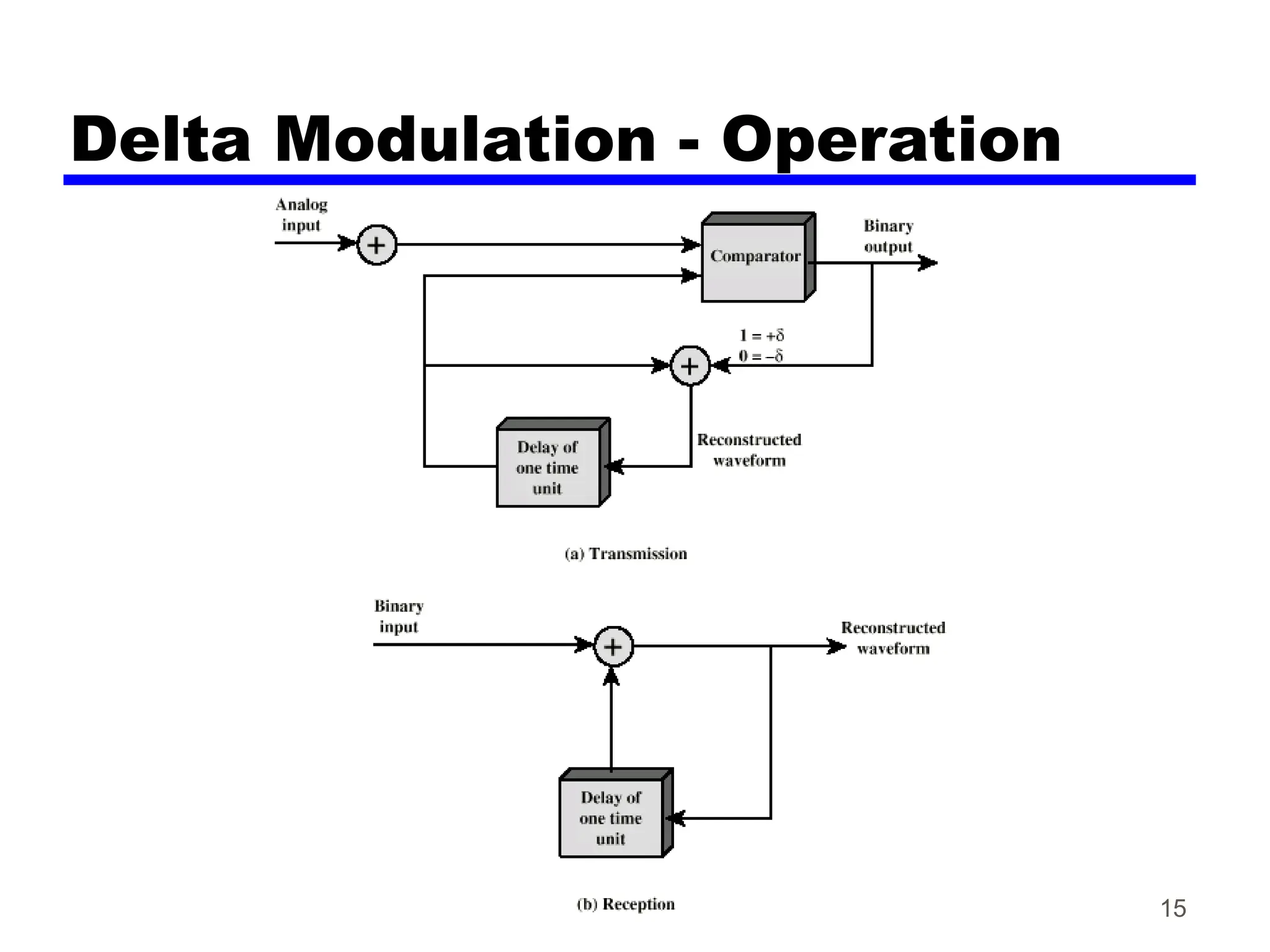
The document discusses the process of digitizing analog data into digital signals through techniques such as Pulse Code Modulation (PCM) and Delta Modulation. It explains key concepts, including sampling, quantization, and the Nyquist sampling theorem, which ensures that sampled signals retain the original information when done correctly. Additionally, it compares the complexities and signal-to-noise ratios of PCM and Delta Modulation while highlighting the advantages of digital transmission methods over analog.