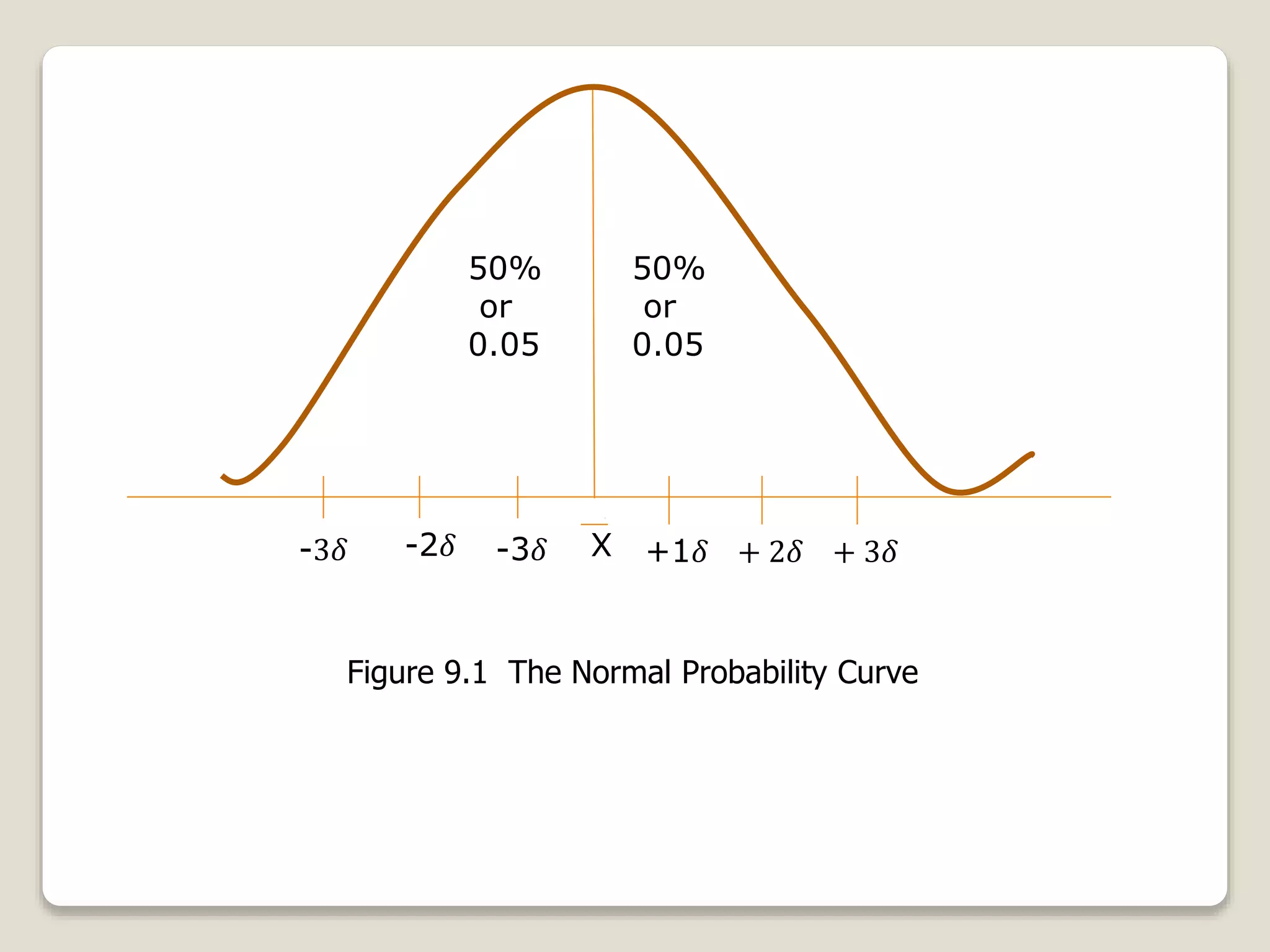
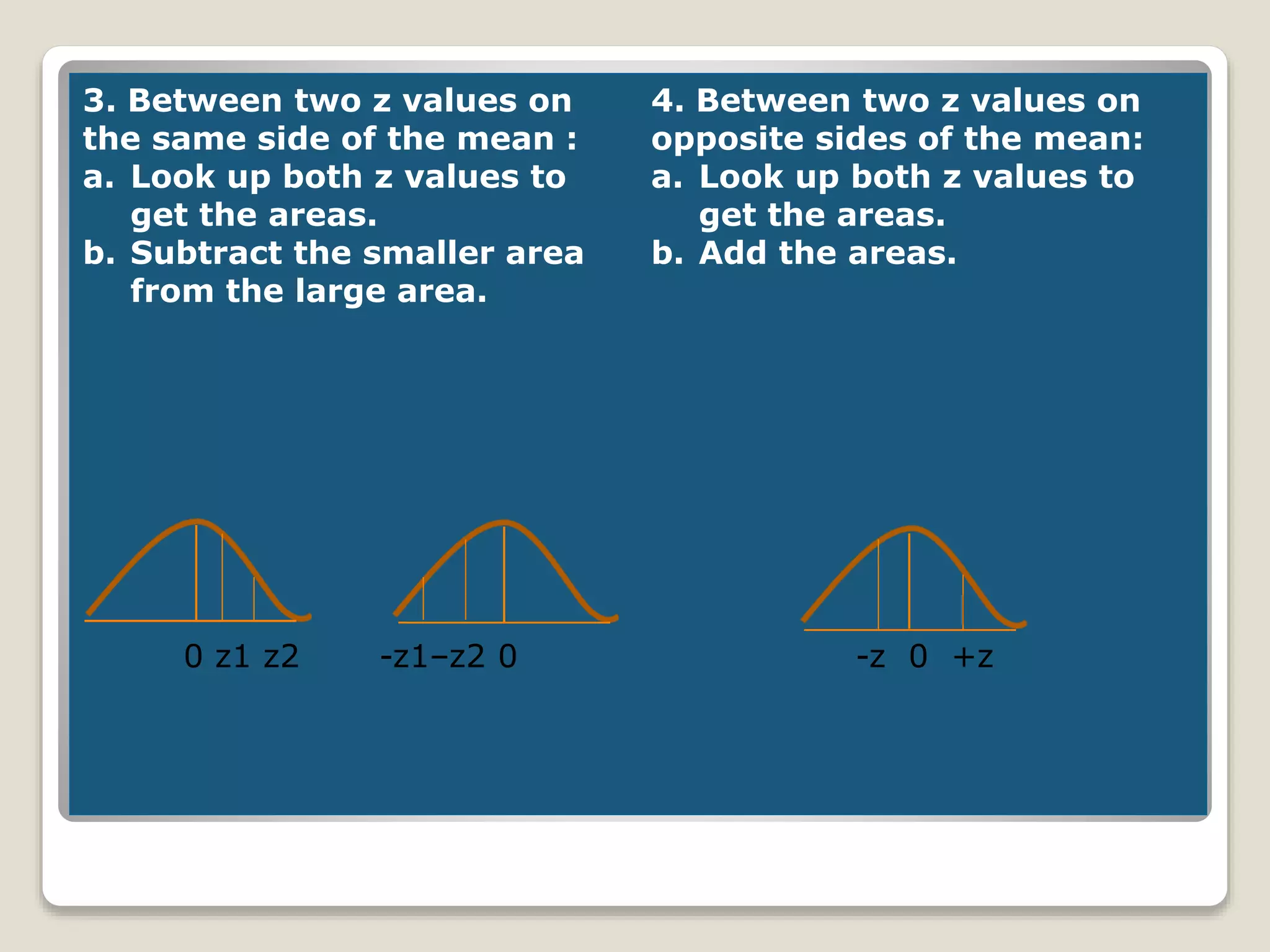
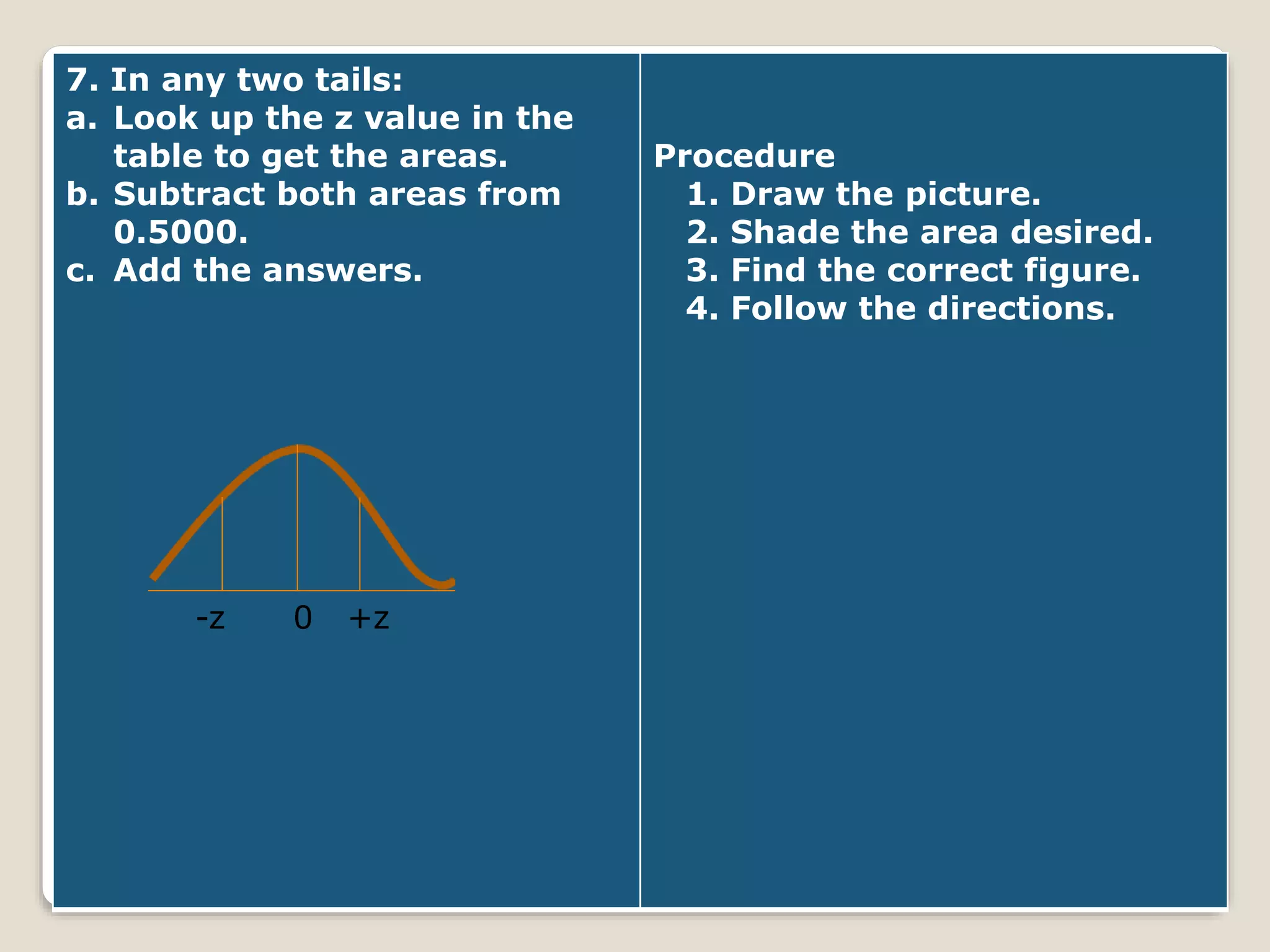
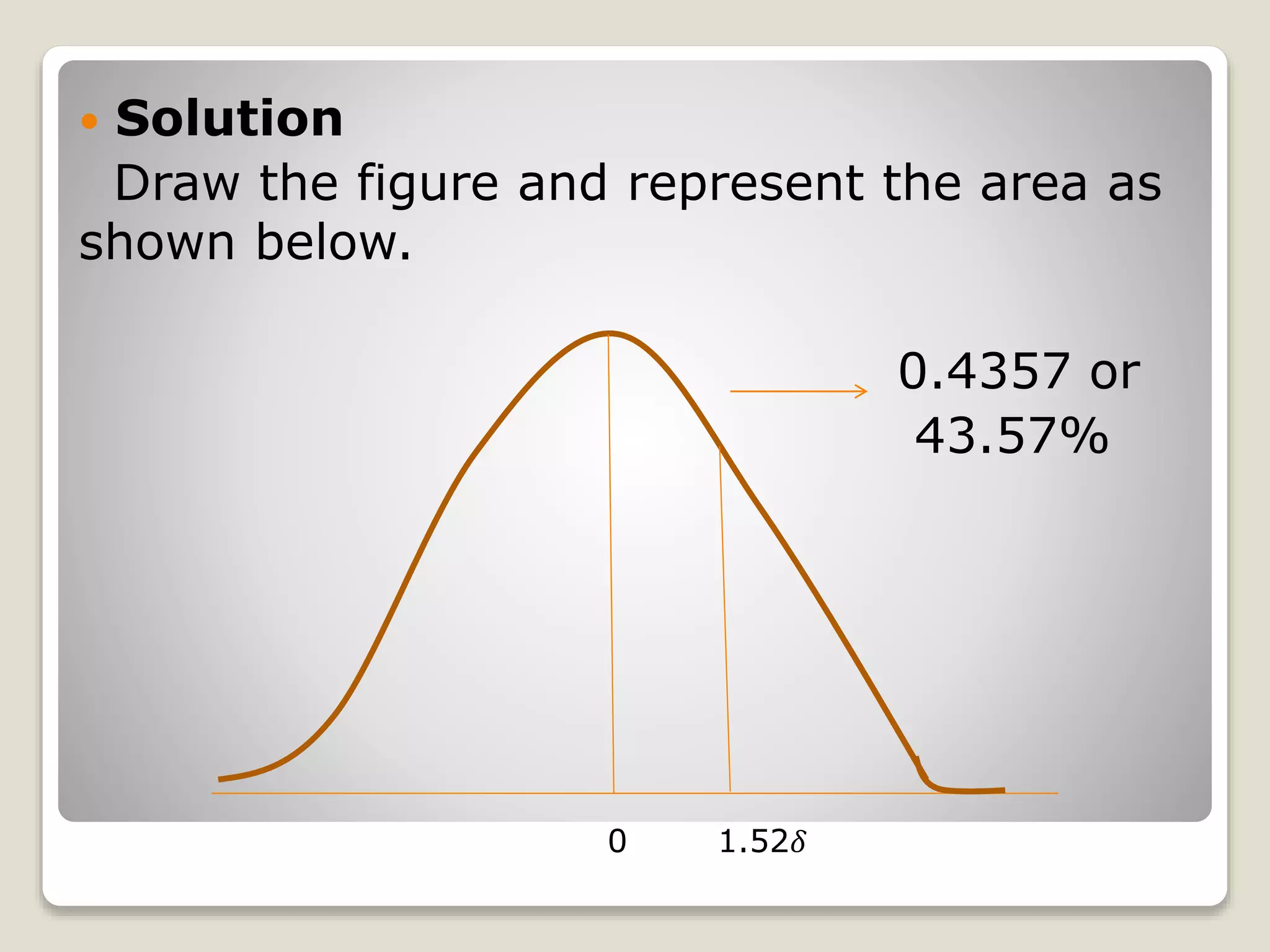
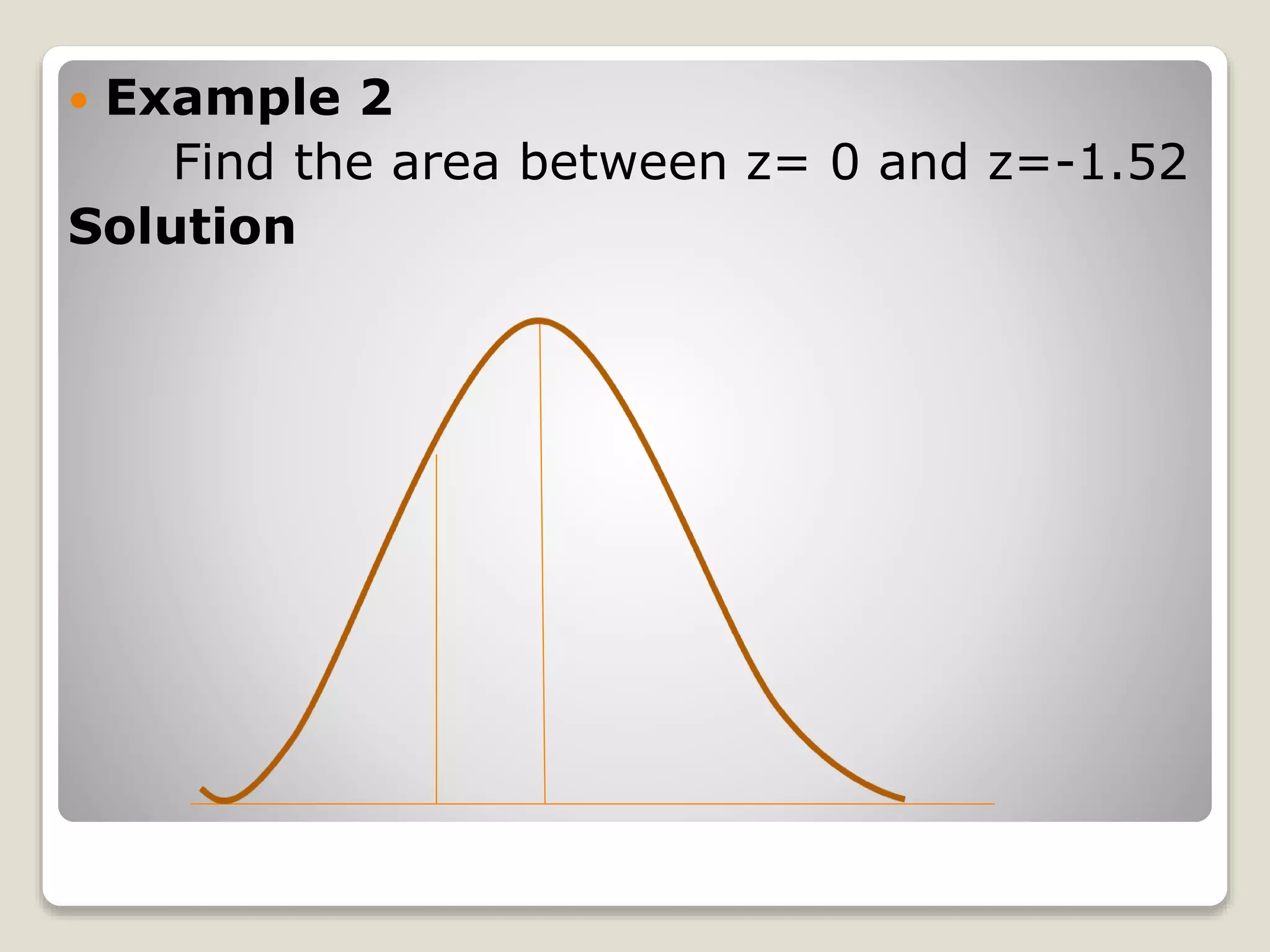
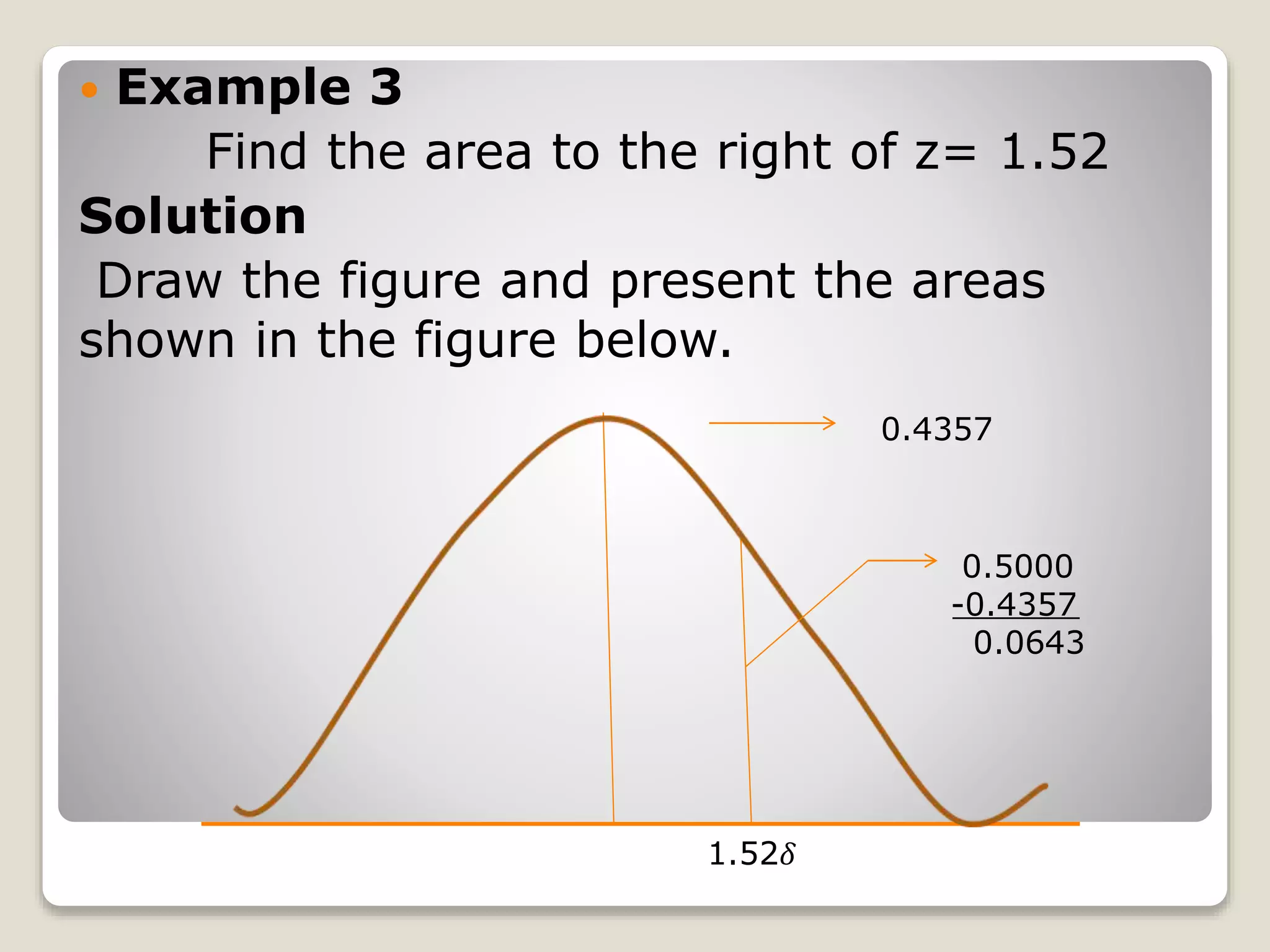
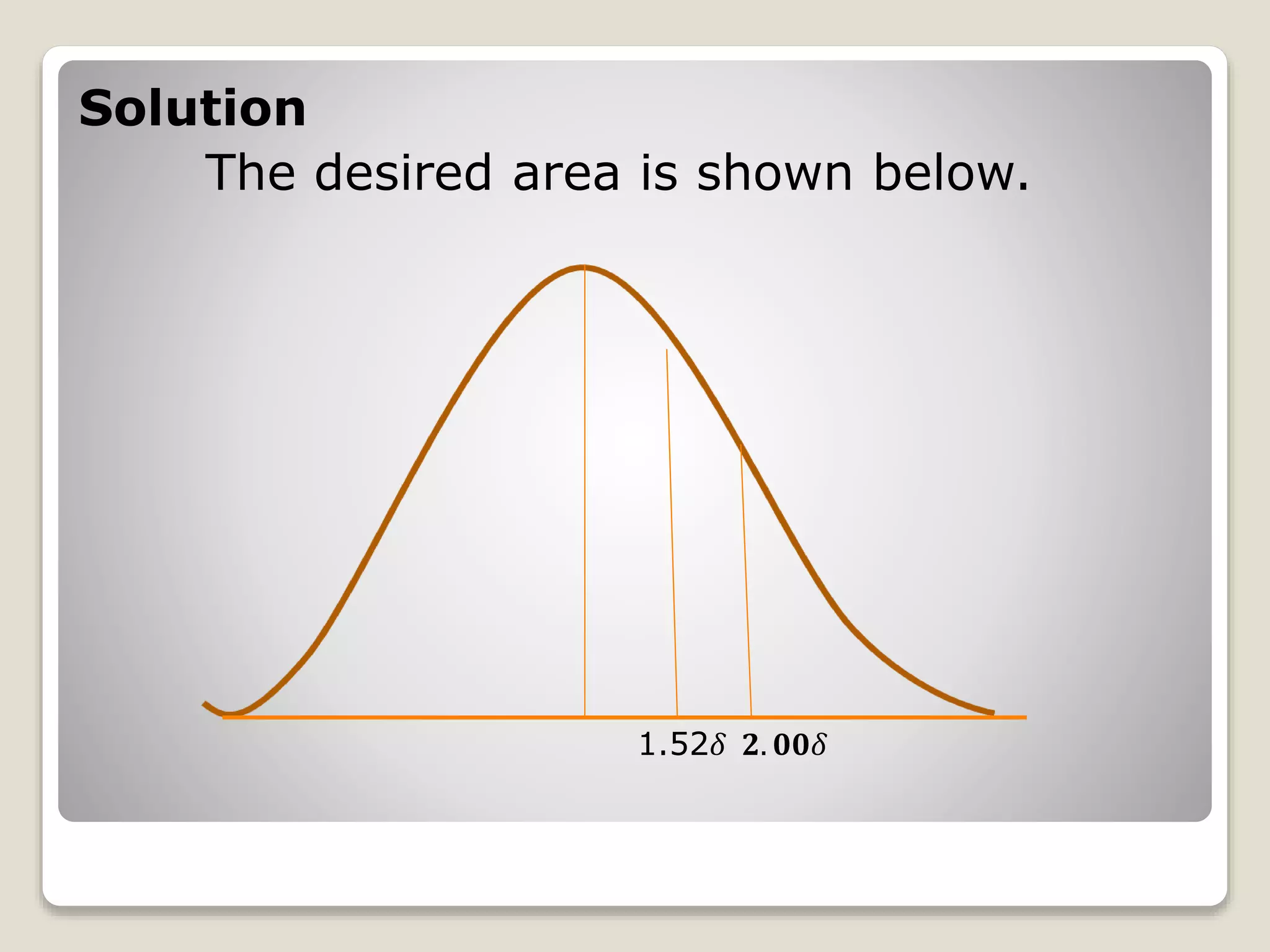
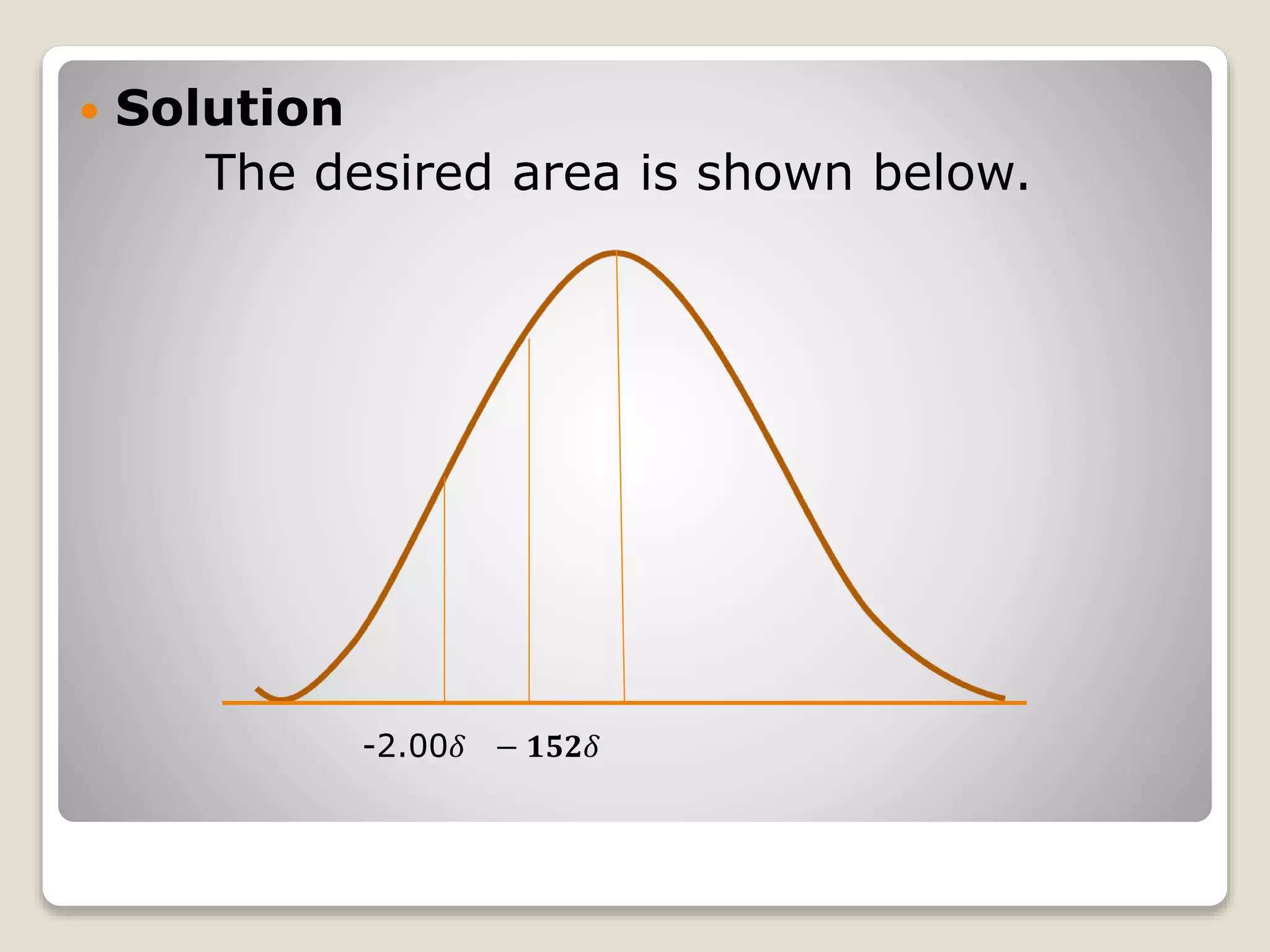
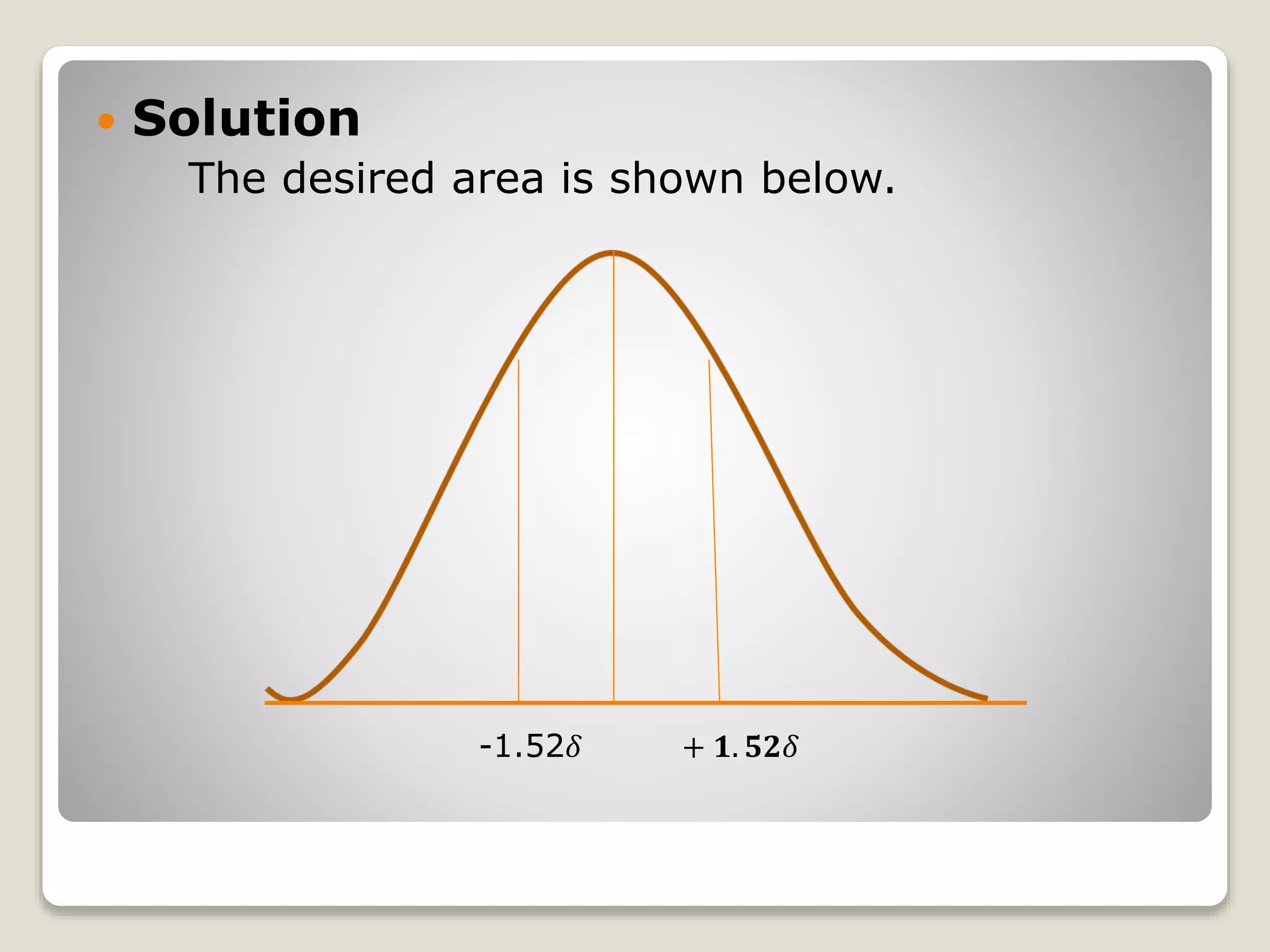
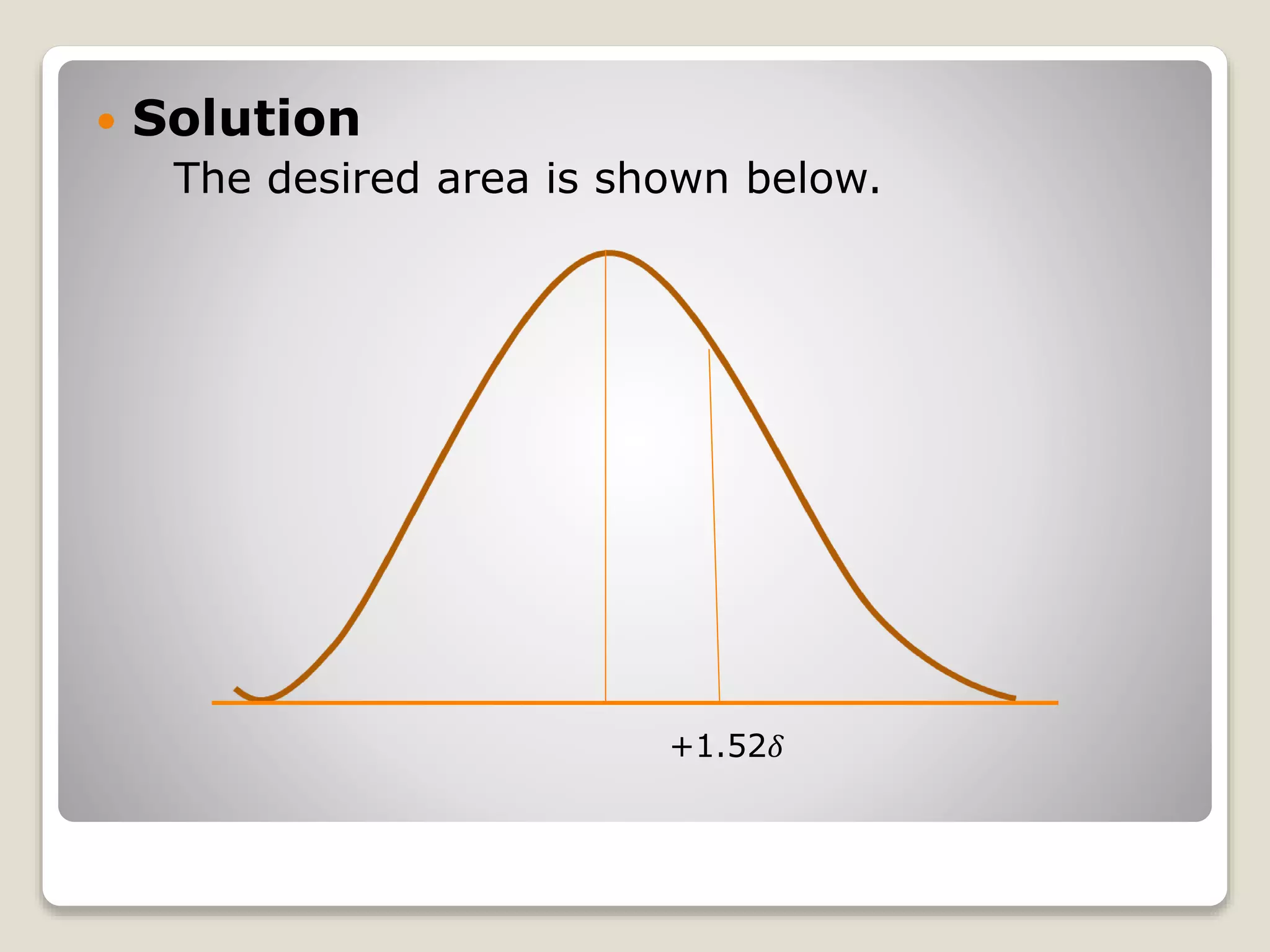
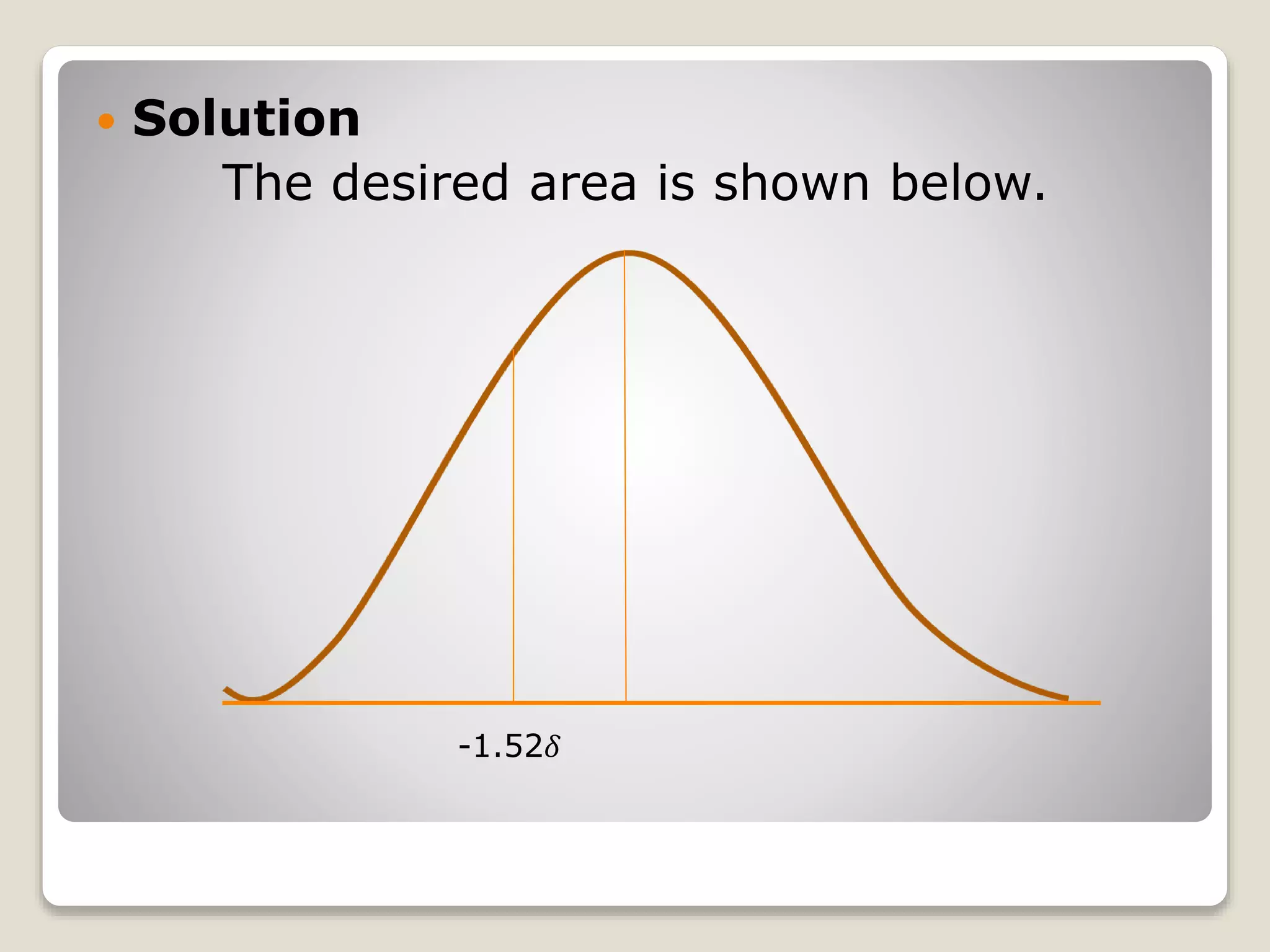
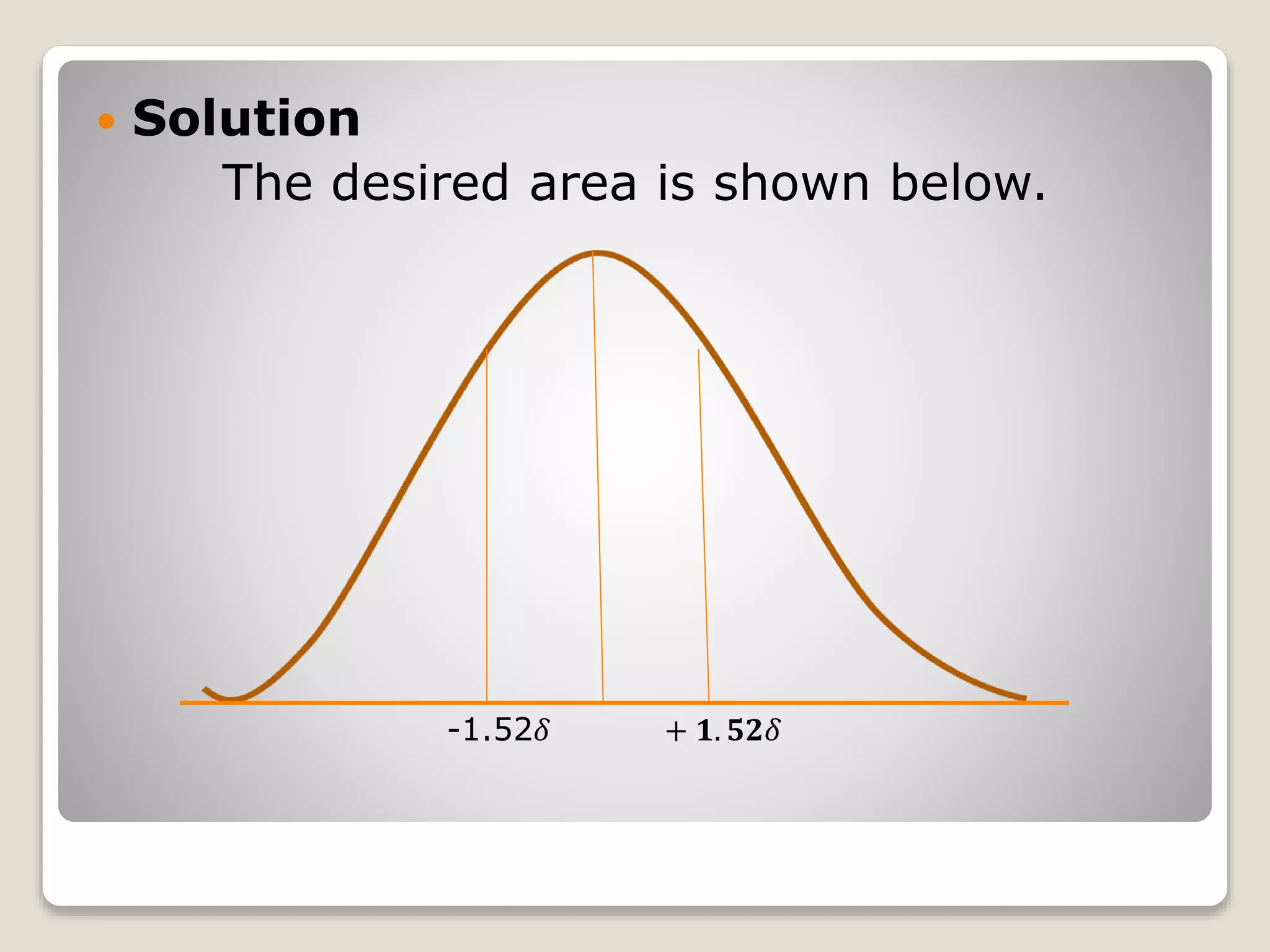
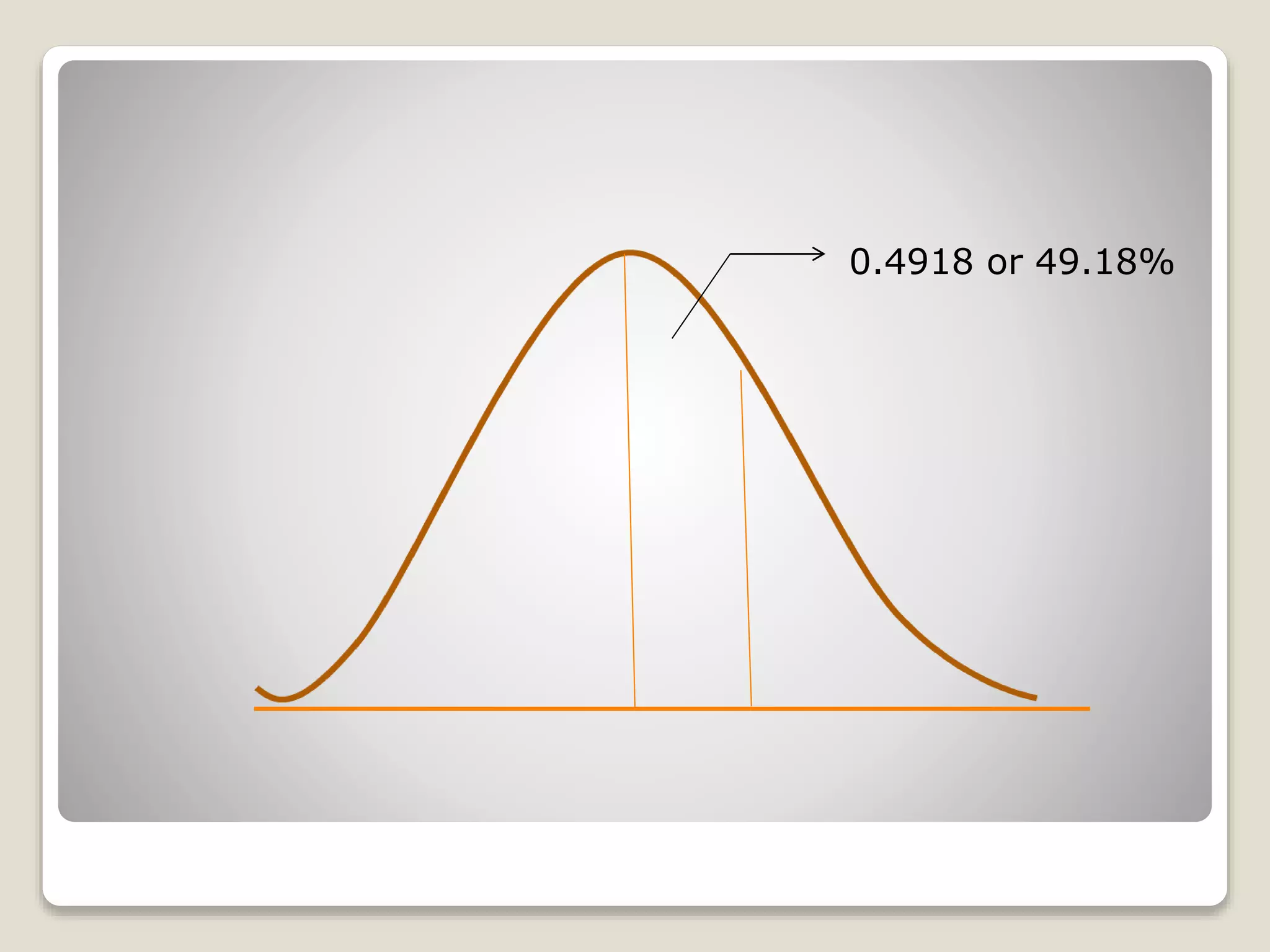
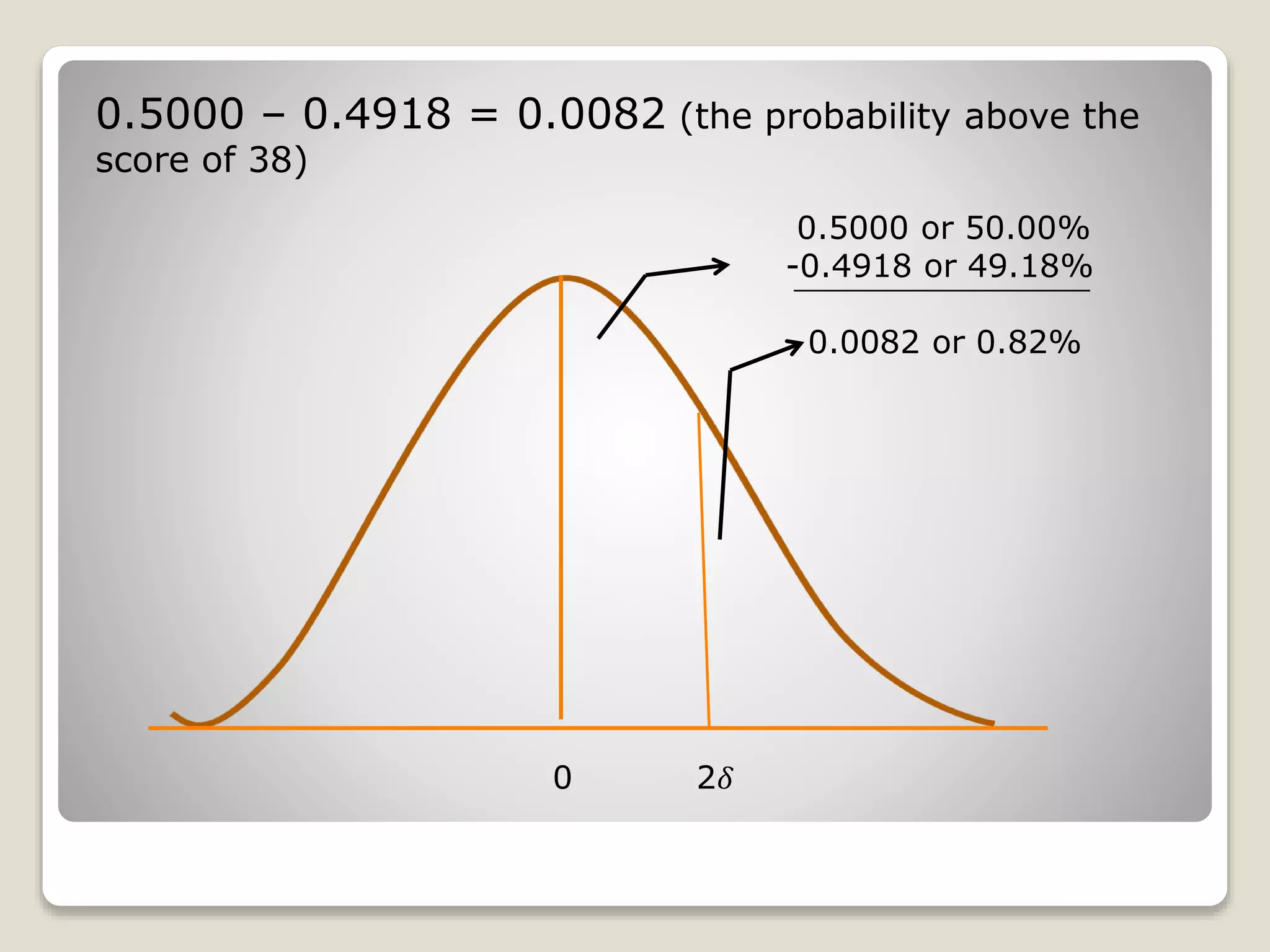
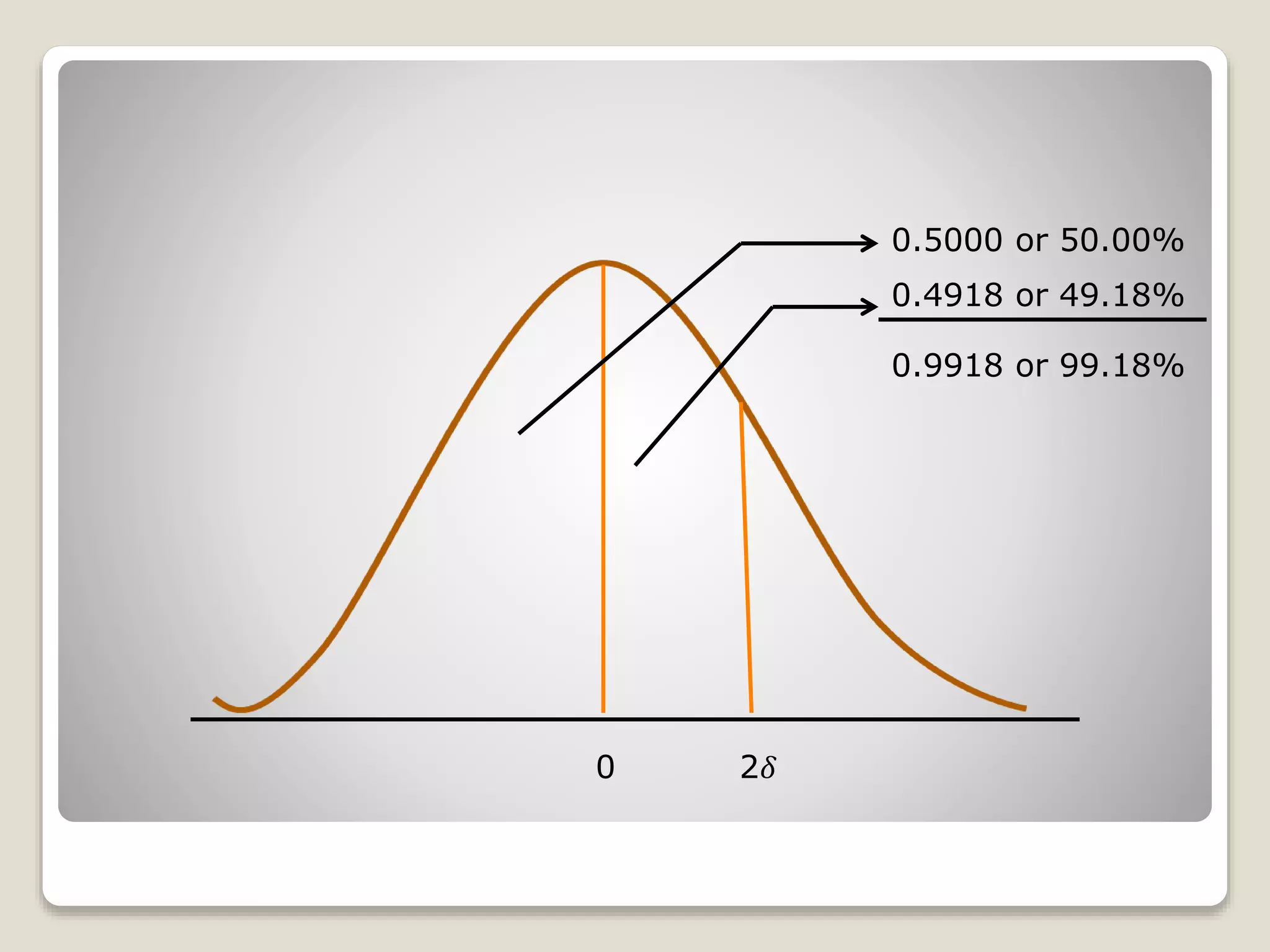
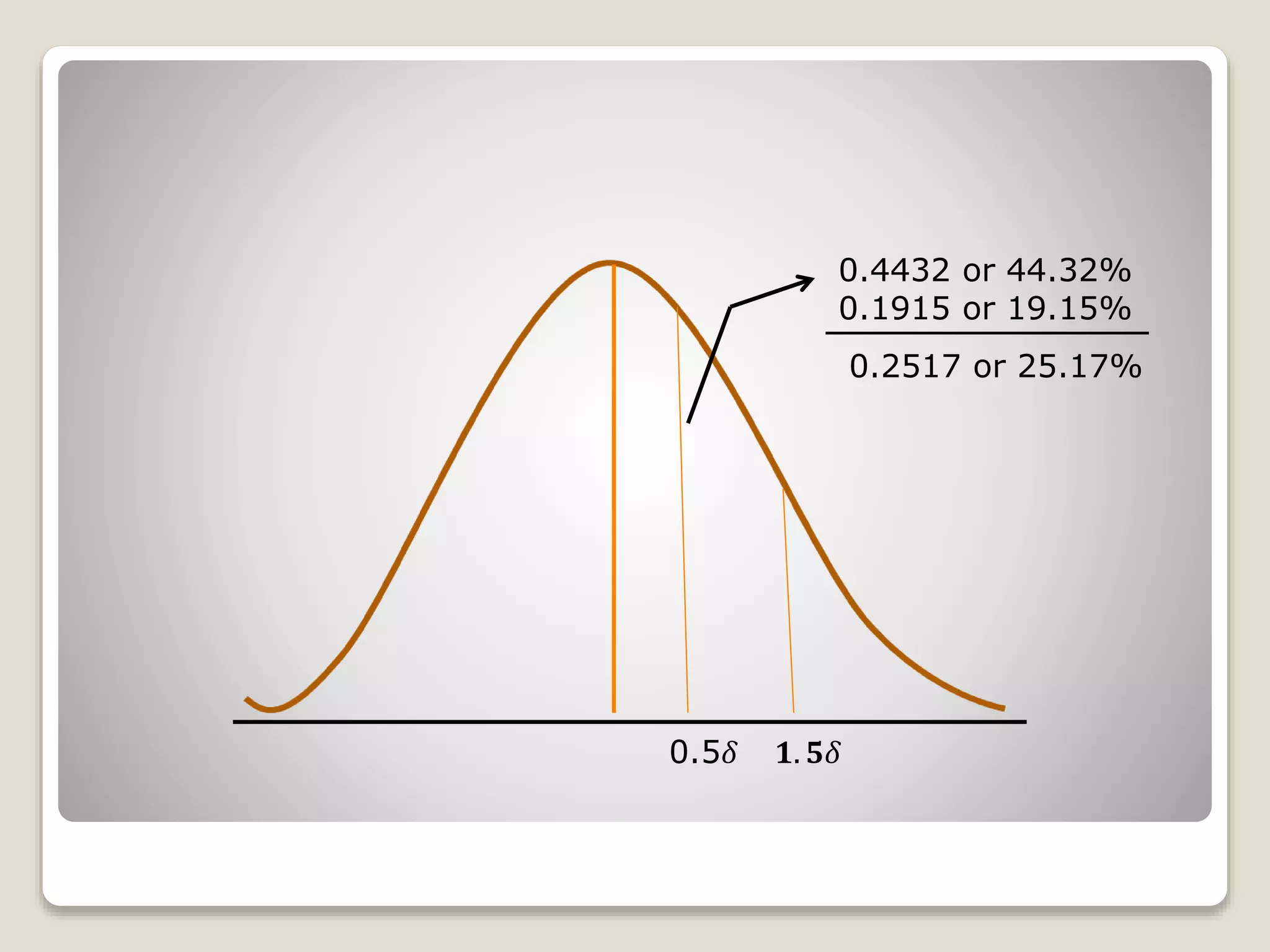
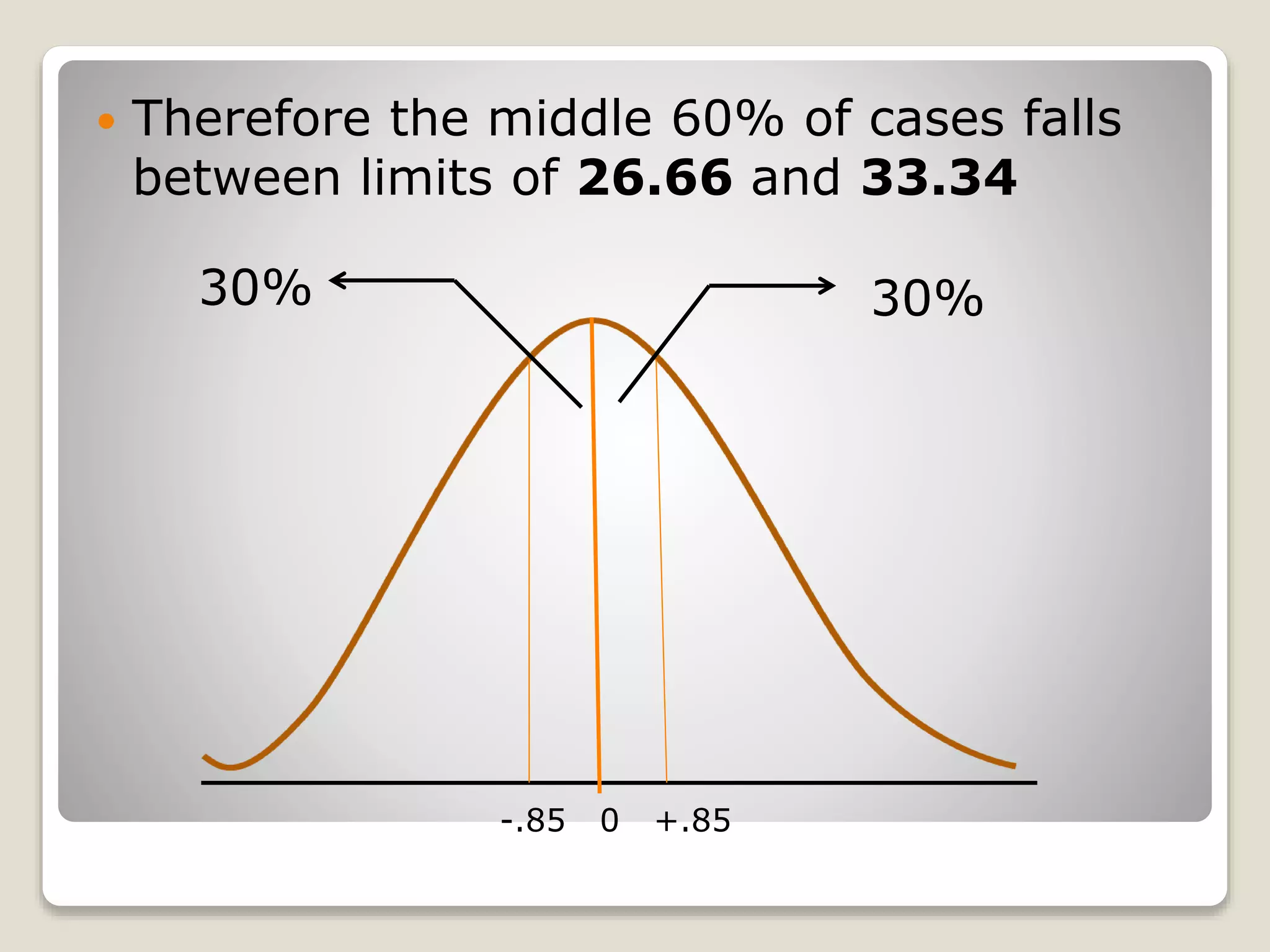
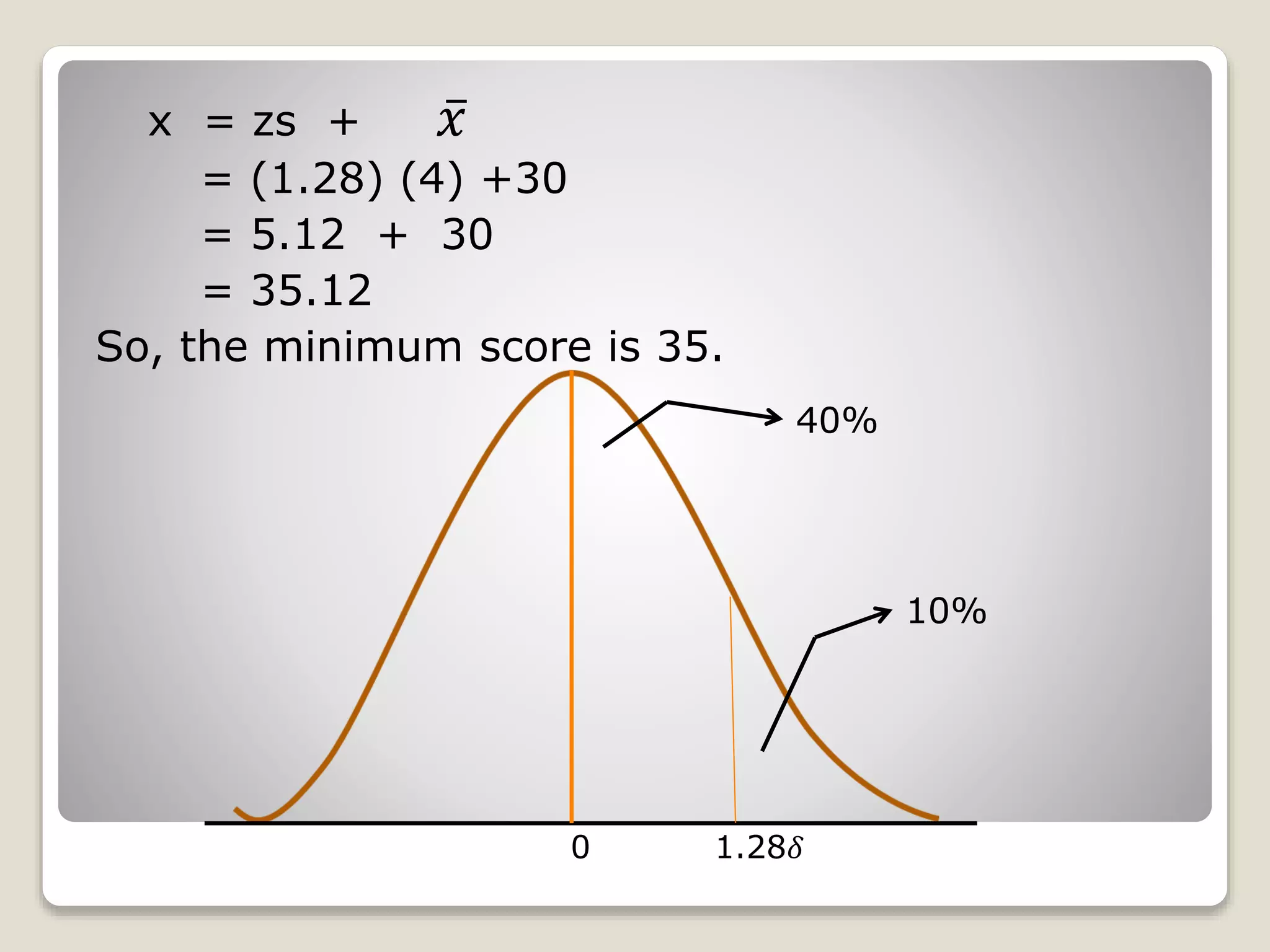
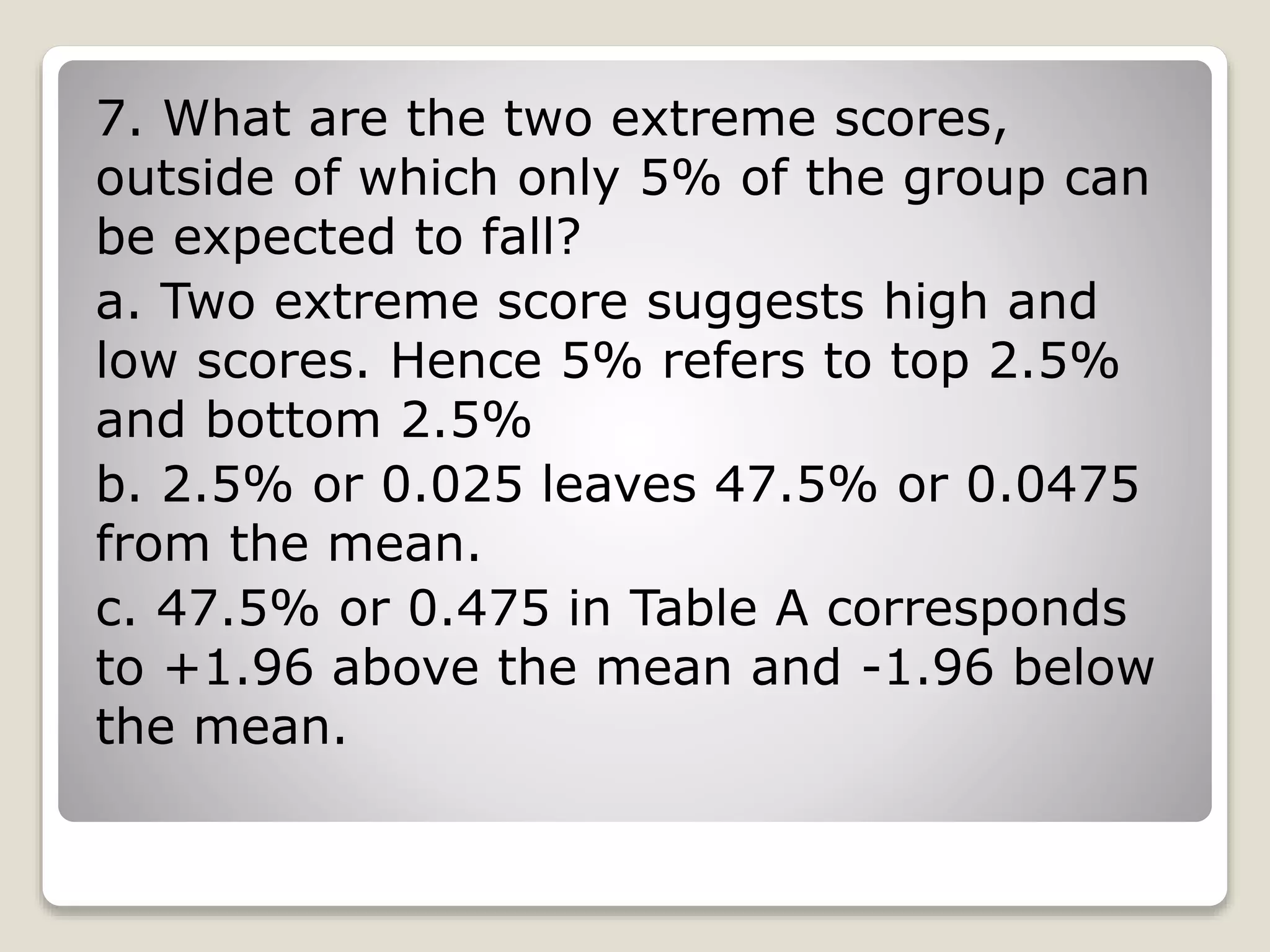
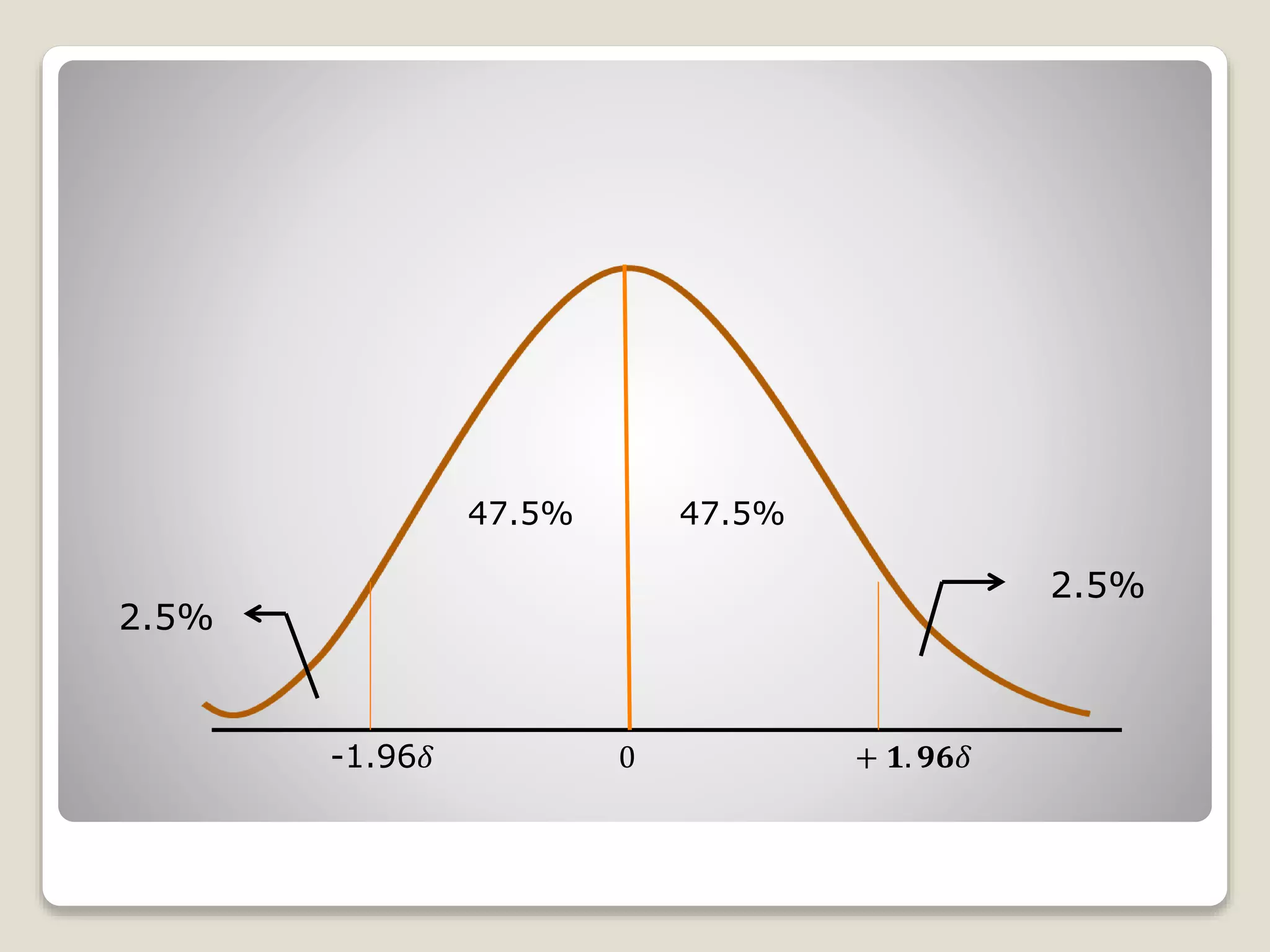
The document discusses the normal distribution curve and how to calculate probabilities and areas under the normal curve. It defines the normal curve, its key properties like symmetry and bell shape, and how it can be used to describe distributions. It then provides examples of how to calculate areas under the normal curve in different situations, such as between two z-scores, in the tails, or between z-scores on opposite sides of the mean. The examples demonstrate how to convert scores to z-scores and look up areas in tables to calculate probabilities.

1. Chapter 9
THE NORMAL CURVE
DISTRIBUTION
Prepared by :
Nenevie D. Villando

2. Learning Objectives
 By the end of this chapter, you will be able
to:
1.Define and explain the concept of
the normal curve.
2.Convert empirical scores to Z scores
and use Z scores and the normal
curve table to find areas above,
below and between points on the curve.
3. Express areas under the curve in
terms of probabilities.

3.  Uses of the Normal Curve
1. The normal curve can be used for
describing distribution of scores.
2. The normal curve can be used in
interpreting the standard deviation.
3. The normal curve can be used in
making statements of probability.
4.The normal curve is an essential
ingredient of statistical decision making,
whereby the researcher generalizes her or
his results from sample to populations.

4.  Summary of the Properties of the
Theoretical Normal Distribution
1.The normal distribution curve is bell-
shaped.
2. The mean, median, and mode are equal
and located at the center of the
distribution.
3. The normal curve is unimodal (i.e., it has
only one mode).
4. The curve is symmetrical about the mean, which
is equivalent to saying that its shape is the same
on both sides of a vertical line passing through the
center.

5. 5. The curve is continuous – i.e., there are
no gaps or holes. For each value of X, there
is a corresponding value of Y.
6. The curve never touches the x axis.
Theoretically, no matter how far in either
direction the curve extends, it never meets
the X axis- but it gets increasingly closer.
This is so, because N is infinite.
7. The total area under the normal
distribution curve is equal to 1.00, or
100%.

6. 8. The area under the normal distribution
curve that lies within one standard
deviation of the mean is approximately
0.68 or 68%; within two standard
deviations, about 0.95 or 95%; and within
three standard deviations about 0.997, or
99.7%.
9. The basic unit of measurement is
expressed in sigma unit (𝛿) or standard
deviations along the baseline. The sigma
units are called the z-scores.

7. 10. Two parameters are used to describe
the curve. One is the parameter mean,
which is equal to zero, and the other is the
standard deviation, which is equal to 1.
11. Standard deviation or z-scores
departing away from the mean towards the
right of curve or above the mean are
expressed in positive values, while the
scores departing from the mean to the left
of the curve or below the mean are in
negative values.

8. 50%
or
0.05
-3𝛿 -2𝛿 -3𝛿 X +1𝛿 + 2𝛿 + 3𝛿
Figure 9.1 The Normal Probability Curve
50%
or
0.05

9.  Areas under the Normal Curve
In making use of the properties of the
normal curve to solve certain types of
statistical problems, one must learn how to
find areas under the normal curve.
Steps to follow in Finding Areas under
the Standard Normal Distribution
Curve :
Step 1 Draw a picture.

10. Step 2 Shade the area desired.
Step 3 Find the correct figure in the
following procedure table.
Step 4 Follow the directions given in the
appropriate block of the procedure table to
get the desired area.

11.  Procedure Table
Finding the Area under the Normal
Distribution Curve
1. Between 0 and any z
value: Look up the z value
in the table to get the
area.
2. In any tail :
a. Look up the z value to get
the area.
b. Subtract the area from
0.5000.
0 +z -z 0 0 +z -z 0

12. 3. Between two z values on
the same side of the mean :
a. Look up both z values to
get the areas.
b. Subtract the smaller area
from the large area.
4. Between two z values on
opposite sides of the mean:
a. Look up both z values to
get the areas.
b. Add the areas.
0 z1 z2 -z1–z2 0 -z 0 +z

13. 5. To the left of any z value,
where z is greater than the
mean:
a. Look up the z value to get
the area.
b. Add 0.5000 to the area.
6. To the right of any z value,
where z is less than the mean:
a. Look up the z value in the
table to get the area.
b. Add 0.5000 to the area.
0 +z -z 0

14. 7. In any two tails:
a. Look up the z value in the
table to get the areas.
b. Subtract both areas from
0.5000.
c. Add the answers.
Procedure
1. Draw the picture.
2. Shade the area desired.
3. Find the correct figure.
4. Follow the directions.
-z 0 +z

15.  Situation 1 Find the area under the
normal curve between 0 and any z value.
Example 1
Find the area under the normal
distribution curve between z= 0 and z= 1.5

16.  Solution
Draw the figure and represent the area as
shown below.
0.4357 or
43.57%
0 1.52𝛿

17. Since Table A gives the area
between 0 and any z value to the
right of 0.,one need only to look up
the z value in the table. Find 1.5 in
the left column and 0.02 in the top
row. The value where the column and
row meet in the table is the answer.

18. .4357
Z .00 .01 .02 .03 .04 .05 .07 .08 .09
0.0
0.1
0.2
1.3
1.4
1.5
1.6

19.  Example 2
Find the area between z= 0 and z=-1.52
Solution

20. Table A does not give the areas for
negative values of z. But since the normal
distribution is symmetric about the mean, the
area to the left of the mean is the same as
the area to the right of the mean. Hence one
need only to look up the area for z= +1.52,
which is 0.4357 or 43.57%
 Note : Remember that area is always a
positive number, even if the z value is
negative.
Situation 2 Find the area under the normal
curve in either tail.

21.  Example 3
Find the area to the right of z= 1.52
Solution
Draw the figure and present the areas
shown in the figure below.
0.4357
0.5000
-0.4357
0.0643
1.52𝛿

22.  Example 4
Find the area to the left of z= -1.52
Solution
The desired area is shown below.
-1.52𝛿

23.  Again Table A gives the area for positive z
values. But from the symmetric property
of the normal distribution, the area to the
left of -1.52 is the same as the area to
the right of +z= 1.52. You will notice that
the area will be derived as in example 3,
0.0643.
Situation 3 Find the area between z=1.52
and z=2.00
 Example 5
Find the area between z=1.52 and
z=2.00

24. Solution
The desired area is shown below.
1.52𝛿 𝟐. 𝟎𝟎𝛿

25. ◦ For this situation, look up the area from
z=0 to z=2.00 and the area from z=+1.52
. Then subtract the two areas. From Table
A, the areas from z=0 to z=2.00 is 0.4772
and the area from z=0 to z=1.52 is
0.4357. Subtract the two areas and the
resulting area is 0.0415.
Example 6
Find the area between z=-1.52 and
-2.00

26.  Solution
The desired area is shown below.
-2.00𝛿 − 𝟏𝟓𝟐𝛿

27.  In this case the same result 0.0415 will be
obtained since the normal curve is
symmetrical meaning the half of the curve
is 0.5000 and the other half is also 0.5000
irregardless of whether they are located
below or above the mean.
Situation 4 Find the area under the curve
between any two z values on opposite sides
of the mean.
Example 7
Find the area between z=+1.52 and
z=-1.52

28.  Solution
The desired area is shown below.
-1.52𝛿 + 𝟏. 𝟓𝟐𝛿

29.  Now, since the two areas are on opposite
sides of z=0, one must find both areas
and add them. The area between z=0 and
z=1.52 is 0.4357. The area between z=0
and z= -1.52 is also 0.4357. Hence, the
total area between z= +1.52 and z=-1.52
is 0.4357+0.4357=0.8714 or 87.14%.
Situation 5 Find the area under the curve
to the left of any z value, where z is greater
than the mean.
Example 8
Find the area to the left of z=+1.52

30.  Solution
The desired area is shown below.
+1.52𝛿

31.  Since Table A gives only the area between
z=0 and z=+1.52, one must add 0.5000
to the table area, since 0.5000 (half) of
the area lies to the left to z=0. The area
between z=0 and z=+1.52 is 0.4357, and
the total area is 0.4357+0.5000=0.9357.
Situation 6 Find the area under the
normal curve to the right of any z value,
where z is less than the mean.
Example 9
Find the area to the right of z=-1.52

32.  Solution
The desired area is shown below.
-1.52𝛿

33.  In this case, the same result will be
obtained as in example 8 since the normal
curve is symmetrical and z=0 to z=-1.52
is 0.4357+0.5000, the half of the area,
then the total area to the right of z=-1.52
is 0.9357.
Situation 7 Find the total area under the
curve of any two tails.
Example 10
Find the area to the right of z=+1.52
and to the left of z= -1.52

34.  Solution
The desired area is shown below.
-1.52𝛿 + 𝟏. 𝟓𝟐𝛿

35.  The area to the right of z=+1.52 is
0.5000- 0.4357= 0.0643. The area to the
left of z=-1.52 is also 0.0643 since the
same area was used. The total area, then,
is 0.4357+0.4357=0.8714 or 87.14%.
Application of the Normal Probability Curve
In a mathematics test, with a sample
of 50 students, the mean score is 30 and
standard is 4.0. Assuming that the
distribution is normal.

36. 1. What percentage of the students falls
between the mean and the score of 38?
2. What is the probability that a score
picked at random will lie above the score
of 38?
3. What is the probability that a score will
lie below score of 38?
4. How many cases fall between scores of
32 and 36?

37. 5. What limits will include the middle 60%
of cases?
6. What is the minimum score a pupil
should get to belong to the upper 10% of
the group?
7. What are the two extreme scores,
outside of which only 5% of the group can
be expected to fall?

38.  Solutions
1. What percentage of the pupils falls
between the mean and the score of 38?
a. Convert raw score to z-score.
z = 𝑥- 𝑥 = 38 – 30 = 8 = 2.0
b. Refer to the table for areas under the
normal curve in Appendix A.
z= 2 corresponds to 0.4918
S 4 4

39. c. Convert 0.4918 to percent: 0.4918=
49.18%
So the percentage of the pupils
that falls between the mean and the
score of 38 is 49.18%.

40. 0.4918 or 49.18%

41. 2. What is the probability that a score
picked at random will lie above the score of
38?
a. Convert raw score to z-score.
z= x – x = 38 -30 = 8 = 2.0
b. z=2 corresponds to 0.4918 in the
table in Table A.
S 4 4

42. c. 0.4918 is the proportion of the area from
the mean to z=2. What we are interested in
this problem is the area above z=2, so get
the proportion of the area above z=2.
d. We know that the proportion of the area
above the mean is 0.5000, so to determine
the area above z=2 , we should subtract
0.4918 from 0.5000

43. 0.5000 – 0.4918 = 0.0082 (the probability above the
score of 38)
0.5000 or 50.00%
-0.4918 or 49.18%
0.0082 or 0.82%
0 2𝛿

44. 3. What is the probability that a score will
lie below score of 38?
a. Convert raw score to z-score
z= x – x = 38 -30 = 8 = 2.0
b. z=2 corresponds to 0.4918 in Table A.
c. Proportion below the mean is 0.5000
plus the proportion from the mean to z=2
which is 0.4918= 0.9918 (probability below
the score of 38).

45. 0.5000 or 50.00%
0.4918 or 49.18%
0.9918 or 99.18%
0 2𝛿

46. 4. How many cases fall between scores of
32 and 36?
a. Convert each score to z-score
z= x – x = 32 -30 = 2 = 0.50
z= x – x = 36 -30 = 6 = 1.50
b. From Table A
z= 0.50 = 0.1915 z= 1.50= 0.4432

47. c. Since we are looking for the area between z=
0.50 which is 0.1915 and z= 1.50 which is 0.4432
what we are going to do is to subtract 0.1915 from
0.4432.
0.4432- 0.1915= 0.2517 since we are looking
for the cases that falls within this area and the
resulting value is 0.2517, we need to convert this
into percent and round it off to a whole number
because we are dealing with pupils. Therefore, the
number of cases is 25. This means that there are
25 students with scores between 32 and 36
including 32 and 36,respectively.

48. 0.4432 or 44.32%
0.1915 or 19.15%
0.2517 or 25.17%
0.5𝛿 𝟏. 𝟓𝛿

49. 5. What limits will include the middle 60%
of cases?
a. Divide 60% into 2. That gives 30%
below the mean and 30% above the
mean.
b. From Table A, 30% or 0.3000 in the area
column corresponds to a z-score of 0.85
c. So 60% of the cases falls between -0.85
and +0.85. Convert ±0.85 to a raw
score by transforming the formula for z-
score into a raw score.

50.  Therefore the middle 60% of cases falls
between limits of 26.66 and 33.34
30%30%
-.85 0 +.85

51. 6. What is the minimum score a pupil
should get to belong to the upper 10% of
the group?
a. 10% is at the end of the right side of the
curve, So find 40% of the scores from
the mean.
b. From Table A, column for area. There is
no 40% or 0.4000 but the value nearest
to it is 0.3997
c. 0.3997 corresponds to a z-score of 1.28
d. Convert z= 1.28 to a raw score.

52. x = zs +
= (1.28) (4) +30
= 5.12 + 30
= 35.12
So, the minimum score is 35.
𝑥
40%
10%
0 1.28𝛿

53. 7. What are the two extreme scores,
outside of which only 5% of the group can
be expected to fall?
a. Two extreme score suggests high and
low scores. Hence 5% refers to top 2.5%
and bottom 2.5%
b. 2.5% or 0.025 leaves 47.5% or 0.0475
from the mean.
c. 47.5% or 0.475 in Table A corresponds
to +1.96 above the mean and -1.96 below
the mean.

54. d. Convert ±1.96 to raw score
X = zs + x
= (±1.96)(4)+ 30
= ±7.84 +30
= 22.16 and 37.84
e. Therefore, 2.5% of the cases is expected
to fall above 37.84 or score of 38 and 2.5%
can be expected to fall below 22. (The two
extreme scores are 38 and 22).

55. 47.5% 47.5%
2.5%
2.5%
-1.96𝛿 0 + 𝟏. 𝟗𝟔𝛿

56. Exercise 9.1
Areas Under the Normal Curve Distribution
A. Find the proportion of area under the
normal curve.
1. Between the mean and z= 135
2. To the right of z= 2.54
3. To the left of z= 1.32
4. Between z= -1.35 and z=1.85
5. To the right z=1.61

57. 6. Between z= -2.25 and z=2.0
7. Between the mean and z= -.75
8. To the left of z= 1.76
9. To the left of 2.32
10. Between z= -.53 and z= -.75

58. Exercise 9.2
Areas Under the Normal Curve Distribution
In a class, 25% of the students are
expected to fail. Examination marks are
roughly normally distributed, with a mean
of 75 and a standard deviation of 6.
1. What mark must a student make to
pass?
2. What percent of the class is included
between marks of 78 and 80?
3. What is the probability of getting a mark
higher than 80?

59. 4. Between the mean and what mark below
it is include 30% of the class?
5. Within what 2 marks can we expect the
middle 95% of the cases to be included?
6. What 2 marks are so extreme that only
1% of the class is expected to fall beyond
them?