Chapter 7 Undecidable Reducible_Theory_of_Computation.ppt

Reducibility
Limits of Computation
Clayton Johnson
Edna Reiter

Classes:
Limits of Computation by Johnson & Reiter 2
Decidable: has deciding Turing machine
Acceptable/Recognizable: has accepting
Turing machine
Co-decidable: LC has deciding Turing Machine
Co-acceptable/Co-Recognizable: LC is
Turing acceptable

Some Familiar Languages
co-TM recognizable
TM-recognizable
TM decidable
EMPTY = { M | M is a TM with L(M)= }
ACCEPT = { M,w | M is a TM that accepts w }
ACCEPT_ε = { M | M is a TM that accepts ε}

You should be able to prove:
(1) ACCEPT is Turing-acceptable/recognizable
(2) EMPTY is co-Turing-acceptable
(co-Turing-recognizable)

A View of Languages
When thinking about a language L:
A) For every wL, will there be a proof of this?
B) For every wL, will there be a proof of this?
1) If A, then Turing Recognizable.
2) If B, then Co-Turing Recognizable.
3) If A and B, then Decidable.
4) If neither A nor B, then non-Recognizable
1-3 are usually easy. 4 is the “toughie”.

Halting Problem
Theorem : The ‘halting problem’ language
HALT = { M,w | the TM M halts on input w }
is undecidable (but of course recognizable).
Definition : The ‘halting problem’ language
Restated: Given a Machine and a string, does
the machine halt (not loop) on the string?

Halting Problem Proof 1
Theorem : The ‘halting problem’ language
is undecidable
Proof: Let G be a TM that decides HALT. The
following TM then decides ACCEPT:
Mdecide-ACCEPT 1) Run G to decide halting
2) If G rejected M,w then “reject”
3) If G accepted M,w, simulate M on w until it
halts.
4) If M has accepted, “accept”; otherwise, “reject”.”
then copy (reject/accept) output of M on w.

Classic pattern
1. Build a new Turing machine that has M,w built into it
2. Run M on w
3. If M accepts w, do something to produce YES of QUESTION
4. If M rejects w, do something to produce NO of QUESTION
5. If M loops on w, won’t ever produce a YES (or a NO)
Thus, if get a YES of QUESTION,
M must have accepted w
Otherwise
M rejected w or looped on w
QUESTION is UNDECIDABLE

Classic pattern applied to HALT
1. Start with a Turing machine M and its input w.
2. Build a new machine that first runs M on w
3. Now, we want to build a new M´ so that
M accepts w  M´ accepts w
M rejects w  M´ loops on w
M loops on w  we can’t put anything here
(and moreover, we don’t need to!).
Now,
Yes of halt M´  yes of M accept w
No of halt M´  no of M accept w
Answer yes/no to halt answers yes/no to accept

Classic pattern applied to
ACCEPTS_ε
1. Start with a Turing machine M and its input w.
2. Build a new machine that first runs M on w
3. Now, we want to build a new M´ so that
M accepts w  M´ accepts ε
M rejects w  M´ rejects ε
M loops on w  we can’t put anything here
(and moreover, we don’t need to!).
Undecidable: If a TM accepts ε
Yes of accept ε  yes of M accept w
No of accept ε  no of M accept w

Reducibility
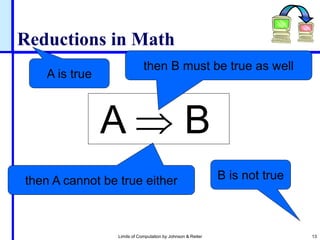
It required quite some effort to prove that ACCEPT is
not TM-decidable.
But now we can build on this result as follows:
If “L is TM-decidable” implies “ACCEPT is
decidable”, then L is not decidable.
Typical proof outline:
Let M be the TM that decides L; with this M as a
subroutine, the following TM [….] decides ACCEPT.
Conclusion: M is not TM-decidable.

Reducible P1 and P2 decision problems
´
Definition: P1 is reducible to P2 ,
P1 ≤ P2
if there is a mapping f from possible instances (yes or no) of P1
to possible instances of P2 such that:
(1) f is computable (that is, some Turing machine can compute it)
(2) if X is a yes instance of P1, then f(X) is a yes instance of P2
(3) if X is a no instance of P1, then f(X) is a no instance of P2
So:
Answering P2 (yes/no) answers P1 (yes/no)
Answering P1 may not answer P2 (why not?)

Reductions in Math
A  B
A is true
then B must be true as well
B is not true
then A cannot be true either

Reductions in CS
we can do A
we can do B as well
we cannot do B
we cannot do A either
Here B is deciding the language ACCEPT
we can do A  we can do B
B ≤ A
A is “as hard or harder than” B

Reductions in CS
ACCEPT  OUR_PROBLEM
Change YES of M_accept_w into
YES of OUR_PROBLEM
Change NO of M_accept_w into
NO of OUR_PROBLEM

Emptiness Testing (1)
Theorem EMPTY = { M | M is a TM with L(M)= }
is not decidable (but is co-TM recognizable).
Proof: What do we want?
Yes of M_accept_w  Yes of L(M)=
No of M_accept_w  No of L(M)=
This is a problem – when M loops on w
the language accepted will be empty!

Theorem EMPTY = { M | M is a TM with L(M)= }
is not decidable (but is co-TM recognizable).
Proof: What will work?
Yes of M_accept_w  No of L(M)=
No of M_accept_w  Yes of L(M)=
If we can tell the difference – we can tell
whether M accepted w!

Restated: Assume we can tell if whether or not
L(M)= -- now show we can tell if M accepts w
Or: If the complement of a language is decidable,
then so is the language
Yes of M_accept_w  L(M)≠
No of M_accept_w  L(M)=

Yes of M_accept_w  L(M)≠
No of M_accept_w  L(M)=
This is easy: construct M′:
(1) Ignore input x, run M on w
(2) If M accepts w, M′ accepts x
(3) If M rejects w, M′ rejects x
This satisfies the conditions required….

Rice’s Theorem
Rice’s Theorem: Any nontrivial property of TM
languages is undecidable.
Nontrivial: Some languages have the property,
some do not.
Note: property of languages, not of the machines
(thus, it may be decidable to answer something
such as “machine has at least 200 states”)

Proof of Rice’s Theorem (1)
We begin with a non-trivial property of TM languages
Either the empty set has this property or it doesn’t
Assume it doesn’t
Now, since this property is nontrivial, there is a
language that does have the property. Call it Lprop
Since Lprop is a TM language, is accepted by some
TM – call it Mprop

Rice proof (2)
M′:
M accepts w?
Accept strings in Lprop
Accept no strings
YES
NO
M′ on input x: (1) ignore x, run M on w
(2) if M accepts w, run Mprop on x and accept if Mprop accepts
(3) if M rejects w, M′ rejects x

Proof of Rice (3)
M′:
M accepts w?
Accept strings in Lprop
Accept no strings
L(M′) = Lprop = language with the property
OR
L(M′) = ∅ = language not have the property

Consequences of Rice’s Thm.
Almost any language property of Turing machines
is undecidable:
RegularTM = { M | L(M) is a regular language }
FiniteTM = { M | L(M) is a finite language }
CFGTM = { M | L(M) is a CFG language }

Halting Problem (again!)
Problem: write a C++ program ILDP that takes a
C++ program P with input I as input, and writes
“loops” or “terminates” depending on what P does
CLAIM: ILDP cannot exist
PROOF: contradiction
ILDP
P, I
Loop
Terminate

Halting Problem (2)
(1)Change ILDP to ILDP′ which asks if P loops or
halts when P is run on P
(2)Now change the “yes, terminates” state into an
infinite loop. Call this ILDP′′
(3) Send ILDP′′ to ILDP′′
ILDP′′
ILDP′′
Loop
Terminate
Go right

Halting Problem (3)
(1) If ILDP′ stops and announces “loop” then it
has gone into a non-terminating loop. But
it stopped!
(2) If IDLP′′ on itself announces that it terminates,
then it goes into a infinite loop marching right
(3) So IDLP′′ (and IDLP) cannot exist
ILDP′′
ILDP′′
Loop
Terminate Go right

Computation Histories
An accepting computation history for a TM M on a
string w consists of a sequence of configurations
C1,C2,…,Ck such that the following properties hold:
1. C1 is the start configuration of M on w
2. Each Cj+1 follows properly from Cj
3. Ck is an accepting configuration
Observation: Stating “M,wACCEPT” is
Equivalent to stating “There is no accepting
computation history C1,…,Ck for M on w”.

FACT: For many machines, there are only a finite
number of possible configurations.
If you run such a machine long enough, it must
repeat (re-enter) one of its configurations
Obviously, a deterministic machine that repeats
a previous configuration is in an infinite loop.

FACT: For many machines, there are only a finite
number of possible configurations. BUT NOT
TURING MACHINES!!!
Which category does your PC belong to? Your
supercomputer? Depends on point of view…
Any machine with a finite memory however does
only have a finite number of configurations.

If we had more time…
The Post Correspondence Problem (PCP)
Given Σ, and n pairs (ai, bi), i=1,n, with ai and
bi strings from Σ+ (so no string can be
empty), is there a sequence i1, i2, … ik of
integers, not necessarily distinct, 1 ≤ i,j ≤ n,
so that :
ai1 ai2 ai3 … aik = bi1 bi2… … bik

If we had more time…
Corollary to PCP
The following is undecidable: Given a
grammar G, is it ambiguous (does some
string have at least two parse trees)?

Chapter 7 Undecidable Reducible_Theory_of_Computation.ppt

More Related Content

Similar to Chapter 7 Undecidable Reducible_Theory_of_Computation.ppt

Recently uploaded

Chapter 7 Undecidable Reducible_Theory_of_Computation.ppt