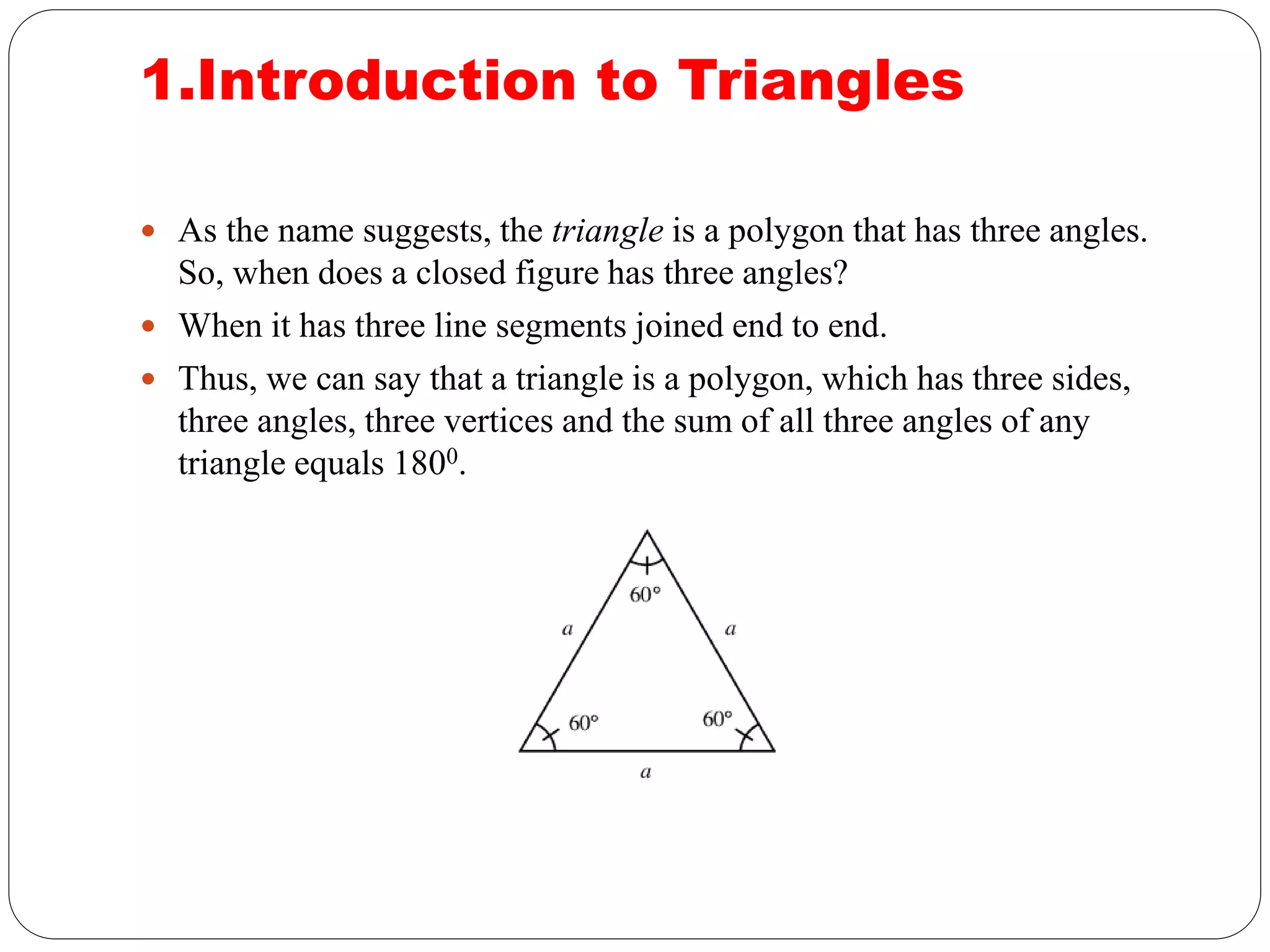
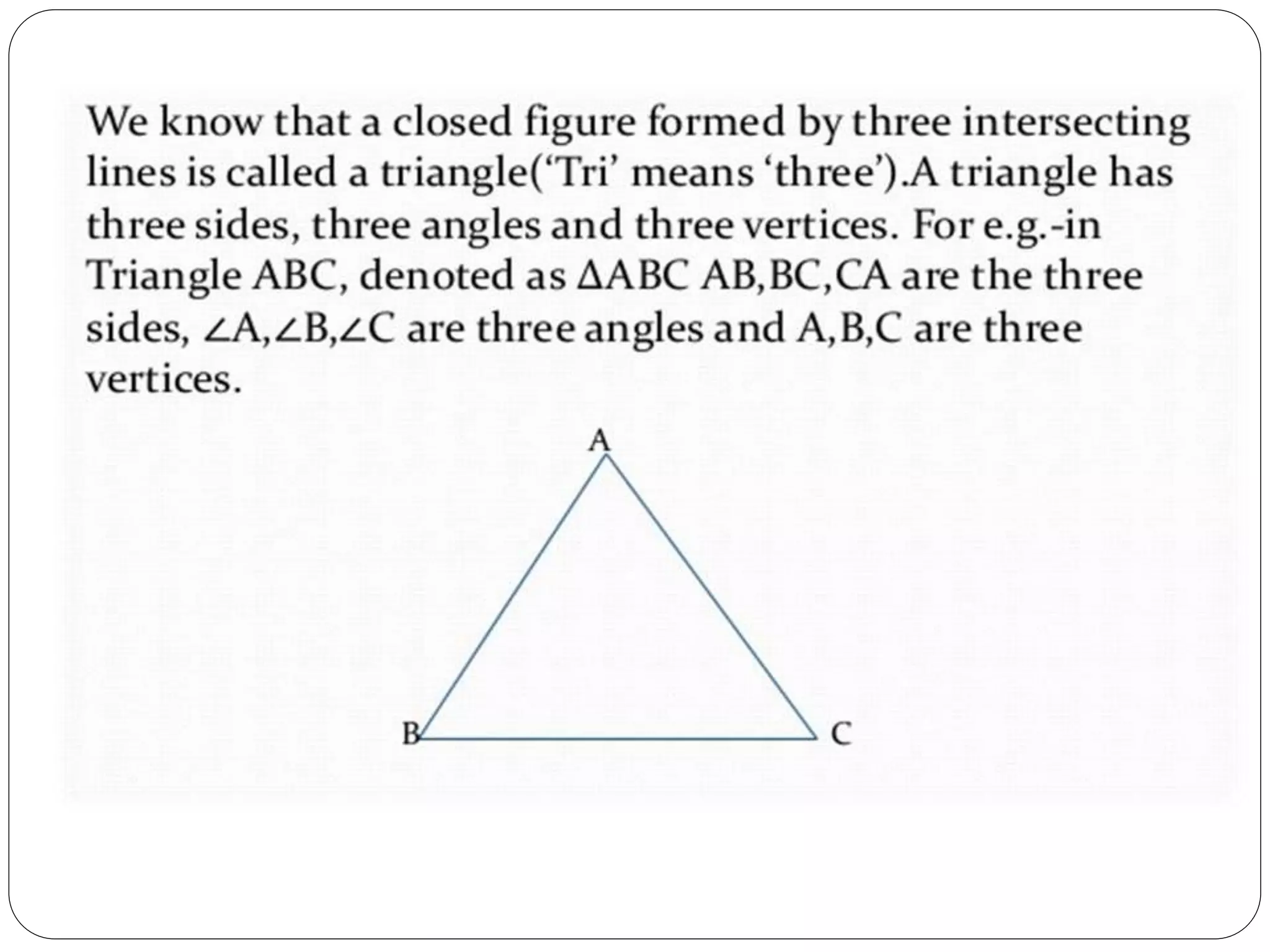
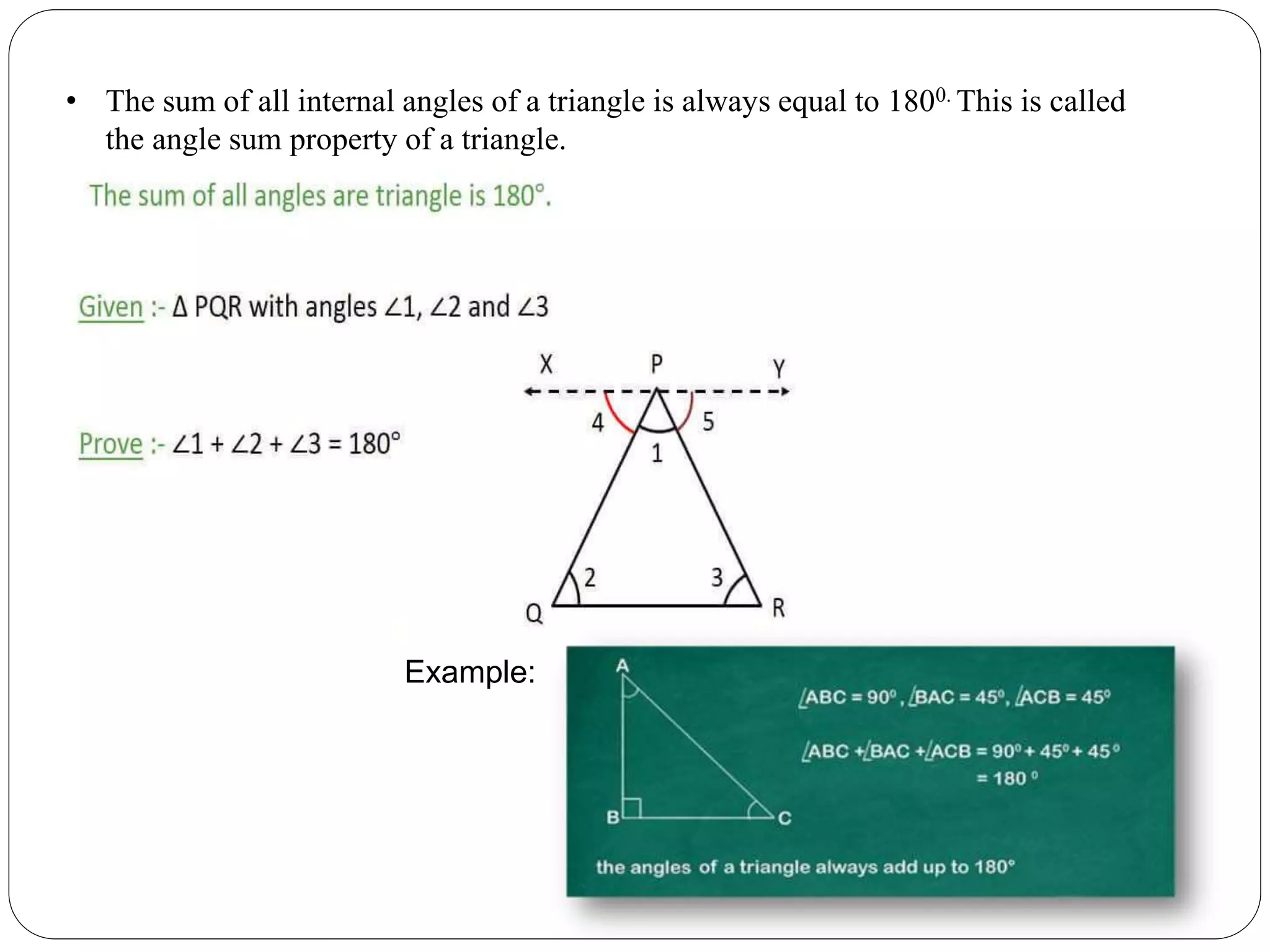
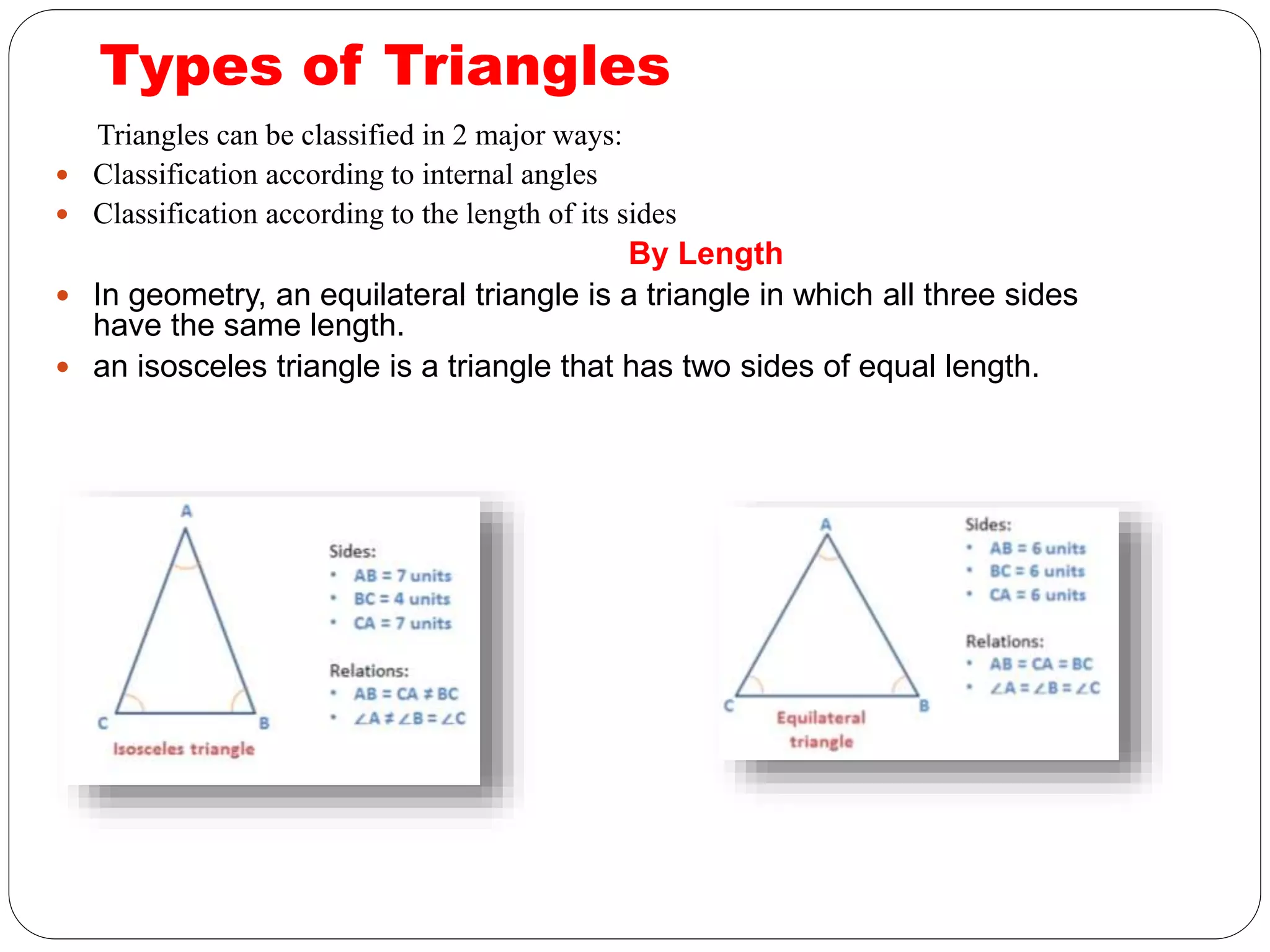
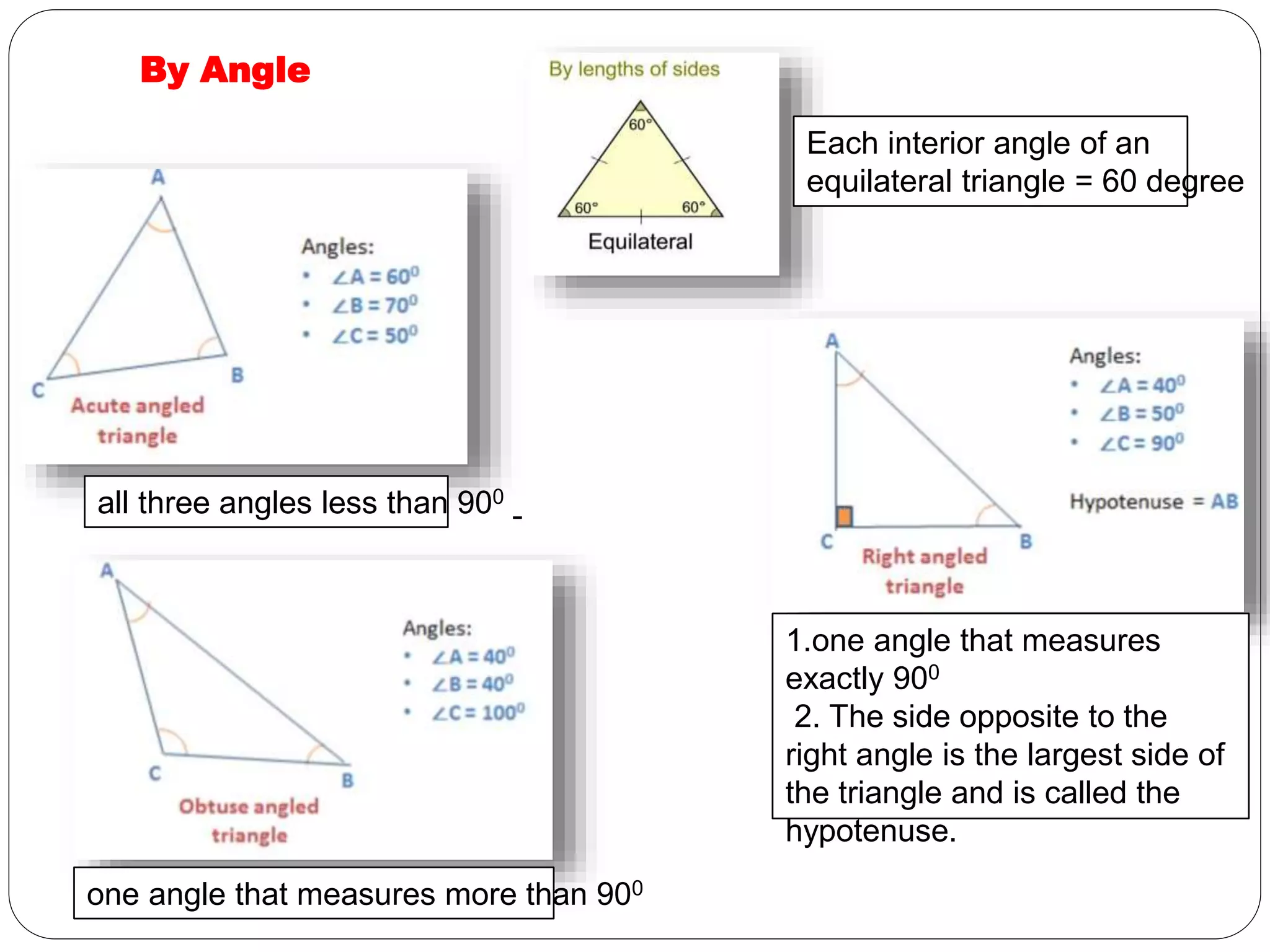
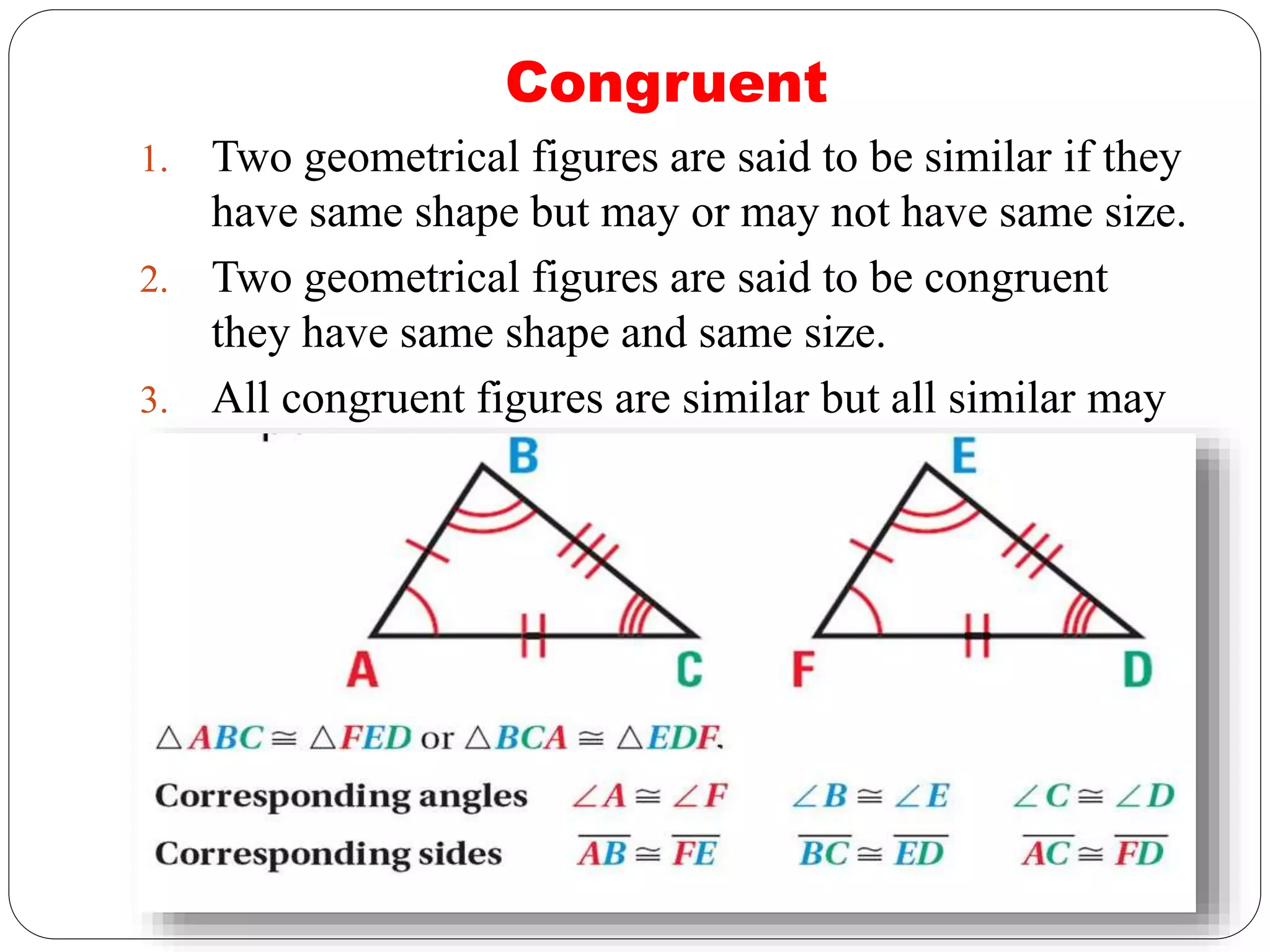
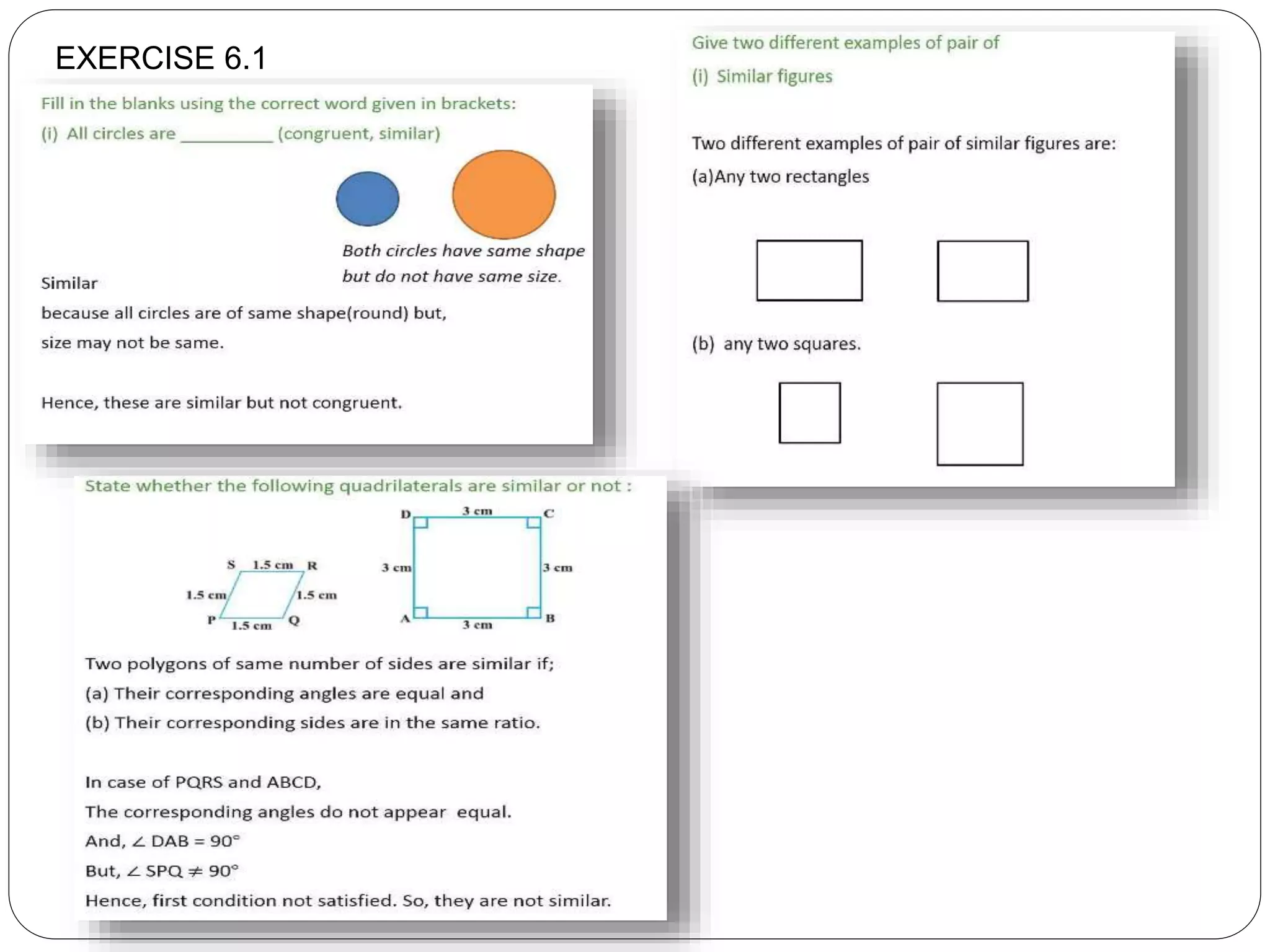
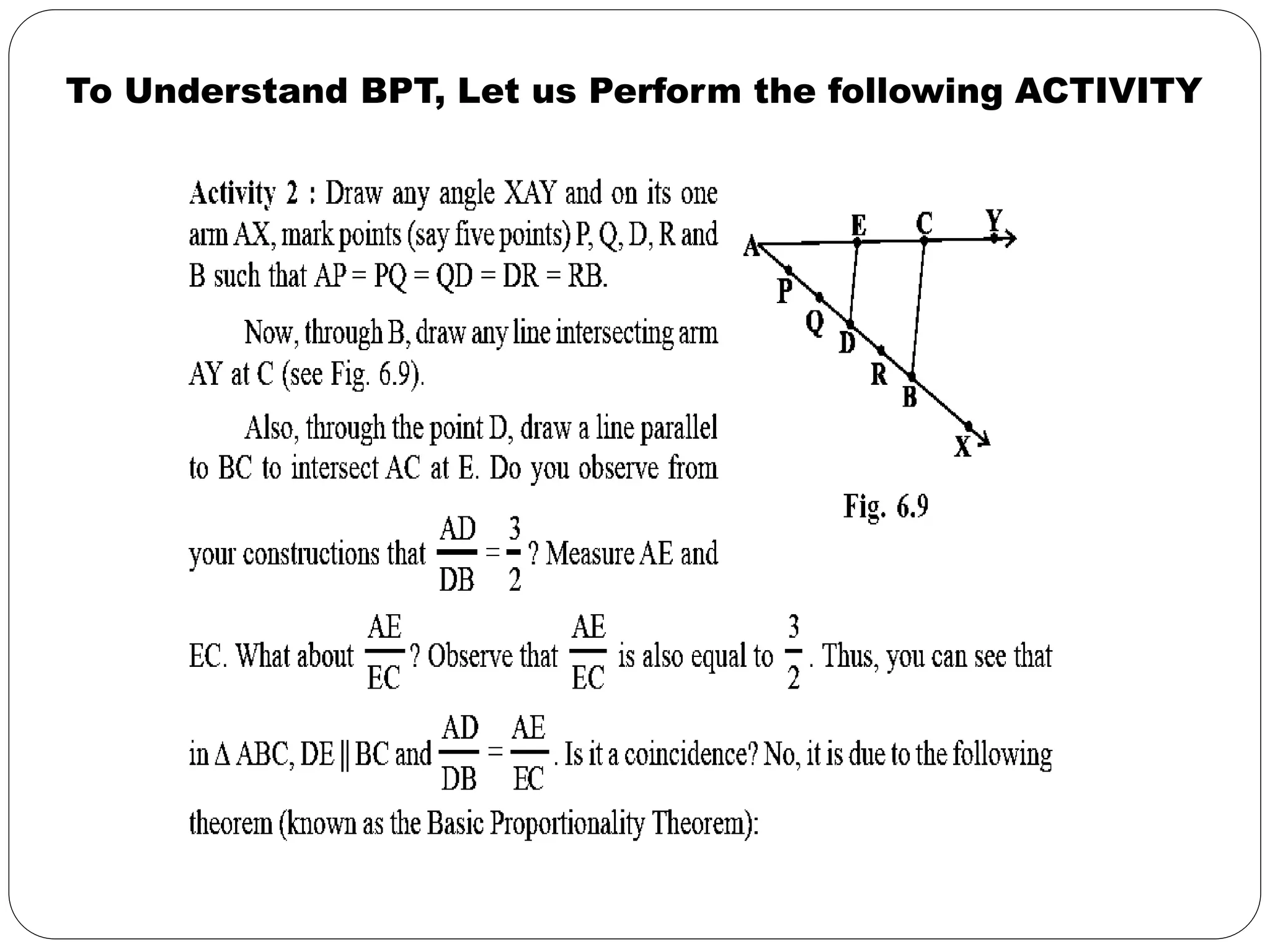
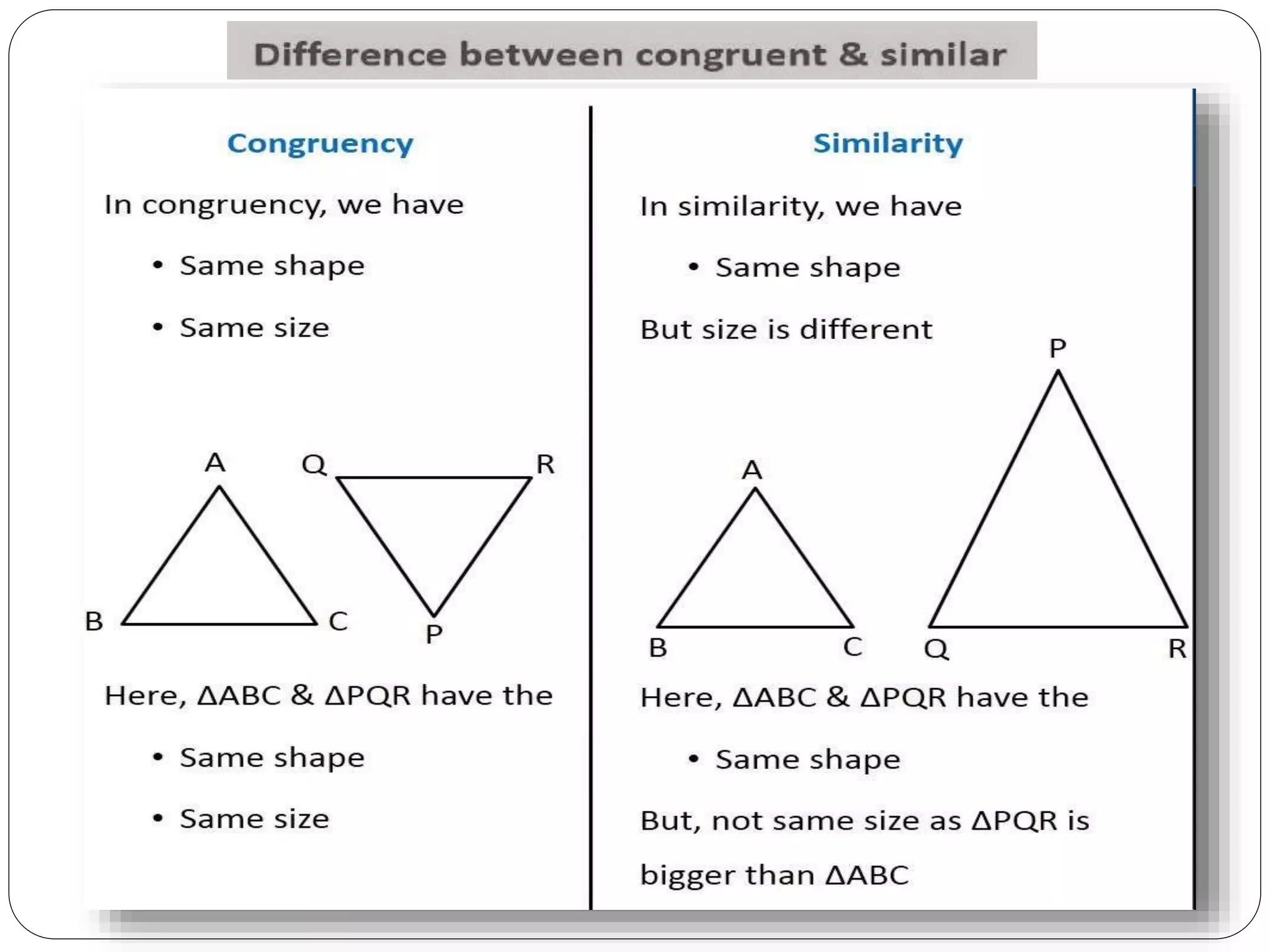
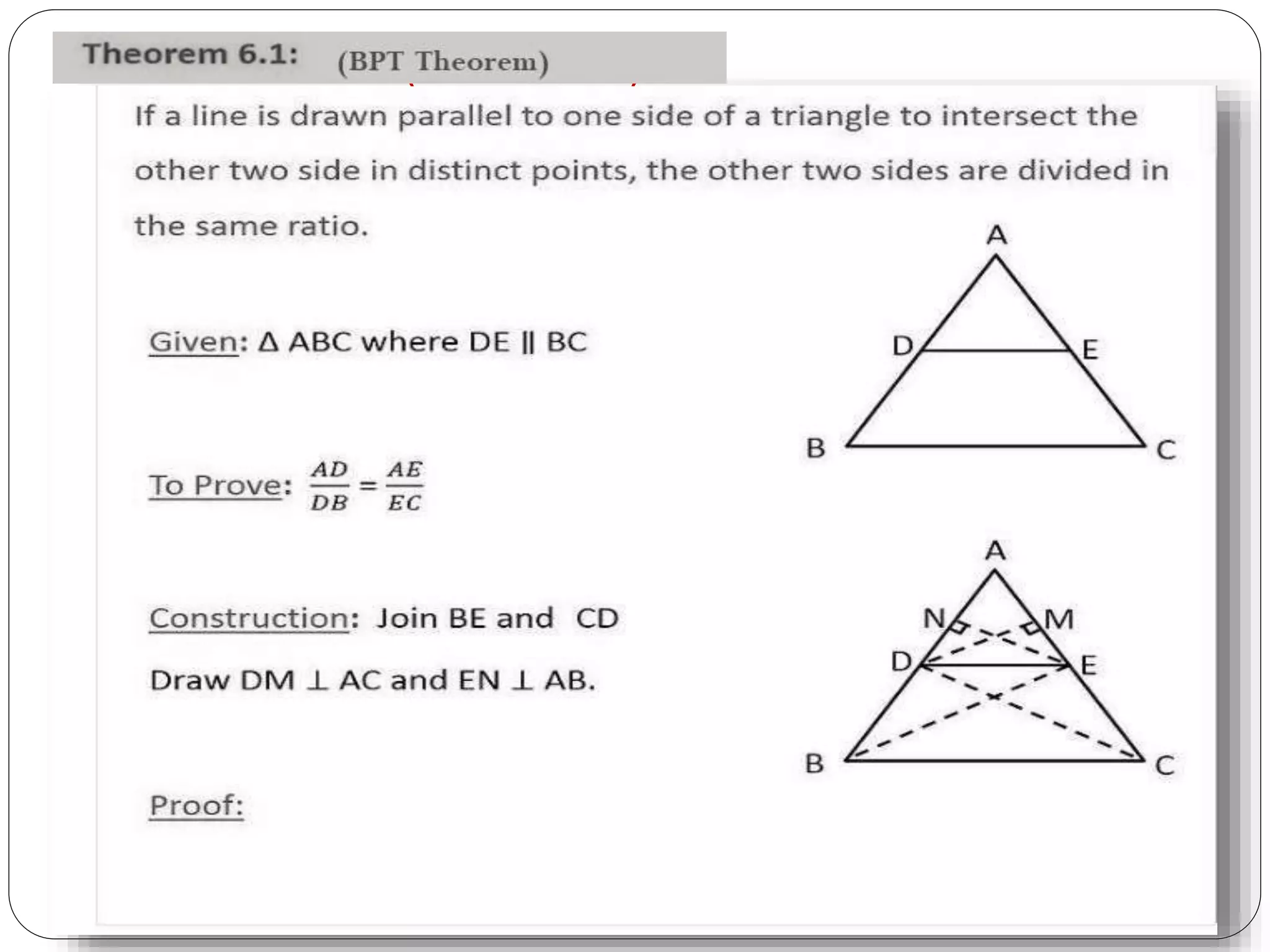
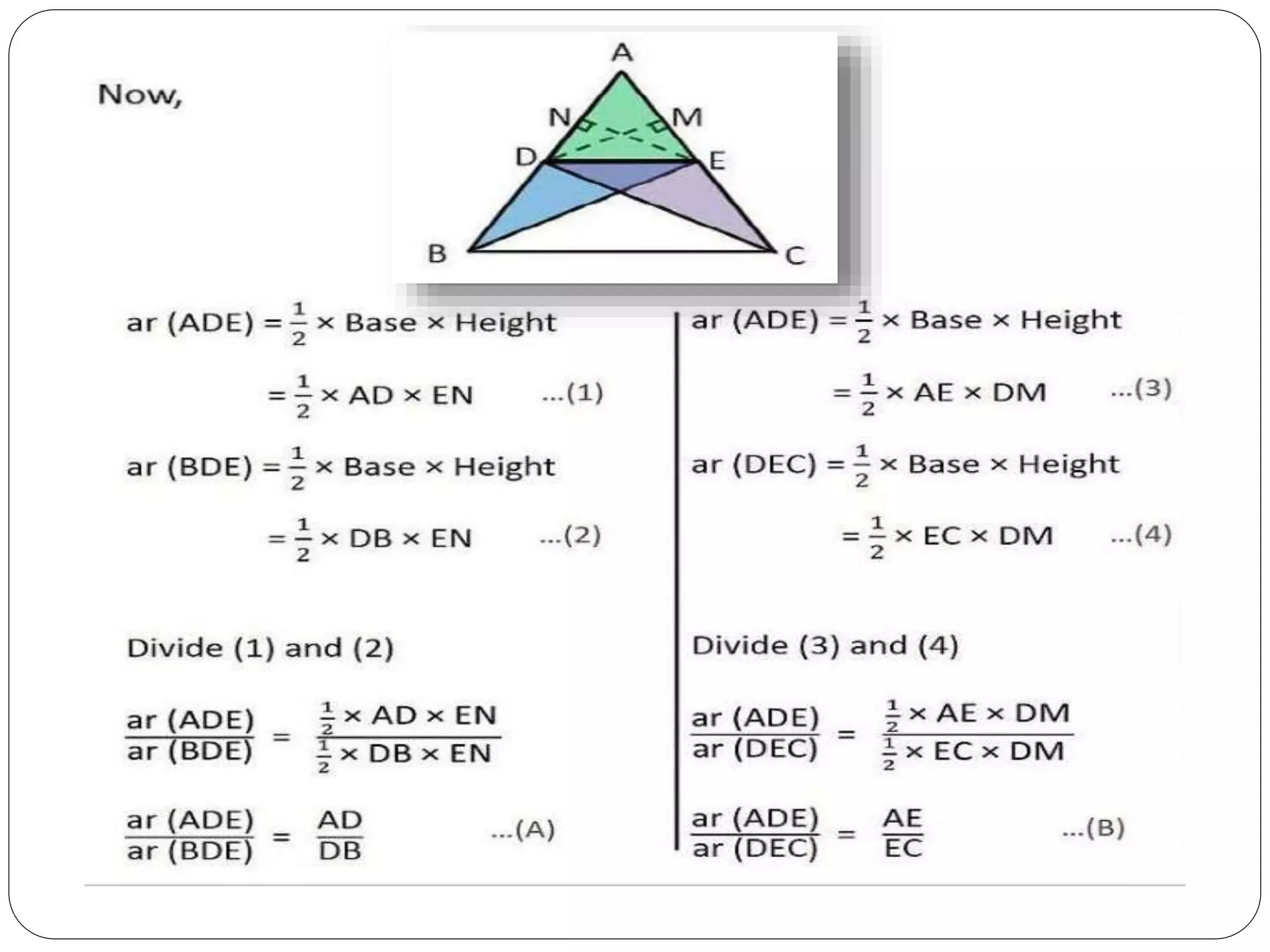
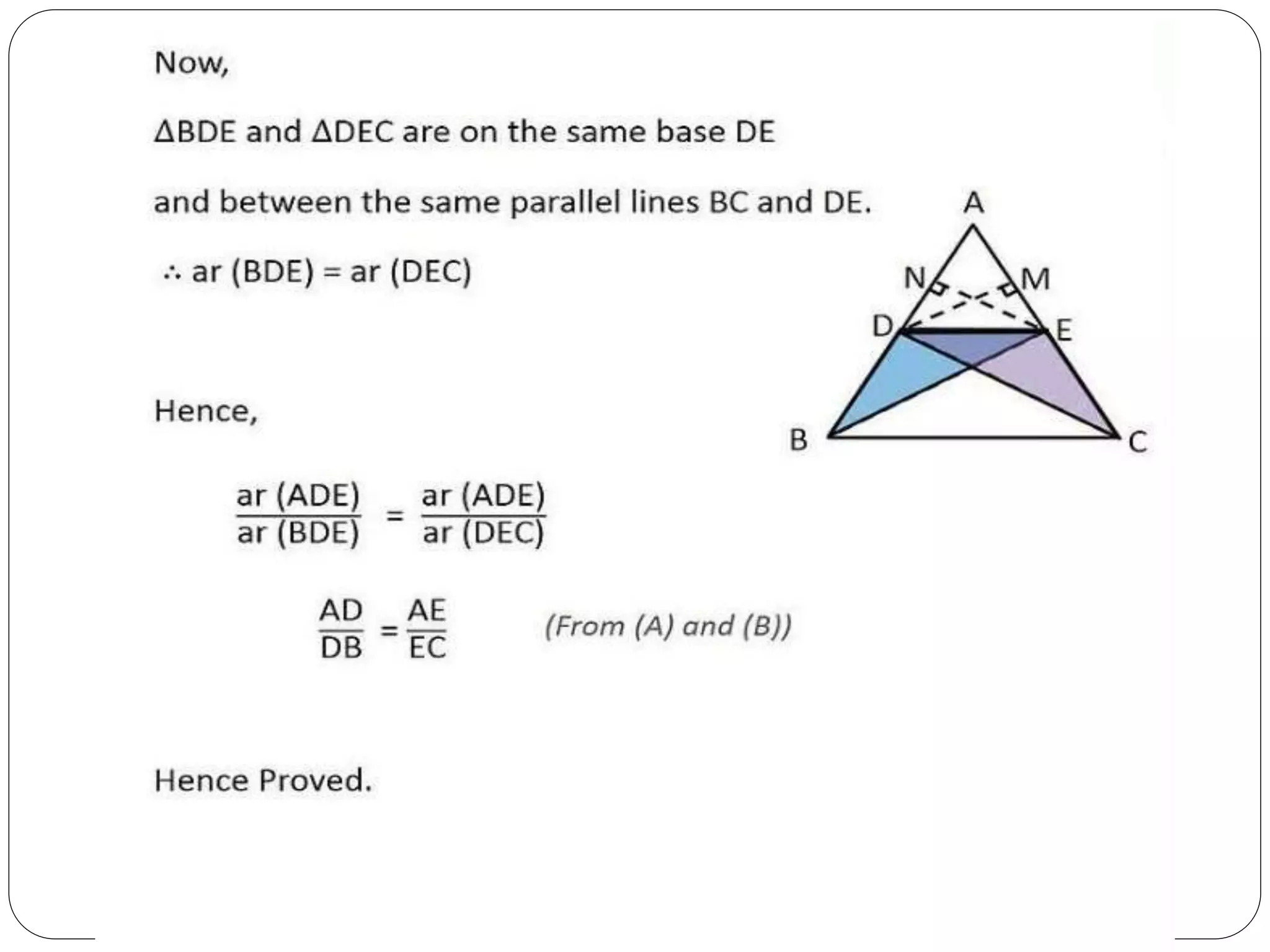
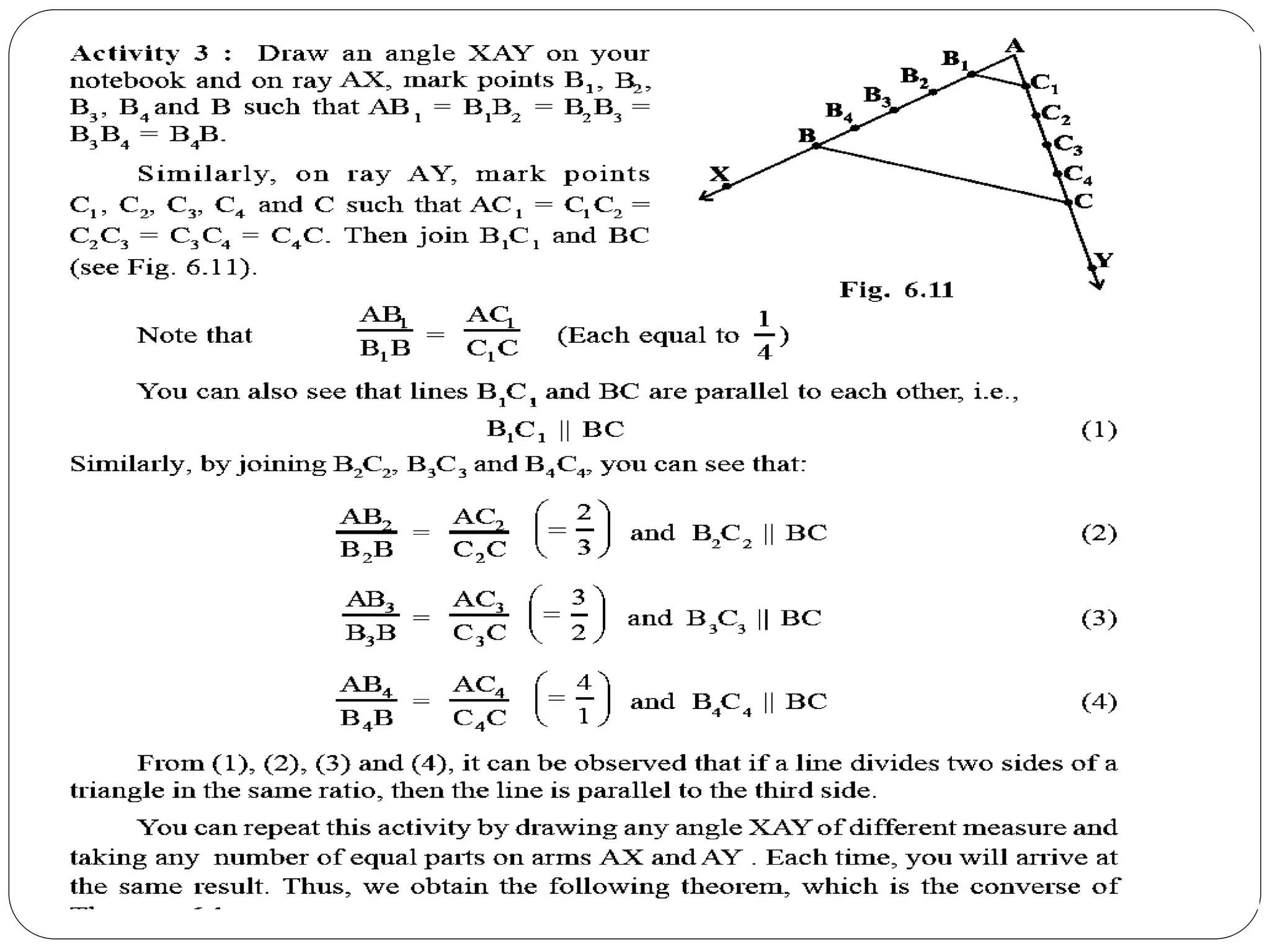
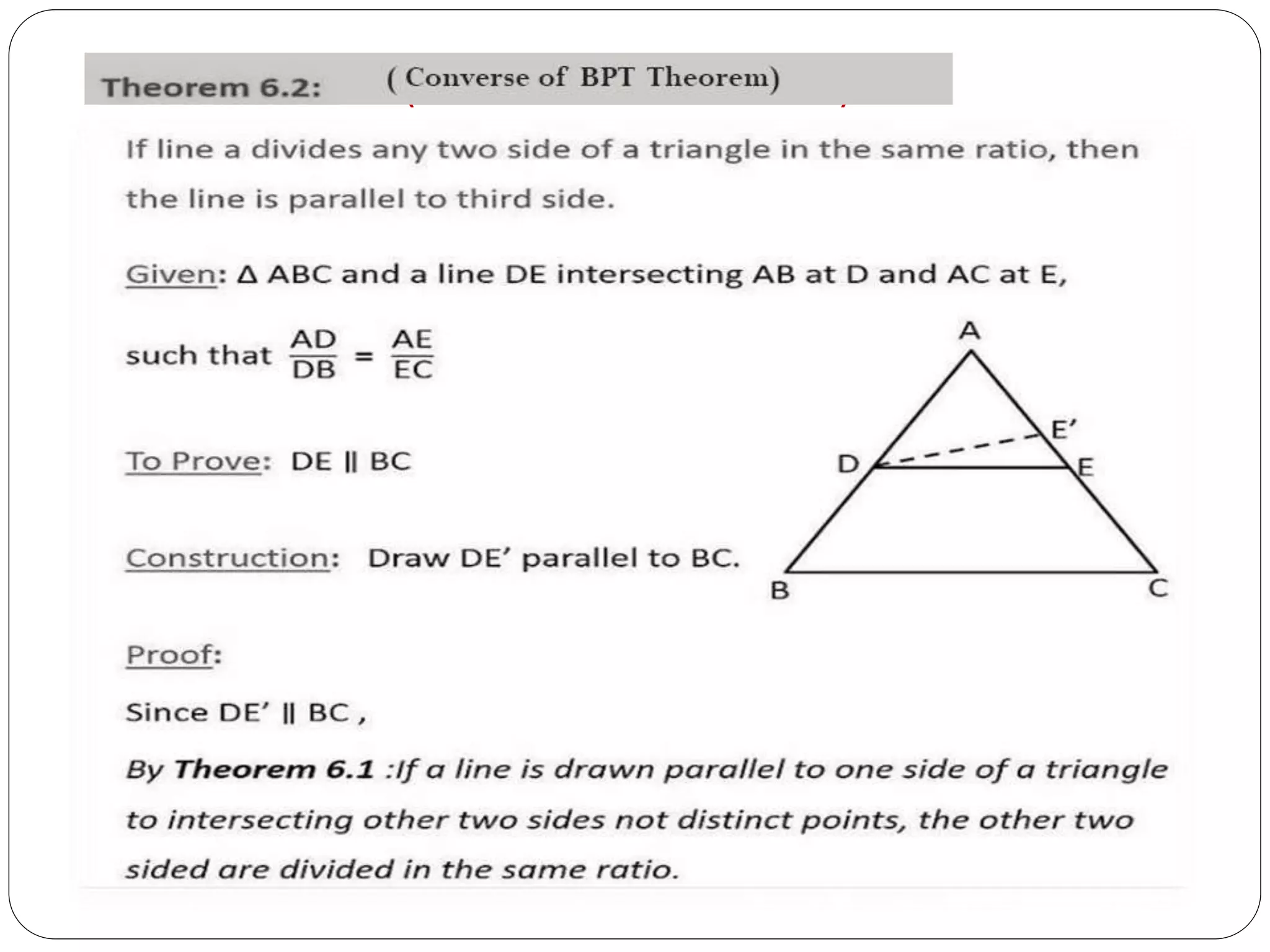
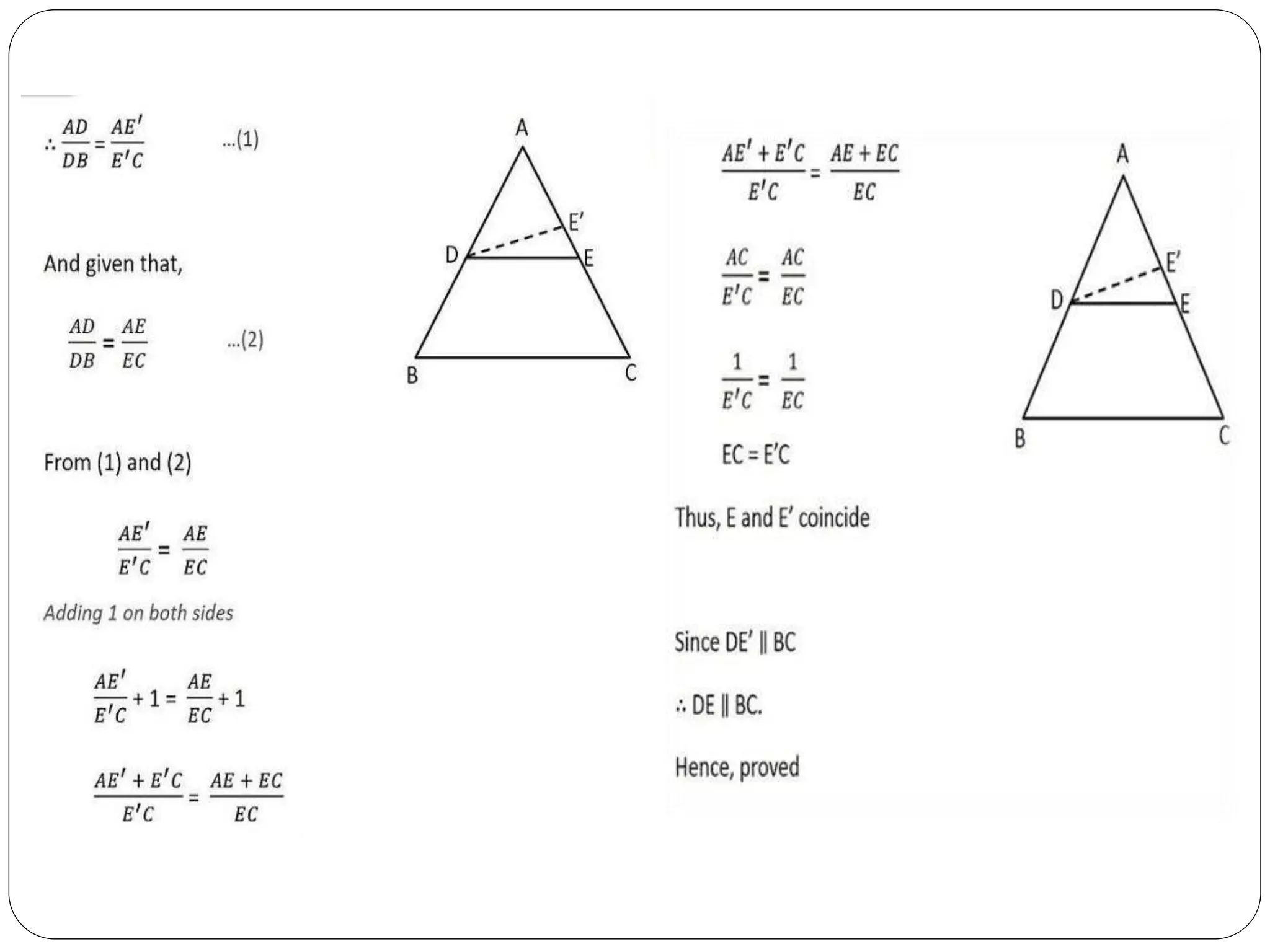
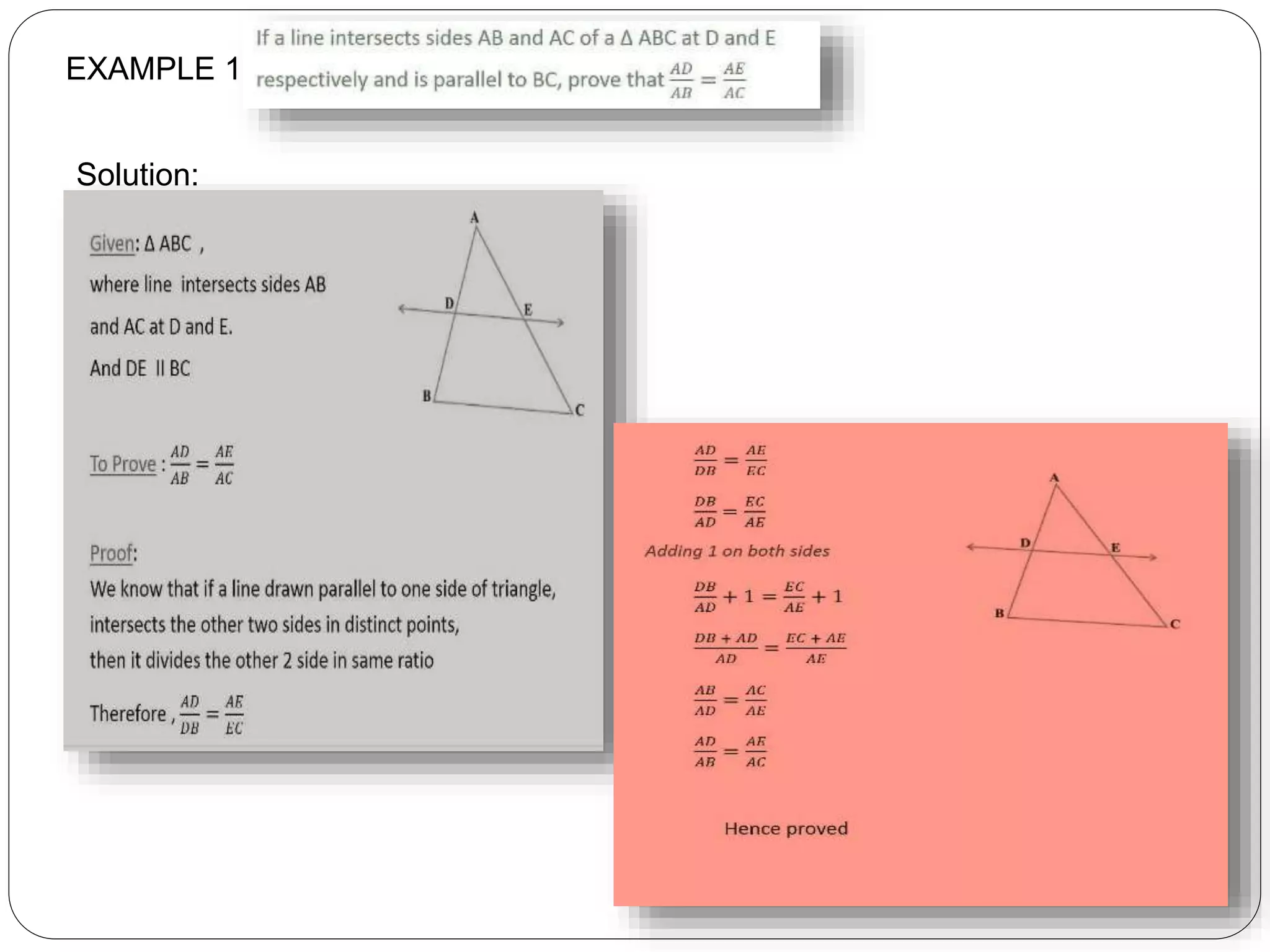
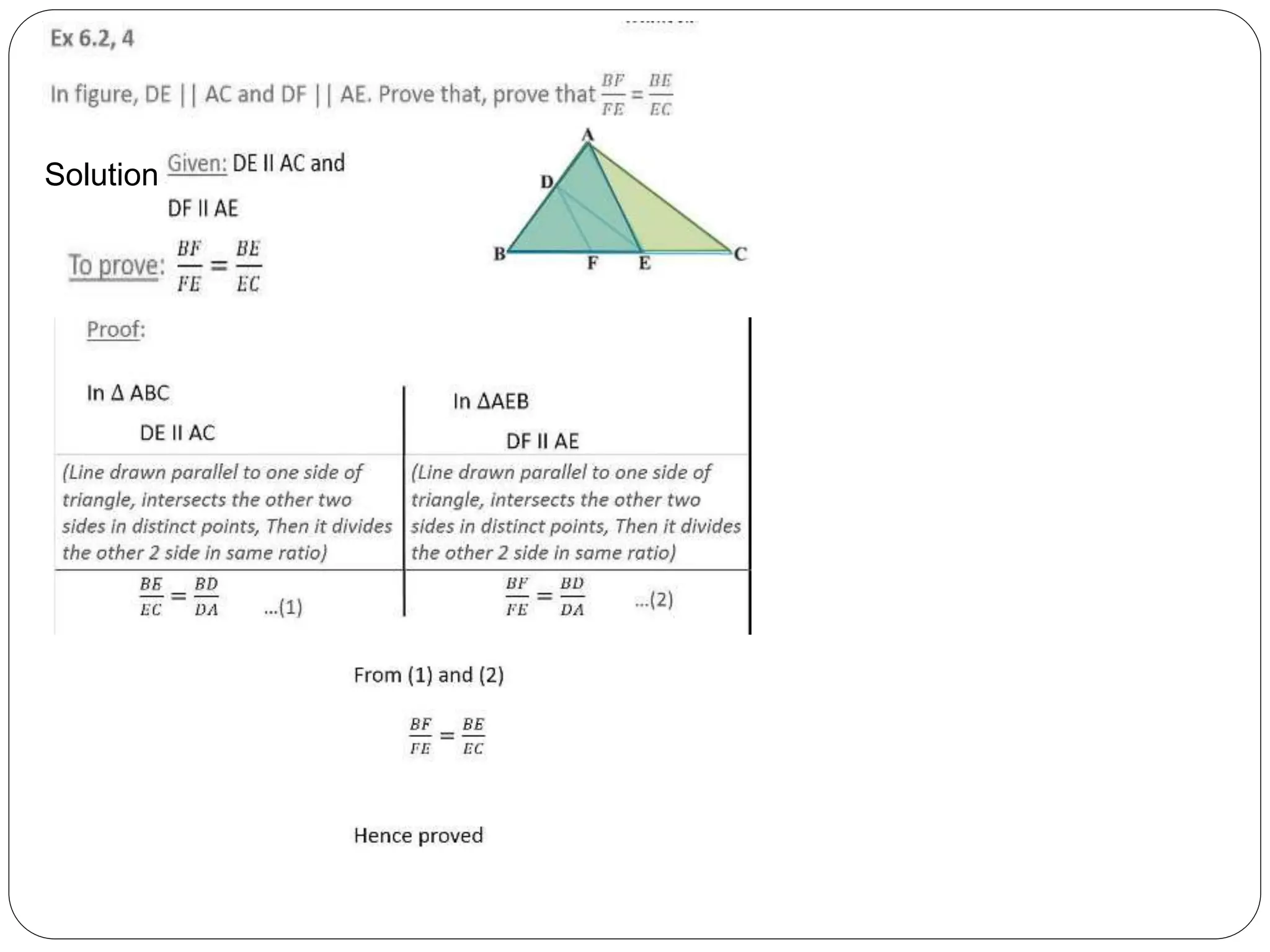
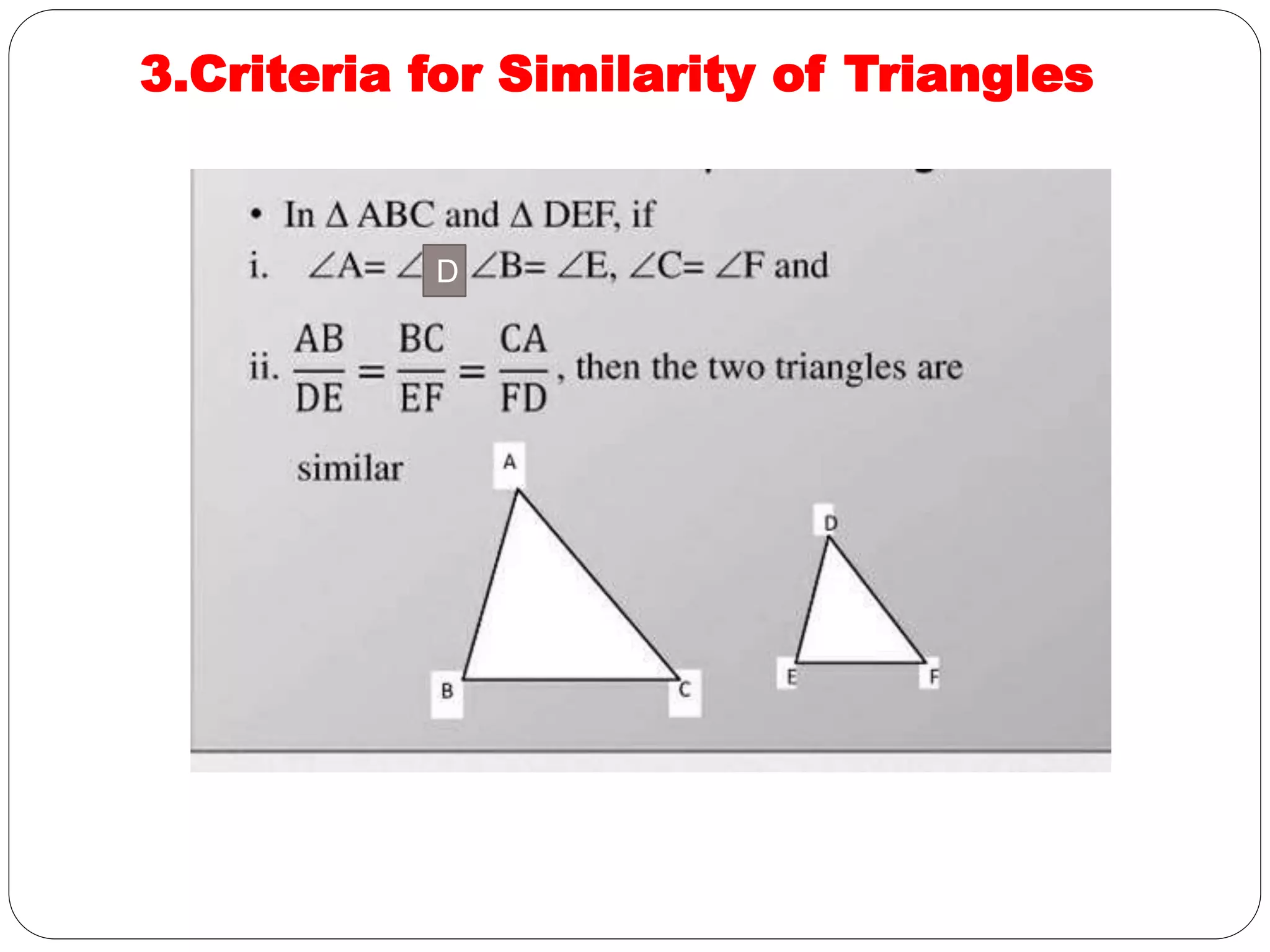
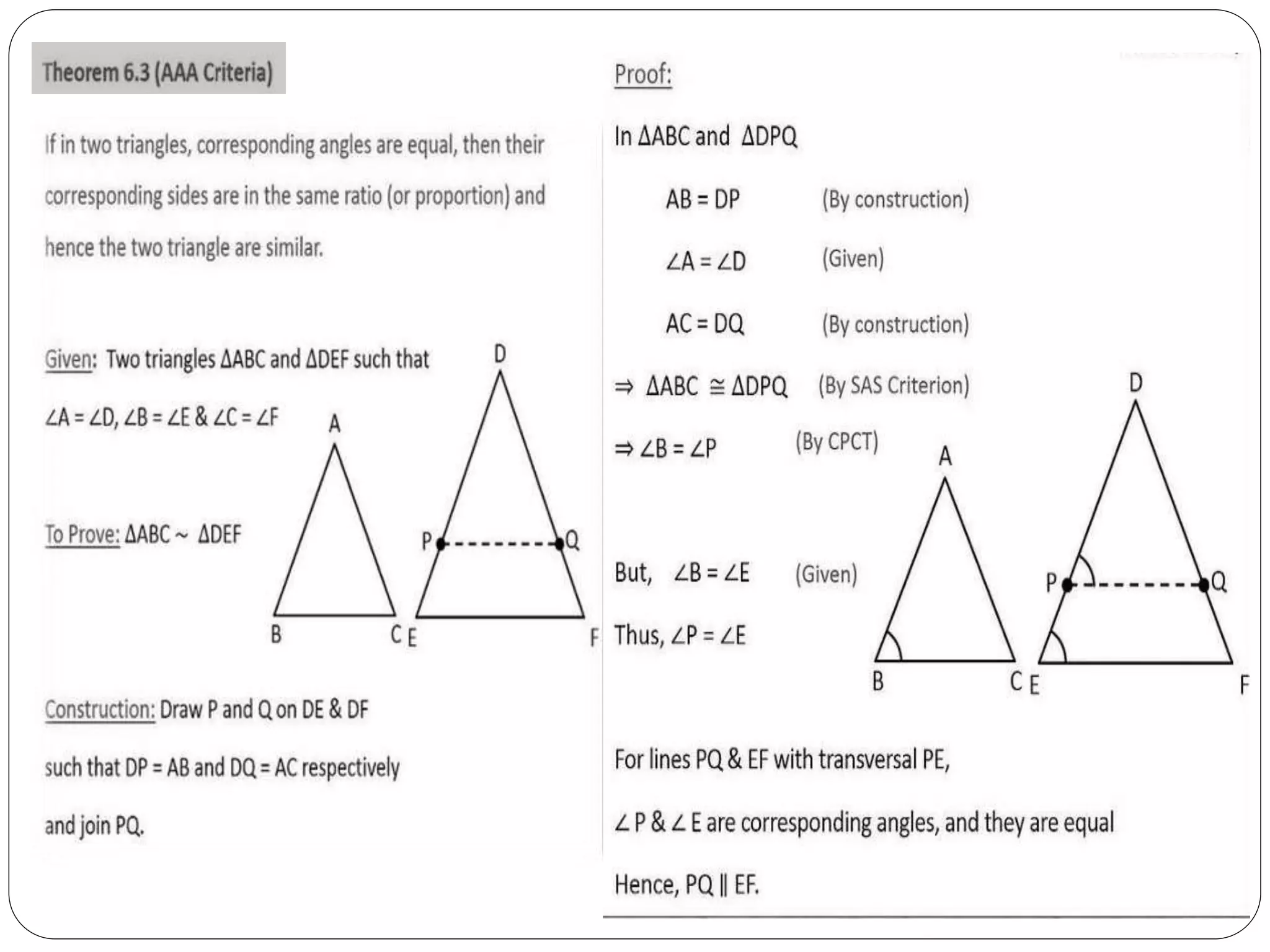
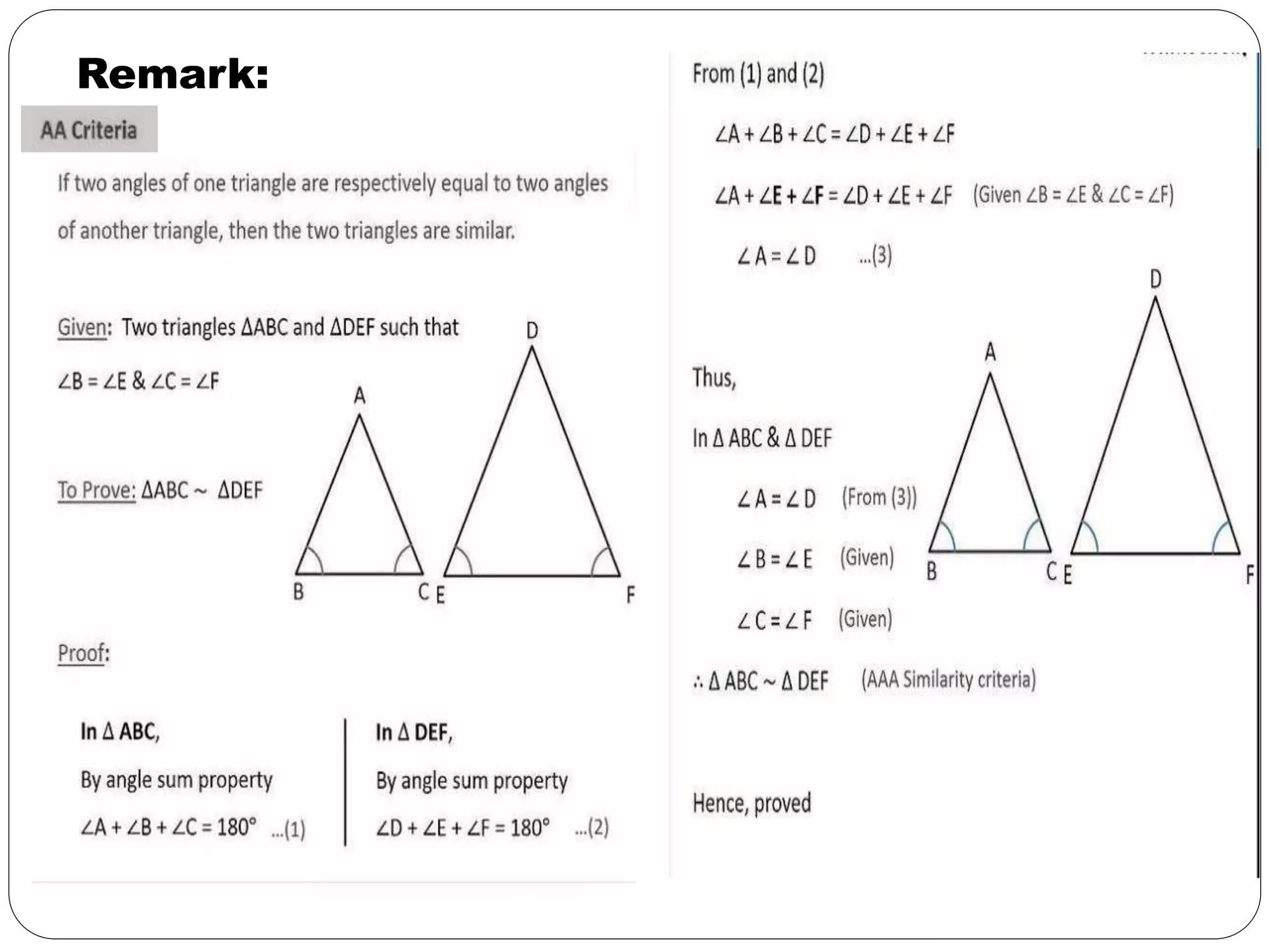
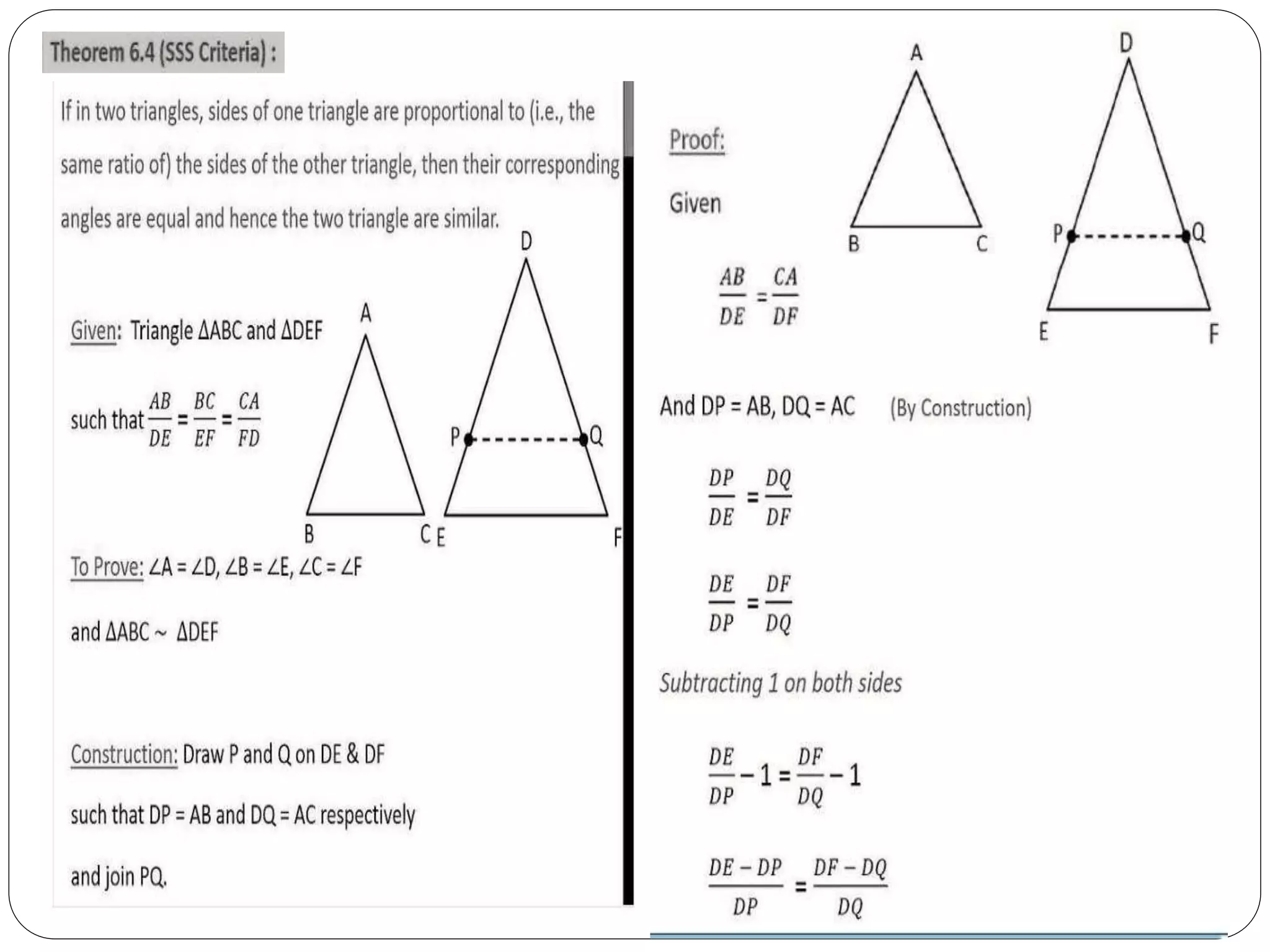
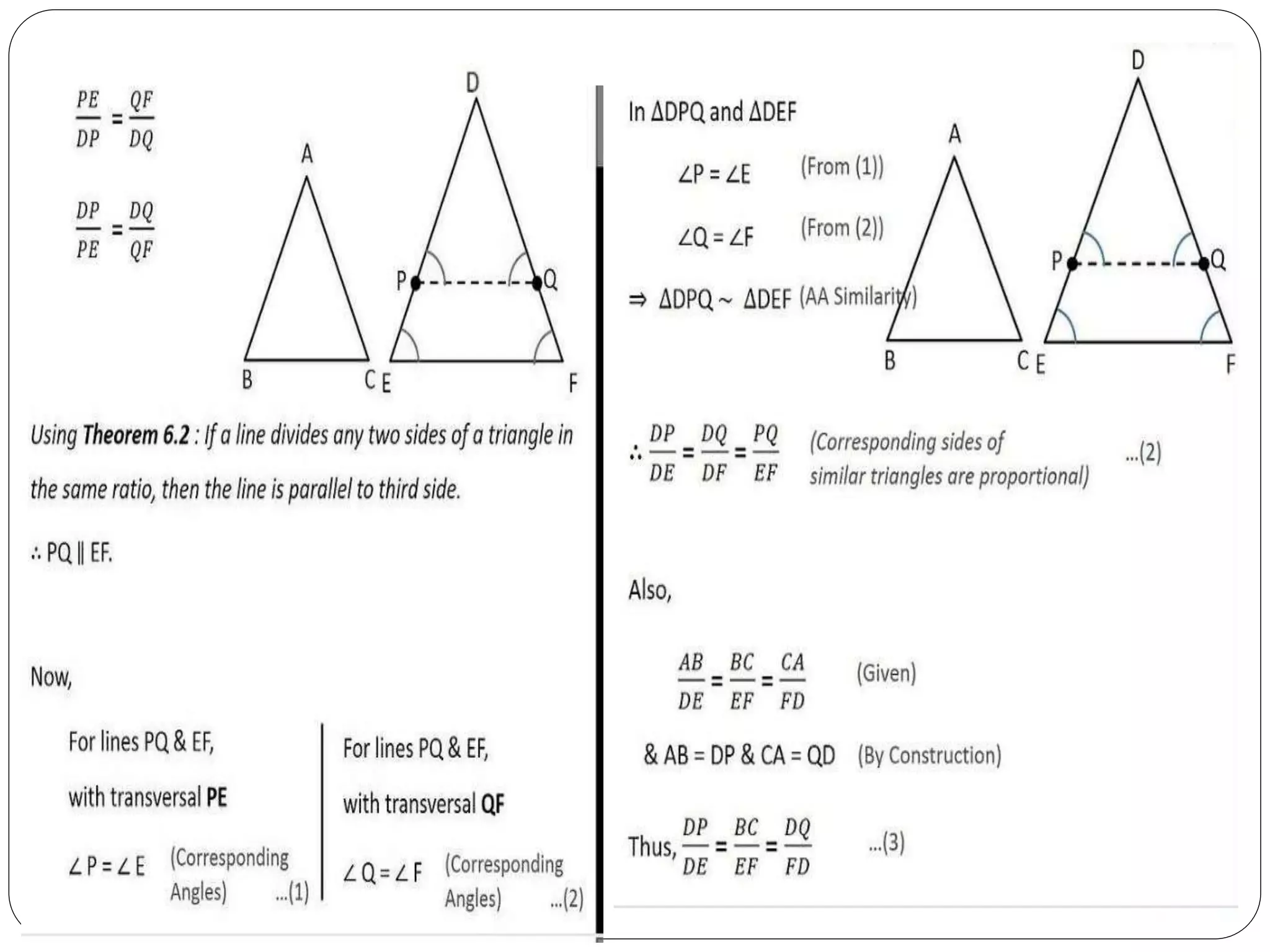
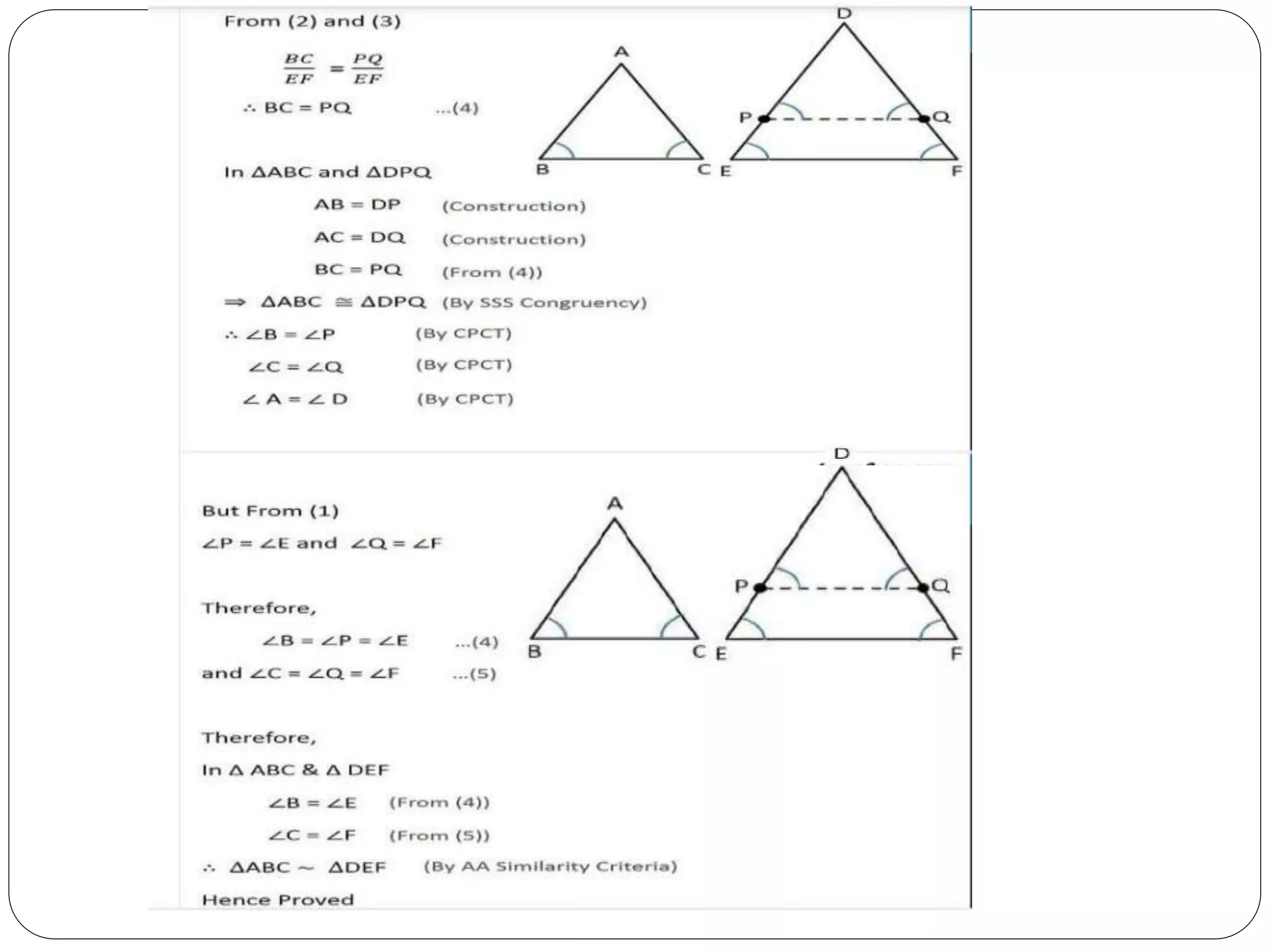
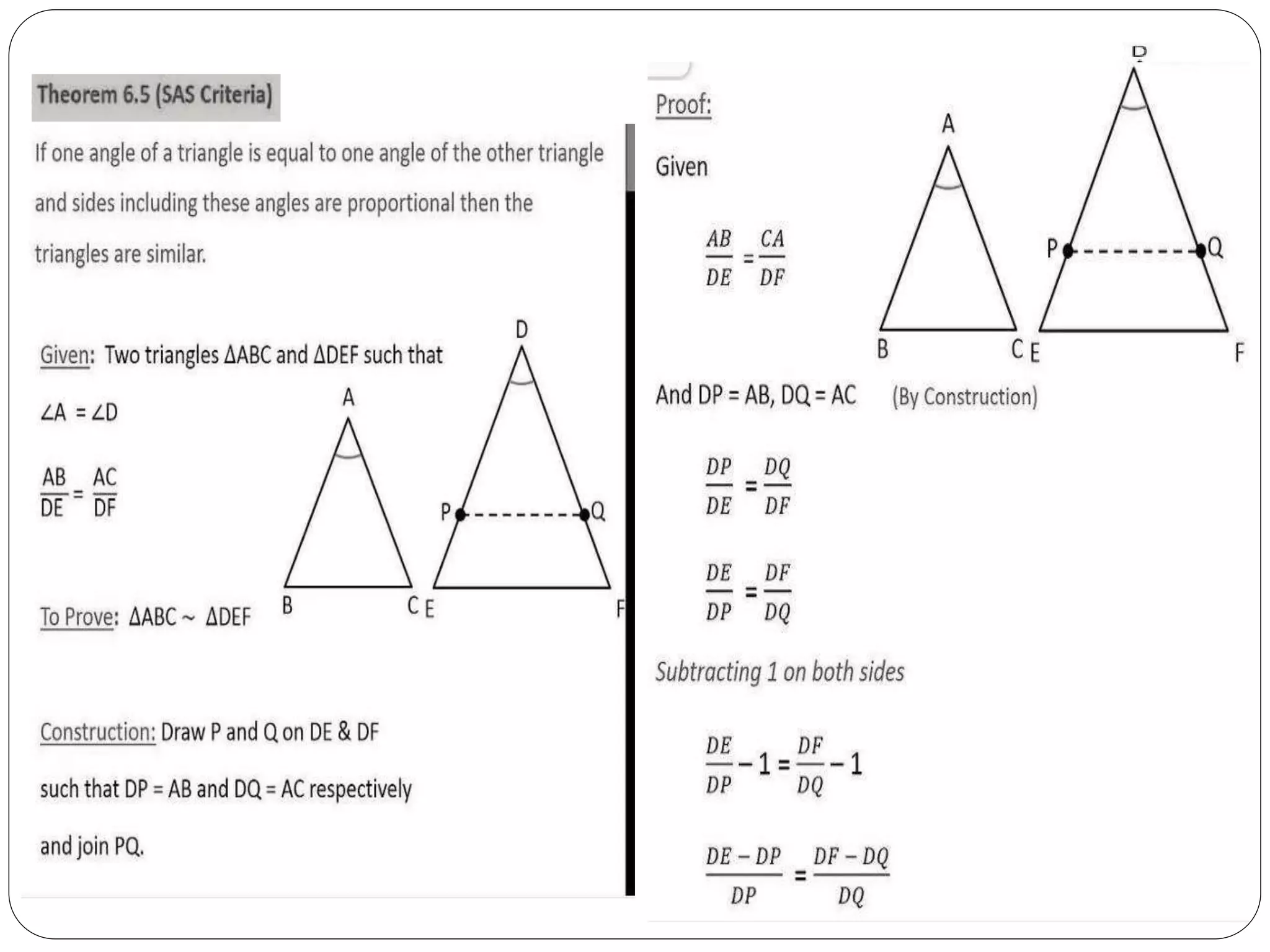
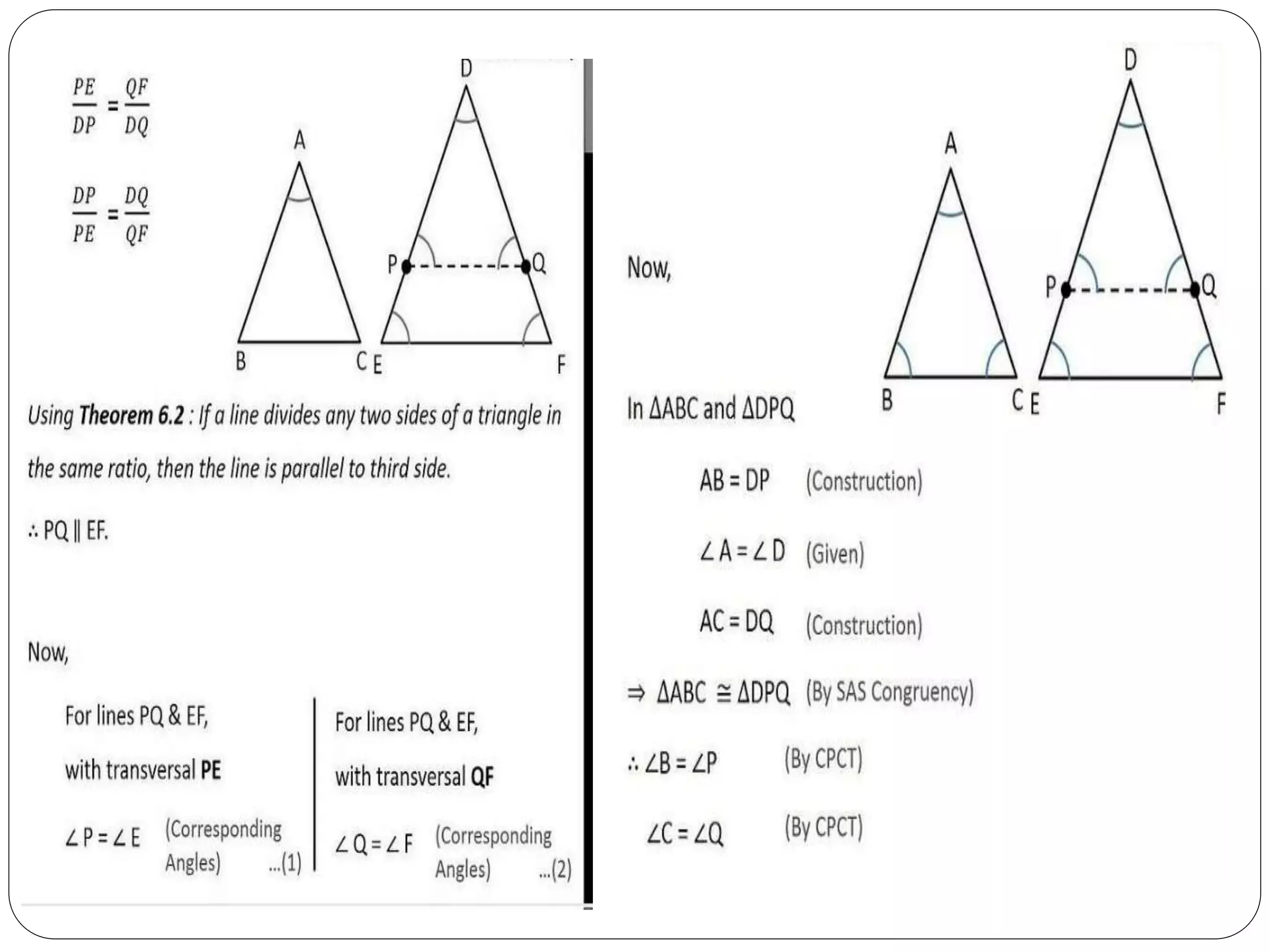
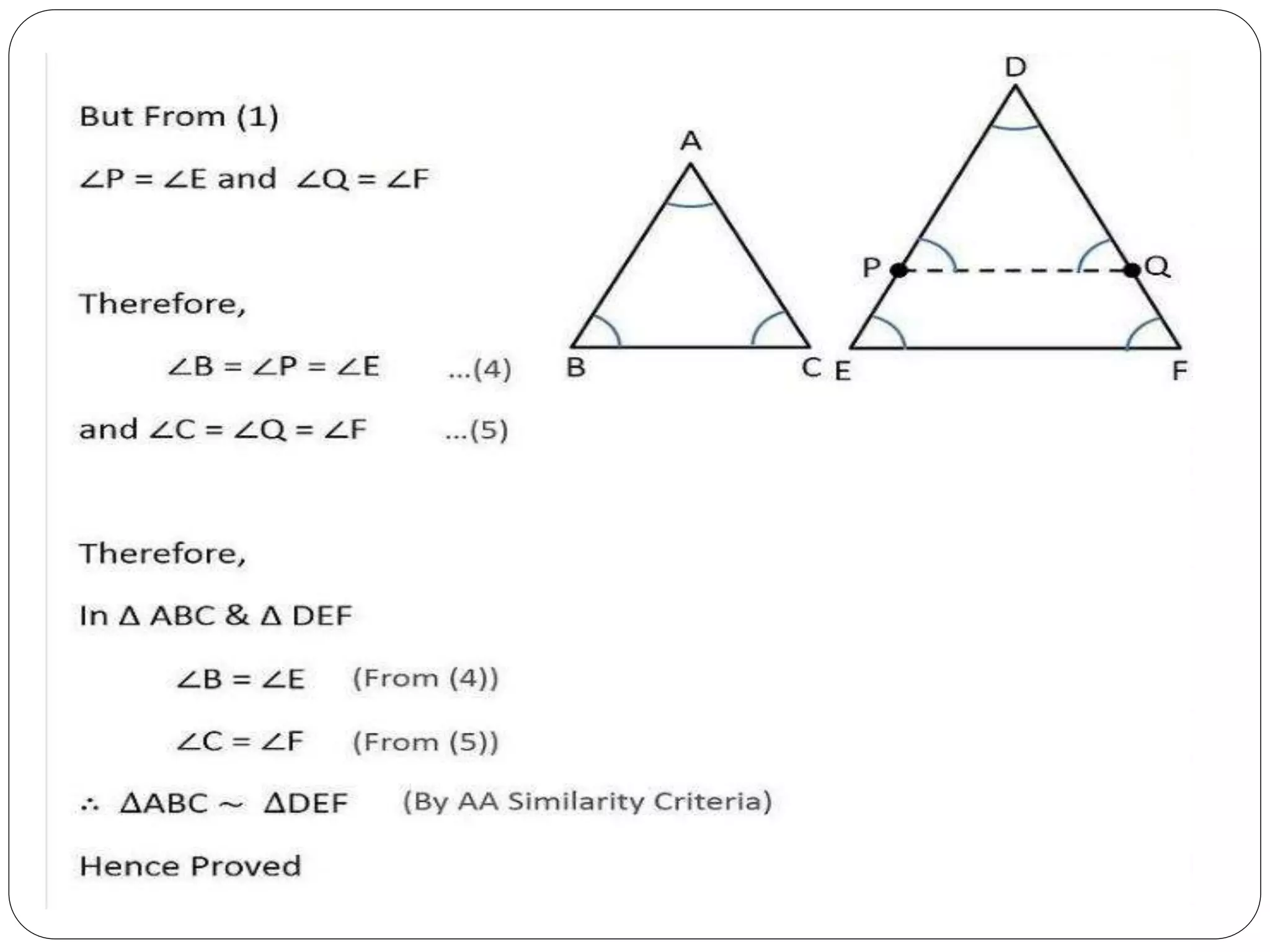
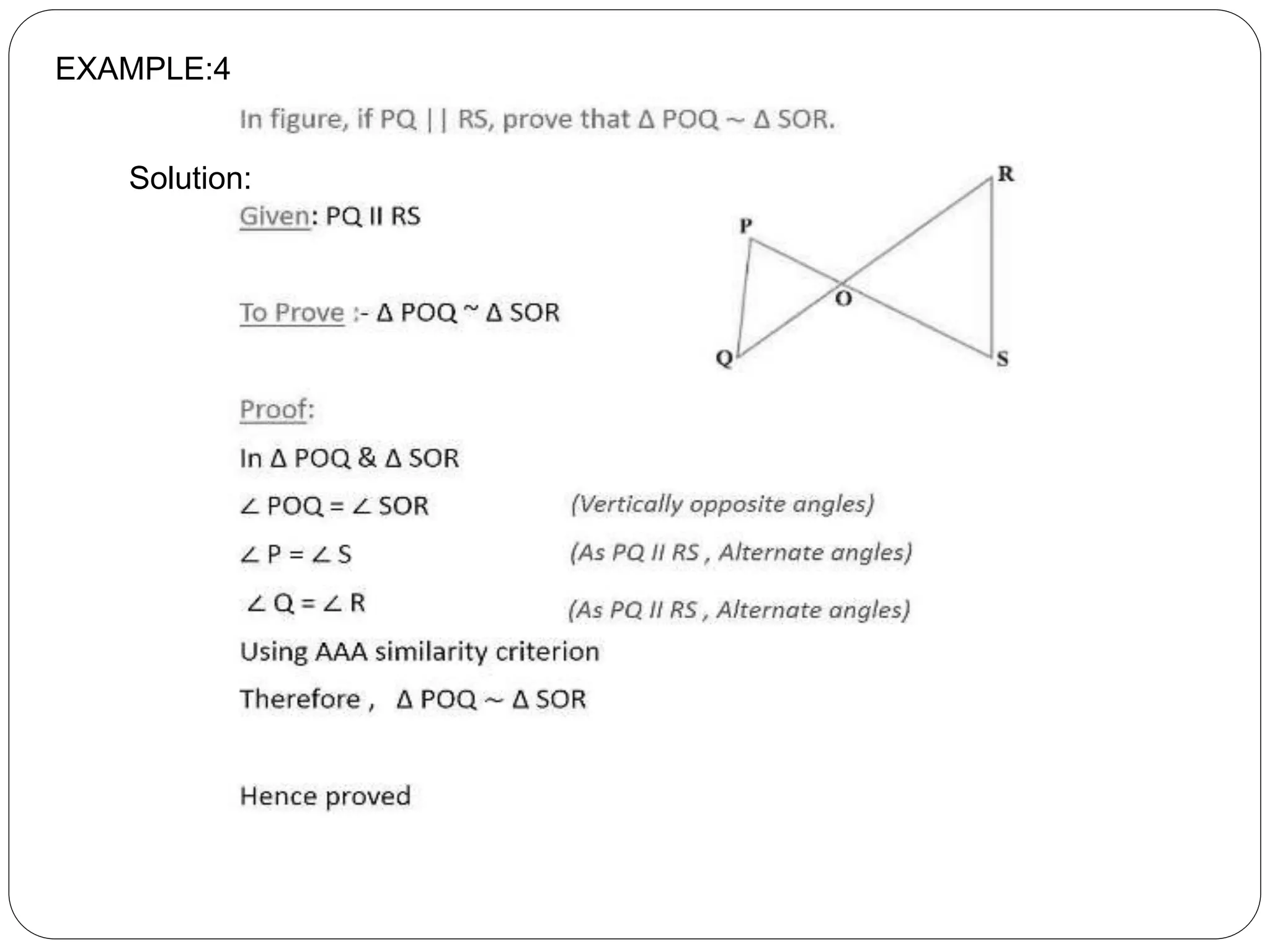
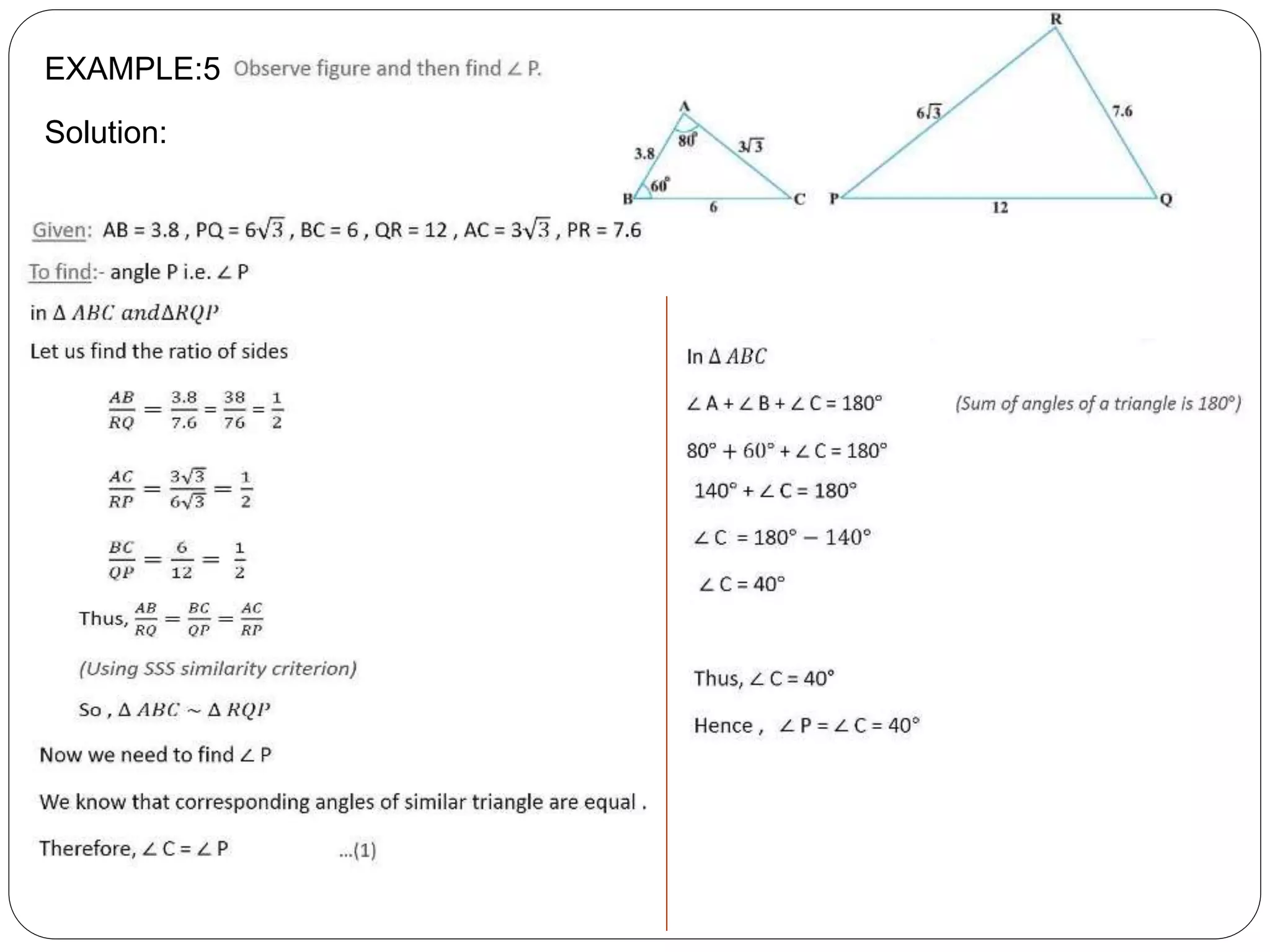
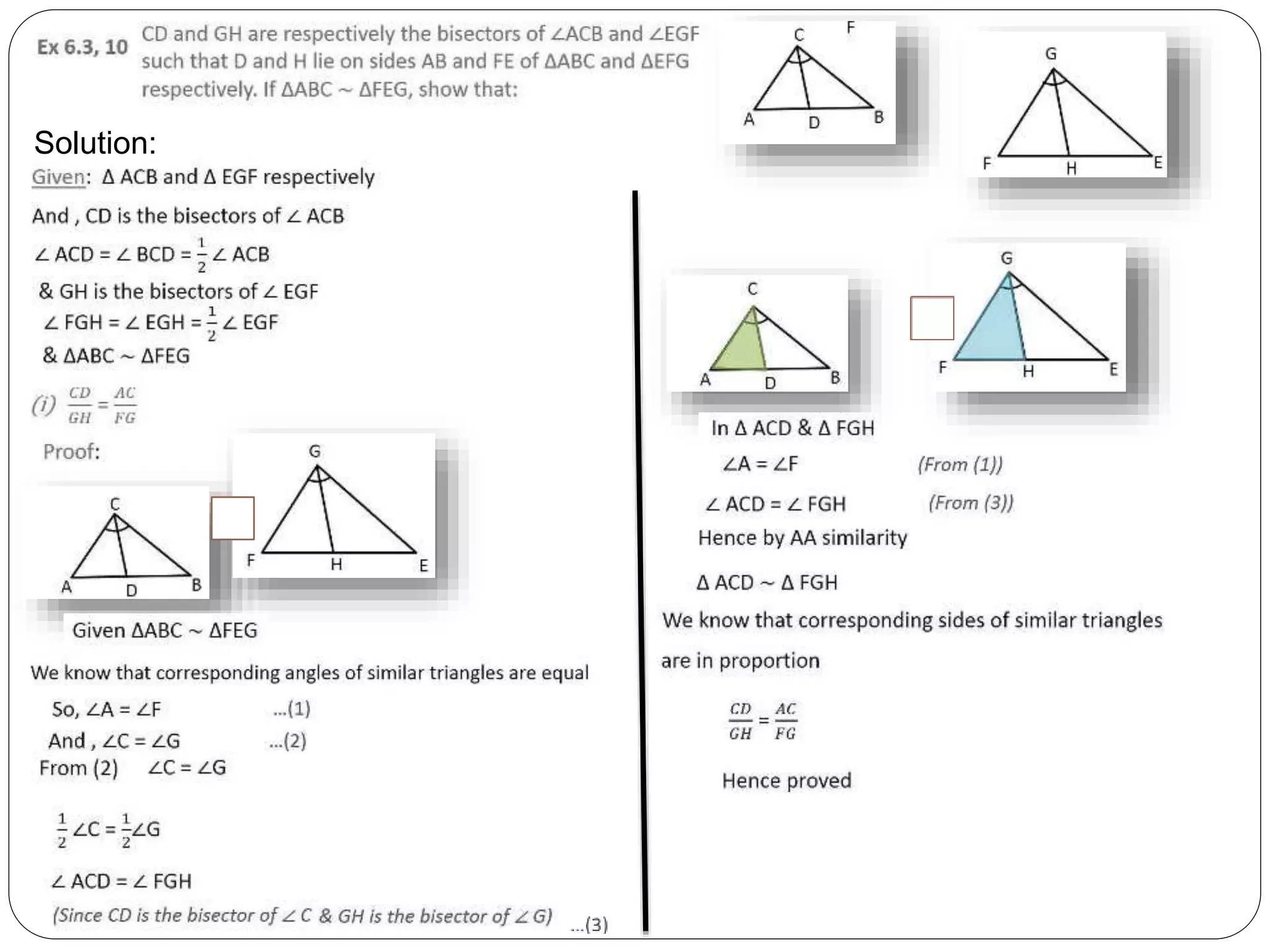
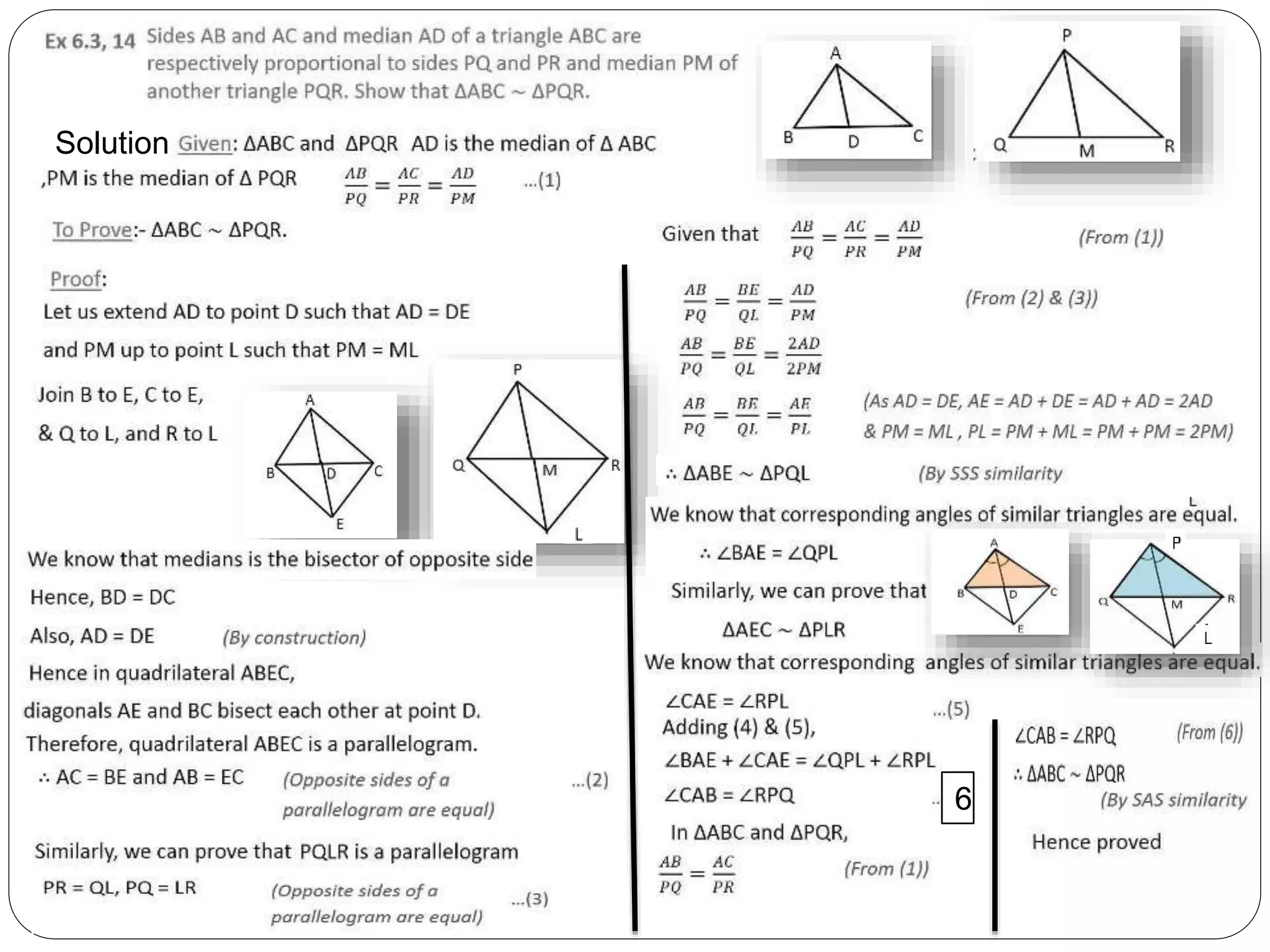
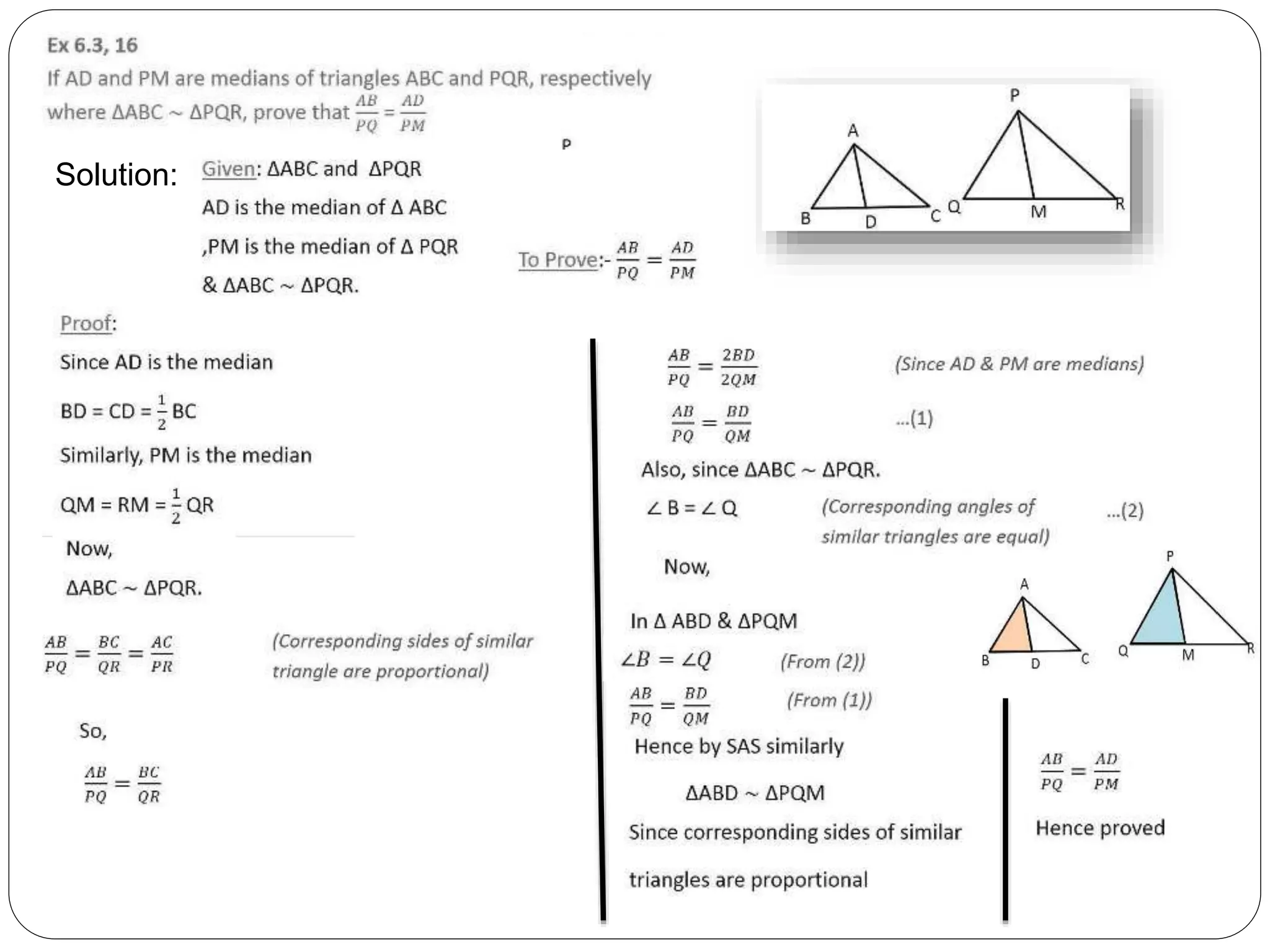
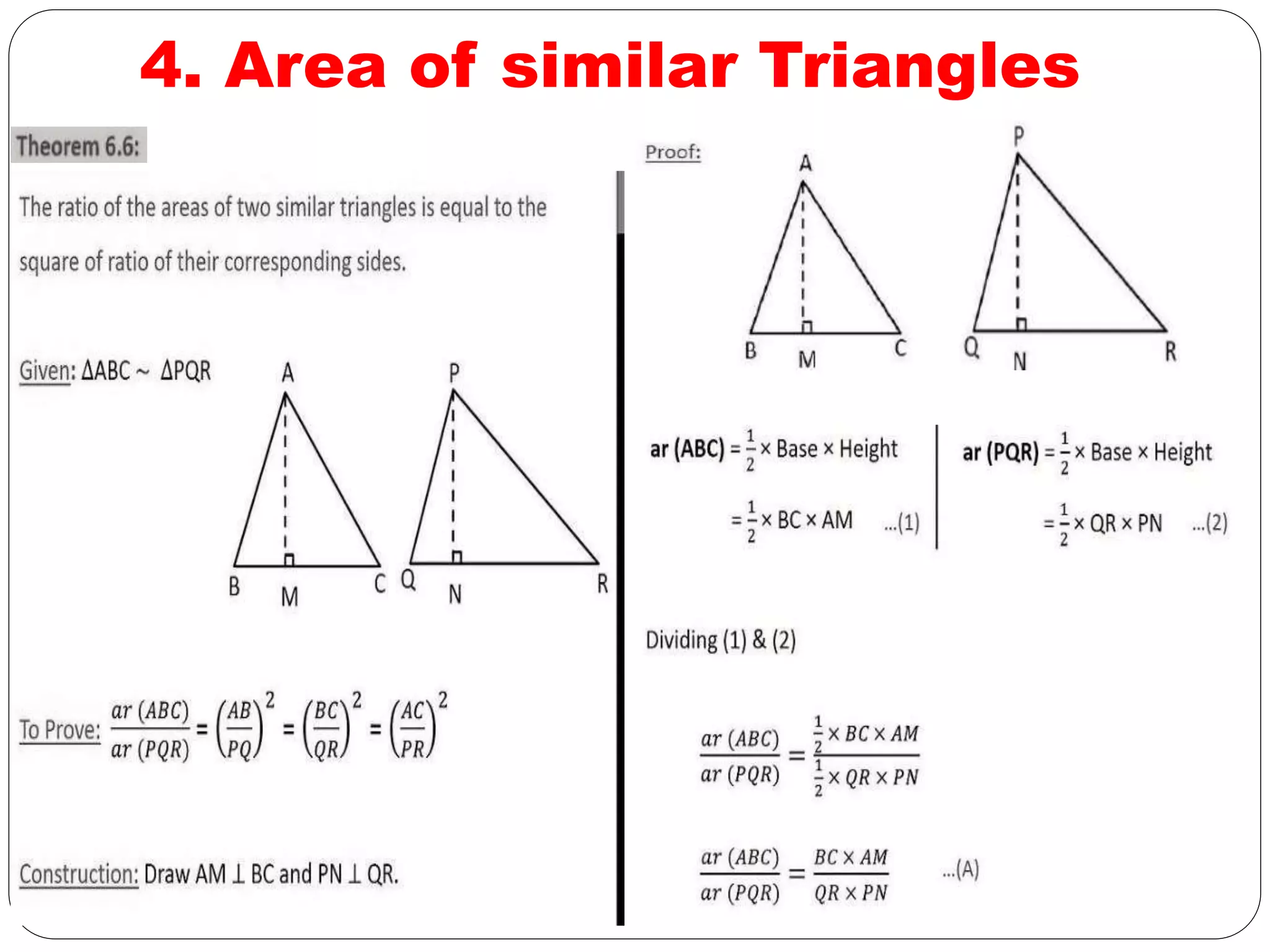
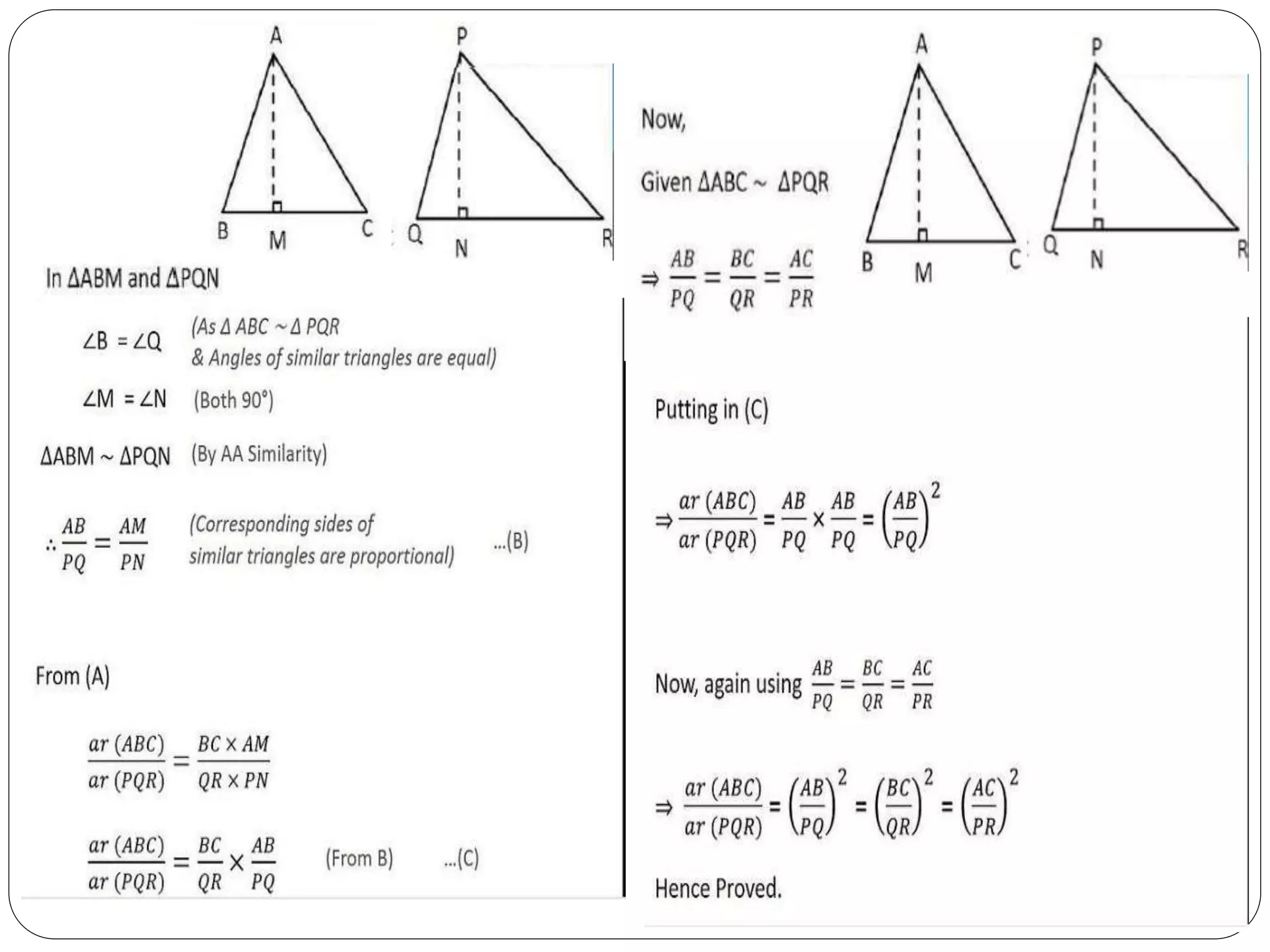
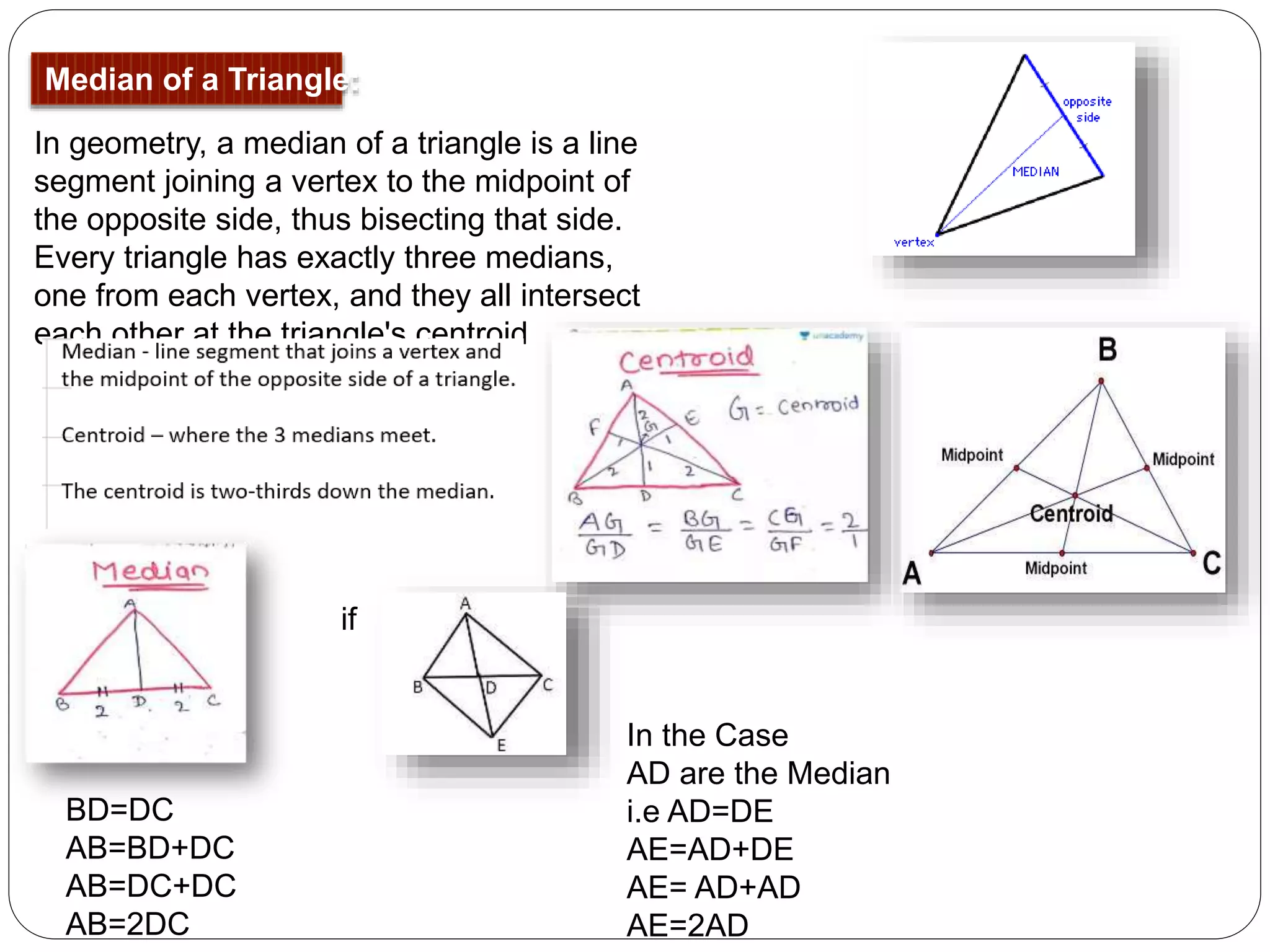
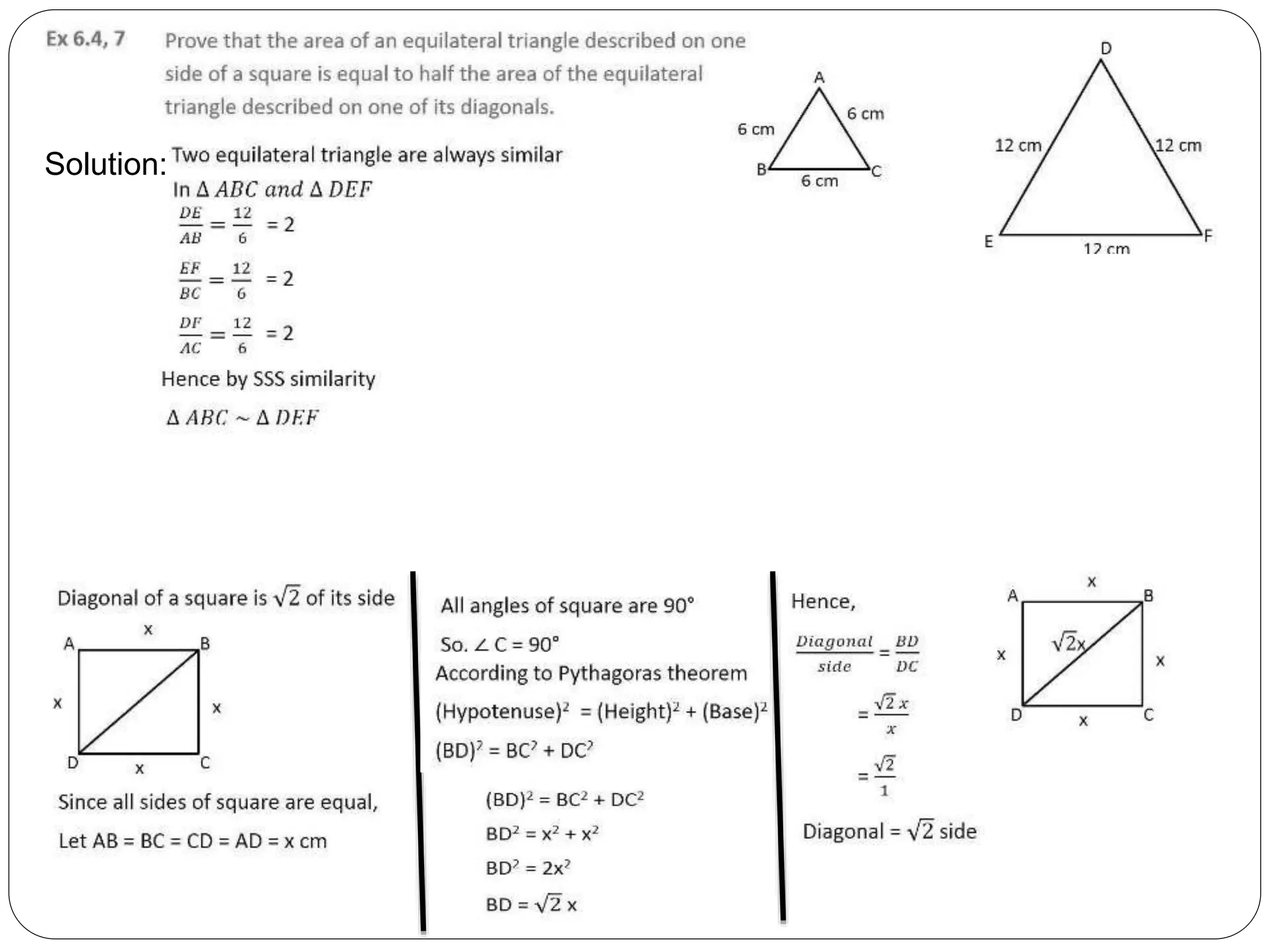
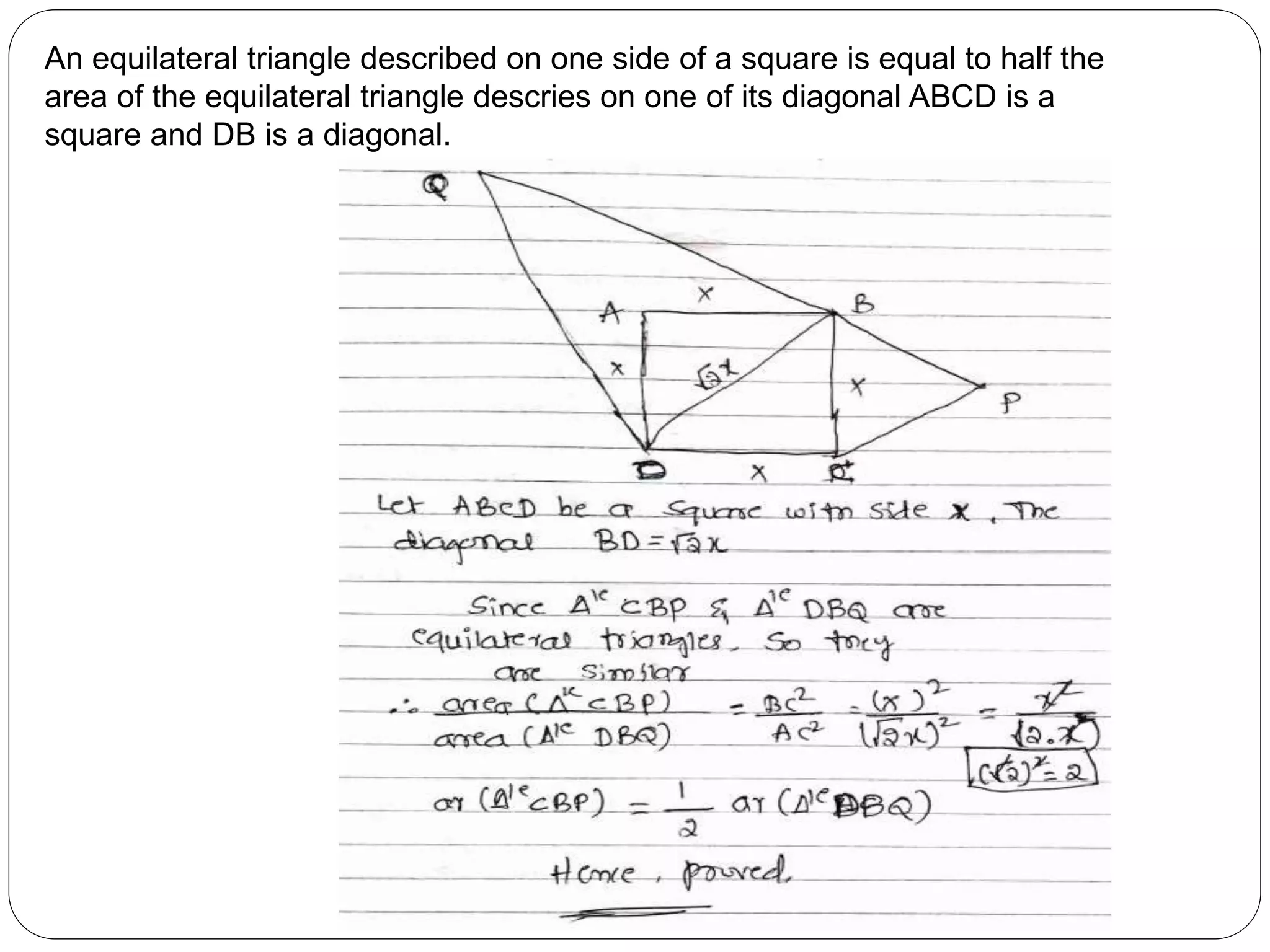
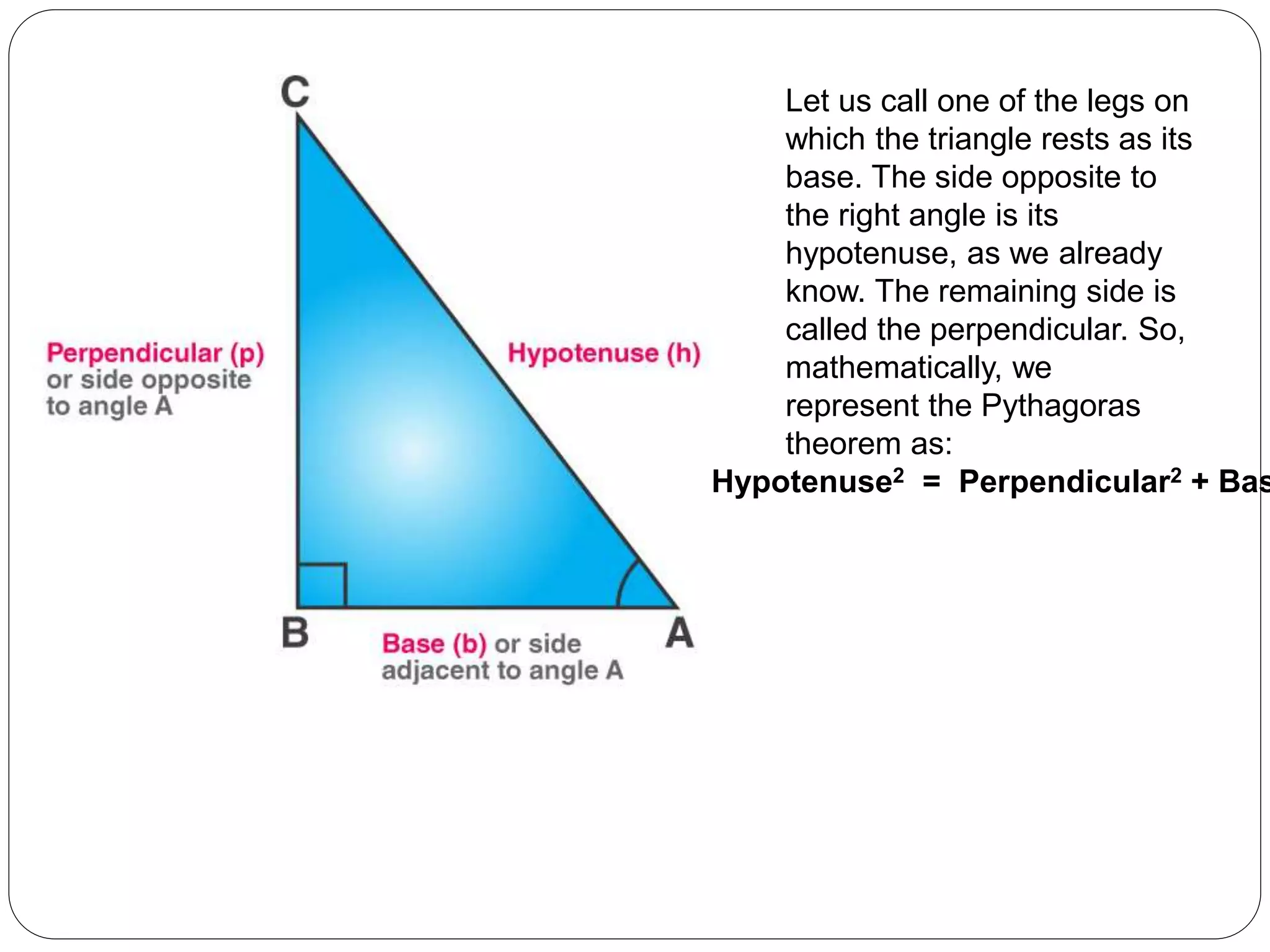
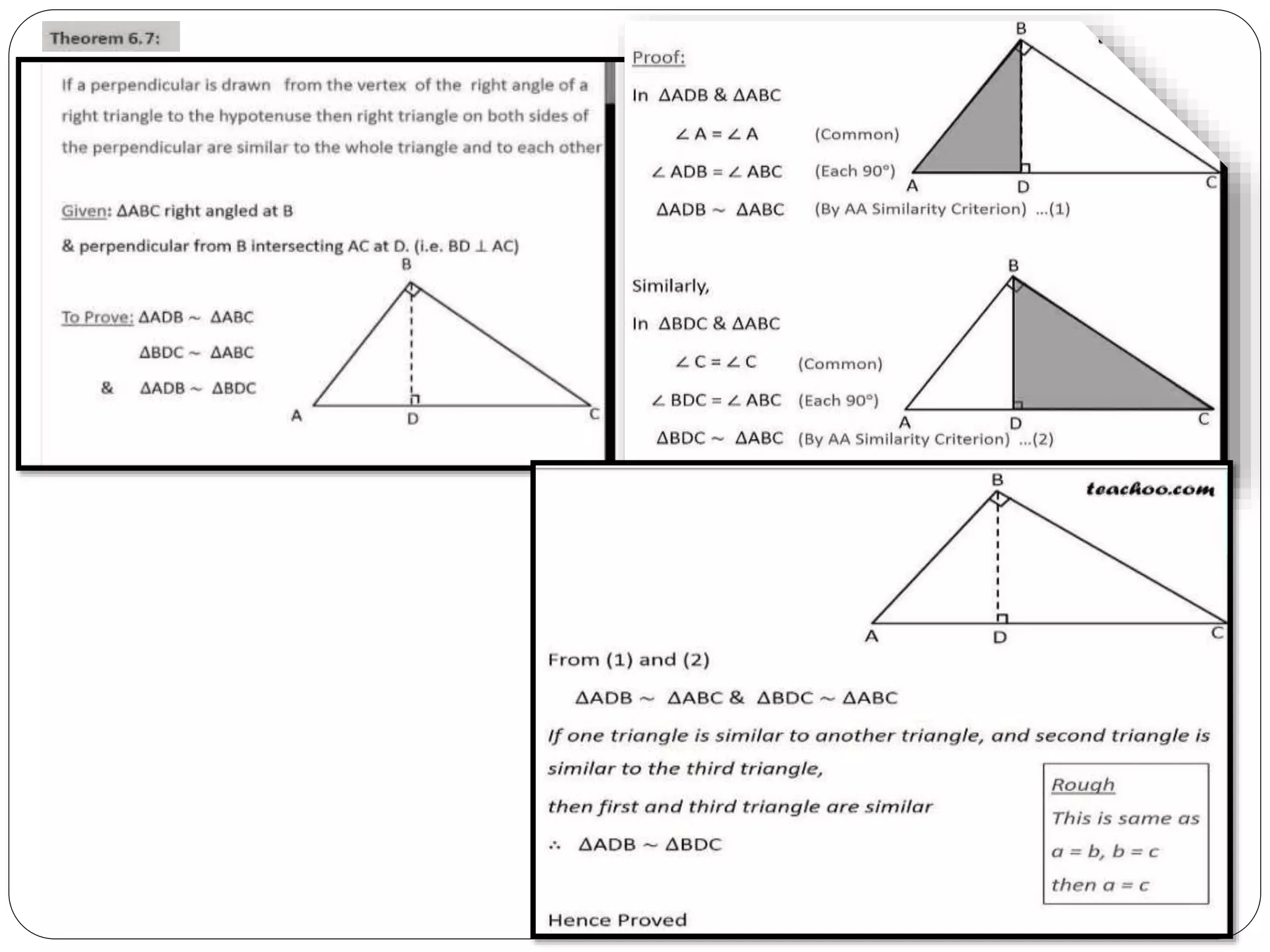
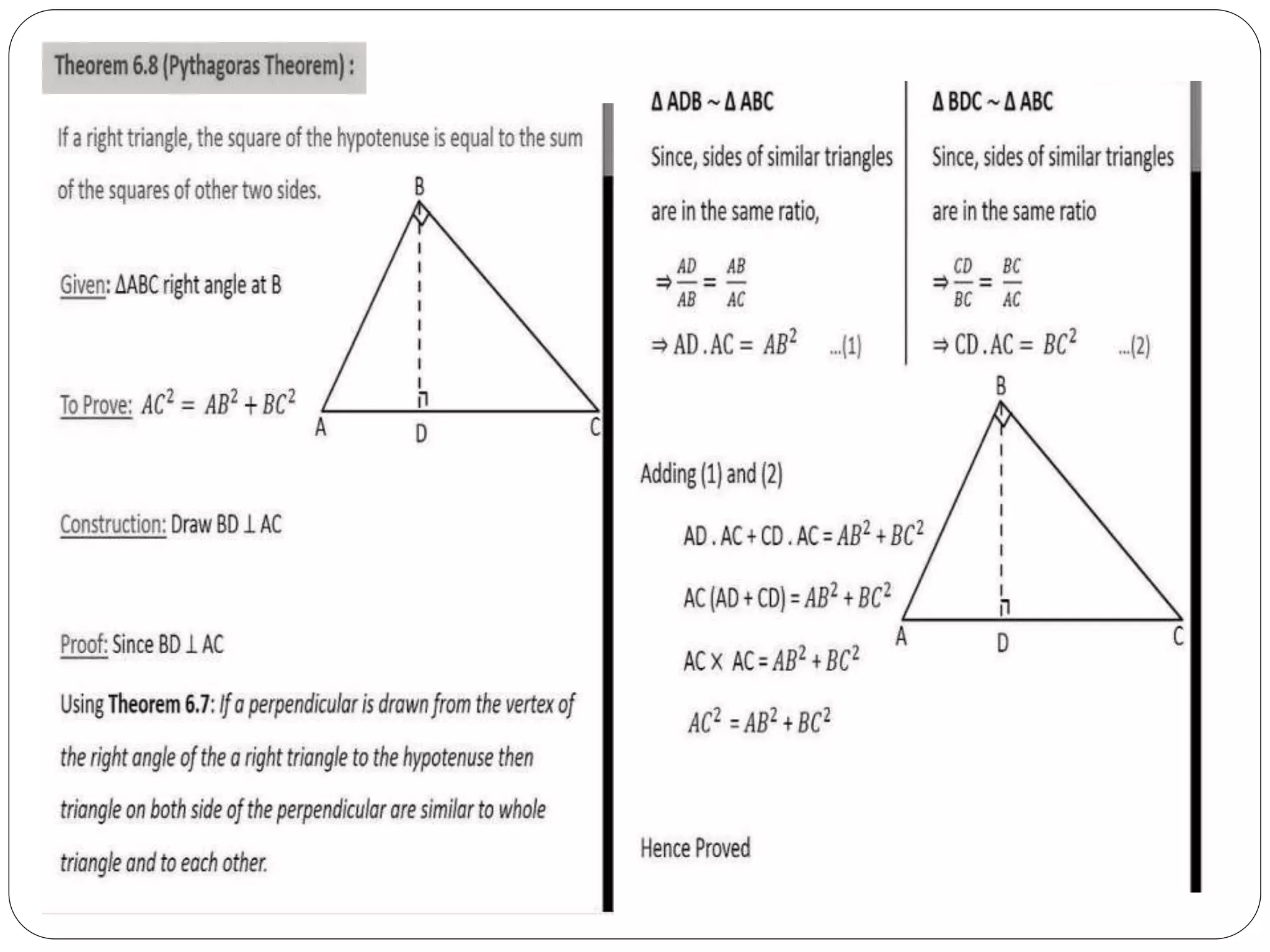
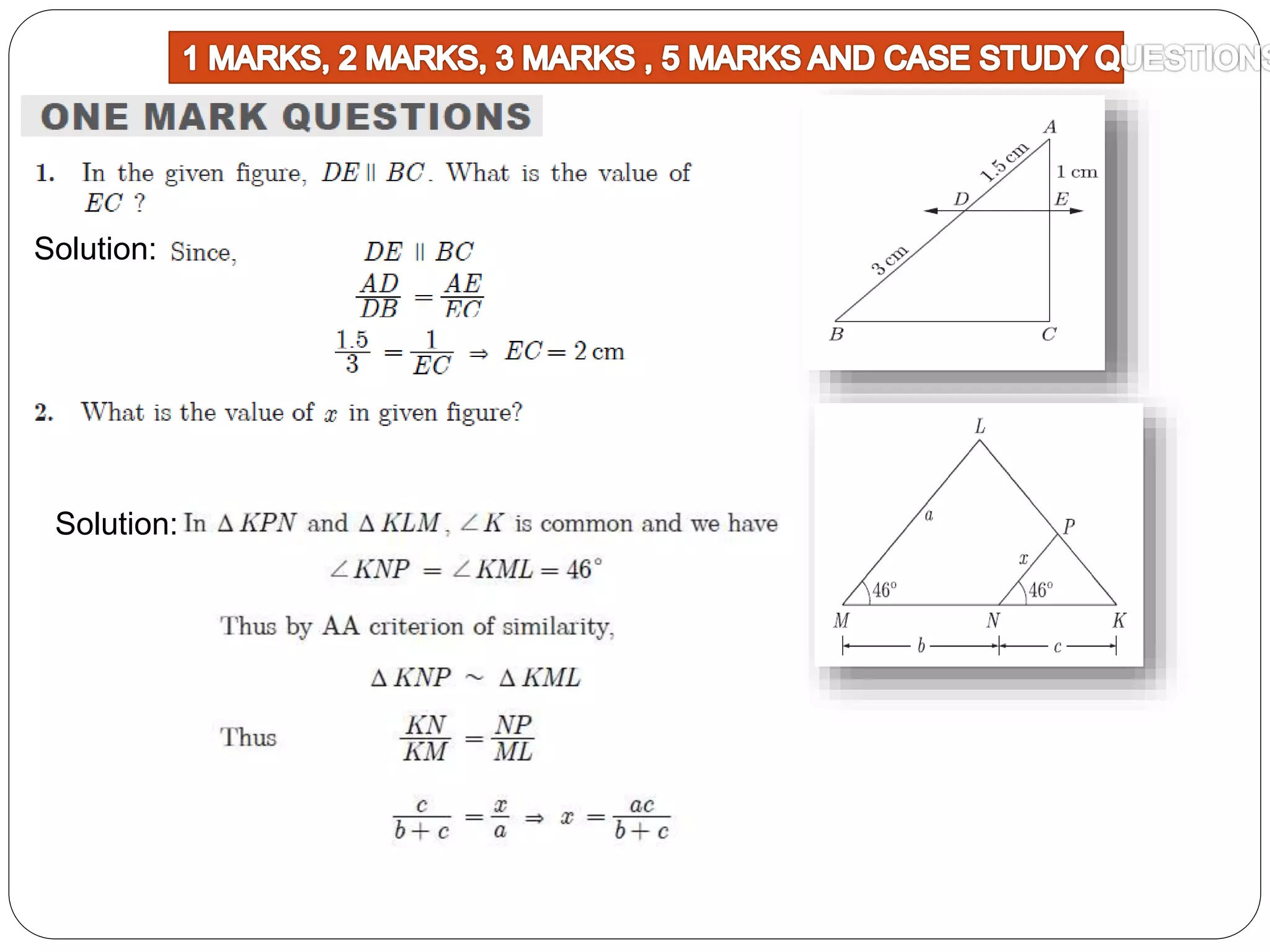
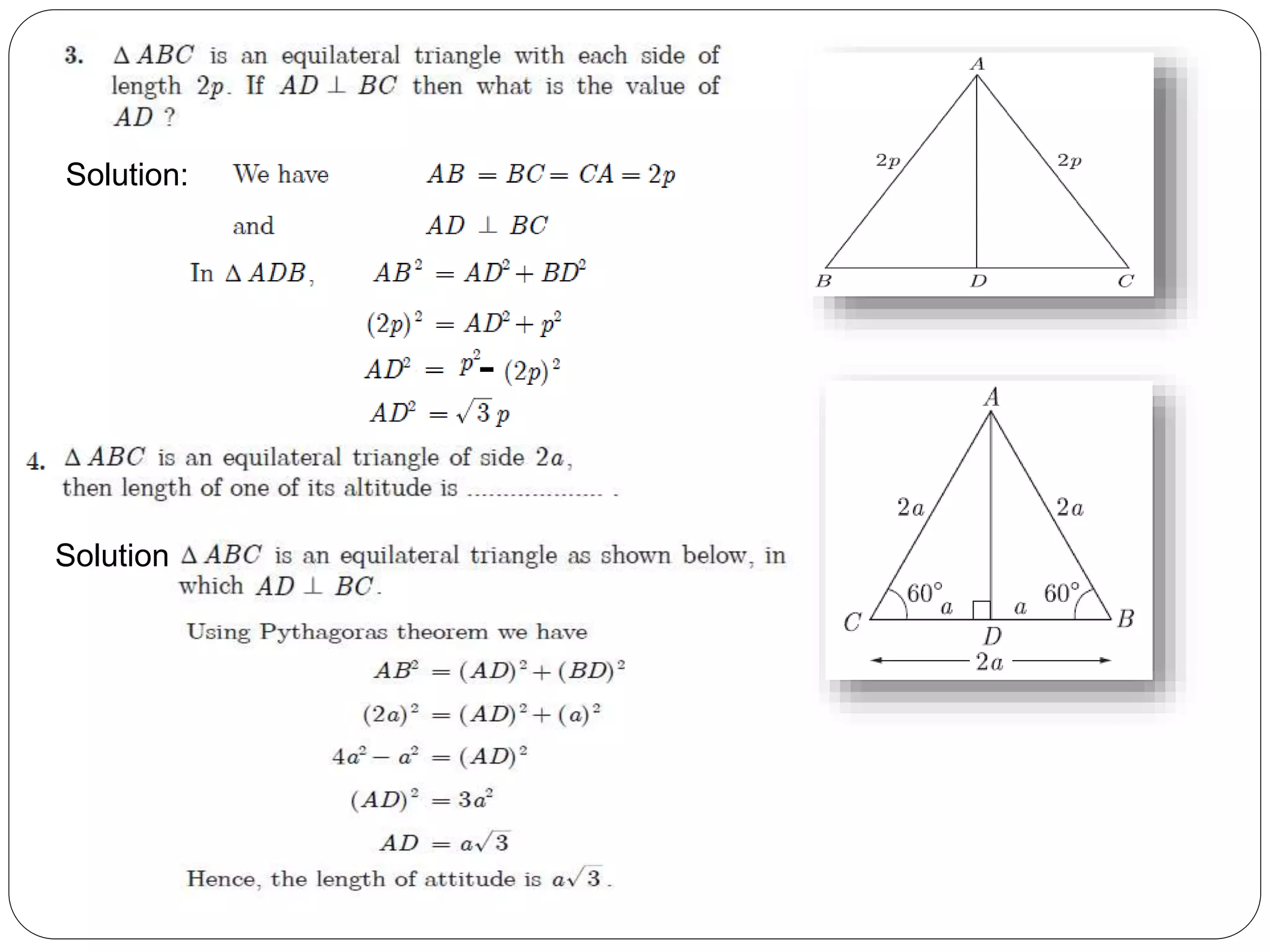
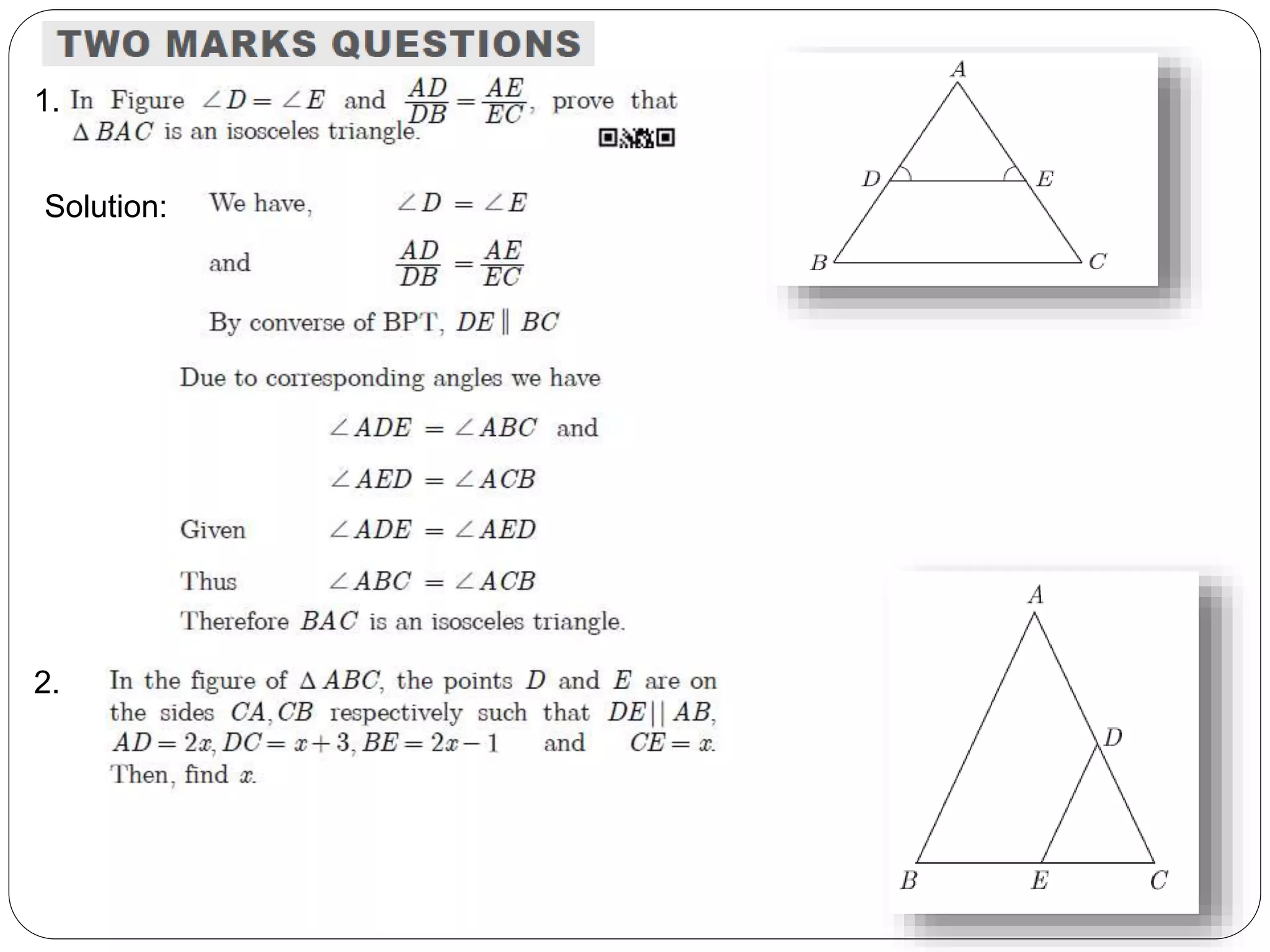
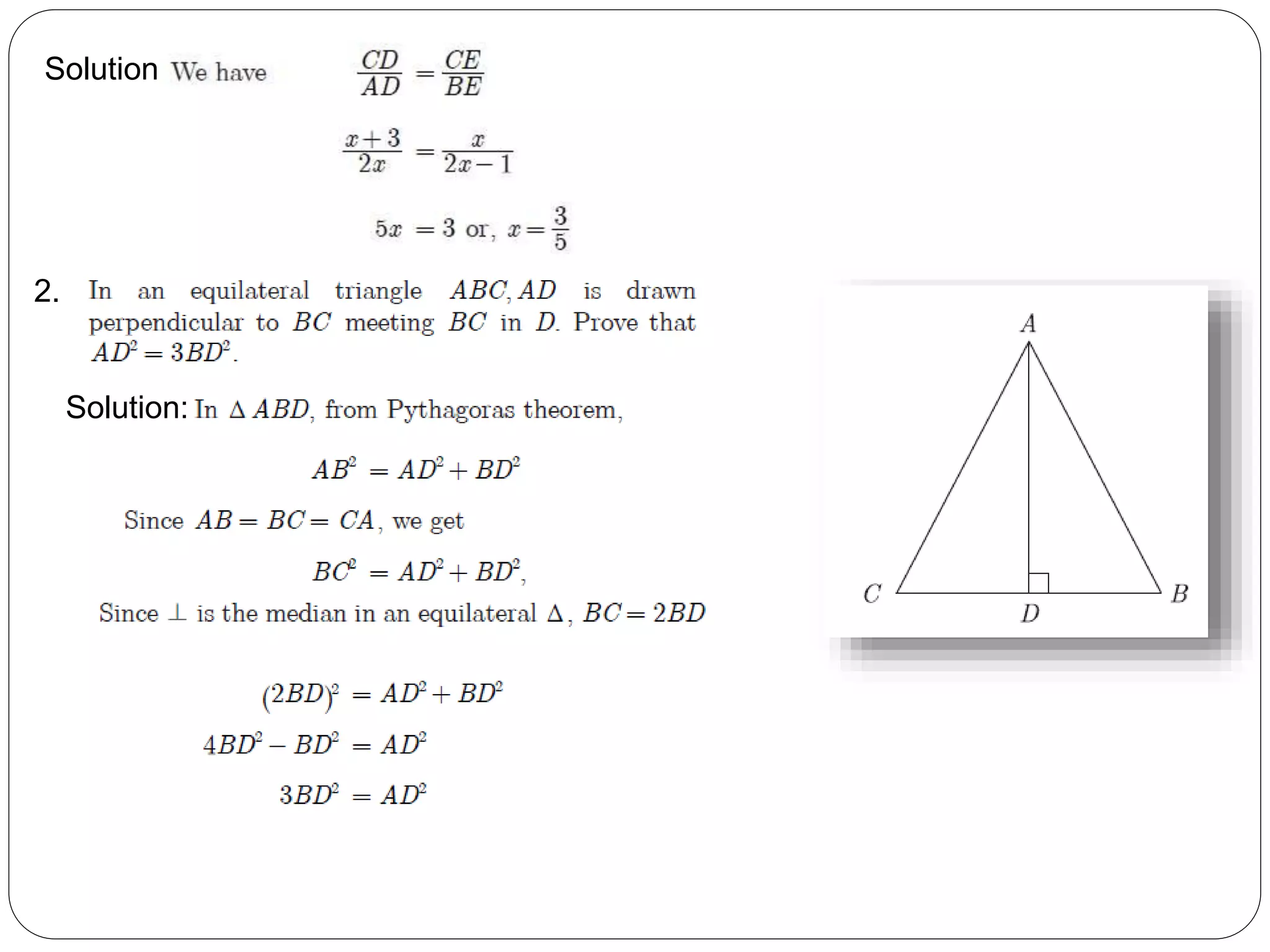
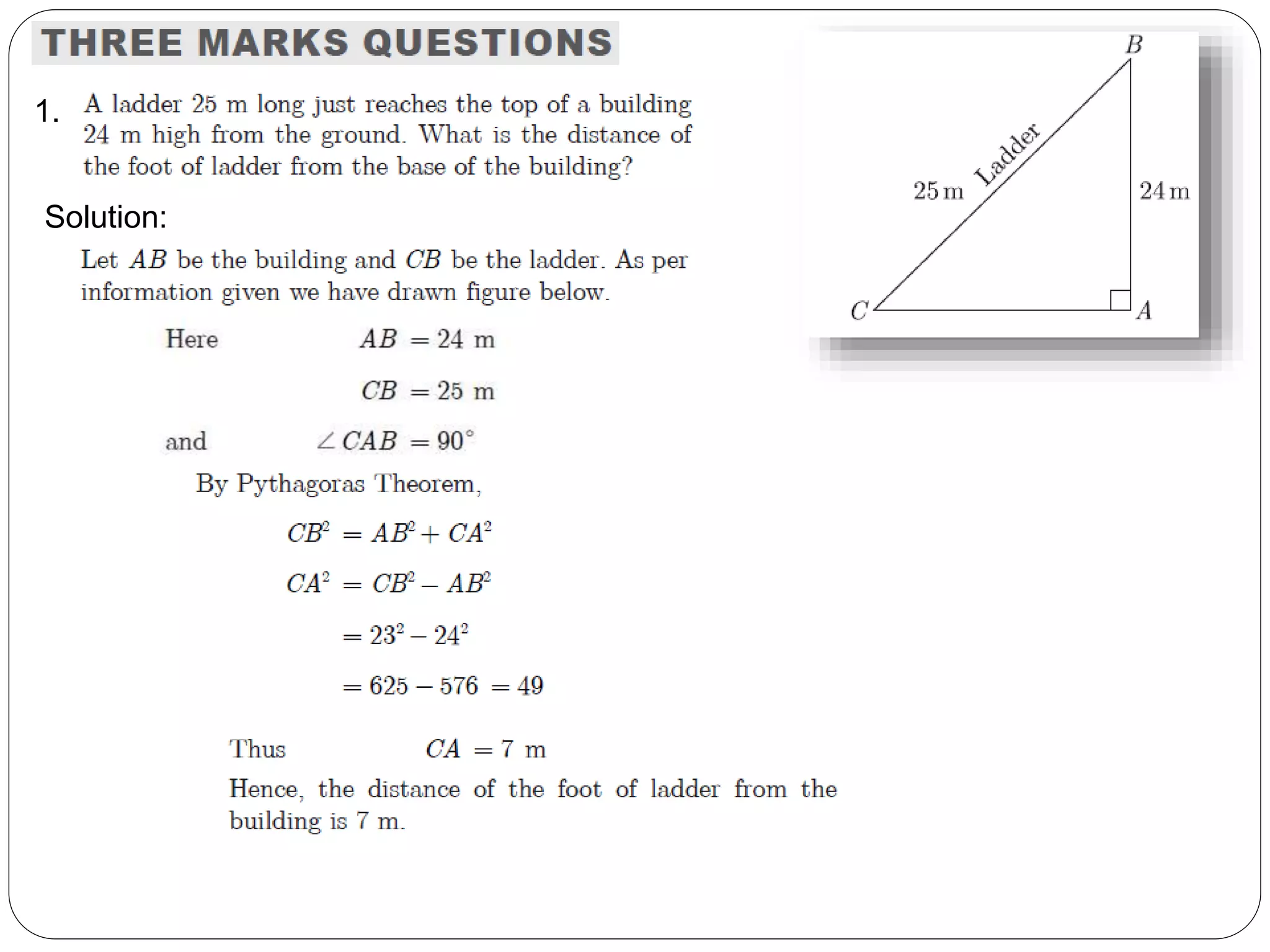
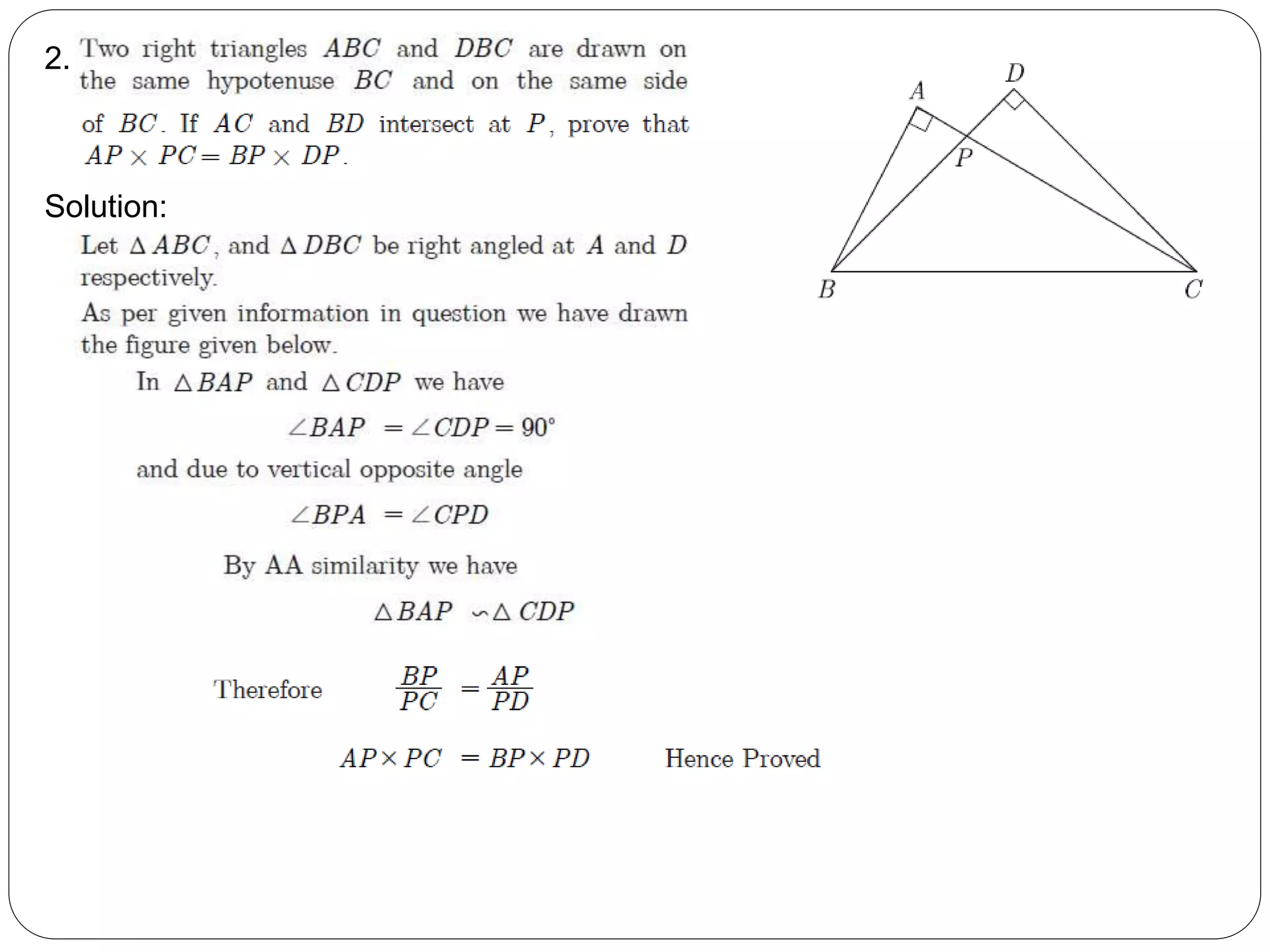
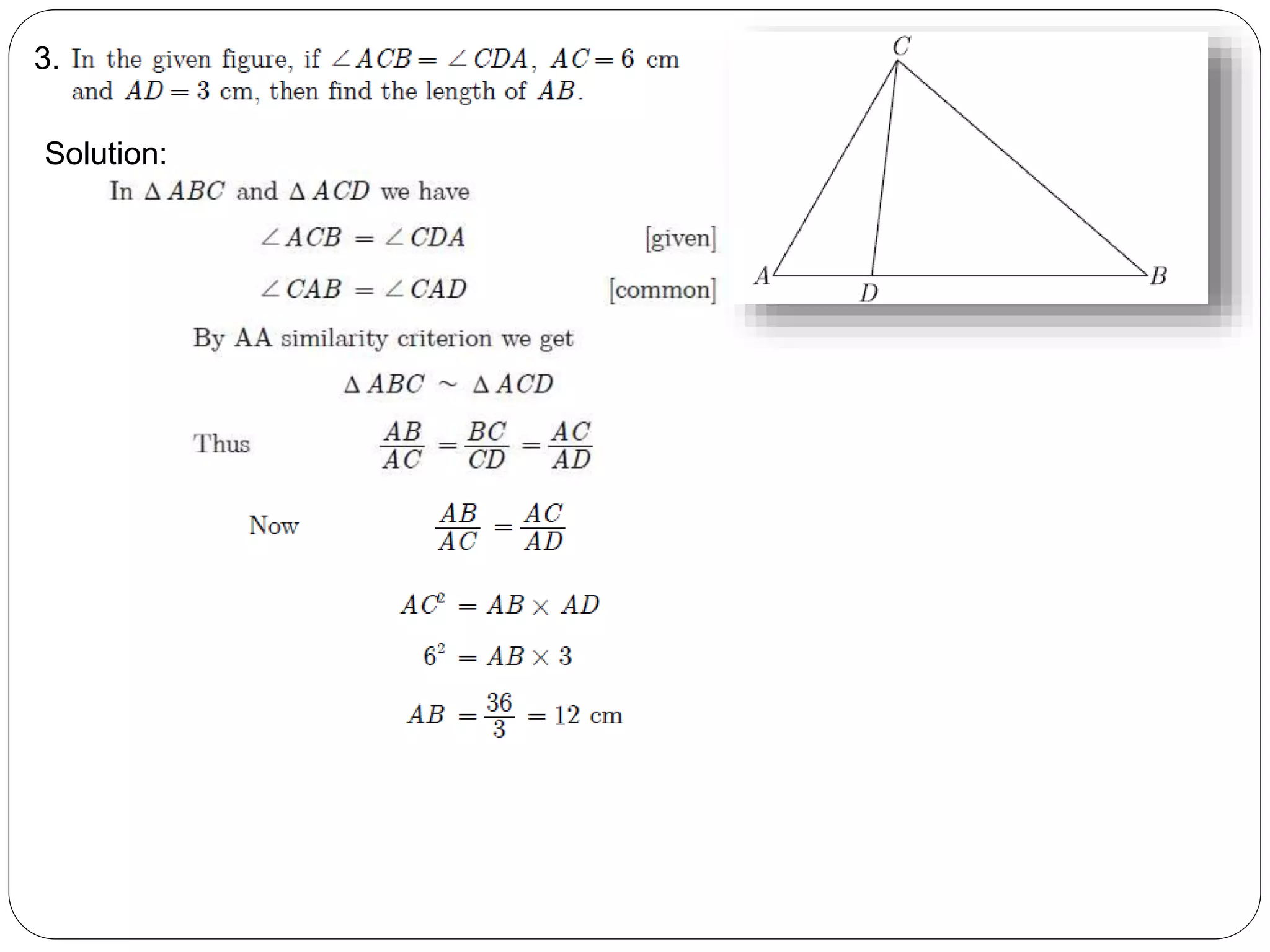
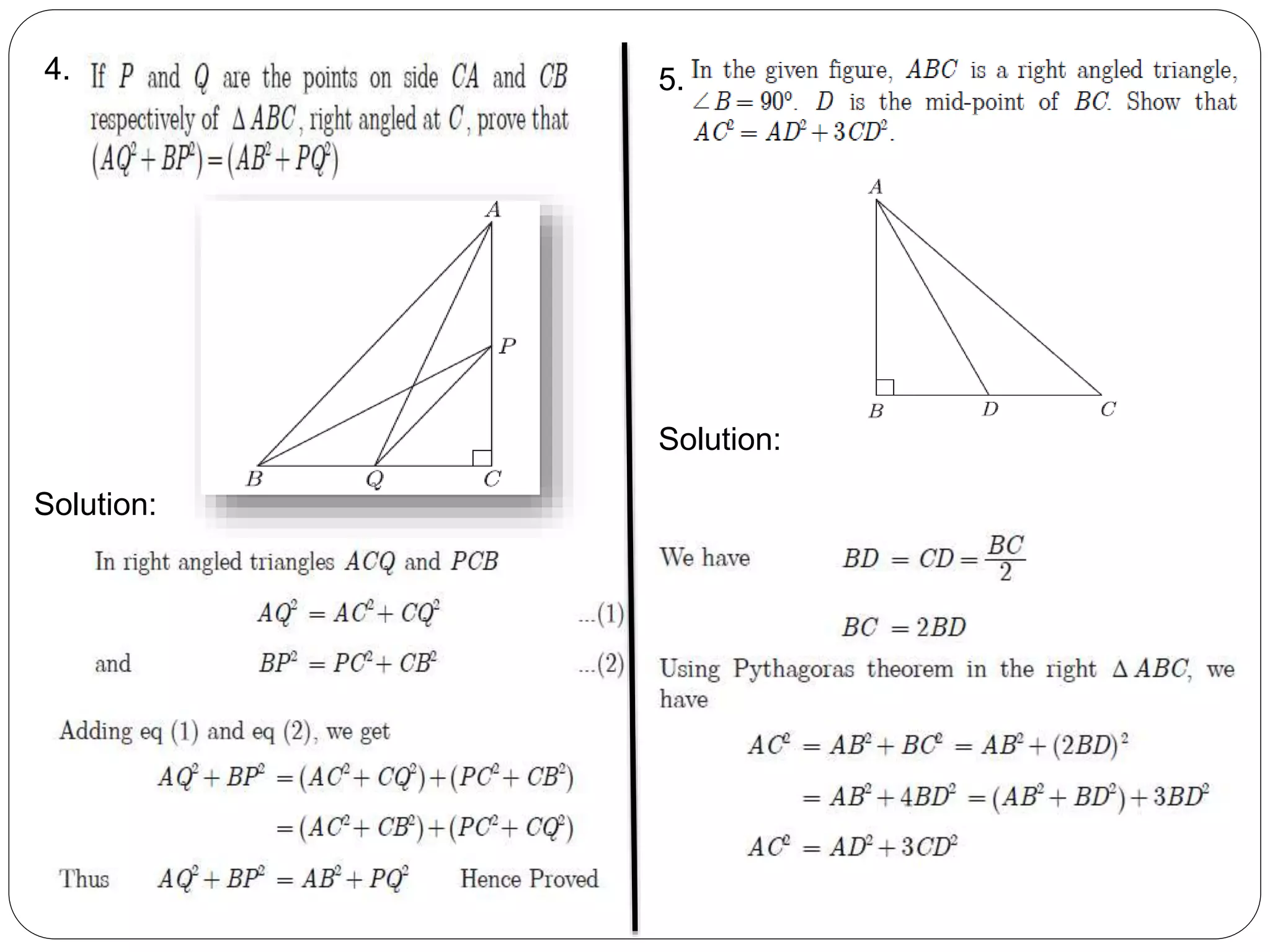
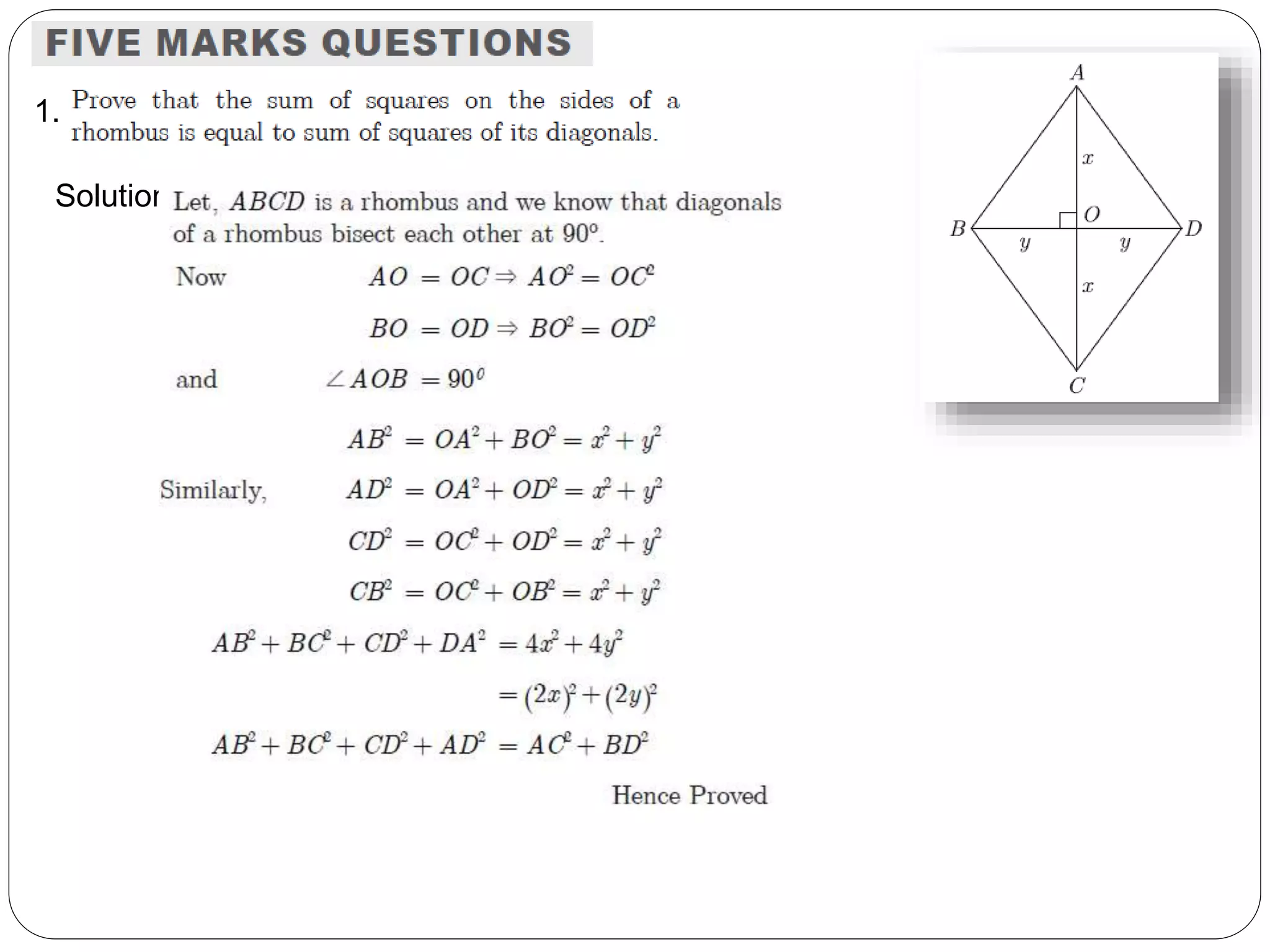
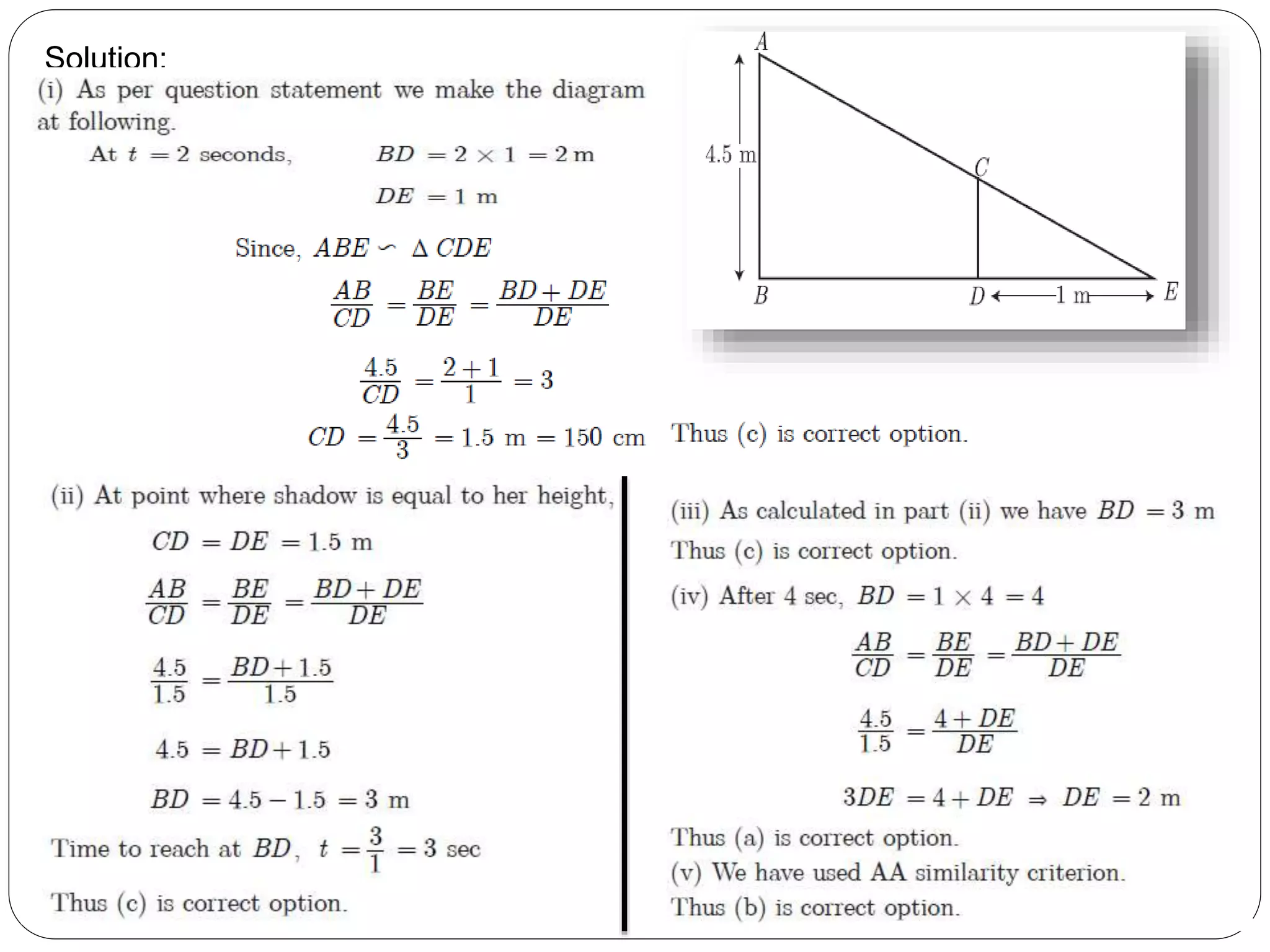
This document provides an overview of triangles, including their properties, types, similarity, areas of similar triangles, and the Pythagorean theorem. It defines triangles as polygons with three sides and angles, and notes their interior angles sum to 180 degrees. Triangles are classified by angle and side length into right, acute, obtuse, isosceles, equilateral, and scalene varieties. Similarity is discussed, along with criteria like equal angles and proportional sides. Areas of similar triangles are shown to be proportional to a ratio of corresponding sides. Finally, the Pythagorean theorem and its applications to find missing sides of right triangles are covered.

1. By
Sri.Siddalingeshwara BP M.Sc, B.Ed, (P.hd)
TRIANGLES
Chapter-6
For
Class-X

2. Content:
1.Introduction to Triangles
Properties of Triangles
Types of triangles
Polygons
Congruent
2.Similarity of Triangles (2 Theorem)
3.Criteria for Similarity of Triangles (3 Theorem)
4. Areas of Similar Triangles (1 Theorem)
5. Pythagoras Theorem (3 Theorem)

3. 1.Introduction to Triangles
 As the name suggests, the triangle is a polygon that has three angles.
So, when does a closed figure has three angles?
 When it has three line segments joined end to end.
 Thus, we can say that a triangle is a polygon, which has three sides,
three angles, three vertices and the sum of all three angles of any
triangle equals 1800.

5. Properties of Triangle.
 A triangle has three sides, three angles, and three vertices.
The sum of the length of any two sides of a triangle is greater
than the length of the third side.

6. • The sum of all internal angles of a triangle is always equal to 1800. This is called
the angle sum property of a triangle.
Example:

7. Types of Triangles
Triangles can be classified in 2 major ways:
 Classification according to internal angles
 Classification according to the length of its sides
By Length
 In geometry, an equilateral triangle is a triangle in which all three sides
have the same length.
 an isosceles triangle is a triangle that has two sides of equal length.

8. By Angle
1.one angle that measures
exactly 900
2. The side opposite to the
right angle is the largest side of
the triangle and is called the
hypotenuse.
all three angles less than 900
one angle that measures more than 900
Each interior angle of an
equilateral triangle = 60 degree

9. Polygon
1. A polygon is a closed plane figure with three or more
sides that are all straight.
2. Circle is a polygon? Ans: NO
Two polygon are said to be similar
a. They have same number of sides
b. Their corresponding angles are equal
c. All corresponding sides are in proportional i.e they
are in the same ratio.

10. Congruent
1. Two geometrical figures are said to be similar if they
have same shape but may or may not have same size.
2. Two geometrical figures are said to be congruent
they have same shape and same size.
3. All congruent figures are similar but all similar may
or may not be congruent.

11. EXERCISE 6.1

12. 2. Similarity of Triangles.
If two triangles are similar, if
1.Their corresponding angles are equal and
2. Their corresponding sides are in the same ratio (or Proportion)
“The ratio of any two corresponding sides in two equiangular triangles is
always the same” This is from basic proportionality theorem(BPT) known
as Thales Theorem. By Greek mathematician Thales.

13. To Understand BPT, Let us Perform the following ACTIVITY

15. C
(BPT Theorem)

19. ( Converse of BPT Theorem)

21. EXAMPLE 1:
Solution:

22. Example:2
Solution:
B

23. EXERCISE 6.2:
Solution:

24. Solution:

25. Solution:

26. 3.Criteria for Similarity of Triangles
D

28. Remark:

35. EXAMPLE:4
Solution:

36. EXAMPLE:5
Solution:

37. EXERCISE 6.3

39. Solution:

41. Solution:

42. Solution:

43. Solution:
6

44. Solution:

45. 4. Area of similar Triangles

47. Median of a Triangle:
In geometry, a median of a triangle is a line
segment joining a vertex to the midpoint of
the opposite side, thus bisecting that side.
Every triangle has exactly three medians,
one from each vertex, and they all intersect
each other at the triangle's centroid
In the Case
AD are the Median
i.e AD=DE
AE=AD+DE
AE= AD+AD
AE=2AD
if
BD=DC
AB=BD+DC
AB=DC+DC
AB=2DC

48. Solution:
(As form given

49. Solution:

50. Solution:

51. An equilateral triangle described on one side of a square is equal to half the
area of the equilateral triangle descries on one of its diagonal ABCD is a
square and DB is a diagonal.

52. 5 Pythagoras Theorem
 Pythagorean Theorem is one of the most fundamental theorems
in mathematics and it defines the relationship between the three
sides of a right-angled triangle. You are already aware of the
definition and properties of a right-angled triangle. It is the
triangle with one of its angles as a right angle, that is, 90 degrees.
The side that is opposite to the 90-degree angle is known as the
hypotenuse. The other two sides that are adjacent to the right
angle are called legs of the triangle.
 The Pythagoras theorem, also known as the Pythagorean
theorem, states that the square of the length of the hypotenuse is
equal to the sum of squares of the lengths of other two sides of
the right-angled triangle. Or, the sum of the squares of the two
legs of a right triangle is equal to the square of its hypotenuse.

53. Hypotenuse2 = Perpendicular2 + Bas
Let us call one of the legs on
which the triangle rests as its
base. The side opposite to
the right angle is its
hypotenuse, as we already
know. The remaining side is
called the perpendicular. So,
mathematically, we
represent the Pythagoras
theorem as:

57. Solution:

58. Summary:

59. Solution:
Solution:

60. Solution:
-
Solution:

61. Solution:
Solution:

62. 7.
Solution:
8.
Solution:

63. 1.
Solution:
2.

64. Solution:
2.
Solution:

65. 3.
Solution:

66. 1.
Solution:

67. 2.
Solution:

68. 3.
Solution:

69. 4.
Solution:
5.
Solution:

70. 1.
Solution:

71. 2.
Solution:

72. 1.

73. Solution:

74. References:
1. NCERT Text book
2. Google Source
THANK YOU