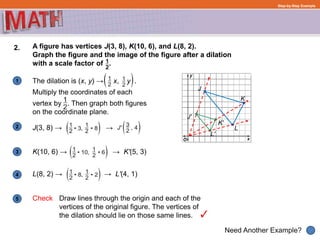
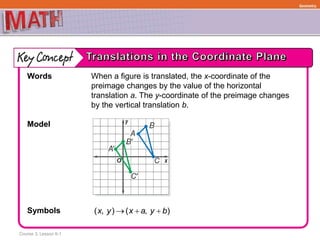
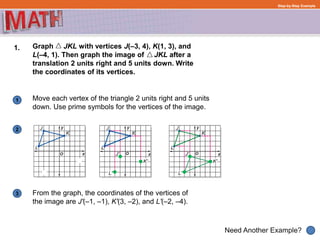
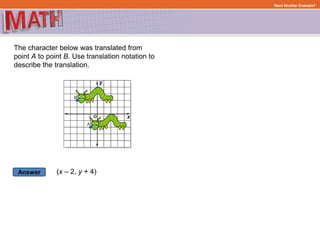
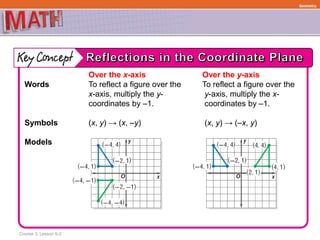
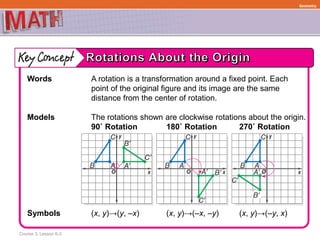
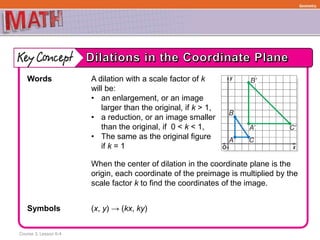
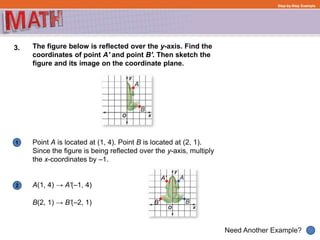
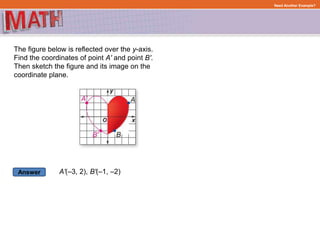
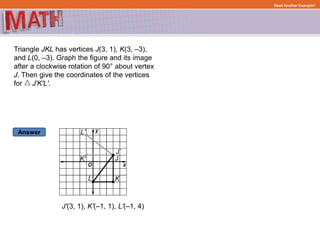
This document provides examples and explanations for describing geometric transformations on a coordinate plane, including translations, reflections, rotations, and dilations. It defines key terms like preimage, image, and scale factor. Examples show how to perform and describe each type of transformation by: 1) Graphing a figure and identifying its vertices with coordinates 2) Performing the transformation by applying the rules for that specific transformation 3) Graphing the transformed image and identifying the new coordinates of its vertices The document ensures understanding through multiple examples of each transformation type and encourages practicing the skills on additional example problems. It emphasizes that transformations preserve properties like distance and angle measures.

1. HOW can we best show or describe the
change in position of a figure?
Geometry
Course 3, Lesson 6-1

2. To
• translate a figure on the
coordinate plane
Course 3, Lesson 6-1
Geometry

3. Symbols
• transformation (x, y)  (x + a, y + b)
• preimage A’ is read A prime
• image
• translation
• congruent
Course 3, Lesson 6-1
Geometry

4. Course 3, Lesson 6-1
Geometry
Words When a figure is translated, the x-coordinate of the
preimage changes by the value of the horizontal
translation a. The y-coordinate of the preimage changes
by the vertical translation b.
Model
Symbols ( , ) ( , )x y x a y b  

5. 1
Need Another Example?
2
3
Step-by-Step Example
1. Graph JKL with vertices J(–3, 4), K(1, 3), and
L(–4, 1). Then graph the image of JKL after a
translation 2 units right and 5 units down. Write
the coordinates of its vertices.
Move each vertex of the triangle 2 units right and 5 units
down. Use prime symbols for the vertices of the image.
From the graph, the coordinates of the vertices of
the image are J'(–1, –1), K'(3, –2), and L'(–2, –4).

6. Answer
Need Another Example?
Graph ABC with vertices A(–2, 2), B(3, 4),
and C(4, 1). Then graph the image of ABC
after a translation 2 units left and 5 units
down. Write the coordinates of its vertices.
A'(–4, –3),
B'(1, –1),
C'(2, –4)

7. 1
Need Another Example?
2
3
Step-by-Step Example
2. Triangle XYZ has vertices X(–1, –2), Y(6, –3) and
Z(2, –5). Find the vertices of X'Y'Z' after a
translation of 2 units left and 1 unit up.
Use a table. Add –2 to the x-coordinates and 1 to
the y-coordinates.
So, the vertices of X'Y'Z' are X'(–3, –1), Y'(4, –2),
and Z'(0, –4).

8. Answer
Need Another Example?
Rectangle ABCD has vertices A(–3, 2),
B(2, 2), C(2, –3), and D(–3, –3). Find the
vertices of rectangle A'B'C'D' after a
translation of 4 units right and 2 units down.
A'(1, 0), B'(6, 0), C'(6, –5), D'(1, –5)

9. 1
Need Another Example?
2
3
4
5
6
Step-by-Step Example
3. A computer image is being translated to create the
illusion of movement. Use translation notation to
describe the translation from point A to point B.
Point A is located at (3, 3). Point B is located at (2, 1).
(x, y) (x + a, y + b)
(3, 3) (3 + a, 3 + b) (2, 1)
3 + a = 2 3 + b = 1
a = –1 b = –2
So, the translation is (x – 1, y – 2), 1 unit to the left and
2 units down.

10. Answer
Need Another Example?
The character below was translated from
point A to point B. Use translation notation to
describe the translation.
(x – 2, y + 4)

11. To
• reflect a figure over the x-axis,
• reflect a figure over the y-axis
Course 3, Lesson 6-2
Geometry

12. • reflection
• line of reflection
Symbols
•(x, y)  (x, −y)
•(x, y)  (− x, y)
Course 3, Lesson 6-2
Geometry

13. Course 3, Lesson 6-2
Geometry
Over the x-axis Over the y-axis
Words To reflect a figure over the To reflect a figure over the
x-axis, multiply the y- y-axis, multiply the x-
coordinates by –1. coordinates by –1.
Symbols (x, y) → (x, –y) (x, y) → (–x, y)
Models

14. 1
Need Another Example?
2
3
Step-by-Step Example
1. Triangle ABC has vertices A(5, 2), B(1, 3), and
C(–1, 1). Graph the figure and its reflected image
over the x-axis. Then find the coordinates of the
vertices of the reflected image.
The x-axis is the line of reflection. So, plot each vertex
of A'B'C' the same distance from the x-axis as its
corresponding vertex on ABC.
The coordinates are A'(5, –2), B'(1, –3), and C'(–1, –1).
A'
B'
C'
Point A is 2 units above
the x-axis, …
… so point A' is plotted 2
units below the x-axis

15. Answer
Need Another Example?
Quadrilateral QRST has vertices Q(–1, 1), R(0, 3),
S(3, 2), and T(4, 0). Graph the figure and its
reflected image over the x-axis. Then find the
coordinates of the vertices of the reflected image.
Q'(–1, –1), R'(0, –3), S'(3, –2), T'(4, 0)

16. 1
Need Another Example?
2
3
Step-by-Step Example
2. Quadrilateral KLMN has vertices K(2, 3), L(5, 1),
M(4, –2), and N(1, –1). Graph the figure and its
reflection over the y-axis. Then find the coordinates
of the vertices of the reflected image.
The y-axis is the line of reflection. So, plot each vertex
of K'L'M'N' the same distance from the y-axis as its
corresponding vertex on KLMN.
The coordinates are K'(–2, 3), L'(–5, 1), M'(–4, –2), and N'(–1, –1).
Point K' is 2 units
to the left of the
y-axis.
Point K is 2 units
to the right of the
y-axis.
K'
L'
M'
N'

17. Answer
Need Another Example?
Triangle XYZ has vertices X(1, 2), Y(2, 1), and
Z(1, –2). Graph the figure and its reflected
image over the y-axis. Then find the coordinates
of the vertices of the reflected image.
X'(–1, 2), Y'(–2, 1), Z'(–1, –2)

18. 1
Need Another Example?
2
Step-by-Step Example
3. The figure below is reflected over the y-axis. Find the
coordinates of point A' and point B'. Then sketch the
figure and its image on the coordinate plane.
Point A is located at (1, 4). Point B is located at (2, 1).
Since the figure is being reflected over the y-axis, multiply
the x-coordinates by –1.
A(1, 4) → A'(–1, 4)
B(2, 1) → B'(–2, 1)
A'
B'

19. Answer
Need Another Example?
The figure below is reflected over the y-axis.
Find the coordinates of point A' and point B'.
Then sketch the figure and its image on the
coordinate plane.
A'(–3, 2), B'(–1, –2)

20. Course 3, Lesson 6-3
Use the act it out strategy to solve Exercises 1–3.
1. Four friends all shake hands with one another. How many
handshakes take place?
2. Liz's house is 4 blocks east and 2 blocks south from best
friend's house. Her school is 2 blocks west and 5 blocks
north of her house. What is one way she can travel from her
friend's house to school?
3. Max, Bud, David, and Anna are a team playing tug-of-war. In
how many different ways can they be arranged?

21. Course 3, Lesson 6-3
ANSWERS
1. 24
2. 6 blocks west and then 7 blocks north
3. 120

22. HOW can we best show or describe
the change in position of a figure?
Geometry
Course 3, Lesson 6-3

23. Course 3, Lesson 6-3 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices
and Council of Chief State School Officers. All rights reserved.
Geometry
• 8.G.1
Verify experimentally the properties of rotations, reflections, and
translations:
• 8.G.3
Describe the effect of dilations, translations, rotations, and
reflections on two-dimensional figures using coordinates.
Mathematical Practices
1 Make sense of problems and persevere in solving them.
3 Construct viable arguments and critique the reasoning of others.
4 Model with mathematics.
7 Look for and make use of structure.

24. To
• rotate a figure about a point,
• rotate a figure about the origin
Course 3, Lesson 6-3
Geometry

25. • rotation
• center of rotation
Symbols
• (x, y)  (y, −x)
• (x, y)  (−x, − y)
• (x, y)  (− y, x)
Course 3, Lesson 6-3
Geometry

26. 1
Need Another Example?
2
3
4
Step-by-Step Example
1. Triangle LMN with vertices L(5, 4), M(5, 7), and N(8, 7)
represents a desk in Jackson's bedroom. He wants to
rotate the desk counterclockwise 180° about vertex L.
Graph the figure and its image. Then give the coordinates
of the vertices for L'M'N'.
Graph the original triangle.
Repeat Step 2 for point N. Since L is the point at which
LMN is rotated, L' will be in the same position as L.
So, the coordinates of the vertices of L'M'N' are
L'(5, 4), M'(5, 1), and N'(2, 1).
M N
LGraph the rotated image. Use
a protractor to measure an
angle of 180° with M as one
point on the ray and L as the
vertex. Mark off a point the
same length as ML. Label
this point M' as shown.
L'
M'
180°
N'

27. Answer
Need Another Example?
Triangle JKL has vertices J(3, 1), K(3, –3),
and L(0, –3). Graph the figure and its image
after a clockwise rotation of 90° about vertex
J. Then give the coordinates of the vertices
for J'K'L'.
J'(3, 1), K'(–1, 1), L'(–1, 4)

28. Course 3, Lesson 6-3
Geometry
Words A rotation is a transformation around a fixed point. Each
point of the original figure and its image are the same
distance from the center of rotation.
Models The rotations shown are clockwise rotations about the origin.
90˚ Rotation 180˚ Rotation 270˚ Rotation
Symbols (x, y)→(y, –x) (x, y)→(–x, –y) (x, y)→(–y, x)

29. 1
Need Another Example?
2
3
4
Step-by-Step Example
2. Triangle DEF has vertices D(–4, 4), E(–1, 2), and
F(–3, 1). Graph the figure and its image after a clockwise
rotation of 90° about the origin. Then give the coordinates
of the vertices for D'E'F'.
Graph DEF on a coordinate plane.
Repeat Step 2 for points D and F.
Then connect the vertices to
form D'E'F'.
So, the coordinates of the vertices
of D'E'F' are D'(4, 4), E'(2, 1),
and F'(1, 3).
Sketch segment EO connecting
point E to the origin. Sketch
another segment, E'O, so that the
angle between point E, O, and E'
measures 90° and the segment is
the same length as EO.
D
E
F E'
D'
F'

30. Answer
Need Another Example?
Triangle ABC has vertices A(–4, 1), B(–1, 4),
and C(–2, 1). Graph the figure and its image after a
counterclockwise rotation of 180° about the origin.
Then give the coordinates of the vertices for A'B'C'.
A'(4, –1),
B'(1, –4),
C'(2, –1)

31. To
• dilate a figure with a scale factor of k
on the coordinate plane
• find the scale factor of a dilation of a
figure
Course 3, Lesson 6-4
Geometry

32. Symbols
• (x, y)  (kx, ky)
Course 3, Lesson 6-4
Geometry

33. Course 3, Lesson 6-4
Geometry
Words A dilation with a scale factor of k
will be:
• an enlargement, or an image
larger than the original, if k > 1,
• a reduction, or an image smaller
than the original, if 0 < k < 1,
• The same as the original figure
if k = 1
When the center of dilation in the coordinate plane is the
origin, each coordinate of the preimage is multiplied by the
scale factor k to find the coordinates of the image.
Symbols (x, y) → (kx, ky)

34. 1
Need Another Example?
2
3
Step-by-Step Example
1. A triangle has vertices A(0, 0), B(8, 0), and C(3, –2).
Find the coordinates of the triangle after a dilation
with a scale factor of 4.
The dilation is (x, y) → (4x, 4y). Multiply
the coordinates of each vertex by 4.
So, the coordinates after the dilation are
A'(0, 0), B'(32, 0), and C'(12, –8).
A(0, 0) → (4 • 0, 4 • 0) → (0, 0)
B(8, 0) → (4 • 8, 4 • 0) → (32, 0)
C(3, –2) → [4 • 3, 4 • (–2)] → (12, –8)

35. Answer
Need Another Example?
A triangle has vertices D(1, 2), E(0, 4), and
F(1, –1). Find the coordinates of the triangle
after a dilation with a scale factor of 3.
D'(3, 6), E'(0, 12), F'(3, –3)

36. 1
Need Another Example?
2
3
4
5
Step-by-Step Example
2. A figure has vertices J(3, 8), K(10, 6), and L(8, 2).
Graph the figure and the image of the figure after a dilation
with a scale factor of .
The dilation is (x, y) → x, y .
Multiply the coordinates of each
vertex by . Then graph both figures
on the coordinate plane.
Check
J(3, 8) → →
K(10, 6) → → K'(5, 3)
L(8, 2) → → L'(4, 1)
J
K
L
J'
K'
L'
Draw lines through the origin and each of the
vertices of the original figure. The vertices of
the dilation should lie on those same lines.

37. Answer
Need Another Example?
A figure has vertices H(–8, 4), J(6, 4), K(6, –4), and
L(–8, –4). Graph the figure and the image of the
figure after a dilation with a scale factor of .

38. 1
Need Another Example?
2
3
4
Step-by-Step Example
3. Through a microscope, the image of a grain of sand with a
0.25-millimeter diameter appears to have a diameter of
11.25 millimeters. What is the scale factor of the dilation?
Write a ratio comparing the diameters of the two images.
=
So, the scale factor of the dilation is 45.
= 45

39. Answer
Need Another Example?
The pupil of Josh’s eye is 6 millimeters in
diameter. His doctor uses medicine to dilate his
pupils so that they are 9 millimeters in diameter.
What is the scale factor of the dilation?