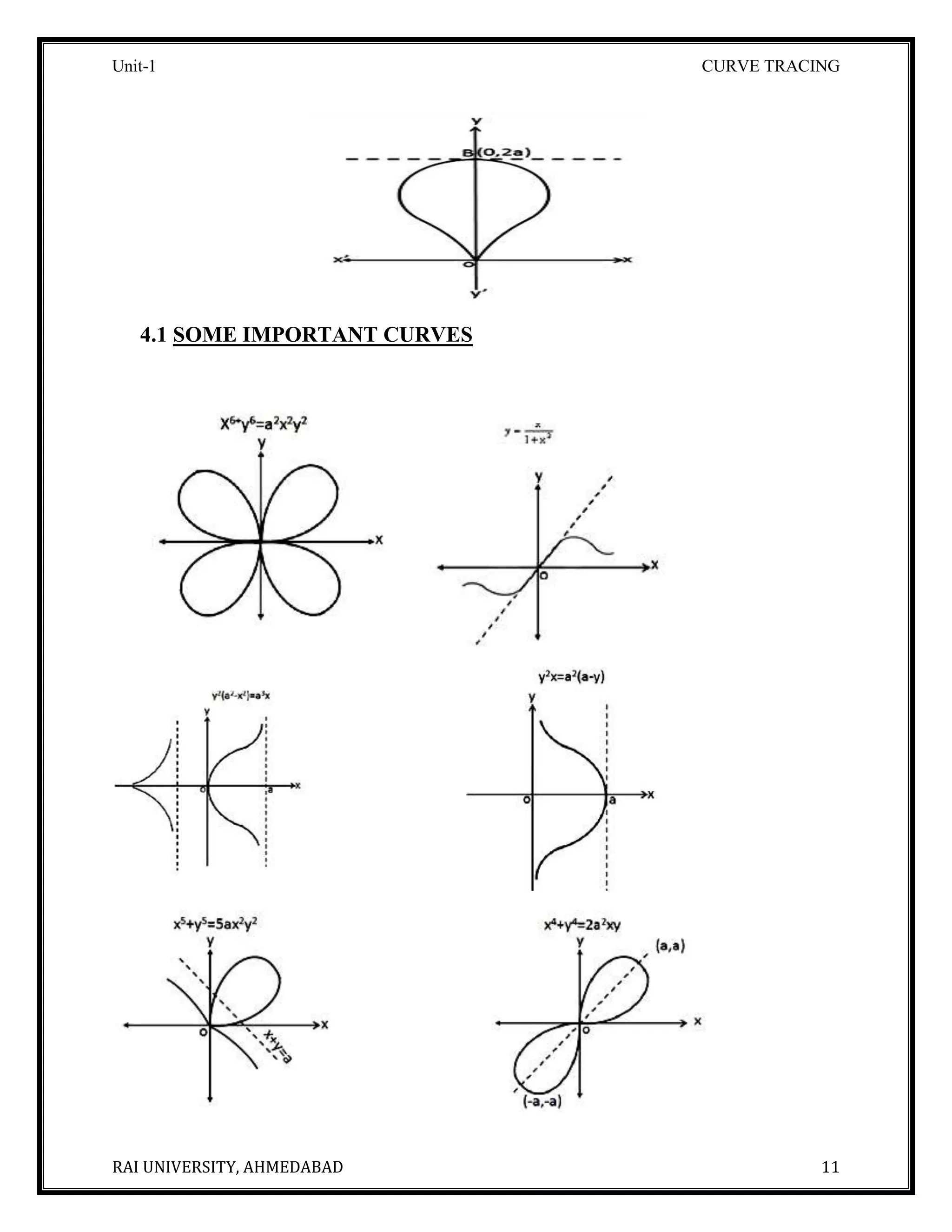
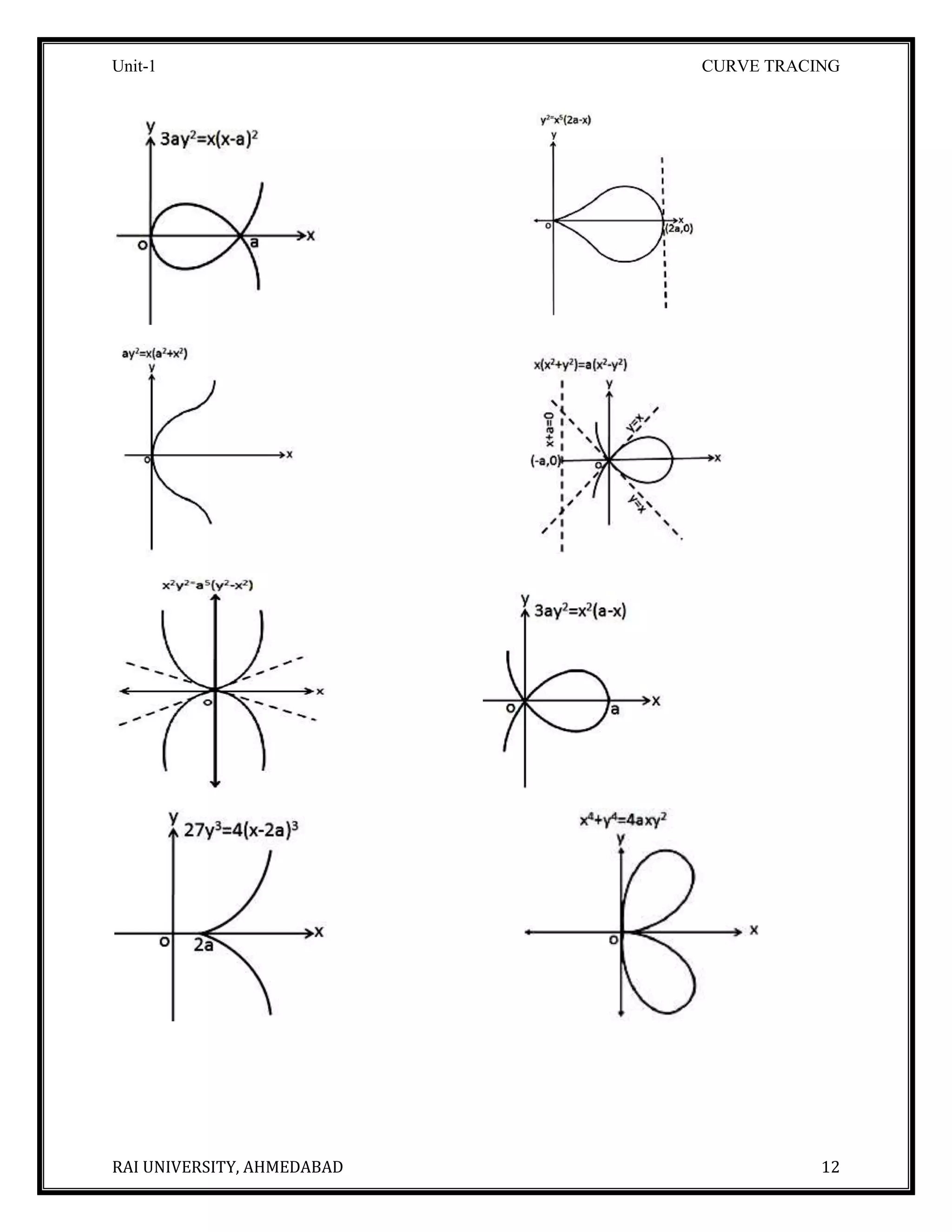
The document discusses curve tracing through Cartesian equations. It defines important concepts like singular points, multiple points, points of inflection, and asymptotes. It outlines the standard method of tracing a curve by examining its symmetry, intersection with axes, regions where the curve does not exist, and tangents. Several examples are provided to demonstrate how to apply this method to trace specific curves like cissoids, parabolas and hyperbolas.

1. Unit-1 CURVE TRACING
RAI UNIVERSITY, AHMEDABAD 1
Unit-I: CURVE TRACING
Sr. No. Name of the Topic Page No.
1 Important Definitions 2
2 Method of Tracing Curve 3
3 Examples 7
4 Some Important Curves 11
5 Exercise 13
6 Reference Book 13

2. Unit-1 CURVE TRACING
RAI UNIVERSITY, AHMEDABAD 2
CURVE TRACING
INTRODUCTION: The knowledge of curve tracing is to avoid the labour of
plotting a large number of points. It is helpful in finding the length of curve, area,
volume and surface area. The limits of integration can be easily found on tracing
the curve roughly.
1.1 IMPORTANT DEFINITIONS:
(I) Singular Points: This is an unusual point on a curve.
(II) Multiple points: A point through which a curve passes more than one
time.
(III) A double Point: If a curve passes two times through a point, then this
point is called a double point.
(a) Node: A double point at which two real tangents (not coincident) can
be drawn.
(b) Cusp: A double point is called cusp if the two tangents at it are
coincident.
(IV) Point of inflexion: A point where the curve crosses the tangent is called
a point of inflexion.
(V) Conjugate point: This is an isolated point. In its neighbour there is no
real point of the curve.
At each double point of the curve y=f(x), we get,
𝐷 = (
𝜕2 𝑓
𝜕𝑥𝜕𝑦
)
2
=
𝜕2 𝑓
𝜕𝑥2
×
𝜕2 𝑓
𝜕𝑦2

3. Unit-1 CURVE TRACING
RAI UNIVERSITY, AHMEDABAD 3
a) If D is +ve, double point is a node or conjugate point.
b) If D is 0, double point is a cusp or conjugate point.
c) If D is –ve, double point is a conjugate point.
2.1 METHOD OF TRACING A CURVE:
This method is used in Cartesian Equation.
1. Symmetry:
(a) A curve is symmetric about x-axis if the equation remains the same by
replacing y by –y. here y should have even powers only.
For ex: 𝑦2
=4ax.
(b)It is symmetric about y-axis if it contains only even powers of x.
For ex: 𝑥2
=4ay
(c) If on interchanging x and y, the equation remains the same then the curve
is symmetric about the line y=x.
For ex: 𝑥3
+ 𝑦3
= 3𝑎𝑥𝑦
(d)A curve is symmetric in the opposite quadrants if its equation remains the
same where x and y replaced by –x and –y respectively.
For ex: 𝑦 = 𝑥3
Symmetric about x-axis Symmetric about y-axis
Symmetric about a line y=x
2. (a) Curve through origin:
The curve passes through the origin, if the equation does not contain
constant term.

4. Unit-1 CURVE TRACING
RAI UNIVERSITY, AHMEDABAD 4
For ex: the curve 𝑦2
=4ax passes through the origin.
(b) Tangent at the origin:
To know the nature of a multiple point it is necessary to find the tangent at
that point.
The equation of the tangent at the origin can be obtained by equating to zero,
the lowest degree term in the equation of the curve.
3. The points of intersection with the axes:
(a) By putting y=0 in the equation of the curve we get the co-ordinates of the
point of intersection with the x-axis.
For ex:
𝑥2
𝑎2
+
𝑦2
𝑏2
= 1 put y=0 we get 𝑥 = ±𝑎
Thus, (a, 0) and (-a, 0) are the co-ordinates of point of intersection.
(b)By putting x=0 in the equation of the curve, the co-ordinate of the point
of intersection with the y-axis is obtained by solving the new equation.
4. Regions in which the curve does not lie:
If the value of y is imaginary for certain value of x then the curve does not
exist for such values.
Example 1: 𝑦2
= 4𝑥
Answer: For negative value of x, if y is imaginary then there is no curve in
second and third quadrants.
Example 2: 𝑎2
𝑥2
= 𝑦3(2𝑎 − 𝑦).
Answer: (i) For y>2a, x is imaginary. There is no curve beyond y=2a.
(ii) For negative value of y, if x is imaginary then there is no curve
in 3rd
and 4th
quadrants.
5. Asymptotes are the tangents to the curve at infinity:
(a)Asymptote parallel to the x-axis is obtained by equating to zero, the
coefficient of the highest power of x.
For ex: 𝑦𝑥2
− 4𝑥2
+ 𝑥 + 2 = 0
 (𝑦 − 4)𝑥2
+ 𝑥 + 2 = 0

5. Unit-1 CURVE TRACING
RAI UNIVERSITY, AHMEDABAD 5
The coefficient of the highest power of x 𝑖. 𝑒 𝑥2
is 𝑦 − 4 = 0
∴ 𝑦 − 4 = 0 is the asymptote parallel to the x-axis.
(b) Asymptote parallel to the y-axis is obtained by equating to zero, the
coefficient of highest power of y.
For ex: 𝑥𝑦3
− 2𝑦3
+ 𝑦2
+ 𝑥2
+ 2 = 0
 (𝑥 − 2)𝑦3
+ 𝑦2
+ 𝑥2
+ 2 = 0
The coefficient of the highest power of 𝑦 𝒊. 𝒆. 𝑦3
is 𝑥 − 2.
∴ 𝑥 − 2 = 0 is the asymptote parallel to y-axis.
(c) Oblique Asymptote: 𝒚 = 𝒎𝒙 + 𝒄
(I) Find ∅ 𝑛(𝑚) by putting x=1 and y=m in highest degree (n) terms of
the equation of the curve.
(II) Solve ∅ 𝑛(𝑚) = 0 for 𝑚
(III) Find ∅ 𝑛−1(𝑚) by putting x=1 and y=m in the next highest degree
(n-1) terms of the equation of the curve.
(IV) Find 𝑐 by the formula, 𝑐 = −
∅ 𝑛−1(𝑚)
∅′
𝑛(𝑚)
, if the values of m are not
equal, then find 𝑐 by
𝑐2
2
∅′′
𝑛(𝑚) + 𝑐∅′
𝑛−1(𝑚) + ∅ 𝑛−2(𝑚) = 0
(V) Obtain the equation of asymptote by putting the values of m and c in
𝑦 = 𝑚𝑥 + 𝑐.
For ex: Find asymptote of 𝑥3
+ 𝑦3
− 3𝑥𝑦 = 0
Solution: Here, ∅3(𝑚) = 1 + 𝑚3
and ∅2(𝑚) = −3𝑚
Putting ∅3(𝑚) = 0 or 𝑚3
+ 1 = 0
 (𝑚 + 1)(𝑚2
− 𝑚 + 1) = 0
 𝑚 = −1, 𝑚 =
1±√1−4
2
 Only real value of m is −1.
Now we find c from the equation

6. Unit-1 CURVE TRACING
RAI UNIVERSITY, AHMEDABAD 6
𝑐 = −
∅ 𝑛−1(𝑚)
∅′
𝑛(𝑚)
𝑐 = −
−3𝑚
3𝑚2
=
1
𝑚
=
1
−1
= −1
On putting 𝑚 = −1 and 𝑐 = −1 in 𝑦 = 𝑚𝑥 + 𝑐, the equation of
asymptote is
𝑦 = (−1)𝑥 + (−1)
 𝑥 + 𝑦 + 1 = 0
6. Tangent:
Put
𝑑𝑦
𝑑𝑥
= 0 for the points where tangent is parallel to the x-axis.
For ex: 𝑥2
+ 𝑦2
− 4𝑥 + 4𝑦 − 1 = 0
 2𝑥 + 2𝑦
𝑑𝑦
𝑑𝑥
− 4 + 4
𝑑𝑦
𝑑𝑥
= 0
 (2𝑦 + 4)
𝑑𝑦
𝑑𝑥
= 4 − 2𝑥

𝑑𝑦
𝑑𝑥
=
4−2𝑥
2𝑦+4
Now,
𝑑𝑦
𝑑𝑥
= 0
4 − 2𝑥 = 0.
 𝑥 = 2
Putting 𝑥 = 2 in (i), we get 𝑦2
+ 4𝑦 − 5 = 0
∴ 𝑦 = 1, −5
The tangents are parallel to x-axis at the points (2,1) and (2,-5).
7. Table:
Prepare a table foe certain values of x and y and draw the curve passing
through them.

7. Unit-1 CURVE TRACING
RAI UNIVERSITY, AHMEDABAD 7
For Ex: 𝑦2
= 4𝑥 + 4
X -1 0 1 2 3
y 0 ±2 ±2√2 ±2√3 ±4
Note : Remember POSTER. Where,
P = point of intersection
O = Origin
S = Symmetry
T = Tangent
A = Asymptote
R = Region
3.1 Trace the following curves:
Example 1: Trace the curve 𝑎𝑦2
= 𝑥2
(𝑎 − 𝑥)
Solution: we have,
𝑎𝑦2
= 𝑥2
(𝑎 − 𝑥) ________ (i)
1) Symmetry: Since the equation (i) contains only even power of y,
∴ it is symmetric about the x-axis.
It is not symmetric about y-axis since it does not contain even power
of x.
2) Origin: Since constant term is absent in (i), it passes through origin.
3) Intersection with x-axis:
Putting y=0 in (i), we get x=a.
∴ Curve cuts the x-axis at (a, 0).
4) Tangent: The equation of the tangent at origin is obtained by
equating to zero the lowest degree term of the equation (i).
𝑎𝑦2
= 𝑎𝑥2
.

8. Unit-1 CURVE TRACING
RAI UNIVERSITY, AHMEDABAD 8
 𝑦2
= 𝑥2
 𝑦 = ±𝑥
There are two tangents 𝑦 = ±𝑥 at the origin to the given curve.
Example 2: Trace 𝑦2(𝑎2
+ 𝑥2) = 𝑥2(𝑎2
− 𝑥2)
Solution: Here we have,
𝑦2(𝑎2
+ 𝑥2) = 𝑥2(𝑎2
− 𝑥2) _____________(i)
1) Origin: The equation of the given curve does not contain constant
term, therefore, the curve passes through origin.
2) Symmetric about axes: The equation contains even powers of x as
well as y, so the curve is symmetric about both the axes.
3) Point of intersection with x-axis: On putting y=0 in the equation,
we get
𝑥2(𝑎2
− 𝑥2) = 0, 𝑥 = ±𝑎, 0,0
4) Tangent at the origin: Equation of the tangent is obtained by
equating to zero the lowest degree term.
𝑎2
𝑦2
− 𝑎2
𝑥2
= 0 ⇒ 𝑦 = ±𝑥
There are two tangents 𝑦 = 𝑥 and 𝑦 = −𝑥 at the origin.
5) Node: Origin is the node, since, there are two real and different
tangents at the origin.
6) Region of absence of the curve: For values of 𝑥 > 𝑎 and 𝑥 < −𝑎,
𝑦2
becomes negative, hence, the entire curve remains between 𝑥 =
−𝑎 𝑎𝑛𝑑 𝑥 = 𝑎.

9. Unit-1 CURVE TRACING
RAI UNIVERSITY, AHMEDABAD 9
Example 3: Trace the curve 𝑦2(2𝑎 − 𝑥) = 𝑥3
(cissoid)
Solution: We have, 𝑦2
=
𝑥3
(2𝑎−𝑥)
_____________ (i)
1) Origin: Equation does not contain any constant term. Therefore, it passes
through origin.
2) Symmetric about x-axis: Equation contains only even powers of y,
therefore, it is symmetric about x-axis.
3) Tangent at the origin: Equation of the tangent is obtained by equating to
zero the lowest degree terms in the equation (i).
2𝑎𝑦2
− 𝑥𝑦2
= 𝑥3
Equation of tangent:
2𝑎𝑦2
= 0 ⟹ 𝑦2
= 0, 𝑦 = 0 is the double point.
4) Cusp: As two tangents are coincident, therefore, origin is a cusp.
5) Asymptote parallel to y-axis: Equation of asymptote is obtained by
equating the coefficient of highest degree of y to zero.
2𝑎𝑦2
− 𝑥𝑦2
= 𝑥3
⟹ (2𝑎 − 𝑥)𝑦2
= 𝑥3
 Equation of asymptote is 2𝑎 − 𝑥 = 0 ⟹ 𝑥 = 2𝑎.
6) Region of absence of curve: 𝑦2
becomes negative on putting
𝑥 > 2𝑎 𝑜𝑟 𝑥 < 0, therefore, the curve does not exist for
𝑥 < 0 𝑎𝑛𝑑 𝑥 > 2𝑎 .

10. Unit-1 CURVE TRACING
RAI UNIVERSITY, AHMEDABAD 10
Example 4: Trace the curve 𝑎2
𝑥2
= 𝑦2
(2𝑎 − 𝑦)
Solution: we have, 𝑎2
𝑥2
= 𝑦2
(2𝑎 − 𝑦) _________(i)
1) Symmetry:
(a) The curve is symmetric about y-axis. Since all the powers of x are even.
(b) Not symmetric about x-axis. Since all the powers of y are not even.
2) Origin: The curve passes through the origin since the equation does not
contain any constant term.
3) Region of absence of the curve: If y is greater than 2a the right hand side
becomes negative but left hand side becomes positive hence, the curve does
not exist when y=2.
4) Tangent at the origin: On putting the lowest degree term to zero 𝑎2
𝑥2
=
𝑦2
2𝑎 ⟹ 𝑎𝑥2
= 2𝑦2
⟹ 𝑦 = ±√
𝑎
2
𝑥
5) Intercept on y-axis: On putting x=0 in the equation, we get
⟹ 0 = 𝑦2
(2𝑎 − 𝑦)
⟹ 2𝑎 − 𝑦 = 0
⟹ 𝑦 = 2𝑎

11. Unit-1 CURVE TRACING
RAI UNIVERSITY, AHMEDABAD 11
4.1 SOME IMPORTANT CURVES

12. Unit-1 CURVE TRACING
RAI UNIVERSITY, AHMEDABAD 12

13. Unit-1 CURVE TRACING
RAI UNIVERSITY, AHMEDABAD 13
5.1 EXERCISE:
Trace the following curves.
1) 𝑥𝑦2
= 4𝑎2
(2𝑎 − 𝑥)
2) 𝑦2
(4 − 𝑥) = 𝑥3
3) 𝑥5
+ 𝑦5
= 5𝑎𝑥2
𝑦2
4) 3𝑎𝑦2
= 𝑥(𝑥 − 𝑎2
)
6.1 REFERENCE BOOK:
1) Introduction to Engineering Mathematics
By H. K. DASS. & Dr. RAMA VERMA
2) WWW.brightclasses.in
3) www.sakshieducation.com/.../M1...EnvelopesCurveTracing.pdf
4) Higher Engineering Mathematics
By B.V.RAMANA