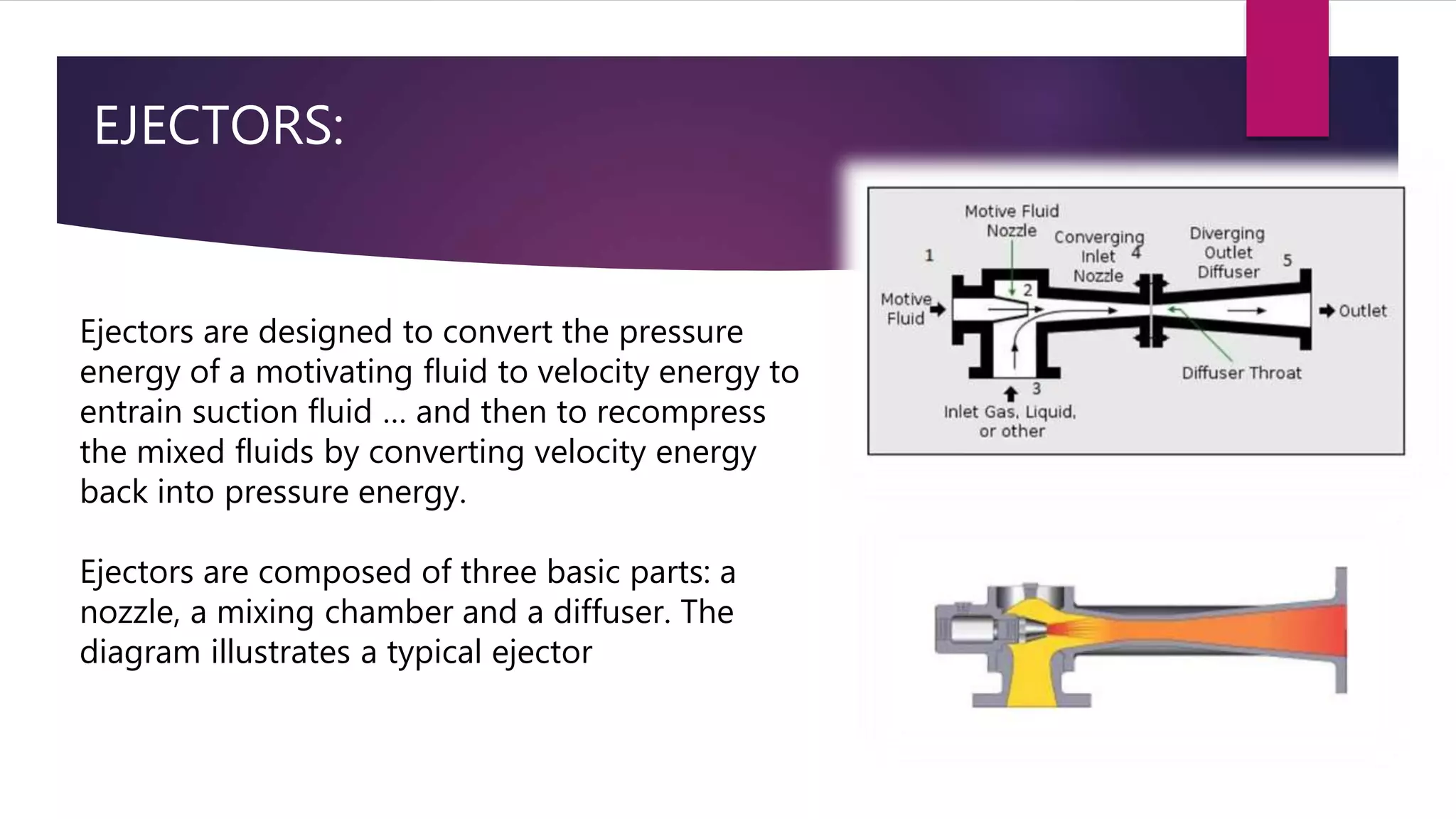
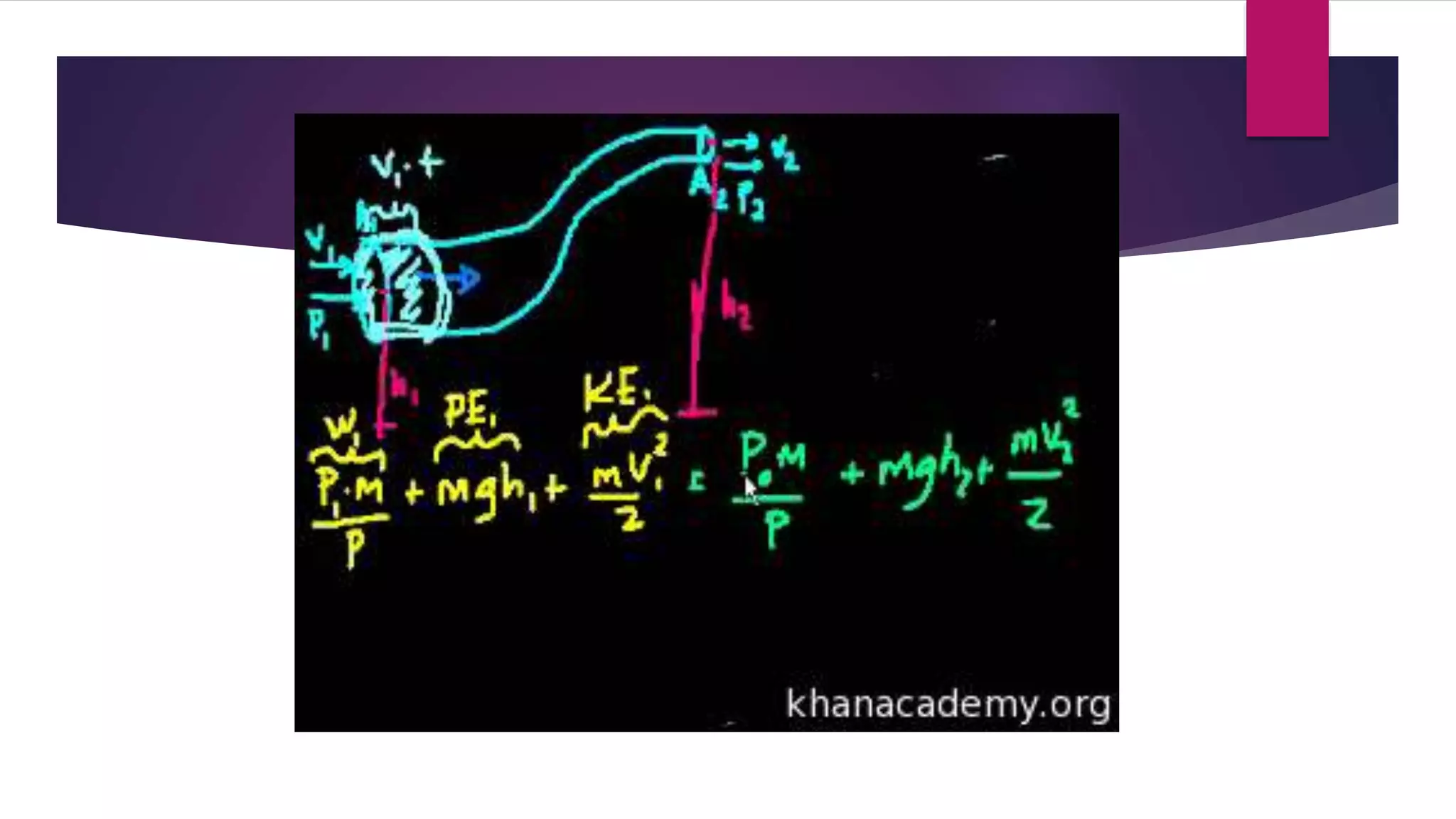
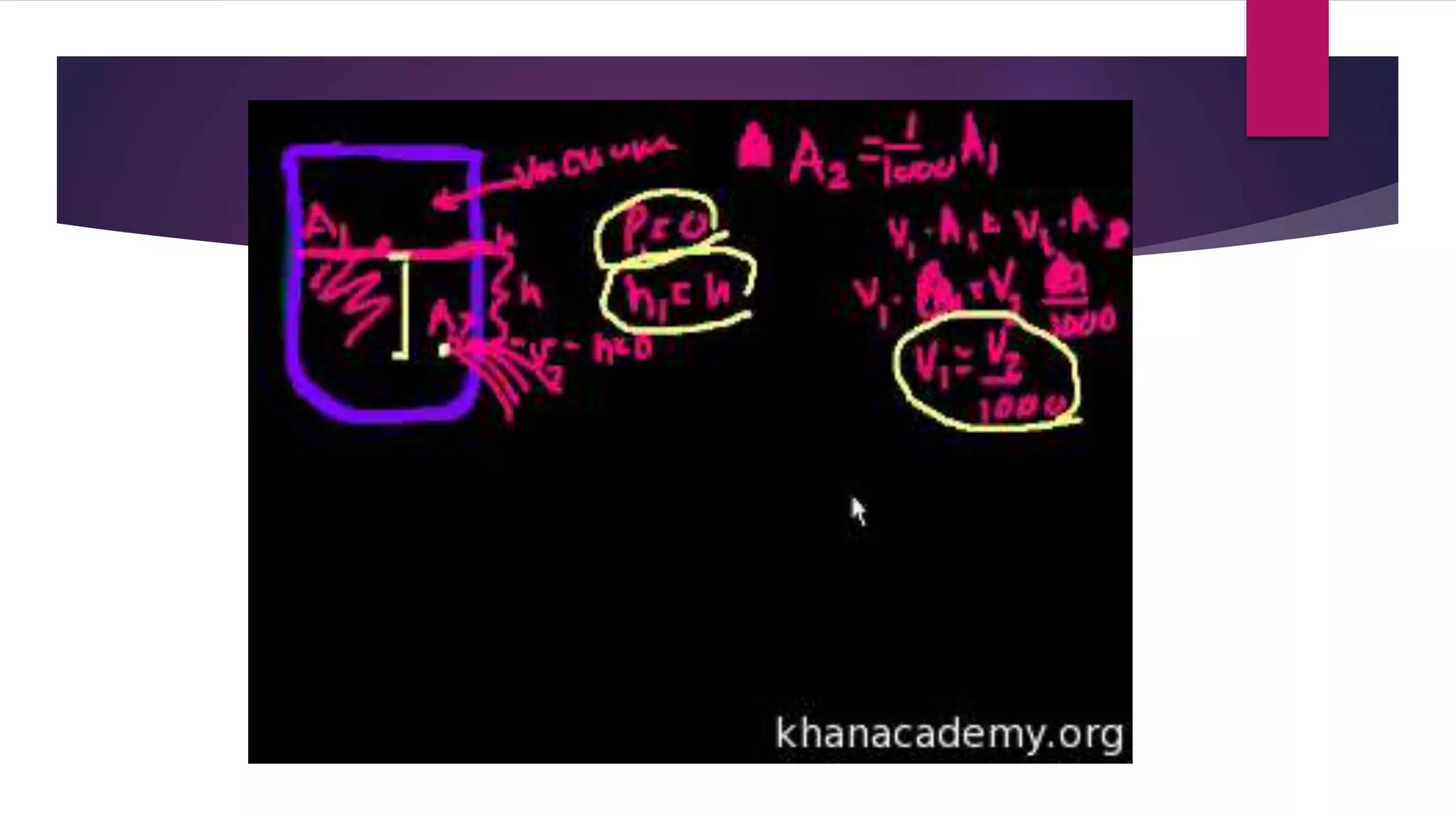
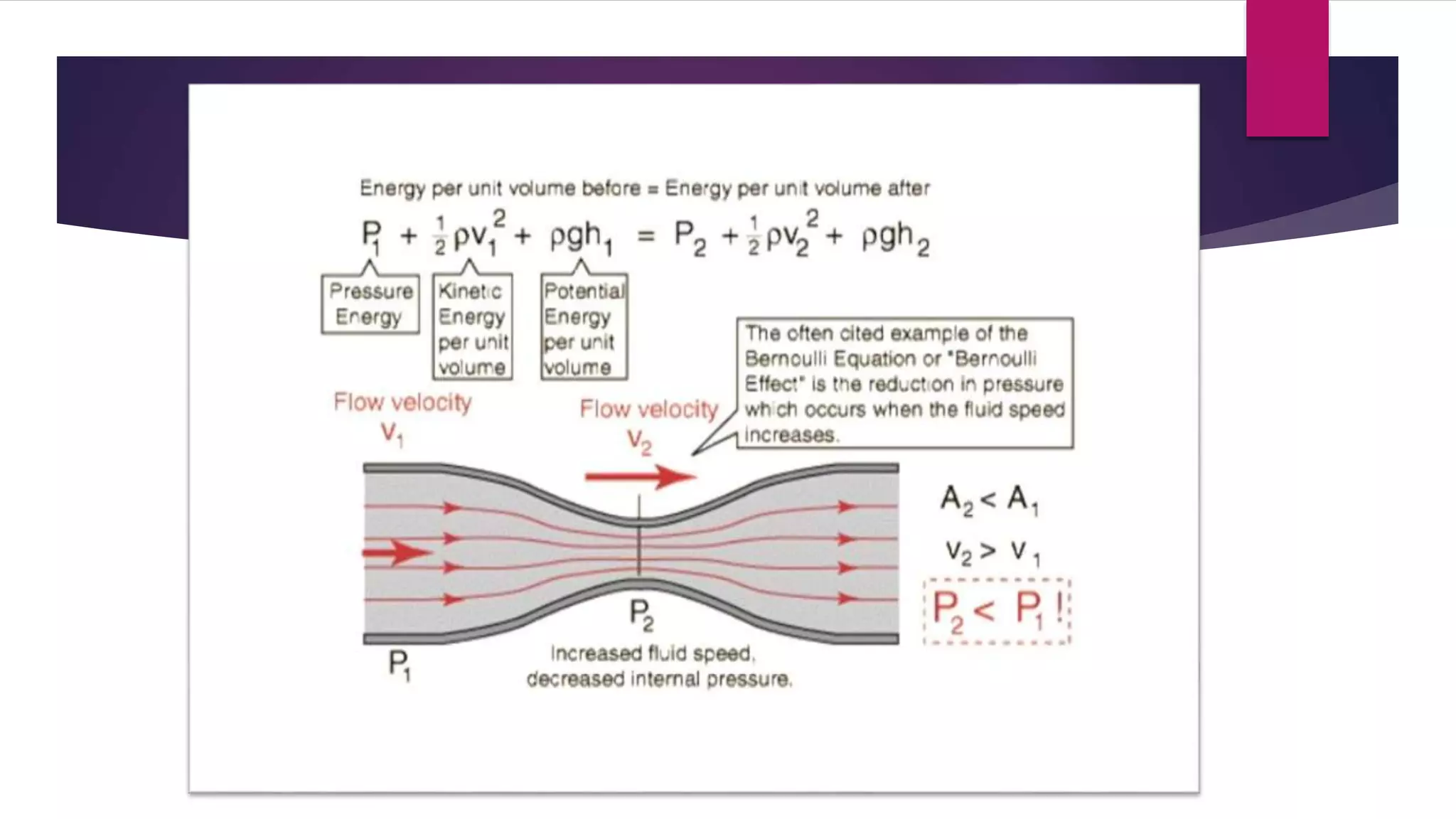
Bernoulli's theorem, established by Swiss physicist Daniel Bernoulli in 1738, describes the relationship between fluid velocity and pressure, stating that an increase in fluid speed leads to a decrease in pressure. This principle is fundamental in various applications, including calculating lift forces on airfoils, carburetor function, and pressure measurements with devices like pitot tubes. Bernoulli's equation emphasizes the conservation of energy in fluid dynamics, where the combined pressure, kinetic, and potential energies remain constant along a streamline.

1. BERNOULLI’S THEOREM
MADE BY-
GAURAV YADAV
XI –A
10

2. BERNOULLI’S THEOREM
 Daniel Bernoulli
Swiss physicist (1700–1782)
Bernoulli made important discoveries
in fluid dynamics. Bernoulli’s most
famous work, Hydrodynamica, was
published in 1738; it is both a theoretical and a
practical study of equilibrium,
pressure, and speed in fluids. He showed
that as the speed of a fluid increases,
its pressure decreases. Referred to as
“Bernoulli’s principle,” Bernoulli’s work
is used to produce a partial vacuum in
chemical laboratories by connecting a
vessel to a tube through which water is
running rapidly.

3. INTRODUCTION
 In fluid dynamics, Bernoulli's principle states that for
an inviscid flow of a non-conducting fluid, an
increase in the speed of the fluid occurs
simultaneously with a decrease in pressure or a
decrease in the fluid's potential energy.The principle
is named after Daniel Bernoulli who published it in
his book Hydrodynamica in 1738.[3]

4. BERNOLLI’S EQUATION
 Consider an element of fluid with uniform density. The change in energy of that
element as it moves along a pipe must be zero - conservation of energy. This is
the basis for Bern
 For any point along a flow tube or streamline
p + 1
2ρ𝑣2
+ ρ g y = constant
 Between any two points along a flow tube or streamline

6. DIMENSIONS

7. DERIVATION

10. ENERGY FORM:
𝑃2
𝜌
+
𝑉2
2
2
+ g𝑧2 =
𝑃1
𝜌
+
𝑉1
2
2
+ g 𝑧1
Pressure energy + Kinetic energy + potential energy = constant
HEAD FORM:
P2
ρg
+
V2
2
2g
+ z2 =
P1
ρg
+
V1
2
2g
+ z1
Pressure head + kinetic head + potential head = constant
PRESSURE FORM:
𝑃2+ 𝜌
𝑉2
2
2
+ 𝜌g𝑧2 =𝑃1+ 𝜌𝑉1
2
2
+ 𝜌g 𝑧1
Static pressure + dynamic pressure + hydrostatic pressure = constant

11. APPLICATIONS
 In modern everyday life there are many observations that can be successfully explained by
application of Bernoulli's principle, even though no real fluid is entirely inviscid[25] and a small
viscosity often has a large effect on the flow.
 Bernoulli's principle can be used to calculate the lift force on an airfoil, if the behaviour of the fluid
flow in the vicinity of the foil is known. For example, if the air flowing past the top surface of an
aircraft wing is moving faster than the air flowing past the bottom surface, then Bernoulli's
principle implies that the pressure on the surfaces of the wing will be lower above than below. This
pressure difference results in an upwards lifting force.[26][27] Whenever the distribution of speed
past the top and bottom surfaces of a wing is known, the lift forces can be calculated (to a good
approximation) using Bernoulli's equations[28] – established by Bernoulli over a century before the
first man-made wings were used for the purpose of flight. Bernoulli's principle does not explain
why the air flows faster past the top of the wing and slower past the underside. See the article on
aerodynamic lift for more info.

12.  The carburetor used in many reciprocating engines contains a venturi to create a region of low pressure to
draw fuel into the carburetor and mix it thoroughly with the incoming air. The low pressure in the throat of a
venturi can be explained by Bernoulli's principle; in the narrow throat, the air is moving at its fastest speed
and therefore it is at its lowest pressure.
 The pitot tube and static port on an aircraft are used to determine the airspeed of the aircraft. These two
devices are connected to the airspeed indicator, which determines the dynamic pressure of the airflow past
the aircraft. Dynamic pressure is the difference between stagnation pressure and static pressure. Bernoulli's
principle is used to calibrate the airspeed indicator so that it displays the indicated airspeed appropriate to
the dynamic pressure.[29]
 The flow speed of a fluid can be measured using a device such as a Venturi meter or an orifice plate, which
can be placed into a pipeline to reduce the diameter of the flow. For a horizontal device, the continuity
equation shows that for an incompressible fluid, the reduction in diameter will cause an increase in the fluid
flow speed. Subsequently Bernoulli's principle then shows that there must be a decrease in the pressure in
the reduced diameter region. This phenomenon is known as the Venturi effect.
 The maximum possible drain rate for a tank with a hole or tap at the base can be calculated directly from
Bernoulli's equation, and is found to be proportional to the square root of the height of the fluid in the tank.
This is Torricelli's law, showing that Torricelli's law is compatible with Bernoulli's principle. Viscosity lowers
this drain rate. This is reflected in the discharge coefficient, which is a function of the Reynolds number and
the shape of the orifice.[30]
 The Bernoulli grip relies on this principle to create a non-contact adhesive force between a surface and the
gripper.

13. Condensation visible over
the upper surface of
an Airbus A340 wing caused
by the fall in temperature
accompanying the fall in
pressure, both due to
acceleration of the air.

14. APPLICATION IN PUMPS:
Volute in the casing of centrifugal pumps
converts velocity of fluid into pressure energy
by increasing area of flow.
The conversion of kinetic energy into pressure
is according to the Bernoulli equation.

15. SIZING OF PUMPS:
𝑃2
𝜌
+
𝑉2
2
2
+ g𝑧2 =
𝑃1
𝜌
+
𝑉1
2
2
+ g 𝑧1 − 𝑙𝑜𝑠𝑠𝑒𝑠 − 𝑤𝑠
−𝑤𝑠 = 𝑙𝑜𝑠𝑠 +
𝑉2
2
2
+ 𝑔(𝑧2 + 𝑧1)

16. EJECTORS:
Ejectors are designed to convert the pressure
energy of a motivating fluid to velocity energy to
entrain suction fluid … and then to recompress
the mixed fluids by converting velocity energy
back into pressure energy.
Ejectors are composed of three basic parts: a
nozzle, a mixing chamber and a diffuser. The
diagram illustrates a typical ejector

17. PITOT TUBE
Pitot tube is a pressure measurement instrument
Used to measure fluid flow velocity.
Pitot tubes can be used to indicate fluid flow
velocity by measuring the difference between the
static and dynamic pressures in fluids.
The principle is based on the Bernoulli Equation.
𝑃2+
𝜌𝑉2
2
2
+ g𝜌𝑧2 = 𝑃1+
𝜌𝑉1
2
2
+ gρ 𝑧1
𝑃2= 𝑃1+
𝜌𝑉1
2
2
𝑉1 =
2(𝑃𝑡 − 𝑃𝑠)
𝜌

18. CARBURETOR:
The carburetor works on Bernoulli principle: the
faster air moves, the lower its static pressure, and
the higher its dynamic pressure.
The throttle (accelerator) linkage does not directly
control the flow of liquid fuel. Instead, it actuates
carburetor mechanisms which meter the flow of air
being pulled into the engine. The speed of this flow,
and therefore its pressure, determines the amount
of fuel drawn into the airstream.

19. SIPHON
Siphon, a bent tube used to move a liquid over an obstruction to a
lower level without pumping. A siphon is most commonly used to
remove a liquid from its container. The siphon tube is bent over the
edge of the container, one end in the liquid and the other outside
end at a lower level than the surface of the liquid in the container.
Static pressure + dynamic pressure + hydrostatic pressure=constant
𝑷 𝟐
𝝆
+
𝑽 𝟐
𝟐
𝟐
+ g𝒛 𝟐 =
𝑷 𝟏
𝝆
+
𝑽 𝟏
𝟐
𝟐
+ g𝒛 𝟏
𝟎 +
𝑽 𝟐
𝟐
𝟐
+0 = 0+ 0+ gH
𝑽 𝟐 = 𝟐𝒈𝑯

20. VIDEO Lecture

25. NUMERICAL
 Problem # 1:
 Water at a gauge pressure of 3.8 atm at street level flows in to an office building at a speed of 0.06 m/s through a pipe 5.0 cm
in diameter. The pipes taper down to 2.6cm in diameter by the top floor, 20 m above. Calculate the flow velocity and the
gauge pressure in such a pipe on the top floor. Assume no branch pipe and ignore viscosity.
Solution:
By continuity equation:
v2 = (A1v1) / A2 = (π (5.0 / 2)2 (0.60) ) / ( π (2.6 / 2)2)
v2 = 2.2 m/s
By Bernoulli’s Equation:
P1 + ρgh1 + ½ρ(v1)2 = P2 + ρgh2 + ½ρ(v2)2 (Po = atmospheric pressure)
P2 = (3.8 x Po) + Po + ½(1000)(0.6)2 – (1000)(9.8)(20) – (1000)½(2.2)2
P2 = 2.8 x 105 Pa

26.  #2 Problem
 The diameter of a pipe changes from 200mm at a
section 5m above datum to 50mm at a section 3m
above datum. The pressure of water at first section is
500kPa. If the velocity of the flow at the first section
is 1m/s, determine the intensity of pressure at the
second section.

27. Given,
Let,
• = Velocity of flow at section (2), and
• = Pressure at section (2).
We know that area of the pipe at section (1),